Early dinosaurs showed rapid evolutionary rates, which were sustained on the line leading to birds. Maintenance of evolvability in key lineages might explain the uneven distribution of trait diversity among groups of animal species.
Abstract
Large-scale adaptive radiations might explain the runaway success of a minority of extant vertebrate clades. This hypothesis predicts, among other things, rapid rates of morphological evolution during the early history of major groups, as lineages invade disparate ecological niches. However, few studies of adaptive radiation have included deep time data, so the links between extant diversity and major extinct radiations are unclear. The intensively studied Mesozoic dinosaur record provides a model system for such investigation, representing an ecologically diverse group that dominated terrestrial ecosystems for 170 million years. Furthermore, with 10,000 species, extant dinosaurs (birds) are the most speciose living tetrapod clade. We assembled composite trees of 614–622 Mesozoic dinosaurs/birds, and a comprehensive body mass dataset using the scaling relationship of limb bone robustness. Maximum-likelihood modelling and the node height test reveal rapid evolutionary rates and a predominance of rapid shifts among size classes in early (Triassic) dinosaurs. This indicates an early burst niche-filling pattern and contrasts with previous studies that favoured gradualistic rates. Subsequently, rates declined in most lineages, which rarely exploited new ecological niches. However, feathered maniraptoran dinosaurs (including Mesozoic birds) sustained rapid evolution from at least the Middle Jurassic, suggesting that these taxa evaded the effects of niche saturation. This indicates that a long evolutionary history of continuing ecological innovation paved the way for a second great radiation of dinosaurs, in birds. We therefore demonstrate links between the predominantly extinct deep time adaptive radiation of non-avian dinosaurs and the phenomenal diversification of birds, via continuing rapid rates of evolution along the phylogenetic stem lineage. This raises the possibility that the uneven distribution of biodiversity results not just from large-scale extrapolation of the process of adaptive radiation in a few extant clades, but also from the maintenance of evolvability on vast time scales across the history of life, in key lineages.
Author Summary
Animals display huge morphological and ecological diversity. One possible explanation of how this diversity evolved is the "niche filling" model of adaptive radiation—under which evolutionary rates are highest early in the evolution of a group, as lineages diversify to fill disparate ecological niches. We studied patterns of body size evolution in dinosaurs and birds to test this model, and to explore the links between modern day diversity and major extinct radiations. We found rapid evolutionary rates in early dinosaur evolution, beginning more than 200 million years ago, as dinosaur body sizes diversified rapidly to fill new ecological niches, including herbivory. High rates were maintained only on the evolutionary line leading to birds, which continued to produce new ecological diversity not seen in other dinosaurs. Small body size might have been key to maintaining evolutionary potential (evolvability) in birds, which broke the lower body size limit of about 1 kg seen in other dinosaurs. Our results suggest that the maintenance of evolvability in only some lineages explains the unbalanced distribution of morphological and ecological diversity seen among groups of animals, both extinct and extant. Important living groups such as birds might therefore result from sustained, rapid evolutionary rates over timescales of hundreds of millions of years.
Introduction
Much of extant biodiversity may have arisen from a small number of adaptive radiations occurring on large spatiotemporal scales [1]–[3]. Under the niche-filling model of adaptive radiation, ecological opportunities arise from key innovations, the extinction of competitors, or geographic dispersal [1],[4],[5]. These cause rapid evolutionary rates in ecologically relevant traits, as diverging lineages exploit distinct resources. Rates of trait evolution then decelerate as niches become saturated, a pattern that has been formalised as the “early burst” model (e.g., [6],[7]).
Most phylogenetic studies of adaptive radiations focus on small scales such as island radiations and other recently diverging clades, including Anolis lizards, cichlid fishes, and geospizine finches [2],[6],[8]–[10]. Detailed study of these model systems has demonstrated the importance of ecological and functional divergence as drivers of speciation early in adaptive radiations (e.g., [11],[12]). Surprisingly though, early burst patterns of trait evolution receive only limited support from model comparison approaches for these and other adaptive radiations occurring in geographically restricted areas and on short timescales (<50 million years [Ma]; most <10 Ma) [6] (but see [13],[14]).
Studies of morphological evolution on longer timescales, unfolding over 100 Ma or more, are central to establishing whether niche-filling or early burst patterns of trait evolution are important evolutionary phenomena on large phylogenetic scales. A small number of recent studies quantified patterns of trait evolution on large scales using neontological phylogenies. For example, diversification rates and morphological rates are positively correlated in actinopterygians [15] (∼400 Ma); rapid rates of both morphological and molecular evolution occur on deep, Cambrian, nodes of the arthropod tree of life [16] (∼540 Ma); and the early evolution of placental mammals was characterised by rapid rates of diversification [17] (100–65 Ma) and perhaps body size evolution [18] (but see [19]).
However, even the largest neontological studies [15]–[18],[20],[21] are limited to explaining the rise of important extant groups. A more complete characterisation of macroevolutionary processes on long timescales should also explain the ascent and demise of important extinct groups (e.g., [22]), which in fact represent most of life's diversity. Substantial evidence for the dynamics of past adaptive radiations might have been erased from the neontological archive, and macroevolutionary models for extinct or declining/depauperate clades may be tested most effectively using deep time data from the fossil record [23],[24].
Palaeontologists often quantify patterns of morphological radiation using time series of disparity (e.g., [25],[26]). However, few phylogenetic studies including fossil data have attempted to explain patterns of morphological radiation in large clades on timescales >100 Ma, and most have individually targeted either the roots of exceptional modern clades such as birds or mammals (e.g., [19],[27],[28]) or extinct/depauperate clades (e.g., [29]–[31]; studies based on discrete characters). Thus, patterns of morphological evolution in major extinct clades, and their links to successful modern clades, are not well understood.
Non-avian dinosaurs are an iconic group of terrestrial animals. They were abundant and ecologically diverse for most of the Mesozoic, and included extremely large-bodied taxa that challenge our understanding of size limits in terrestrial animals [32]. The first dinosaurs appeared more than 230 Ma ago in the Triassic Period, as small-bodied (10–60 kg), bipedal, generalists. By the Early Jurassic (circa 200 Ma), they dominated terrestrial ecosystems in terms of species richness [33],[34], and Cretaceous dinosaurs (145–66 Ma) had body masses spanning more than seven orders of magnitude (Figure 1A). Non-avian dinosaurs became extinct at the catastrophic Cretaceous/Paleogene (K/Pg) boundary event, at or near the peak of their diversity [35],[36]. In contrast, extant dinosaurs (neornithine birds) comprise around 10,000 species and result from one of the most important large-scale adaptive radiations of the Cenozoic [3],[21].
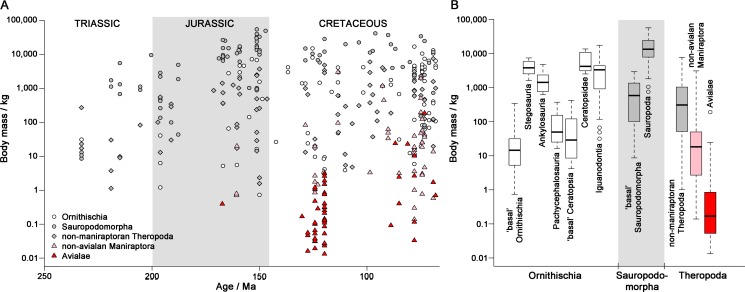
Figure 1. Dinosaur body masses.
(A) Dinosaur body mass through time (the full set of mass estimates is given in Dataset S1). (B) Box-and-whisker plot showing median (dark line), hinges (box range), and ranges (whiskers) of body masses for major dinosaur groups. Outliers (circles) include the iguanodontians Mochlodon vorosi (31 kg), Elrhazosaurus, and Valdosaurus (both 48 kg), the sauropods Europasaurus (1,050 kg) and Magyarosaurus (746 kg), and the flightless avialan Gargantuavis (180 kg).
The proposed drivers of early dinosaur diversification are controversial. Although various causal factors have been suggested to underlie a presumed adaptive radiation, few studies have tested the predictions of niche-filling models, and these have yielded equivocal results. An upright, bipedal gait, rapid growth, and possible endothermy have been proposed as key innovations of Triassic dinosaurs (reviewed by [34]), and mass extinctions during the Triassic/Jurassic boundary interval removed competing clades, perhaps leading to ecological release and rapid rates of body size evolution in Early Jurassic dinosaurs [37] (but see [34]). However, quantitative studies using body size proxies [34] and discrete morphological characters [33] have found only weak support for the niche-filling model during early dinosaur evolution, instead favouring gradualistic evolutionary rates. These studies focussed on the Late Triassic–Early Jurassic, so it is unclear whether Early Jurassic dinosaur evolution differed from later intervals (consistent with radiation following a mass extinction), or how the Middle Jurassic–Cretaceous radiation of birds and their proximate relatives relates to overall patterns of dinosaur diversification.
We used phylogenetic comparative methods [6],[14],[38],[39] to analyse rates of dinosaur body mass evolution ( Materials and Methods ; Appendix S1). For this study, we compiled a large dataset of dinosaur body masses (441 taxa; Dataset S1) using the accurate scaling relationship of limb robustness (shaft circumference) derived from extant tetrapods [40] (Appendix S1; Dataset S1). Body mass affects all aspects of organismal biology and ecology (e.g., [41],[42]), including that of dinosaurs (e.g., [43]–[45]). Because of its relationship with animal energetics and first-order ecology, understanding the evolution of body mass is fundamental to identifying the macroevolutionary processes underlying biodiversity seen in both ancient and modern biotas. Therefore, by studying body mass evolution, we assess the broad pattern of niche filling in the assembly of dinosaur diversity through 170 Ma of the Mesozoic.
In many hypotheses of adaptive radiation, ecological speciation is an important process generating both morphological and taxonomic diversity (e.g., [2]; but see [46]), according to which ecological differentiation is essentially simultaneous with lineage splitting [12]. In consequence, many large-scale studies of adaptive radiation have focussed on diversification rates (e.g., [17],[21],[47]). A correlation between diversification rates and morphological rates is consistent with adaptive radiation (e.g., [15]). However, even when this can be demonstrated, the occurrence of ecological speciation is difficult (perhaps impossible) to test in clades even only a few Ma old [48]. Methods for estimating diversification rates on non-ultrametric trees (e.g., those including deep time data) have recently become available [49]. However, these methods require accurate estimates of sampling probability during discrete time intervals, and it is not clear that it is possible to obtain such estimates from the dinosaur fossil record, which contains many taxa known only from single occurrences. Therefore, our study focuses on the predictions of niche-filling models of morphological evolution during adaptive radiation, as done in some previous studies (e.g., [6],[13]).
Results
Most of the earliest dinosaurs weighed 10–35 kg (Figure 1); Herrerasaurus was exceptionally large at 260 kg. Maximum body masses increased rapidly to 1,000–10,000 kg in sauropodomorphs, with especially high masses in early sauropods such as Antetonitrus (5,600 kg; Norian, Late Triassic) and Vulcanodon (9,800 kg; Early Jurassic), whereas minimum body masses of 1–4 kg were attained by Late Triassic ornithischians and theropods (Figure 1). Jurassic Heterodontosauridae (∼0.7 kg [50]), Middle Jurassic and younger Paraves (e.g., Epidexipteryx, 0.4 kg; Anchiornis, 0.7 kg), and Cretaceous Avialae (birds: 13–16 g to 190 kg [51]) extended this lower body size limit (Table 1). Archaeopteryx weighed 0.99 kg (the largest, subadult specimen [52]) and the Cretaceous sauropod Argentinosaurus weighed approximately 90,000 kg (Table 1). Our full set of mass estimates is available in Dataset S1 and a summary is presented in Table 1.
Table 1. Estimated masses in kilograms of smaller- and larger-bodied adult representatives of major dinosaur groups, given to two significant figures. The standard error of all mass estimates is 0.135 log10(kg) [40].
| Clade | Smaller masses | Larger masses | ||
| Theropoda | ||||
| Theropoda (non-maniraptoran) | Sinosauropteryx prima | 0.99 | Tyrannosaurus rex | 7,700 |
| Procompsognathus triassicus | 1.13 | Giganotosaurus carolinii | 6,100 | |
| Maniraptora (non-avialan) | Parvicursor remotus | 0.14 | Suzhousaurus megatherioides | 3,100 |
| Rahonavis ostromi | 0.58 | Gigantoraptor erlianensis | 2,000 | |
| Avialae | Qiliania graffini | 0.013 | Gargantuavis philoinos | 190 |
| Iberomesornis romerali | 0.016 | Hesperornis crassipes | 24 | |
| Sauropodomorpha | ||||
| Basal Sauropodomorpha | Pampadromaeus barberenai | 8.5 | Lufengosaurus magnus | 2,300 |
| Sauropoda | Magyarosaurus dacus | 750 | Argentinosaurus huinculensis a | 90,000 |
| Europasaurus holgeri | 1,000 | Brachiosaurus altithorax | 56,000 | |
| Lirainosaurus astibiae | 1,800 | Turiasaurus riodevensis | 51,000 | |
| Ornithischia | ||||
| Heterodontosauridae | Fruitadens haagarorum | 0.73 | ||
| Tianyulong confuciusi | 0.74 | |||
| Stegosauria | Kentrosaurus aethiopicus | 1,600 | Dacentrurus armatus | 7,400 |
| Ankylosauria | Saichania chulsanensis | 610 | Ankylosaurus magniventris | 4,800 |
| Pachycephalosauria | Stegoceras validum | 16 | Pachycephalosaurus wyomingensis | 370 |
| Basal Ceratopsia | Psittacosaurus sinensis | 4.1 | Leptoceratops gracilis | 420 |
| Ceratopsidae | Centrosaurus apertus | 2500 | Triceratops horridus | 14,000 |
| Basal Iguanodontia | Mochlodon vorosi | 31 | Iguanodon bernissartensis | 15,000 |
| Hadrosauroidea | Gilmoreosaurus mongoliensis | 1,300 | Edmontosaurus regalis | 7,600 |
| “Probactrosaurus” mazongshanensis | 1,500 | Shantungosaurus giganteus | 17,000 | |
Only a referred femur of Argentinosaurus is known: estimating its humeral circumference from the least-squares regression relationship between humeral and femoral circumferences for large sauropods (femoral circumferences >400 mm) yields a mass estimate of 67,400–124,000 kg (95% prediction interval).
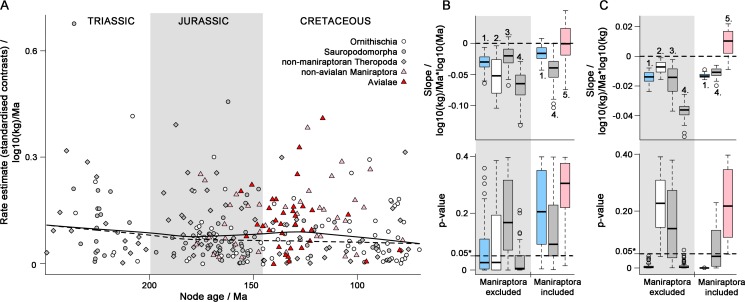
Our node height tests indicate that evolutionary rate estimates at phylogenetic nodes (standardised phylogenetically independent contrasts [39]) vary inversely with log-transformed stratigraphic age for most phylogenies (Figure 2). This relationship is significant (based on robust regression [14],[53]) for most phylogenies of non-maniraptoran dinosaurs, and for ornithischians and non-maniraptoran theropods when analysed separately (Figure 2B). This result is weakened, and becomes non-significant, when Triassic nodes are excluded (Figure S1).
Figure 2. Node height test for early burst of rates of dinosaur body mass evolution.
(A) Nodal evolutionary rate estimates (standardised independent contrasts [39],[89]) versus node age for data excluding (dashed lowess line) and including (solid lowess line) Maniraptora. (B–C) Box-and-whisker plots detailing results of: (B) robust regression of evolutionary rate on node age: slope (upper plot) and p-value (lower plot); (C) robust regression of evolutionary rate on nodal body mass: slope (upper plot) and p-value (lower plot). In (B–C) dashed lines occur at zero (upper plots) and 0.05 (lower plots: threshold for statistical significance). 1 = Dinosauria; 2 = Ornithischia; 3 = Sauropodomorpha; 4 = Theropoda; and 5 = Maniraptora.
Declining evolutionary rates through time are not found in any analyses including maniraptorans. Indeed, when maniraptorans are added to analyses of Dinosauria, a burst of high nodal rate estimates is evident in lowess lines spanning the Middle Jurassic–Early Cretaceous interval of maniraptoran diversification (Figure 2A). Maniraptorans have a weakly positive (non-significant) relationship between evolutionary rates and body mass, and do not show diminishing evolutionary rates through time (Figure 2B–C). This contrasts with non-maniraptoran dinosaurs, in which evolutionary rates vary inversely with body mass (Figure 2C).
Maximum-likelihood models [6],[38] were fitted to phylogenies calibrated to stratigraphy using the “equal” and “mbl” (minimum branch length) methods (see Materials and Methods ), and complement the results of our node height tests in showing support for early burst models only in analyses excluding Maniraptora (Table 2; Figure S2). Note, however, that the maximum-likelihood method has less statistical power to detect early burst patterns than does the node height test when even a small number of lineages escape from the overall pattern of declining rates through time [14]. Two models that predict saturation of trait variance through a clade's history were commonly supported in our analyses: the early burst model of exponentially declining evolutionary rates through time, and the Ornstein–Uhlenbeck (OU) model of attraction to a “trait optimum” value. Other models (e.g., Brownian motion, stasis) had negligible AICc weights in all or most (directional trend model) analyses (AICc is Akaike's information criterion for finite sample sizes).
Table 2. Summary of maximum-likelihood model-fitting approaches, AICc weights (see also Figure S2), and parameter values provided in the form “median (minimum–maximum)” over a set of 60 time-calibrated phylogenies (for AICc weights) or for those phylogenies in which the model received an AICc weight greater than 0.3 (the number of which is given in the column “Number”).
| Early burst | AICc weight | Number (weight>0.3) | β0 | a | ||
| Dinosauria | 0.0000 (0–0.004) | 0 | NA | NA | ||
| Dinosauria (non-maniraptoran) | 0.9615 (0–1) | 33 | 0.043 (0.031–0.064) | −0.014 (−0.008–0.016) | ||
| Ornithischia | 0.6445 (0.158–0.999) | 50 | 0.039 (0.020–0.057) | −0.010 (−0.005–0.017) | ||
| Sauropodomorpha | 0.6945 (0.002–1) | 46 | 0.033 (0.016–0.081) | −0.017 (−0.005–0.017) | ||
| Theropoda | 0.0000 (0–0) | 0 | NA | NA | ||
| Theropoda (non-maniraptoran) | 0.7745 (0.048–0.999) | 47 | 0.049 (0.033–0.085) | −0.014 (−0.011–0.021) | ||
| Maniraptora | 0.0000 (0–0.0450) | 0 | NA | NA |
Parameters: β, Brownian variance (log10kg2/Ma) (∼evolutionary rate; stochastic rate for Ornstein–Uhlenbeck [OU] models; initial rate [β0] in early burst models); a, a parameter describing variation in evolutionary rates through time in early burst models; μ, the mean step length (log10kg/Ma), indicating directional evolution in trend models; α, the strength of attraction to a macroevolutionary optimum (θ) in OU models; Z0, the ancestral node value (log10kg) in OU models; θ, the macroevolutionary optimum (log10kg) in OU models.
Early burst models received high AICc weights for analyses of ornithischians, non-maniraptoran theropods, and non-maniraptoran dinosaurs when using the “equal” branch length calibration method (Table 2; Figure S2). Early burst models had comparable AICc weights to Ornstein–Uhlenbeck models for sauropodomorphs when using the “equal” branch length calibration method, and for ornithischians and non-maniraptoran theropods when using the “mbl” method. Early burst models had generally lower AICc weights for non-maniraptoran dinosaurs and for sauropodomorphs when using the “mbl” branch length calibration method (Table 2; Figure S2). Support from some phylogenies for Ornstein–Uhlenbeck models of attraction to a large body size optimum from small ancestral body sizes [54],[55] in ornithischians [56], non-maniraptoran theropods, and especially sauropodomorphs and non-maniraptoran dinosaurs (Table 2; Figure S2), suggests the occurrence of Cope's rule in dinosaurs. All phylogenies provide strong support for this pattern in maniraptorans (Table 2).
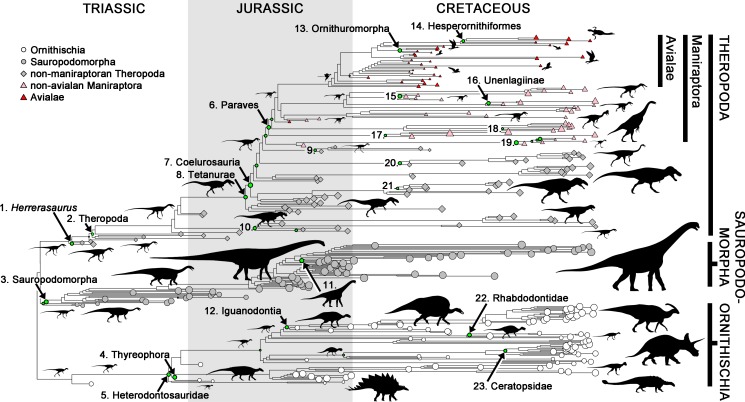
Exceptionally high rates at individual nodes in our phylogenies were identified as down-weighted datapoints in robust regression analyses [14],[53]. Five sets of exceptional nodes in the Triassic–Early Jurassic represent rapid evolutionary shifts from primitive masses around 10–35 kg to large body masses in derived sauropodomorphs (>1,000 kg), armoured ornithischians (Thyreophora; Figure 1B) and theropods (Herrerasaurus, and derived taxa such as Liliensternus (84 kg) and Dilophosaurus (350 kg)), and to smaller body sizes in heterodontosaurid ornithischians (Figure 3; Table 3). Rapid body size changes were rare in later ornithischians and sauropodomorphs, which each show only one exceptional Jurassic node, marking the origin of body sizes greater than 1,000 kg in derived iguanodontians, and of island dwarfism in the sauropod Europasaurus [57]. By contrast, up to six exceptional Jurassic nodes occur in theropod evolution, with especially high contrasts at the origins of body sizes exceeding 750 kg in Tetanurae, and marking phylogenetically nested size reductions on the line leading to birds: in Coelurosauria (e.g., Ornitholestes, 14 kg; Zuolong, 88 kg) and in Paraves, which originated at very small body masses around 1 kg [58].
Figure 3. Dinosaur phylogeny showing nodes with exceptional rates of body size evolution.
Exceptional nodes are numbered and indicated by green filled circles with diameter proportional to their down-weighting in robust regression analyses (Appendix S1). Details of these nodes are given in Table 2. The sizes of shapes at tree tips are proportional to log10(mass), and silhouettes are indicative of approximate relative size within some clades. The result from one tree calibrated to stratigraphy by imposing a minimum branch duration of 1 Ma is shown; other trees and calibration methods retrieve similar results. Silhouettes used were either previously available under Public Domain or with permission from the artists. Non-avialan dinosaur silhouettes used with thanks to the artist, Scott Hartman. Avialan silhouettes are modified from work by Nobumichi Tamura, and /Archaeopteryx/ from Mike Keesey.
Table 3. Details of body size changes at exceptional nodes indicated in Figure 3.
| Node | Description | Clade | Date | Polarity | Hypothesis |
| 1 | Origin of large body size in the early theropod Herrerasaurus (260 kg) | Thero. | Triassic | Increase | Macropredation |
| 2 | Origin of large body size in derived theropods such as Liliensternus (84 kg) and Dilophosaurus (350 kg) | Thero. | Triassic | Increase | Macropredation |
| 3 | Origin of large body size exceeding 1,000 kg in sauropodomorphs such as Plateosauravus (1,300 kg) and sauropods (Table 1) | Sauro. | Triassic | Increase | Bulk herbivory |
| 4 | Origin of large body size in armoured ornithischian dinosaurs (thyreophorans; Figure 1B) | Ornith. | Triassic/Jurassic | Increase | Bulk herbivory |
| 5 | Origin of small body size in heterodontosaurid ornithischians (∼0.7 kg; Table 1) | Ornith. | Triassic/Jurassic | Decrease | Specialised herbivory |
| 6 | Origin of small body size in Paraves, which has very small primitive body mass—around 1 kg (Anchiornis, 0.68 kg; Microraptor, 1.5 kg; Archaeopteryx, 0.97 kg (subadult)) | Thero. | Jurassic | Decrease | ? |
| 7 | Origin of small body size in Coelurosauria (e.g., Ornitholestes, 14 kg; Zuolong, 88 kg) | Thero. | Jurassic | Decrease | ? |
| 8 | Origin of large body size in Tetanurae (from 750 kg in Piatnitzkysaurus). | Thero. | Jurassic | Increase | Increased macropredation |
| 9 | Origin of small body size in compsognathid coelurosaurs (Compsognathus, 1.6–2.3 kg) | Thero. | Jurassic | Decrease | ? |
| 10 | Origin of large body size in some ceratosaurs (Ceratosaurus, 970 kg) | Thero. | Jurassic | Increase | Increased macropredation |
| 11 | Origin of small body size in the island dwarf sauropod Europasaurus (1,000 kg) | Sauro. | Jurassic | Decrease | Island dwarfing |
| 12 | Origin of large body sizes exceeding 1,000 kg in derived iguanodontians such as Camptosaurus | Ornith. | Jurassic | Increase | Bulk herbivory |
| 13 | Origin of large body size in the ornithuromorph birds Yanornis (1.5 kg) and Yixianornis (0.31 kg), compared with related taxa such as Longicrusavis (0.052 kg) and Hongshanornis (0.031 kg) | Thero. | Cretaceous | Increase | ?Wading |
| 14 | Origin of large body size in aquatic hesperornithiform birds (e.g., Baptornis, 4.9 kg; Hesperornis, 24 kg) | Thero. | Cretaceous | Increase | Aquatic life |
| 15 | Origin of large body size in Tianyuraptor (20 kg) compared with other microraptoran paravians (e.g., Graciliraptor, 1.8 kg; Microraptor, 1.5 kg) | Thero. | Cretaceous | Increase | ? |
| 16 | Origin of large body size in the unenlagiine dromaeosaurids Unenlagia (63 kg) and Austroraptor (519 kg) | Thero. | Cretaceous | Increase | Macropredation |
| 17 | Origin of large body size in herbivorous therizinosaurian maniraptorans (e.g., Falcarius, 84 kg; Suzhousaurus, 3,000 kg) | Thero. | Cretaceous | Increase | Bulk herbivory |
| 18 | Origin of large body size in the oviraptorosaur Gigantoraptor (2,000 kg) | Thero. | Cretaceous | Increase | ? |
| 19 | Origin of small body size in parvicursorine alvarezsauroids.(e.g., Parvicursor, 0.14 kg; Mononykus, 4.7 kg) | Thero. | Cretaceous | Decrease | ? |
| 20 | Origin of large body size in ornithomimosaurian coelurosaurs (e.g., Shenzhousaurus, 17 kg; Gallimimus, 480 kg; Beishanlong, 620 kg) | Thero. | Cretaceous | Increase | ?Herbivory |
| 21 | Origin of large body sizes in carcharodontosaurid tetanurans (Giganotosaurus, 6,100 kg; Mapusaurus, 4,100 kg; Carcharodontosaurus, 3,000 kg) | Thero. | Cretaceous | Increase | Increased macropredation |
| 22 | Origin of small body size in island dwarf rhabdodontid iguanodontians (e.g., Mochlodon vorosi, 31 kg) | Sauro. | Cretaceous | Decrease | Island dwarfing |
| 23 | Origin of large body size in Ceratopsidae (Figure 1B) | Ornith. | Cretaceous | Increase | Bulk herbivory |
Ornith., Ornithischia; Sauro., Sauropodomorpha; Thero., Theropoda.
The contrast between theropods and other dinosaurs is even greater in the Cretaceous, when no exceptional nodes occur in Sauropodomorpha, and only two in Ornithischia: at the origins of large-bodied Ceratopsidae and island dwarf rhabdodontid iguanodontians (e.g., Mochlodon [59]). At least nine shifts occurred during the same interval of theropod evolution, including seven in maniraptorans (Figure 3; Table 3).
Discussion
Niche-filling Patterns of Dinosaur Body Size Evolution
Patterns of dinosaur body size evolution are consistent with the niche-filling model of adaptive radiation [1],[4],[6]. Early dinosaurs exhibit rapid background rates of body size evolution, and a predominance of temporally rapid, order-of-magnitude shifts between body size classes in the Triassic and Early Jurassic. These shifts reflect radiation into disparate ecological niches such as bulk herbivory in large-bodied sauropodomorphs (e.g., [60]) and thyreophoran ornithischians, herbivory using a complex masticating dentition in small-bodied heterodontosaurids (e.g., [61],[62]), and increasing diversity of macropredation in large theropods (Table 3). Subsequently, rates of body size evolution decreased, suggesting saturation of coarsely defined body size niches available to dinosaurs in terrestrial ecosystems, and increasingly limited exploration of novel body size space within clades.
The early burst pattern of dinosaurian body size evolution is substantially weakened when Triassic data are excluded (Figure S1). This suggests that key innovations of Triassic dinosaurs (e.g., [63],[64]), and not the Triassic/Jurassic extinction of their competitors [37], drove the early radiation of dinosaur body sizes [34]. Indeed, phylogenetic patterns indicate that many basic ecomorphological divergences occurred well before the Triassic/Jurassic boundary.
It is not clear which innovations allowed dinosaurs to radiate [34], or whether the pattern shown here was part of a larger archosaurian radiation [65]. However, the evolution of rapid growth rates may have been important [64], especially in Sauropodomorpha [66], and the erect stance of dinosaurs and some other archosaurs [34] might have been a prerequisite for body size diversification via increased efficiency/capacity for terrestrial weight support [63].
Maniraptoran theropods are an exception to the overall pattern of declining evolutionary rates through time: exhibiting numerous instances of exceptional body size shifts, maintaining rapid evolutionary rates, and generating high ecological diversity [67],[68], including flying taxa. Although a previous study found little evidence for directional trends of body size increase in herbivorous maniraptoran clades [69], this does not conflict with our observation that some body size shifts in maniraptorans (and other coelurosaurs) coincide with the appearance of craniodental, or other, evidence for herbivory (Table 3; e.g., [67],[68],[70]).
Much of our knowledge of Late Jurassic and Early Cretaceous maniraptorans comes from a few well-sampled Chinese Lagerstätten, such as the Jehol biota. Without information from these exceptional deposits, we would have substantially less knowledge of divergence dates and ancestral body sizes among early maniraptorans. However, this is unlikely to bias comparisons between maniraptorans and other groups of dinosaurs for two reasons: (1) these deposits provide equally good information on the existence and affinities of small-bodied taxa in other clades, such as Ornithischia; and (2) exceptional information on early maniraptoran history should bias analyses towards finding an early burst pattern in maniraptorans. Inference of high early rates in Maniraptora would be more likely, due either to concentration of short branch durations at the base of the tree (especially using the “mbl” stratigraphic calibration method), or observation of additional body size diversity at the base of the tree that would remain undetected if sampling was poor. We cannot speculate as to the effects on our analyses of finding comparable Lagerstätten documenting early dinosaur history. However, there is currently little positive evidence that the general patterns of body size evolution documented here are artefactual.
Many stratigraphically younger dinosaurs, especially non-maniraptorans, exhibit large body size and had slow macroevolutionary rates, possibly due to scaling of generation times (e.g., [71],[72]). Scaling effects are observed across Dinosauria, but show substantial scatter (non-significant; Figure 2C) within Ornithischia and Sauropodomorpha, consistent with previous suggestions that scaling effects should be weak in dinosaurs because of the life history effects of oviparity [73]. Small dinosaurs (10–50 kg) had the highest evolutionary rates, and rates attenuated only weakly, or not at all, at sizes below 10 kg (Figure S3). This might have been key to maniraptoran diversification from small-bodied ancestors, and also explains the origins of fundamentally new body plans and ecotypes from small-bodied ancestors later in ornithischian history (Iguanodontia, Ceratopsidae; Figure 1).
Body Size, Ecological Diversity, and Cenozoic Survival
Maniraptora includes Avialae, the only dinosaur clade to frequently break the lower body size limit around 1–3 kg seen in other dinosaurs. It is likely that more niches are available to birds (and mammals) around 100 g in mass [41],[74], so obtaining smaller body sizes might have contributed to the ecological radiation of Mesozoic birds (e.g., [27],[75]). If the K/Pg extinction event was ecologically selective, vigorous ecological diversification may have given maniraptoran lineages a greater chance of survival: Avialae was the only dinosaurian clade to survive, perhaps because of the small body sizes of its members. Although the fossil record of birds is inadequate to test hypotheses of K/Pg extinction selectivity, it is clear that smaller-sized squamates and mammals selectively survived this event [76],[77]. Therefore, our results suggest that rapid evolutionary rates within Maniraptora paved the way for a second great adaptive radiation of dinosaurs in the wake of the K/Pg extinction event: the diversification of neornithine birds [21].
Implications for Adaptive Radiation Theory
Our findings complement recent studies of diversification rates in the avian crown group [3],[21], and suggest that birds, the most speciose class of tetrapods, arose from a long evolutionary history of continual ecological innovation. Our most striking finding is of sustained, rapid evolutionary rates on the line leading to birds (i.e., in maniraptorans) for more than 150 Ma, from the origin of dinosaurs until at least the end of the Mesozoic. Rates of evolution declined through time in most dinosaurs. However, this early burst pattern, which characterises the niche-filling model of adaptive radiation [6],[7], does not adequately describe evolution on the avian stem lineage. The recovered pattern of sustained evolutionary rates, and the repeated generation of novel ecotypes, suggests a key role for the maintenance of evolvability, the capacity for organisms to evolve, in the evolutionary success of this lineage. Evolvability might have also played a central role in the evolution of other major groups such as crustaceans [78] and actinopterygians [15], supporting its hypothesised importance in organismal evolution [79].
Rapid evolutionary rates observed during the early evolutionary history of Dinosauria, which decelerated through time in most subclades, indicate that much of the observed body size diversity of dinosaurs was generated by an early burst pattern of trait evolution. However, this pattern becomes difficult to detect when data from early dinosaurian history are not included in analyses (Figure S1), consistent with the observation that deep time data improve model inference in simulations [24]. The pruning of lineages by extinction might also overwrite the signals of ancient adaptive radiation in large neontological datasets. For example, Rabosky et al. [15] recovered slow evolutionary rates at the base of the actinopterygian tree, but the fossil record reveals substantial morphological and taxonomic diversity of extinct basal actinopterygian lineages [80],[81]. Although it has not yet been tested quantitatively, this diversity might have resulted from early rapid rates across Actinopterygii, as observed here across Dinosauria.
If our results can be generalised, they suggest that the unbalanced distribution of morphological and ecological diversity among clades results from the maintenance of rapid evolutionary rates over vast timescales in key lineages. These highly evolvable lineages may be more likely to lead to successful modern groups such as birds, whereas other lineages show declining evolutionary rates through time. Declining evolutionary rates in dinosaurian lineages off the line leading to birds indicate large-scale niche saturation. This might signal failure to keep pace with a deteriorating (biotic) environment (the Red Queen hypothesis [82],[83]), with fewer broad-scale ecological opportunities than those favouring the early radiation of dinosaurs. There is strong evidence for Red Queen effects on diversification patterns in Cenozoic terrestrial mammals [22], and it is possible that a long-term failure to exploit new opportunities characterises the major extinct radiations of deep time (and depauperate modern clades), whether or not it directly caused their extinctions.
Materials and Methods
We used phylogenetic comparative methods to analyse rates of dinosaur body mass evolution [6],[14],[38],[39] (Appendix S1). Body mass, accompanied by qualitative observations (Table 3), was used as a general ecological descriptor. Body mass was estimated for all dinosaurs for which appropriate data were available (441 taxa; Dataset S1) using the empirical scaling relationship of limb robustness (stylopodial circumference) with body mass, derived from extant tetrapods [40] (Appendix S1). We analysed log10-transformed data (excluding juveniles), which represent proportional changes in body mass.
Stylopodial shaft circumferences are infrequently reported in the literature, so many were taken from our own measurements, or were calculated from shaft diameters (Appendix S1). Previous large datasets of dinosaurian masses were based on substantially less accurate methods, using the relationship between linear measurements (e.g., limb bone lengths) and volumetric models of extinct dinosaurs ([84]–[86]; reviewed by [40]).
Quantitative macroevolutionary models were tested on composite trees compiled from recent, taxon-rich cladograms of major dinosaur groups (Appendix S1; Figure S4, Figure S5, Figure S6, Figure S7). Phylogenetic uncertainty was reflected by analysing alternative topologies and randomly resolved polytomies (Appendix S1). Tip heights and branch durations were stratigraphically calibrated, and zero-length branches were “smoothed” using two methods: (1) by sharing duration equally with preceding non-zero length branches (the “equal” method [87]); and (2) by imposing a minimum branch length of 1 Ma (the “mbl” method [88]).
We used maximum-likelihood model comparison [6],[38] and “node height” test [14],[39] methods (Appendix S1) to test the prediction of the niche-filling hypothesis: that rates of morphological evolution diminish exponentially through time after an adaptive radiation [1],[2],[4]. The node height test treats standardised independent contrasts [89] as nodal estimates of evolutionary rate [39] and tests for systematic deviations from a uniform rate Brownian model, using regression against log-transformed geological age (robust regression [14],[53]). We also regressed standardised contrasts against nodal body mass estimates (a proxy for generation time and other biological processes that might influence evolutionary rates). As well as testing for a “background” model of declining evolutionary rates through time, robust regression identifies and down-weights single nodes deviating substantially from the overall pattern [14],[53]. These nodes represent substantial, temporally rapid, niche-shift events [14], following the macroecological principle that organisms in different body size classes inhabit different niches and have different energetic requirements [41]. We used lowess lines to visualise non-linear rate variation with time and body mass.
Exponentially declining rates of evolution through time, predicted by the niche-filling model of adaptive radiation [1]–[3], were also tested by comparing the fit of an early burst model [6],[7] with other commonly used models: Brownian motion, directional evolution (“trend”), the Ornstein–Uhlenbeck model of evolution attracted to an optimum value, and stasis (“white noise”) [38],[56],[90] (Appendix S1). Explicit mathematical models of trait evolution on our phylogenies were fitted using the R packages GEIGER version 1.99–3 [91] and OUwie version 1.33 [55] (for Ornstein–Uhlenbeck (OU) models only), and compared using AICc [92],[93]. Unlike GEIGER, OUwie allows estimation of a trait optimum (θ) that is distinct from the root value (Z0) in OU models. Values from GEIGER and OUwie are directly comparable: identical log likelihood, AICc, and parameter estimates are obtained for test datasets when fitting models implemented in both packages (Brownian motion in all instances; and OU models when θ = Z0 for ultrametric trees); although note that comparable standard error values entered to the OUwie function of OUwie 1.33 are the square of those entered to the fitContinuous function of Geiger 1.99–3. The algorithm used to fit OU models in GEIGER 1.99–3 is inappropriate for non-ultrametric trees (personal communication, Graham Slater to R. Benson, December 2013). This problem is specific to OU models implemented by GEIGER 1.99–3, and does not affect the other models that we tested. GEIGER 1.99–3 fits models of trait evolution using independent contrasts, after rescaling the branch lengths of the phylogenetic tree according to the model considered [7]. For all models, except the OU model in the case of non-ultrametric trees, the covariance between two taxa i and j can be written as a function of the path length sij shared between the two taxa (e.g., [6],[7]). The tree can thus easily be rescaled by applying this function to the height of each node before computing independent contrasts. In the case of the OU model, the covariance between two taxa i and j is a function of both the shared (pre-divergence) portion of their phylogenetic history and the non-shared (post-divergence) portion [54]. In the case of an ultrametric tree, the non-shared portion can also be written as a function of sij (it is simply the total height T of the tree, minus sij [90],[94]), and the corresponding scaling function can be applied to the tree (this is what is performed in GEIGER 1.99.3). However, in the case of a non-ultrametric tree, the post-divergence portion of the covariance cannot be written as a function of sij, so there is no straightforward scaling function to apply. Instead, it is necessary to fit the model by maximum likelihood after computing the variance–covariance matrix. This is what is implemented in OUwie, and now in GEIGER 2.0 (personal communication, Josef Uyeda to R. Benson, January 2014).
Our data and analytical scripts are available at DRYAD [95].
Supporting Information
Node height test for early burst of rates of dinosaur body mass evolution excluding Triassic nodes. Results of robust regression of evolutionary rate on node age: (A) slope; (B) p-value. Dashed lines occur at zero (A) and 0.05 (B); 1 = Dinosauria; 2 = Ornithischia; 3 = Sauropodomorpha; 4 = Theropoda; and 5 = Maniraptora.
(TIF)
AICc weights of maximum likelihood models using different trees and time calibration methods. AICc weights are shown for early burst (1–5), trend (6), and Ornstein–Uhlenbeck (7) models. (A) Trees including the Yates topology for non-sauropodan sauropodomorphs (Figure S6), and calibrated using the “equal” method ( Materials and Methods ). (B) Trees including the Upchurch topology for non-sauropodan sauropodomorphs (Figure S7), and calibrated using the “equal” method. (C) Trees including the Yates topology for non-sauropodan sauropodomorphs, and calibrated using the “mbl” method ( Materials and Methods ). (D) Trees including the Upchurch topology for non-sauropodan sauropodomorphs, and calibrated using the “mbl” method.
(TIF)
A possible non-linear relationship between macroevolutionary rate and nodal body mass. (A) Based on one phylogeny calibrated using the “equal” method ( Materials and Methods ). (B) Based on one phylogeny calibrated using the “mbl” method ( Materials and Methods ). The (solid) lowess lines suggests that rates decrease with body mass above ∼10−50 kg, but might also decline with a shallower gradient below ∼10−50 kg. The dashed lines show the fitted linear robust regressions.
(TIF)
Composite tree of ornithischian dinosaur relationships used in the present study. Polytomies were resolved randomly prior to analyses. Details of tree construction are given in Appendix S1.
(TIF)
Composite tree of theropod dinosaur relationships used in the present study. Polytomies were resolved randomly prior to analyses. Details of tree construction are given in Appendix S1.
(TIF)
Composite tree of sauropodomorph relationships used in the present study, using the Yates topology for non-sauropodans. Polytomies were resolved randomly prior to analyses. Details of tree construction are given in Appendix S1.
(TIF)
Composite tree of sauropodomorph relationships used in the present study, using the Upchurch et al. topology for non-sauropodans. Polytomies were resolved randomly prior to analyses. Details of tree construction are given in Appendix S1.
(TIF)
Summary of ordinary least-squares regression relationships between femoral and humeral anteroposterior and mediolateral shaft diameters for groups. N, sample size; R2, coefficient of determination.
(DOC)
Proportions of phylogenies for which data simulated under a constant rate Brownian motion model generated robust regression slopes (node height test) shallower than those observed in the data in fewer than 0.05, 0.10, 0.15, or 0.20 of simulated datasets. Analyses excluding Maniraptora are shaded in grey, and results based only on phylogenies calibrated to stratigraphy different methods (see Materials and Methods ) are additionally presented for Dinosauria. ** indicates cases in which all phylogenies reject the constant rate model at the specified threshold, and * indicates cases in which most phylogenies reject the constant rate model at the specified threshold. Values should not be regarded as p-values, but generally concur with the p-values of our robust regression fits (Figure 2B).
(DOC)
Additional methods and results.
(DOC)
Complete dataset and mass estimates.
(XLS)
Acknowledgments
We thank Graham Slater, Josef Uyeda, Rich FitzJohn, and Jeremy Beaulieu for discussion. We thank Ronan Allain, John Bird, Stephen Brusatte, Sérgio Cabreira, Jonah Choiniere, Serjoscha Evers, Maria Malabarba, Octavio Mateus, Jay Nair, Attila Õsi, Dennis Parsons, Diego Pol, Stephen Poropat, Toru Sekiya, Virginia Tidwell, Peggy Vincent, John Whitlock, and Thomas Williamson for sharing measurements.
Abbreviations
- AICc
Akaike's information criterion for finite sample sizes
- Ma
million years
- mbl
minimum branch length
Funding Statement
Parts of this project were supported by a Leverhulme Research Grant (to Paul Upchurch) RPG-129. PDM is funded by an Imperial College Junior Research Fellowship. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Simpson GG (1953) The Major Features of Evolution. New York: Columbia University Press. 434 p. [Google Scholar]
- 2.Schluter D (2000) The Ecology of Adaptive Radiation. Oxford: Oxford University Press. 288 p. [Google Scholar]
- 3. Alfaro ME, Santini F, Brock C, Alamillo H, Dornburg H, et al. (2009) Nine exceptional radiations plus high turnover explain species diversity in jawed vertebrates. Proc Natl Acad Sci USA 106: 13410–13414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Etienne RS, Haegemann B (2012) A conceptual and statistical framework for adaptive radiations with a key role for diversity dependence. Am Nat 180: E75–E89. [DOI] [PubMed] [Google Scholar]
- 5. Glor RE (2010) Phylogenetic insights on adaptive radiation. Annu Rev Ecol Syst 41: 251–270. [Google Scholar]
- 6. Harmon LJ, Losos JB, Davies TJ, Gillespie RG, Gittleman JL, et al. (2010) Early bursts of body size and shape evolution are rare in comparative data. Evolution 64: 2385–2396. [DOI] [PubMed] [Google Scholar]
- 7. Blomberg SP, Garland T, Ives AR (2003) Testing for phylogenetic signal in comparative data: behavioural traits are more labile. Evolution 57: 717–745. [DOI] [PubMed] [Google Scholar]
- 8.Losos JB. 2009. Lizards in an Evolutionary Tree. Berkeley: University of California Press. 507 p. [Google Scholar]
- 9. Kornfield I, Smith PF (2000) African cichlid fishes: model systems for evolutionary biology. Annu Rev Ecol Syst 31: 163–196. [Google Scholar]
- 10.Grant PR, Grant BR (2008) How and Why Species Multiply: the Radiation of Darwin's Finches. Princeton: Princeton University Press. 218 p. [Google Scholar]
- 11. Streelman JT, Danley PD (2003) The stages of vertebrate evolutionary radiation. Trends Ecol Evol 18: 126–131. [Google Scholar]
- 12. Rundle HD, Nosil P (2005) Ecological speciation. Ecol Lett 8: 336–352. [Google Scholar]
- 13. Slater GJ, Price SA, Santini F, Alfaro ME (2010) Diversity versus disparity and the radiation of modern cetaceans. Proc R Soc B 277: 3097–3104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Slater GJ, Pennell MW (2013) Robust regression and posterior predictive simulation increase power to detect early bursts of trait evolution. Syst Biol 10.1093/sysbio/syt066 [DOI] [PubMed] [Google Scholar]
- 15. Rabosky DL, Santini F, Eastman J, Smith SA, Sidlauskas B, et al. (2013) Rates of speciation and morphological evolution are correlated across the largest vertebrate radiation. Nat Commun 4: 1958. [DOI] [PubMed] [Google Scholar]
- 16. Lee MS, Soubrier J, Edgecombe GD (2013) Rates of phenotypic and genomic evolution during the Cambrian explosion. Curr Biol 23: 1889–1895. [DOI] [PubMed] [Google Scholar]
- 17. Bininda-Emonds ORP, Cardillo M, Jones KE, MacPhee RDE, Beck RMD, et al. (2007) The delayed rise of present-day mammals. Nature 446: 507–512. [DOI] [PubMed] [Google Scholar]
- 18. Cooper N, Purvis A (2010) Body size evolution in mammals: complexity in tempo and mode. Am Nat 175: 727–738. [DOI] [PubMed] [Google Scholar]
- 19. Slater GJ (2013) Phylogenetic evidence for a shift in the mode of mammalian body size evolution at the Cretaceous-Palaeogene boundary. Methods Ecol Evol 4: 734–744. [Google Scholar]
- 20. Harmon LJ, Schulte JA 2nd, Larson A, Losos JB (2003) Tempo and mode of evolutionary radiation in iguanian lizards. Science 301: 961–964. [DOI] [PubMed] [Google Scholar]
- 21. Jetz W, Thomas GH, Joy JB, Hartmann K, Mooers AO (2012) The global diversity of birds in space and time. Nature 491: 444–448. [DOI] [PubMed] [Google Scholar]
- 22. Quental TB, Marshall CR (2013) How the Red Queen drives terrestrial mammals to extinction. Science 341: 290–292. [DOI] [PubMed] [Google Scholar]
- 23. Losos JB (2010) Adaptive radiation, ecological opportunity, and evolutionary determinism. Am Nat 175: 623–639. [DOI] [PubMed] [Google Scholar]
- 24. Slater GJ, Harmon LJ, Alfaro ME (2012) Integrating fossils with molecular phylogenies improves inference of trait evolution. Evolution 66: 3931–3944. [DOI] [PubMed] [Google Scholar]
- 25. Foote M (1994) Morphological disparity in Ordovician–Devonian crinoids and the early saturation of morphological space. Paleobiology 20: 320–344. [Google Scholar]
- 26. Wills MA, Briggs DEG, Fortey RA (1994) Disparity as an evolutionary index: a comparison of Cambrian and Recent arthropods. Paleobiology 20: 93–130. [Google Scholar]
- 27. Benson RBJ, Choiniere JN (2013) Rates of dinosaur limb evolution provide evidence for exceptional radiation in Mesozoic birds. Proc R Soc B 280: 20131780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Ruta M, Wagner PJ, Coates MI (2006) Evolutionary patterns in early tetrapods. 1. Rapid initial diversification followed by decrease in rates of character change. Proc R Soc B 273: 2107–2111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Westoll (1949) On the evolution of the Dipnoi. Jepsen GL, Simpson GG, Mayr E, editors. Genetics, Paleontology and Evolution. Princeton: Princeton University Press. pp. 121–184. [Google Scholar]
- 30. Lloyd GT, Wang SC, Brusatte SL (2012) Identifying heterogeneity in rates of morphological evolution: discrete character change in the evolution of lungfish (Sarcopterygii; Dipnoi). Evolution 66: 330–348. [DOI] [PubMed] [Google Scholar]
- 31. Wagner P (1997) Patterns of morphological diversification among the Rostroconchia. Paleobiology 23: 115–150. [Google Scholar]
- 32.Carrano MT (2006) Body-size evolution in the Dinosauria. Carrano MT, Gaudin TJ, Blob RW, Wible JR, editors. Amniote Paleobiology. Chicago: University of Chicago Press. pp. 225–268 [Google Scholar]
- 33. Brusatte SL, Benton MJ, Ruta M, Lloyd GT (2008) The first 50 Myr of dinosaur evolution: macroevolutionary pattern and morphological disparity. Biol Lett 4: 733–736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Irmis RB (2011) Evaluating hypotheses for the early diversification of dinosaurs. T Roy Soc Edin—Earth 101: 397–426. [Google Scholar]
- 35. Fastovsky DE, Sheehan (2005) The extinction of the dinosaurs in North America. GSA Today 15: 4–10. [Google Scholar]
- 36. Upchurch P, Mannion PD, Benson RBJ, Butler RJ, Carrano MT (2011) Geological and anthropogenic controls on the sampling of the terrestrial fossil record: a case study from the Dinosauria. Spec Publ Geol Soc Lond 358: 209–240. [Google Scholar]
- 37. Olsen PE, Kent DV, Sues H-D, Koeberl C, Huber H, et al. (2002) Ascent of dinosaurs linked to an iridium anomaly at the Triassic–Jurassic boundary. Science 296: 1305–1307. [DOI] [PubMed] [Google Scholar]
- 38. Pagel M (1999) Inferring the historical patterns of biological evolution. Nature 401: 877–884. [DOI] [PubMed] [Google Scholar]
- 39. Freckleton RP, Harvey PH (2006) Detecting non-Brownian trait evolution in adaptive radiations. PLoS Biol 4: e373 10.1371/journal.pbio.0040373 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Campione NE, Evans DC (2012) A universal scaling relationship between body mass and proximal limb bone dimensions in quadrupedal terrestrial tetrapods. BMC Biol 10: 1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Brown JH (1997) Macroecology. Chicago: University of Chicago Press. 269 p. [Google Scholar]
- 42. West GB, Woodruff WH, Brown JH (2002) Allometric scaling of metabolic rate from molecules and mitochondria to cells and mammals. Proc Natl Acad Sci USA 99: 2473–2478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Mitchell JS, Roopnarine PD, Angielczyk (2012) Late Cretaceous restructuring of terrestrial communities facilitated the end-Cretaceous mass extinction in North America. Proc Natl Acad Sci USA 109: 18857–18861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Clauss M, Steuer P, Müller DWH, Codron D, Hummel J (2013) Herbivory and body size: allometries of diet quality and gastrointestinal physiology, and implications for herbivore ecology and dinosaur gigantism. PLoS ONE 8: e68714 10.1371/journal.pone.0068714 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Mallon JC, Evans DC, Ryan MJ, Anderson JS (2013) Feeding height stratification among the herbivorous dinosaurs from the Dinosaur Park Formation (Upper Campanian) of Alberta, Canada. BM Ecol 13: 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Givinish TJ (1997) Adaptive radiation and molecular systematics: issues and approaches. Givinish TJ, Systma KJ, editors. Molecular Evolution and Adaptive Radiation. Cambridge: Cambridge University Press. pp. 1–54. [Google Scholar]
- 47. Guyer, Slowinski (1993) Testing whether certain traits have amplified diversification: an improved method based on a model of random speciation and extinction. Am Nat 142: 1019–1024. [DOI] [PubMed] [Google Scholar]
- 48. Rundell RJ, Price TD (2009) Adaptive radiation, nonadaptive radiation, ecological speciation and nonecological speciation. Trends Ecol Evol 24: 394–399. [DOI] [PubMed] [Google Scholar]
- 49. Stadler T, Kühnert D, Bonheoffer S, Drummond AJ (2013) Birth–death skyline plot reveals temporal changes of epidemic spread in HIV and hepatitis C virus (HCV). Proc Natl Acad Sci USA 110: 228–233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Butler RJ, Galton PM, Porro LB, Chiappe LM, Henderson DM, et al. (2009) Lower limits of ornithischian dinosaur body size inferred from a new Upper Jurassic heterodontosaurid from North America. Proc R Soc B 277: 375–381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Buffetaut E, Le Loeuff J, Mechin P, Mechin-Salessy A (1995) A large French Cretaceous bird. Nature 377: 110. [Google Scholar]
- 52. Erickson GM, Rauhut OWM, Zhou Z-H, Turner AH, Inouye BD, et al. (2009) Was dinosaurian physiology inherited by birds? Reconciling slow growth in Archaeopteryx . PLoS ONE 4: e7390 10.1371/journal.pone.0007390 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Huber PJ (1973) Robust regression: asymptotics, conjectures and Monte Carlo. Ann Stat 1: 799–821. [Google Scholar]
- 54. Hansen TF (1997) Stabilizing selection and the comparative analysis of adaptation. Evolution 51: 1341–1351. [DOI] [PubMed] [Google Scholar]
- 55. Beaulieau JM, Jhuwueng D-C, Boettiger C, O'Meara BC (2012) Modelling stablizing selection: expanding the Ornstein–Uhlenbeck model of adaptive evolution. Evolution 66: 2369–2383. [DOI] [PubMed] [Google Scholar]
- 56. Hunt G, Carrano MT (2010) Models and methods for analyzing phenotypic evolution in lineages and clades. Spec Pap Pal Soc 16: 245–269. [Google Scholar]
- 57. Sander PM, Mateus O, Laven T, Knötschke N (2006) Bone histology indicates insular dwarfism in a new Late Jurassic sauropod dinosaur. Nature 441: 739–741. [DOI] [PubMed] [Google Scholar]
- 58. Turner AH, Pol D, Clarke JA, Erickson GM, Norell MA (2007) A basal dromaeosaurid and size evolution preceding avian flight. Science 317: 1378–1381. [DOI] [PubMed] [Google Scholar]
- 59. Ősi A, Prondvai E, Butler R, Weishampel DB (2012) Phylogeny, histology and inferred body size evolution in a new rhabdodontid dinosaur from the Late Cretaceous of Hungary. PLoS ONE 7 (9) e44318 10.1371/journal.pone.0044318 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Sander PM, Christian A, Clauss M, Fechner R, Gee CT, et al. (2010) Biology of the sauropod dinosaurs: the evolution of gigantism. Biol Rev 86: 117–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Norman DB, Crompton AW, Butler RJ, Porro LB, Charig AJ (2011) The Lower Jurassic ornithischian dinosaur Heterodontosaurus tucki Crompton & Charig, 1962: cranial anatomy, functional morphology, taxonomy, and relationships. Zoo J Linn Soc 163: 182–276. [Google Scholar]
- 62. Sereno PC (2012) Taxonomy, morphology, masticatory function and phylogeny of heterodontosaurid dinosaurs. ZooKeys 226: 1–225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Charig AJ (1984) Competition between therapsids and archosaurs during the Triassic period: a review and synthesis of current theories. Ferguson MWJ, editor. The Structure, Development and Evolution of Reptiles. Symposia of the Zoological Society of London 52: 597–628. [Google Scholar]
- 64. Padian K, Ricqlés AJde, Horner JR (2001) Dinosaurian growth rates and bird origins. Nature 412: 405–408. [DOI] [PubMed] [Google Scholar]
- 65. Brusatte SL, Benton MJ, Lloyd GT, Ruta M, Wang SC (2011) Macroevolutionary patterns in the evolutionary radiation of archosaurs (Tetrapoda: Diapsida). T Roy Soc Edin–Earth 101: 367–382. [Google Scholar]
- 66. Sander PM, Klein N, Buffetaut E, Cuny G, Suteethorn V, et al. (2004) Adaptive radiation in sauropod dinosaurs: bone histology indicates rapid evolution of giant body size through acceleration. Naturwissenschaften 4: 165–173. [Google Scholar]
- 67.Barrett PM (2000) Prosauropods and iguanas: speculations on the diets of extinct reptiles. Sues H-D, editor. Evolution of Herbivory in Terrestrial Vertebrates. Cambridge: Cambridge University Press. pp. 42–78. [Google Scholar]
- 68. Zanno LE, Makovicky PJ (2010) Herbivorous ecomorphology and specialization patterns in theropod dinosaur evolution. Proc Natl Acad Sci USA 108: 232–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Zanno LE, Makovicky PJ (2013) No evidence for directional evolution of body mass in herbivorous theropod dinosaurs. Proc R Soc B 280: 20122526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Barrett PM (2005) The diet of ostrich dinosaurs (Theropoda: Ornithomimosauria). Palaeontology 48: 347–358. [Google Scholar]
- 71. Gingerich PD (2009) Rates of evolution. Ann Rev Ecol Syst 40: 657–675. [Google Scholar]
- 72. Evans AR, Jones D, Boyer AG, Brown JH, Costa DP, et al. (2012) The maximum rate of mammal evolution. Proc Natl Acad Sci USA 109: 4187–4190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Janis CM, Carrano MT (1992) Scaling of reproductive turnover in archosaurs and mammals: why are large terrestrial animals so rare? Acta Zool Fenn 28: 201–216. [Google Scholar]
- 74. Lomolino MV (1985) Body size of mammals on islands: the island rule re-examined. Am Nat 125: 310–316. [Google Scholar]
- 75.O'Connor J, Chiappe LM, Bell A (2011) Pre-modern birds: avian divergences in the Mesozoic. Dyke G, Kaiser G, editors. Living Dinosaurs: the Evolutionary History of Modern Birds. Oxford: Wiley-Blackwell. pp. 39–116. [Google Scholar]
- 76. Longrich NR, Bhullar B-AS, Gauthier JA (2012) Mass extinction of lizards and snake at the Cretaceous–Paleogene boundary. Proc Natl Acad Sci USA 52: 21396–21401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Wilson GP (2013) Mammals across the K/Pg boundary in northeastern Montana, USA: dental morphology and body-size patterns reveal extinction selectivity and immigrant-fueled ecospace filling. Paleobiol 39: 429–469. [Google Scholar]
- 78. Adamowicz SJ, Purvis A, Wills MA (2008) Increasing morphological complexity in multiple parallel lineages of the Crustacea. Proc Natl Acad Sci USA 105: 4786–4791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Vermeij GJ (1973) Biological versatility and Earth history. Proc Natl Acad Sci USA 70: 1936–1938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Janvier P (1996) Early Vertebrates. Oxford: Clarendon Press. 393 p. [Google Scholar]
- 81. Sallan LC, Friedman M (2012) Heads or tails: staged diversification in vertebrate evolutionary radiations. Proc R Soc B 279: 2025–2032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82. Van Valen L (1973) A new evolutionary law. Evol Theory 1: 1–30. [Google Scholar]
- 83. Benton MJ (2009) The Red Queen and the Court Jester: species diversity and the role of biotic and abiotic factors through time. Science 323: 728–732. [DOI] [PubMed] [Google Scholar]
- 84. Seebacher F (2001) A new method to calculate allometric length–mass relationships of dinosaurs. J Vert Paleontol 21: 51–60. [Google Scholar]
- 85. Mazzetta GV, Christiansen P, Fariña RA (2004) Giants and bizarres: body size of some southern South American Cretaceous dinosaurs. Hist Biol 2004: 1–13. [Google Scholar]
- 86. O'Gorman EJ, Hone DWE (2012) Body size distribution of the dinosaurs. PLoS ONE 7 (12) e51925 10.1371/journal.pone.0051925 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87. Brusatte SL, Benton MJ, Ruta M, Lloyd GT (2008) Superiority, competition, and opportunism in the evolutionary radiation of dinosaurs. Science 321: 1485–1487. [DOI] [PubMed] [Google Scholar]
- 88. Laurin M (2004) The evolution of body size, Cope's rule and the origin of amniotes. Syst Biol 53: 594–622. [DOI] [PubMed] [Google Scholar]
- 89. Felsenstein J (1985) Phylogenies and the comparative method. Am Nat 125: 1–15. [Google Scholar]
- 90. Butler MA, King AA (2004) Phylogenetic comparative analysis: a modelling approach for adaptive radiation. Am Nat 164: 683–695. [DOI] [PubMed] [Google Scholar]
- 91. Harmon LJ, Weir JT, Brock CD, Glor RE, Challenger W (2008) GEIGER: investigating evolutionary radiations. Bioinformatics 24: 129–131. [DOI] [PubMed] [Google Scholar]
- 92. Sugiura N (1978) Further analysis of the data by Akaike's information criterion and the finite corrections. Commun Statist—Theor Meth 7: 13–26. [Google Scholar]
- 93.Burnham KP, Anderson DR (2004) Model selection and multimodel inference. New York: Springer. 488 p. [Google Scholar]
- 94. Slater G (in press) Erratum: phylogenetic evidence for a shift in the mode of mammalian body size evolution at the Cretaceous–Paleogene boundary. Methods Ecol Evol [Google Scholar]
- 95. Benson RBJ, Campione NE, Carrano MT, Mannion PD, Sullivan C, et al. (2014) Rates of dinosaur body mass evolution indicate 170 million years of sustained ecological innovation on the avian stem lineage. Dryad Data Repository 10.5061/dryad.gr1qp. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Node height test for early burst of rates of dinosaur body mass evolution excluding Triassic nodes. Results of robust regression of evolutionary rate on node age: (A) slope; (B) p-value. Dashed lines occur at zero (A) and 0.05 (B); 1 = Dinosauria; 2 = Ornithischia; 3 = Sauropodomorpha; 4 = Theropoda; and 5 = Maniraptora.
(TIF)
AICc weights of maximum likelihood models using different trees and time calibration methods. AICc weights are shown for early burst (1–5), trend (6), and Ornstein–Uhlenbeck (7) models. (A) Trees including the Yates topology for non-sauropodan sauropodomorphs (Figure S6), and calibrated using the “equal” method ( Materials and Methods ). (B) Trees including the Upchurch topology for non-sauropodan sauropodomorphs (Figure S7), and calibrated using the “equal” method. (C) Trees including the Yates topology for non-sauropodan sauropodomorphs, and calibrated using the “mbl” method ( Materials and Methods ). (D) Trees including the Upchurch topology for non-sauropodan sauropodomorphs, and calibrated using the “mbl” method.
(TIF)
A possible non-linear relationship between macroevolutionary rate and nodal body mass. (A) Based on one phylogeny calibrated using the “equal” method ( Materials and Methods ). (B) Based on one phylogeny calibrated using the “mbl” method ( Materials and Methods ). The (solid) lowess lines suggests that rates decrease with body mass above ∼10−50 kg, but might also decline with a shallower gradient below ∼10−50 kg. The dashed lines show the fitted linear robust regressions.
(TIF)
Composite tree of ornithischian dinosaur relationships used in the present study. Polytomies were resolved randomly prior to analyses. Details of tree construction are given in Appendix S1.
(TIF)
Composite tree of theropod dinosaur relationships used in the present study. Polytomies were resolved randomly prior to analyses. Details of tree construction are given in Appendix S1.
(TIF)
Composite tree of sauropodomorph relationships used in the present study, using the Yates topology for non-sauropodans. Polytomies were resolved randomly prior to analyses. Details of tree construction are given in Appendix S1.
(TIF)
Composite tree of sauropodomorph relationships used in the present study, using the Upchurch et al. topology for non-sauropodans. Polytomies were resolved randomly prior to analyses. Details of tree construction are given in Appendix S1.
(TIF)
Summary of ordinary least-squares regression relationships between femoral and humeral anteroposterior and mediolateral shaft diameters for groups. N, sample size; R2, coefficient of determination.
(DOC)
Proportions of phylogenies for which data simulated under a constant rate Brownian motion model generated robust regression slopes (node height test) shallower than those observed in the data in fewer than 0.05, 0.10, 0.15, or 0.20 of simulated datasets. Analyses excluding Maniraptora are shaded in grey, and results based only on phylogenies calibrated to stratigraphy different methods (see Materials and Methods ) are additionally presented for Dinosauria. ** indicates cases in which all phylogenies reject the constant rate model at the specified threshold, and * indicates cases in which most phylogenies reject the constant rate model at the specified threshold. Values should not be regarded as p-values, but generally concur with the p-values of our robust regression fits (Figure 2B).
(DOC)
Additional methods and results.
(DOC)
Complete dataset and mass estimates.
(XLS)