Abstract
Several members of the Alkaline Phosphatase (AP) superfamily exhibit a high level of catalytic proficiency and promiscuity in structurally similar active sites. A thorough characterization of the nature of transition state for different substrates in these enzymes is crucial for understanding the molecular mechanisms that govern those remarkable catalytic properties. In this work, we study the hydrolysis of a phosphate diester, MpNPP−, in solution, two experimentally well-characterized variants of AP (R166S AP, R166S/E322Y AP) and wild type Nucleotide pyrophosphatase/phosphodiesterase (NPP) by QM/MM calculations in which the QM method is an approximate density functional theory previously parameterized for phosphate hydrolysis (SCC-DFTBPR). The general agreements found between these calculations and available experimental data for both solution and enzymes support the use of SCC-DFTBPR/MM for a semi-quantitative analysis of the catalytic mechanism and nature of transition state in AP and NPP. Although phosphate diesters are cognate substrates for NPP but promiscuous substrates for AP, the calculations suggest that their hydrolysis reactions catalyzed by AP and NPP feature similar synchronous transition states that are slightly tighter in nature compared to that in solution, due in part to the geometry of the bimetallic zinc motif. Therefore, this study provides the first direct computational support to the hypothesis that enzymes in the AP superfamily catalyze cognate and promiscuous substrates via similar transition states to those in solution. Our calculations do not support the finding of recent QM/MM studies by López-Canut and coworkers, who suggested that the same diester substrate goes through a much looser transition state in NPP/AP than in solution, a result likely biased by the large structural distortion of the bimetallic zinc site in their simulations. Finally, our calculations for different phosphate diester orientations and phosphorothioate diesters highlight that the interpretation of thio-substitution experiments is not always straightforward.
I. Introduction
Although a high-level of catalytic specificity has been regarded as an important hallmark of enzymes, it is increasingly recognized that many enzymes have promiscuous catalytic activities.1–5 Moreover, it has been proposed that catalytic promiscuity plays an important role in enzyme evolution since it can give an enzyme an evolution “head start”, providing a modest rate enhancement that is sufficient as a selective advantage1,6–9. Therefore, identifying factors that dictate the level of catalytic promiscuity in enzymes can help better understand enzyme evolution and improve design strategies for evolving new catalytic functions.
In this context, members in the Alkaline Phosphatase (AP) superfamily present striking examples of catalytic specificity and promiscuity.10,11 They have been demonstrated to catalyze the hydrolysis of a broad range of substrates that differ in charge, size, intrinsic reactivity and transition state (TS) nature12. For example, E. coli AP catalyzes the hydrolytic reaction of phosphate monoesters for its physiological function but also exhibits promiscuous activity for the hydrolysis of phosphate diesters and sulfate esters of diverse structural/chemical features. Similarly, although the main function of Nucleotide pyrophosphatase/phosphodiesterase (NPP) is to hydrolyze phosphate diesters, it can also cleave phosphate monoesters and sulfate esters with considerable acceleration over solution reactions. The catalytic proficiencies (defined by the ratio of κcat/KM and rate of the uncatalyzed reaction in solution, κω) vary greatly, ranging from > 1027 for the cognate activity13,14 to ∼ 106 for the promiscuous activity15. The reaction specificities of AP and NPP (characterized by ratios of κcat/KM for cognate and promiscuous substrates in the two enzymes) for phosphate mono- and di-esters differ by up to a remarkable level of 1015 fold.14,16 These significant levels of catalytic specificity and promiscuity are particularly striking in light of the fact that AP and NPP are very similar in their active site features yet have limited sequence identity (8%): as illustrated in Fig.1, both AP and NPP feature a highly conserved bi-metallo zinc active site with the same set of metal ligands (three Asp and three His residues). These characteristics make this pair of enzymes ideal for in-depth comparative analyses, i.e., to understand how they combine the high levels of catalytic proficiency and promiscuity by making use of similar active sites.
Fig. 1.
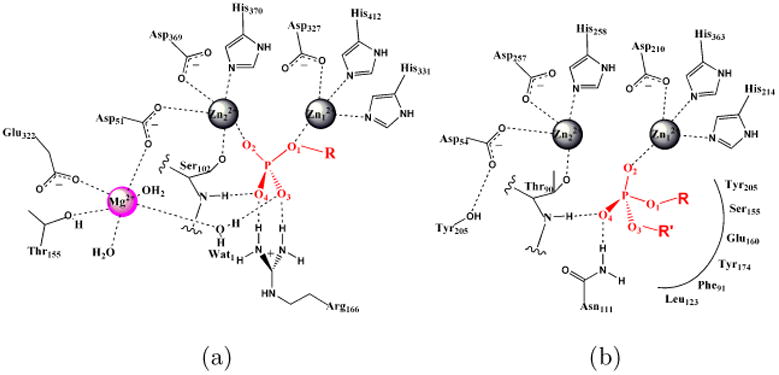
The active sites of Alkaline Phosphatase (AP) and Nucleotide PyrophosPhatase/phosphodiesterase (NPP) are generally similar, with a few distinct differences. (a) E. coli AP active site. (b) Xac NPP active site. The cognate substrates for AP and NPP are phosphate monoesters and diesters, respectively. The labeling scheme of substrate atoms is used throughout the paper. We propose that diesters and monoesters have different binding modes in the active site (see Sect.III B for discussions).
Extensive work has been carried out to characterize the structure and function of AP and NPP. Crystal structures16,17 show that, in spite of the similarities, several differences can be noted between these enzymes. First, the AP active site has additional positively charged motifs, in particular a magnesium ion and Arg166; these are replaced in NPP by charge-neutral residues, Thr205 and Asn111, respectively. The extra positive charges in AP likely help stabilize phosphate monoesters over diesters due to difference in the charge states of these substrates (dianionic vs. monoanionic). Second, the NPP active site is featured with additional hydrophobic residues (e.g., Leu123, Phe91 and nearby residues, see Fig.1), which are expected to help bind diesters more tightly than monoesters. Motivated by these observed differences, systematic analyses over the last few years have helped quantitatively account for a significant fraction of the 1015 fold differential catalytic specificity in AP and NPP:14,16 (1) Arg166 in AP interacts favorably with two negatively charged nonbridging phosphoryl oxygen atoms present in phosphate monoesters but not diesters, giving a preference to monoesters of ∼ 104 fold; (2) the hydrophobic R′ binding pocket of NPP provides ∼ 104 fold preference to diester catalysis; (3) the Mg2+ site in AP contributes through water-mediated hydrogen-bonding interaction with the transferred phosphoryl group, which bears less negative charge in the case of diesters, to favor the monoester reaction by a ∼ 104 fold.
Despite progress, crucial questions remain to be answered for catalysis in AP and its superfamily members. In particular, a fundamental hypothesis regarding catalytic promiscuity in AP/NPP, which was motivated by experimental linear free energy relation (LFER18) and kinetic isotope effect (KIE) data19–23, is that AP and NPP do not alter the nature of phosphoryl transfer TS relative to solution reactions, instead they recognize and stabilize TSs of different nature for cognate and noncognate substrates. This property has been proposed to assist in the evolutionary optimization of promiscuous activities and challenges the traditional notion that an enzyme active site is evolved to stabilize a single type of TS. Recent QM/MM calculations24–26 using the AM1(d)-PhoT method27 as the QM level, however, do not seem to support this model. Although the calculations found that phosphate monoester hydrolysis in AP proceeds via a loose TS24, similar to in aqueous solution, the TS for phosphate diester was found to change from synchronous in solution to very loose in both NPP25 and AP26. The latter is in contrast to conclusions from LFER analysis for phosphate diester hydrolysis in AP22, in which the TS is determined to be synchronous, similar to its solution reference. Nevertheless, citing the previous discussion28 of ambiguity in using LFER data to infer the structure of TS, the authors of Ref.26 proposed a picture for the evolution (and catalytic promiscuity) of the AP superfamily in which the nature of the TS (loose) is maintained for different substrates (e.g., mono- and di-esters)26; this scenario has been established to explain catalytic promiscuity observed for protein phosphatase-129. It should be noted, however, that whether the computational method was sufficiently reliable in the recent QM/MM studies is not clear; for example, the Zn2+-Zn2+ distance was found to vary greatly during the reaction for both mono- and di-ester substrates in AP and NPP24–26, reaching 7.0 Å as compared to the value of ∼4 Å in the crystal structure16,30 and other structural characterizations (EXAFS)31.
To help clarify the situation, we set out to use combined QM/MM potential to systematically investigate the hydrolysis reaction of various cognate/noncognate substrates of AP/NPP in solution and enzymes. In this paper, we focus on the hydrolysis reactions for the same diester substrate studied in previous QM/MM calculations24,25, MpNPP− (Fig.2), and its phosphorothioate analog (MpNPPS−), in solution, two experimentally well-characterized variants of AP (R166S and R166S/E322Y), and the wild type NPP. Since the active sites of AP and NPP are fairly open and readily accessible to solvents (which is what made it possible to carry out LFER studies for these systems), conformational sampling is expected to be crucial. This consideration together with the fairly large size of the bi-metallic zinc catalytic center suggest that an appropriate approach is to use the Self-Consistent-Charge Density-Functional-Tight-Binding (SCC-DFTB)32 as QM in a QM/MM framework. With respect to computational efficiency, SCC-DFTB is comparable to widely used semi-empirical methods such as AM1 and PM333, i.e., it is 2-3 orders of magnitude faster than popular DFT methods. In terms of accuracy, fairly extensive benchmark calculations have indicated that it is particularly reliable for structural properties, while energetics are generally comparable to AM1 and PM3.34–36 For phosphoryl transfer reactions, however, a reaction-specific parameterization based on hydrolysis reactions of model phosphate species, referred to as SCC-DFTBPR,37 appears to be more effective than standard semi-empirical methods and has been found successful in several applications to solution and enzyme systems.38–40
Fig. 2.
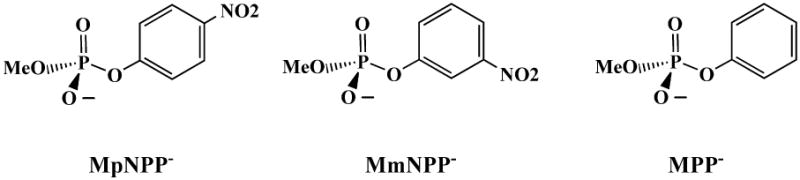
Methyl p-nitrophenyl phosphate (MpNPP−) and its two diester analogs studied in this work.
Here we further test the reliability of SCC-DFTBPR for MpNPP− in different environments (solution, AP and NPP) by comparing results to higher-level QM (QM/MM) calculations as well as available experimental data. A more systematic comparison with LFER and KIE data requires much more extensive calculations and is left as a separate study. Nevertheless, the encouraging benchmark results obtained so far suggest that the SCC-DFTBPR based QM/MM approach can be used to probe the nature and energetics of phosphoryl transfer TS in AP and NPP at a semi-quantitative level. In contrast to recent QM/MM calculations24,25, which found a much looser TS in NPP than in solution, the results here support that the nature of the phosphoryl transfer TS for phosphate diesters is not loosened in neither AP nor NPP relative to solution; in fact, the TS becomes slightly tighter in AP and NPP than in solution, due in part to the geometry of the bimetallic zinc motif. Therefore, our study highlights the importance of using a carefully benchmarked QM/MM model to investigate the nature of phosphoryl transfer TS; moreover, these data provide the first explicit computational support of the hypothesis that the nature of TS for the same substrate is similar in the AP family and in solution.
The paper is organized as follows: in Sect.II we summarize computational methods and simulation setup. In Sect.III, we first present results for the reference solution reactions, and then analysis of the phosphoryl transfer TS for phosphate diesters in several variants of AP and wild type NPP; we also analyze the effect of thio substitution of the diester substrate, which was used experimentally to probe the orientation of the substrate in the active site. Since the Zn2+-Zn2+ distance exhibits rather different behaviors in this and previous QM/MM simulations of AP/NPP24,25, we also explicitly analyze the impact of this fundamental geometrical feature of the bimetallic zinc site on the catalysis. Before concluding in Sect.IV, we summarize the key differences between our and recent QM/MM studies24–26 and also a number of issues that we recommend to examine by future experiments.
II. Computational Methods
A. Diester hydrolysis in solution with the SCC-DFTBPR based implicit solvent model
As an important benchmark and reference, we first study the hydrolysis of MpNPP− and two of its analogs (Fig.2) in solution, which have been thoroughly studied experimentally. To focus on the quality of the QM model rather than other technical details such as QM/MM coupling and sampling, we use the implicit solvent model that we have implemented and parameterized for SCC-DFTBPR.41 In this model, the solute radii are dependent on the charge distribution, which makes it particularly useful for studying solution reactions that involve highly charged species; our previous benchmark calculations suggest that the method has comparable accuracy as the SM6 model42, while being much more efficient (due to the use of SCC-DFTB) and having only a small number of parameters.
The potential energy surface (PES) relevant to the hydrolysis reaction is first explored by adiabatic mapping calculations, in which the reaction coordinates are the P-Olg and P-Onu distances; here hydroxide is the nucleophile, and “Olg” and “Onu” indicate the reactive oxygen in the leaving group and nucleophile, respectively. Each point in the 2D PES is obtained by starting the constrained optimization from several different initial structures and taking the lowest energy value. Following the adiabatic mapping calculations, structures along the approximate reaction path are examined carefully to ensure that the change of geometry is continuous along the path; subsequently, the saddle point is fully optimized by conjugated peak refinement (CPR)43 to obtain more precise TS structure and energy. Finally, frequency calculations are carried out to confirm the nature of the stationary points and to compute the vibrational entropy and zero point energies to obtain approximate activation free energy; although using a harmonic approximation to estimate activation entropy is known to be of limited accuracy, previous studies of phosphate diester hydrolysis found that activation entropy does not differ much between different diesters28. The vibrational frequencies are also used to estimate 18O kinetic isotope effects (KIEs) for MpNPP− as an additional benchmark of the methodology (see Supporting Information).
To correct for intrinsic errors of SCC-DFTBPR energies, we explore corrections based on gas phase single-point energy calculations with both B3LYP/6-311++G** and MP2/6-311++G** at SCC-DFTBPR geometries; the B3LYP level was found to give very similar results to MP2 for simple phosphate hydrolysis reactions37 (however, see below). As discussed in the literature,44 such a simple correction may not always improve the energetics for semi-empirical methods given the errors in geometry; however, our previous tests37,41 indicated that this correction scheme appears useful for SCC-DFTBPR since the method gives fairly reliable structures, even for transition states.
To further facilitate the analysis of sources of errors in both QM and QM/MM calculations, additional analysis for gas-phase/solution proton affinities (PA) for the leaving groups in MpNPP− and its analogs. QM-only calculations are carried out by Gaussian0345; PCM46 and SM642 models are employed to describe solvation effects. To test the accuracy of QM/MM coupling, solution PAs are also calculated using SCC-DFTB/MM based free energy perturbation calculations47.
B. Enzyme Model Setup
For the hydrolytic reaction catalyzed by the AP superfamily members, a two-step mechanism is usually followed,48 in which an oxygen nucleophile (e.g., Ser or Thr) first attacks the phosphorus/sulfur, then a water (hydroxide) replaces the leaving group in a step that is essentially the reverse of the first; for some family members of the superfamily, however, the mechanism can be more complex49. In this work, to understand the catalytic mechanism of AP with phosphate diesters, we investigate the first step of the hydrolysis reaction of MpNPP− in an E. coli AP variant in which Arg166 is mutated to Ser; this is expected to be the rate-limiting step given the experimental leaving group LFER analysis. Experimentally, this mutant was used to avoid inhibition by Pi,22 and it is believed that the mutation does not alter the reaction mechanism of AP since LFERs are similar in the mutant and WT.20,50 Moreover, the chemical step is fully rate-limiting in this mutant. We also study a double mutant, R166S/E322Y AP, which was constructed in recent experimental studies to analyze the contribution(s) from the Mg2+ site in AP. For NPP, we study the wild type enzyme from Xanthomonas axonopodis pv. citri (Xac).
The enzyme models are constructed based on the X-ray structures for the E. coli AP mutant R166S with bound inorganic phosphate at 2.05 Å resolution (PDB code 3CMR30) and Xac NPP with bound Adenosine Mono-Phosphate (AMP) at 2.00 Å resolution (PDB code 2GSU16). The ezyme model for R166S/E322Y AP is constructed based on the crystal structure of E322Y AP (PDB code 3DYC14) by mutating Arg166 to serine. In each case, starting from the PDB structure, the ligand is first “mutated” to the substrate of interest, MpNPP− or MpNPPS−; two possible orientations of the substrates are considered for the AP active site, with the -OMe group oriented towards either the magnesium ion or Ser102 backbone amide (see additional discussions in Sect.III). Hydrogen atoms are added by the HBUILD module51 in CHARMM.52 All basic and acidic amino acids are kept in their physiological protonation states except for Ser102 and Thr90 in AP and NPP, respectively, which are assumed to be the neucleophiles and deprotonated in the reactive complex. Water molecules are added following the standard protocol of superimposing the system with a water droplet of 27 Å radius centered at Zn12+ (see Fig.1 for atomic labels) and removing water molecules within 2.8 Å from any atoms resolved in the crystal structure.53 Protein atoms in the MM region are described by the all-atom CHARMM force field for proteins54 and water molecules are described with the TIP3P model.55 The QM region includes groups most relevant to the reaction: the two zinc ions and their 6 ligands (Asp51, Asp369, His370, Asp327, His412, His331), Ser102 and MpNPP− for R166S AP; for NPP, this includes two zinc ions and their 6 ligands (Asp54, Asp257, His258, Asp210, His363, His214), Thr90 and MpNPP−. Only side chains of protein residues are included in the QM region and link atoms are added between Cα and Cβ atoms. A larger QM region also has been tested for R166S AP which further incorporates the entire magnesium site, including Mg2+, sidechains of Thr155, Glu322 and three ligand water molecules. Comparison of optimized structures using different QM regions indicates fairly similar optimized structures (see Supporting Information for details), thus the smaller QM region is used for the majority of the calculations. The treatment of the QM/MM frontier follows the DIV scheme in CHARMM; previous benchmark calculations have shown that this scheme generally gives reliable results for structure and energetics in QM/MM calculations provided that the MM charge is small near the QM/MM boundary56 Since the Mg2+ near the QM region in AP is treated as a point charge (otherwise the QM region will become substantially larger), to avoid over-polarization of nearby QM groups, a NOE potential is added to the C-O bonds in Asp51, which is coordinated to both Mg2+ and Zn2+. The NOE potential takes the form:
| (1) |
in which Rmin and Rmax set the interval between which the restraining potential is zero; they are taken to be 0 and 1.28 Å, respectively. Kmax is set to be 104κcal/(mol · Å2).
Due to the fairly large size of the QM region (more than 80 atoms) and extensive sampling required for the open active site of AP and NPP, the SCC-DFTBPR method37 is used for PMF calculations. Extensive benchmark calculations and applications indicate that it is comparable to the best semi-empirical method available in the literature for phosphate chemistry.27,57
The generalized solvent boundary potential (GSBP)58,59 is used to treat long range electrostatic interactions in geometry optimizations and MD simulations. The system is partitioned into a 27-Å spherical inner region centered at the Zn1 atom, with the rest in the outer region. Newtonian equations-of-motion are solved for the MD region (within 23 Å), and Langevin equations-of-motion are solved for the buffer regions (23-27 Å) with a temperature bath of 300 K; protein atoms in the buffer region are harmonically constrained with force constants determined from the crystallographic B-factors.60 All bonds involving hydrogen are constrained using the SHAKE algorithm,61 and the time step is set to 1 fs. All water molecules in the inner region are subject to a weak GEO type of restraining potential to keep them inside the inner sphere with the MMFP module of CHARMM. The static field due to outer-region atoms, , is evaluated with the linear Poisson-Boltzmann (PB) equation using a focusing scheme with a coarse cubic grid of 1.2 Å spacing, and a fine grid of 0.4 Å spacing. The reaction field matrix M is evaluated using 400 spherical harmonics. In the PB calculations, the protein dielectric constant of ∊p = 1, the water dielectric constant of ∊ω = 80, and 0.0 M salt concentration are used; the value of ∊p is not expected to make a large difference in this particular case because the active site is already very solvent accessible and the inner/outer boundary is far from the site of interest. The optimized radii of Nina et al.62,63 based on experimental solvation free energies of small molecules as well as the calculated interaction energy with explicit water molecules are adopted to define the solvent-solute dielectric boundary. To be consistent with the GSBP protocol, the extended electrostatic model64 is used to treat the electrostatic interactions among inner region atoms in which interactions beyond 12 Å are treated with multipolar expansions, including the dipolar and quadrupolar terms.
C. Benchmark enzyme calculations based on minimizations and reaction path calculations
To further test the applicability of SCC-DFTBPR/MM to AP and NPP, geometry optimization for the reactant (Michaelis) complex is compared to results from B3LYP65–67/MM calculations. The basis set used in the B3LYP/MM calculations is 6-31G*68, and the calculations are carried out with the QChem69 program interfaced with CHARMM(c36a2 version).70 Due to the rather large size of the QM region and the high cost of ab initio QM/MM calculations, atoms beyond 7 Å away from Zn1 are fixed to their crystal positions in these minimizations (note that these are not fixed in the potential of mean force simulations, see below. Also, test calculations at the SCC-DFTBPR level show that fixing atoms beyond 7 Å from Zn1 in minimizations do not lead to much difference as compared to a fully flexible inner-region calculation within the GSBP framework). The convergence criteria for geometry optimization are that the root-mean-square (RMS) force on mobile atoms is smaller than 0.30κcal/(mol · Å) and the maximum force smaller than 0.45κcal/(mol · Å).
The Minimum Energy Path (MEP) calculations are carried out by one-dimensional adiabatic mapping at both SCC-DFTBPR and B3LYP/6-31G* levels; the reaction coordinate is the antisymmetric stretch involving the breaking and forming P-O bonds (POlg-POnu), and the step size for the adiabatic mapping is 0.2 Å. At the SCC-DFTBPR level, the transition state is further refined using CPR.
D. 1D and 2D Potential of mean force (PMF) simulations
To study the free energy profile of enzyme reactions, PMF simulations have been carried out for R166S AP, R166S/E322Y AP and NPP with MpNPP− and MpNPPS− as the substrates. After the initial minimizations starting from the relevant crystal structure, the enzyme system is slowly heated to 300 K and equilibrated for 100 ps. The reaction coordinate is defined as POlg-POnu. The umbrella sampling approach71 is used to constrain the system along the reaction coordinate by using a force constant of 150 kcal/mol·Å−2. In total, more than 51 windows are used for each PMF and 100 ps simulations are performed for each window. The first 50 ps trajectories are discarded and only the last 50 ps are used for data analysis. Convergence of the PMF is monitored by examining the overlap of reaction coordinate distributions sampled in different windows and by evaluating the effect of leaving out segments of trajectories. The probability distributions are combined together by the weighted histogram analysis method (WHAM)72 to obtain the PMF along the reaction coordinate. The averaged key structural properties for each window are calculated and summarized in Table IV.
Table IV. Calculated key structural properties for the first step of MpNPP− hydrolysis in AP variants and wild type NPP.
| solution | R166S AP | NPP | ||||||
|---|---|---|---|---|---|---|---|---|
| αa | βb | HPc | ||||||
| reactant | TS | reactant | TS | reactant | TS | reactant | TS | |
| P-Olg | 1.67 | 2.23 | 1.65±0.03 | 1.89±0.07 | 1.66±0.03 | 1.86±0.06 | 1.63±0.03 | 1.83±0.06 |
| P-Onu | ∞ | 2.43 | 3.53±0.07 | 2.00±0.09 | 3.83±0.07 | 2.08±0.08 | 3.51±0.06 | 2.03±0.09 |
| RCd | −∞ | -0.20 | -1.88±0.06 | -0.11±0.07 | -2.17±0.06 | -0.22±0.08 | -1.88±0.06 | -0.20±0.07 |
| TCe | ∞ | 4.66 | 5.18±0.09 | 3.89±0.14 | 5.49±0.08 | 3.94±0.13 | 5.14±0.08 | 3.86±0.14 |
| (4.05) | (5.85) | (5.00) | (6.29) | (5.66) | ||||
| Zn2+-Zn2+ | 4.28±0.22 | 3.93±0.18 | 4.21±0.22 | 3.86±0.16 | 4.38±0.21 | 3.92±0.17 | ||
|
| ||||||||
| Cons-3.6f TCe | 4.65±0.09 | 3.88±0.13 | 4.65±0.09 | 3.85±0.11 | ||||
| Cons-4.1f TCe | 5.31±0.09 | 3.97±0.18 | 5.08±0.08 | 3.97±0.16 | ||||
| Cons-4.6f TCe | 5.83±0.10 | 4.08±0.25 | 5.34±0.08 | 4.09±0.19 | ||||
The substrate methyl group points toward the Mg2+ site (the α orientation);
the substrate methyl group points toward the Ser102 backbone (the β orientation);
the substrate methyl group points toward the hydrophobic pocket;
The Reaction coordinate (RC) is defined as the difference between P-Olg and P-Onu;
The Tightness coordinate (TC) is defined as the sum of P-Olg and P-Onu; in parentheses are values from previous QM/MM simulations25.
Zn2+-Zn2+ distance constrained at 3.6, 4.1 and 4.6 Å respectively. The RMS fluctuations are 0.01 Å.
In a separate set of PMF calculations, the Zn2+-Zn2+ distance is constrained to be 3.6, 4.1 and 4.6 Å, respectively, by a strong constraint with a force constant of 2,000 kcal/mol·Å−2, to investigate the impact of this fundamental variable of the bimetallic site on catalysis in AP and NPP. For reference, the Zn2+-Zn2+ distance found in the various crystal structures for AP and NPP is close to be 4.1 Å.
To verify that the 1D PMFs capture the nature of the phosphoryl transfer transition state, we also carry out 2D PMF calculations for the α orientation of MpNPP−. The reaction coordinates are defined as the P-Olg and P-Onu distances, and the range of each distance is similar to that in the 1D PMF calculations. In total, 272 windows are used, and a force constant of 200 kcal/mol·Å−2 is used for all windows; for each window, 100 ps simulations are carried out and only the last 50 ps are used for the subsequent WHAM analysis.
III. Results and Discussion
A. MpNPP− hydrolysis in solution
The hydrolysis of MpNPP− has been studied extensively by experiments and computations. Experimental studies22 determined the activation free energy of 25.7 kcal/mol at 42°C with hydroxide as the nucleophile, and the mechanism is established as concerted with a synchronous TS based on LFER analysis. Several computational work also studied the same reaction by employing various levels of theory. By using B3LYP/6-31+G* and the PCM model, Rosta and coworkers obtained a fairly loose TS with P-Olg and P-Onu as 1.86 and 2.49 Å, respectively.28 By using B3LYP/6-311+G** with the COSMO continuum model on PCM-minimized geometries and a careful treatment of solute configurational entropy, they obtained an activation free energy barrier of 24.4 kcal/mol. In the more recent QM/MM simulations using explicit solvent (TIP3P) and AM1(d)-PhoT27 as QM, López-Canut et al. obtained a free energy barrier of 20.5 kcal/mol; the transition state was featured with the P-Olg and P-Onu distances of 1.81 and 2.23 Å, respectively, somewhat more compact compared with the PCM result.
With our SCC-DFTB(PR)/PB method and charge dependent atomic radii41, the adiabatic map for MpNPP− hydrolysis (Fig. 3a) is qualitatively consistent with previous studies and indicates a synchronous TS with an energy barrier of around 30 kcal/mol. After adding higher level (B3LYP or MP2) single point energy corrections, the general landscape of the adiabatic map does not change (Fig. 3b); the synchronous TS is still preferred with the barrier lowered to around 25 kcal/mol when MP2 corrections are used. After CPR refinement, the fully optimized TS (Fig. 3c) has a P-Olg of 2.23 Å and P-Onu of 2.43 Å; i.e., the P-Olg distance is longer compared with previous theoretical results, while P-Onu is similar. We note, however, the PES is rather flat near the transition state. The free energy barrier by including ZPE and solute configurational entropy is 29.3 kcal/mol at the SCC-DFTBPR level, which is decreased to 24.4 kcal/mol by including gas phase single point energy correction at the MP2/6-311++G** level (Table I); the latter value compares favorably with experimental value.
Fig. 3.
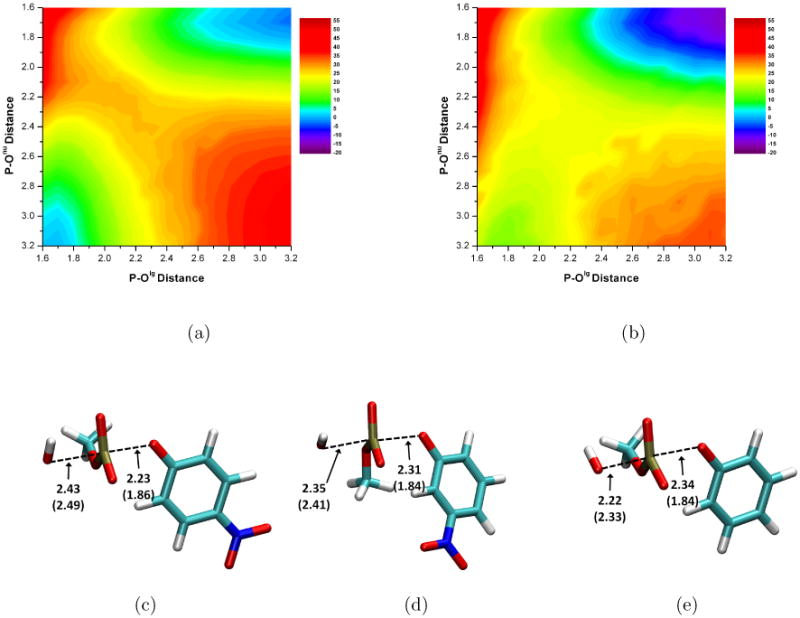
Aqueous hydrolysis of phosphate diesters with hydroxide as the nucleophile. Key distances are labeled in Å and energies are in kcal/mol. (a) Adiabatic mapping results for MpNPP− by SCC-DFTBPR/PB. (b) Adiabatic mapping results for MpNPP− after including single point gas phase correction at the MP2/6-311++G** level. (c-e) Hydrolysis transition state optimized with Conjugare Peak Refinement (CPR) calculations for MpNPP−, MmNPP− and MPP−. Numbers without parentheses are obtained by SCC-DFTBPR/PB; those with parentheses are taken from Ref.28. As shown in the Supporting Information, including the MP2 correction tends to slightly tightens the transition state, especially along P-Olg.
Table I. Energetics for diester hydrolysis reactions in solution from experiments and calculations.
| Diester | pKa | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| MpNPP− | 7.14 | 25.7 | 24.4 | 20.5 | 29.3/21.3/24.4 | ||||
| MmNPP− | 8.35 | 26.3 | 27.3 | 33.3/28.1/27.2 | |||||
| MPP− | 9.95 | 28.6 | 29.9 | 39.8/30.5/30.6 |
Experimental result taken from Ref.22
Calculation result taken from Ref.28
Calculation result taken from Ref.25
For each entry, the numbers are: SCC-DFTBPR/PB, SCC-DFTBPR/PB result including gas-phase B3LYP/6-311++G** single point energy correction, and SCC-DFTBPR/PB result including gas-phase MP2/6-311++G** single point energy correction.
In addition, we study the hydrolysis of two other related diesters (Fig. 2), methyl 3-nitrophenyl phosphate (MmNPP−) and methyl phenyl phosphate(MPP−) with the approach. Experimentally, the trend is that the hydrolysis barrier increases as the pKa of the leaving group increases (Table I)22. This trend has been reproduced by a previous theoretical study28 in which the nature of transition states is found to be synchronous and becomes looser as the pKa of the leaving group decreases; P-Olg ranged from 1.84 to 1.86 Å and P-Onu ranged from 2.33 to 2.49 Å. With our SCC-DFTBPR/PB method, this trend is also qualitatively reproduced, regardless of whether the gas-phase correction at higher level (B3LYP or MP2) is included. At a quantitative level, however, the SCC-DFTBPR/PB barriers are too high and the effects of the substitution are overestimated (see Table I); for example, the barrier difference between MpNPP− and MPP− is only 2.9 kcal/mol according to experiment, but 10.5 kcal/mol at the SCC-DFTBPR/PB level. The discrepancy remains fairly large even with B3LYP corrections, while including the MP2 gas-phase corrections significantly improves the agreement with experimental value. The nature of the TS also becomes somewhat tighter (especially P-Olg, by ∼ 0.2 Å) when MP2 correction is included (see Supporting Information).
To better understand the quantitative differences between SCC-DFTBPR, B3LYP and MP2 results, we examine the relative PAs of the leaving groups in the three phosphate diesters in both gas-phase and solution; gas-phase PAs reflect the intrinsic accuracy of the QM method, while solution PA calculations also examine the accuracy of either the implicit solvent model or QM/MM interactions in explicit solvent simulations73. As shown in Table II, all DFT methods, which include both SCC-DFTB(PR) and B3LYP, have errors much larger than “chemical accuracy” (1 kcal/mol) for the relative gas-phase PAs, especially concerning the effect of introducing the nitro group; by comparison, MP2 does a much better job. The errors in the relative solution PAs follow the same trend as the relative gas-phase PAs, suggesting that errors in the gas-phase PAs are the major source of error; this is confirmed by the observation that computed relative solvation free energies for the leaving groups considered here are in good agreement with experimental values using both SCC-DFTB(PR) and B3LYP based implicit solvent models, with the exception of B3LYP and UAKS radii (see Supporting Information).
Table II. Relative proton affinities (in kcal/mol) for leaving groups in the studied diestersa.
| Diester | Expb | SCC-DFTBPRc | SCC-2ndc | B3LYPd | MP2e |
|---|---|---|---|---|---|
| MpNPP− | 0 | 0 | 0 | 0 | 0 |
| MmNPP− | 6.6 (1.7) | 8.7/9.7 (4.7) | 7.6/8.3 (3.3) [4.9] | 9.1/11.1 (1.1) | 5.5/7.9 |
| MPP− | 21.4 (3.8) | 28.3/30.0 (10.0) | 26.7/27.8 (6.8) [10.1] | 25.3/28.2 (2.2) | 21.2/24.1 |
Since only relative proton affinities (PAs) are of interest, no zero-point energy or thermal corrections has been included. The numbers without parenthesis are gas-phase PAs calculated at gas-phase/solution optimized structures; those with parenthesis are solution PAs. Numbers with bracket are obtained by explicit solvent QM/MM free energy perturbation.
Experimental values for gas-phase PA are taken from ref98. The solution PAs are converted based on experimental pKa differences at 298K99.
The solution geometries are optimized by SCC-PB41 at the corresponding level; “SCC-2nd” indicates the standard second-order SCC-DFTB32.
Gas-phase geometries are optimized with B3LYP/6-311++G(d,p); solution geometries are optimized with PCM/UAKS at the same level of theory.
Gas-phase geometries are optimized with B3LYP/6-311++G(d,p); solution geometries are optimized with PCM/UAKS at the same level of theory. Single point energies are calculated with MP2/6-311++G(d,p).
As additional benchmark for the nature of the TS, 18O KIE calculations for MpNPP− in solution are carried out with the SCC-DFTBPR transition state and harmonic vibrational frequencies. As shown in Table S2, the trends are in qualitative agreement with experimental results74,75 and previous AM1(d)-PhoT and B3LYP results.76 On the other hand, we note that SCC-DFTBPR overestimates the magnitude of the KIEs, especially for the effects associated with the leaving group oxygen and the non-bridging oxygen. This is consistent with the trend discussed above that SCC-DFTBPR predicts a solution TS that is looser as compared to previous theoretical calculations, with most notably a weaker and longer P-Olg bond.
In short, the benchmark calculations for the phosphate diesters and their leaving groups suggest that SCC-DFTBPR can provide fairly reliable structural properties of these species and a semi-quantitative description of energetics and the nature of hydrolysis transition state, especially for relative trends associated with different substituents on the leaving group.
B. First step of MpNPP− hydrolysis in R166S AP
Based on the crystal structure of the AP R166S mutant complexed with inorganic phosphate, the phosphate ligand is “mutated” to MpNPP− by adding necessary functional groups to phosphate oxygen. The leaving 4-nitrophenyl group is added to O1 due to the geometrical requirement of the in-line attack from Ser102 (see Fig. 1a). The methyl group can be added to O3 or O4, which correspond to two different substrate orientations (denoted as α and β orientations, respectively, following the notation of Ref.14). Recent experimental studies14 using a double mutant AP with the Mg2+ site removed and phosphorothioate diesters suggested that the α orientation is preferred over the β orientation. As discussed below (see Sect.III C), however, the interpretation of those elegant experiments may not be as clearcut as presented. Moreover, even if the α orientation is indeed dominant, it is not clear if the discrimination comes from binding or the chemical step. Therefore, it is informative to study both orientations.
The comparison of optimized structures by B3LYP/MM and SCC-DFTBPR/MM shows good agreement between the two levels (Fig.4a). The OSer102-P distance increases from 3.1 Å in the crystal structure to 3.4 (3.3) /3.8 (3.9) Å in B3LYP/MM (SCC-DFTBPR/MM) optimized structure for the α/β orientation, leading to a stable reactant complex. The O2 of the substrate coordinates to one of the zinc ions and O1 with the phenyl group is solvated by water molecules. Interestingly, the slight shift of the substrate position also increases the distance between a Mg2+-bound water (Wat1) and substrate O3 such that a hydrogen bond is formed between Wat1 and the Zn2+-activated Ser102, instead of with an inorganic phosphate oxygen as in the crystal structure (this holds also in MD simulations at the SCC-DFTBPR/MM level; also see discussion below for interactions in the TS). O4 and the nearby Ser102 backbone amide forms the only direct hydrogen bond between the substrate and the enzyme, which is shorter (1.9 Å vs. 3.3 Å) with the substrate in the α orientation than in the β orientation. If this is the only major difference between those two orientations, the binding affinity of MpNPP− to the enzyme is likely stronger with the α orientation than with the β orientation, although a more quantitative estimate remains to be carried out with free energy simulations, which we defer to a future study. Many other hydrogen-bonding distances (e.g., between Wat1 and Ser102, MpNPP− and Ser102 backbone amide) and distances involving the zinc ions (e.g., between Ser102/MpNPP− and the zinc ions) are similar at the two levels of theory (see Fig.4). The Zn2+-Zn2+ distance is generally shorter at the SCC-DFTBPR/MM level (by ∼0.1-0.2 Å) while the distances between Zn and its ligand oxygen are generally longer. Overall, however, the agreement between optimized structures at the two levels of theory is excellent, supporting the use of SCC-DFTBPR/MM.
Fig. 4.
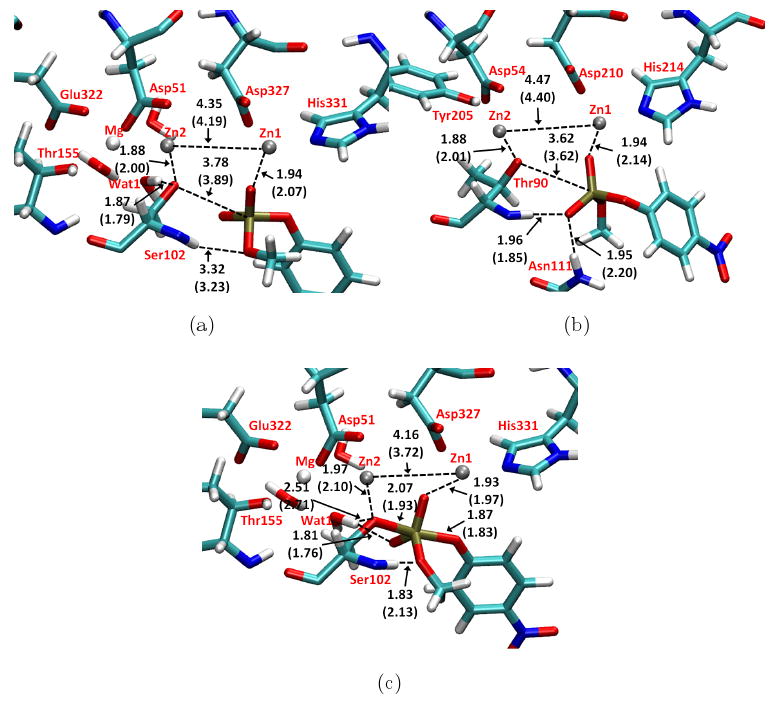
Benchmark calculations for MpNPP− in enzymes. Key distances are labeled in Å. Numbers without parentheses are obtained with B3LYP/6-31G*/MM optimization; those with parentheses are obtained by SCC-DFTBPR/MM optimization. (a) In R166S AP with the substrate methyl group pointing toward Ser102 backbone (the β orientation). (b) In NPP with the substrate methyl group pointing toward the hydrophobic pocket. (c) Comparison of transition state obtained by adiabatic mapping for the β orientation in R166S AP. In (a,c), Asp369, His370 and His412 are omitted for clarity, while in (b), Asp257, His258, His363 are omitted for clarity.
In addition to the structural similarity in optimized reactants, the MEP results (for β orientation) from adiabatic mapping also show good agreement (16.9 vs. 15.7 kcal/mol) between SCC-DFTBPR/MM and B3LYP/6-31G*/MM calculations, which further supports the use of SCC-DFTBPR/MM; the adiabatic mapping and CPR calculations at the SCC-DFTBPR/MM level give similar transition states (see Supporting Information), although the barrier height is slightly lower with fully (CPR) optimized saddle point (see Table III). As shown in Fig.4c, the main differences between SCC-DFTBPR/MM and B3LYP/MM transition states include a shorter Zn2+-Zn2+ distance at the former level, a shorter P-OSer102 bond length and hydrogen-bond distances for the interaction between the substrate and nearby groups (e.g., Ser102 backbone amide and Mg2+-bound Wat1). We note that, in those MEP calculations with SCC-DFTBPR, the Zn2+-Zn2+ distance appears somewhat shorter in the TS for the β orientation than the α orientation (see Supporting Information), although the difference is much smaller in the PMF calculations (see below), again highlighting the importance of sampling protein fluctuations. Nevertheless, there is room to further improve the SCC-DFTBPR method, which may require including complete third-order terms in the SCC-DFTB expansion77 and a more systematic refitting of the P-O repulsive potential78.
Table III.
Barriers and experimental rates for the first step of MpNPP− hydrolysis in AP variants and wild type NPP
| Systema | Substrate | κcat/KM | Expb | α/Rpc | β/Spd |
|---|---|---|---|---|---|
| R166S AP | MpNPP− | 0.48 | 18.0 | 23.4f (13.1g) | 19.6f (12.1g/15.7h) |
| MpNPPS− | 1.1 ×10−3 | 21.6 | 25.5f (15.2g) | 33.4f (20.7g) | |
| R166S/E322Y AP | MpNPP− | 0.24 | 18.4 | 22.6f | >30f |
| MpNPPS− | 3.0 ×10−3 | 21.0 | 19.7f | >40f | |
| NPP | MpNPP− | 2.3 ×102 | 14.3 | 20.2e,f | |
| R166S AP cons-3.6 | MpNPP− | 19.0 | |||
| R166S AP cons-4.1 | MpNPP− | 22.7 | |||
| R166S AP cons-4.6 | MpNPP− | >29 | |||
| NPP cons-3.6 | MpNPP− | 17.0 | |||
| NPP cons-4.1 | MpNPP− | 19.2 | |||
| NPP cons-4.6 | MpNPP− | 24.9 |
In the “cons” simulations, the Zn2+-Zn2+ distance is constrained to be a specific value;
Free energy barrier (kcal/mol) calculated by transition state theory at 300 K based on experimental κcat/KM value;
For MpNPP−, the substrate methyl group points toward the Mg2+ site; for MpNPPS−, it's the Rp enantiomer.
For MpNPP−, the substrate methyl group points toward the Ser102 backbone; for MpNPPS−, it's the Sp enantiomer.
the substrate methyl group points toward the hydrophobic pocket of NPP;
PMF barrier with SCC-DFTBPR/MM;
Barrier from CPR calculations with SCC-DFTBPR/MM;
adiabatic mapping barrier with B3LYP/6-31G*/MM.
For both substrate orientations, the PMF peaks at the reaction coordinate (POlg-POnu) slightly less than 0 Å and then drops in the product region, corresponding to an exothermic reaction (Fig. 5a, 7a). The free energy barriers are 23.4 and 19.6 kcal/mol for the α and β orientations, respectively (see Table III). It is worth mentioning that these barriers correspond to the free energy difference between the TS and the Michaelis complex, i.e., κcat, while experimentally reported values are κcat/KM, which prevents a direct comparison between calculation and experiment. Nevertheless, the measured κcat/KM for R166S AP with MpNPP− corresponds to a free energy barrier of 18.0 kcal/mol, which gives the lower bound for the free energy barrier for the chemical step. Therefore, our calculated barriers for the chemical step are qualitatively consistent with the measured κcat/KM value. The calculations also suggest that the α orientation has a higher barrier for the chemical step. Therefore, for the α orientation to be at least as competitive as the β orientation in terms of κcat/KM, the corresponding binding free energy should be at least 3.8 kcal/mol stronger, which is qualitatively consistent with the above observation of a stronger hydrogen bonding interaction between the enzyme and MpNPP− in the α orientation. Although further binding free energy calculations need to be carried out, the results suggest that the model14 in which the α orientation is the only productive binding mode seems oversimplified (see Sect.III C below for additional discussions).
Fig. 5.
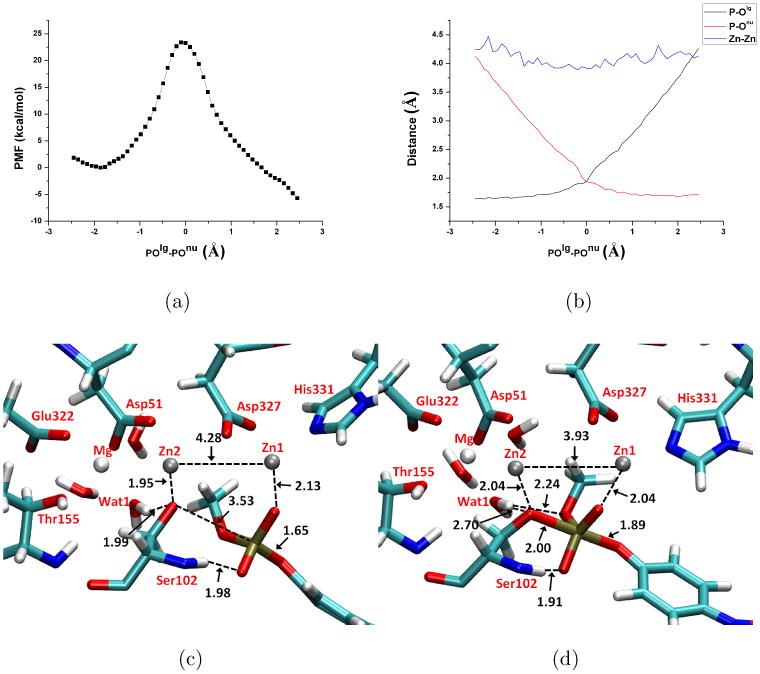
Potential of Mean Force (PMF) calculation results for MpNPP− hydrolysis in R166S AP with the substrate methyl group pointing toward the Mg2+ site (the α orientation). Key distances are labeled in Å and energies are in kcal/mol. (a) PMF along the reaction coordinate (the difference between P-Olg and P-Onu); (b) changes of average key distances along the reaction coordinate; (c) A snapshot for the reactant state, with average key distances labeled. (d) A snapshot for the TS, with average key distances labeled. In (c-d), Asp369, His370 and His412 are omitted for clarity.
Fig. 7.
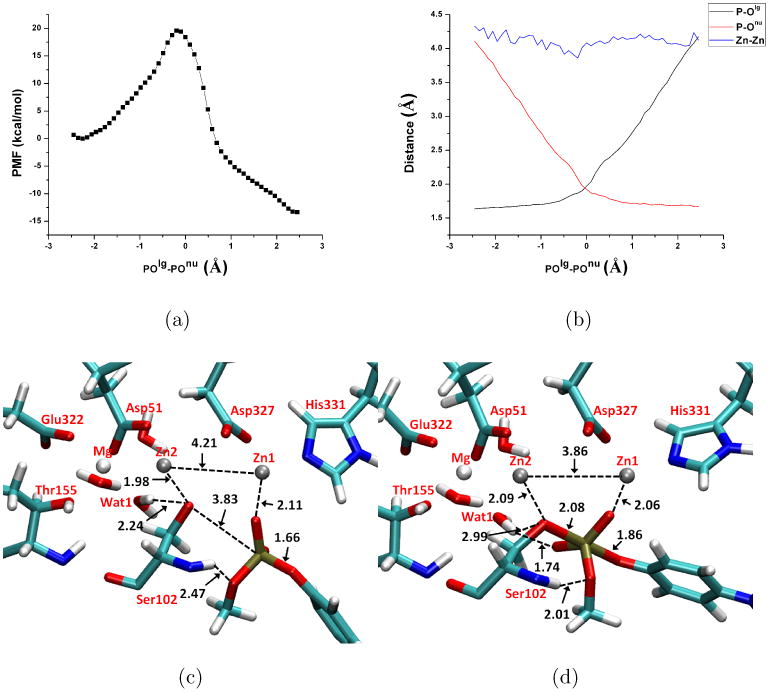
Potential of Mean Force (PMF) calculation results for MpNPP− hydrolysis in R166S AP with the substrate methyl group pointing toward Ser102 backbone (the β orientation). All other format details follow Fig.5.
The key structural properties of the active site are averaged over the trajectory of each window and plotted as functions of the reaction coordinate (Fig. 5b, 7b). The changes of P-Olg and P-Onu clearly show that the concerted pathway with a synchronous TS is operative for both substrate orientations and similar to the reaction in aqueous solution, supporting that AP does not significantly alter the nature of hydrolysis TS for phosphate diesters; this is in qualitative agreement with LFER data for R166S AP and a series of substituted methyl phenyl phosphate diesters22. The nature of the calculated TS is not sensitive to the definition of the 1D reaction coordinate, since the 1D (Fig.5) and 2D (Fig.6) PMF calculations show very consistent results in terms of both structures and energetics. In terms of the tightness coordinate (TC=POlg+POnu), it decreases from 4.66 Å in solution to 3.89 (α) and 3.94 Å (β) in R166S AP (Table IV); this decrease is likely due to the bi-metallic zinc motif in AP, since both MpNPP− and Ser102 are coordinated with Zn2+ ions, which are separated by ∼ 4 Å throughout the reaction. We note that the degree of tightening is likely not as large as the values for TC imply since our calculations appear to overestimate the value of TC for solution reactions as compared to previous calculations25,28.
Fig. 6.
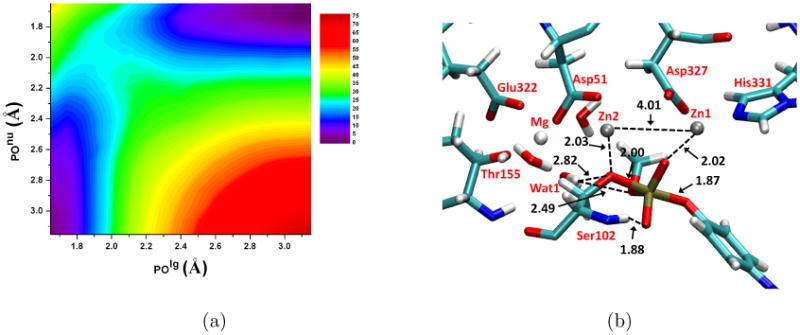
2D Potential of Mean Force (PMF) calculation results for MpNPP− hydrolysis in R166S AP with the substrate methyl group pointing toward the Mg2+ site (the α orientation). Key distances are labeled in Å and energies are in kcal/mol. (a) The 2D PMF along the reaction coordinates; (b) A snapshot for the TS, with average key distances labeled. Asp369, His370 and His412 are omitted for clarity. Note that the 2D PMF results are consistent with the 1D PMF results shown in Fig.5.
We note that recent QM/MM simulation of WT AP with both mono- and di-esters24,26 showed rather large structural changes compared to the crystal structure; for example, the Zn2+-Zn2+ distance increases up to 7 Å, while no such major distortion is observed here (also see discussions below in Sect.III E). In the TS for the β orientation (Fig.7d), Wat1 of the Mg2+ breaks the hydrogen bond with Ser102 and forms a new one with O4 of MpNPP−, which is presumably due to the larger reduction of charge on the Ser102-O than the substrate O4; the average Mulliken charges for Ser102 O and O4 are -0.79 and -0.92, respectively, in the reactant, -0.56 and -0.89, respectively, in the TS. This change of hydrogen-bonding interactions likely helps lower the reaction barrier compared with the α orientation in which Wat1 interacts loosely with both Ser102-O and O3 in the TS (see Fig.5d); the average Mulliken charges for Ser102 O and O3 are -0.79 and -0.32, respectively, in the reactant, -0.50 and -0.40, respectively, in the TS.
Another interesting observation is that the leaving group does not form a direct interaction with any zinc ion in either the reactant state or TS; rather, it is “solvated” by water molecules accessible to the fairly open active site. This binding mode (especially in the TS) is in contrast to that observed for vanadate, a widely used transition state analog for phosphoryl transfers, in the crystal structures for AP-vanadate and NPP-vanadate complexes16,79; these structures suggest a binding mode in which one non-bridging oxygen and the leaving oxygen interact directly with one of the zinc ions. Benchmark calculations suggest that our QM/MM protocol is able to reproduce the binding mode of vanadate in the active site of both AP and NPP, and that SCC-DFTBPR describes the interaction between the di-metallic zinc motif and phosphate diesters in good agreement with B3LYP (see Supporting Information). Moreover, MD simulations starting from the vanadate binding mode with the reaction coordinate constrained to be zero converge to the same binding mode shown in Figs.5-7. Collectively, these results suggest that the binding mode observed in the current work is unlikely an artifact of the computational methodology and indeed energetically favorable for systems studied here. We note that the TS for diesters in AP (and NPP, see below) is rather tight in nature, thus the leaving group oxygen doesn't bear any significant formal charge. Therefore, the binding mode captured in the vanadate structures better reflects the situation for monoesters, which feature a much looser TS in which the leaving group is substantially more charged. Our preliminary calculations for monoesters in AP indeed find tighter interactions between the zinc ion and the leaving group (Hou and Cui, work in progress).
C. Additional analysis of substrate orientation: activity in the double mutant (R166S/E322Y) and thio effects in R166S AP
To further clarify the issue of substrate orientation in AP, we carry out simulation studies to analyze two sets of experiments that were designed to answer the same question. In the first set of experiments, Zalatan and coworkers constructed mutants with the Mg2+ site removed (E322Y, E322A, R166S/E322Y) and measured the catalytic activities for phosphate monoester, phosphate diester and sulphate monoester in these mutants14. Based on the observed large detrimental effects of Mg2+ removal on phosphate monoester and sulphate monoester hydrolysis but negligible effect on phosphate diester hydrolysis, they concluded that the α orientation is preferred over the β orientation (also see the discussion on thio effects below). However, these observations alone do not rule out the possibility that the two orientations are in fact similar in activity in the WT (and R166S) enzyme, which is what we have observed in this study (see Table III). In a mutant where one pathway is significantly perturbed, the other can still provide an alternative route, which may explain the only 2 fold decrease in κcat/KM for R166S/E322Y AP as compared to R166S AP (both with MpNPP− as the substrate). To support this, we explicitly carry out calculations for the double mutants.
As mentioned in Computational Methods, the R166S/E322Y double mutant simulations are prepared based on the crystal structure of E322Y AP14, in which the hydroxyl group of Tyr322 occupies the region corresponding to the Mg2+ site in WT AP and forms a hydrogen bond with Asp51; the bimetallic zinc site is largely unaffected. Based on the comparison of results for the α and β orientations in R166S AP (Figs.5-7), we expect that mutating away the Mg2+ site, which turns off interactions between the Mg2+-bound water and substrate oxygen, will result in a large detrimental effect on the β orientation but a much smaller effect on the α orientation. This is exactly what we observe from the double mutant calculations; as shown in Table III, the reaction barrier is slightly decreased to 22.6 kcal/mol for the α orientation but is increased to be over 30 kcal/mol for the β orientation. These results directly support the important role of the Mg2+ site in reducing the barrier for the β orientation, and by inference, for the hydrolysis of phosphate monoesters, as observed experimentally14. Analysis of structures from PMF calculations also indicates that a water molecule penetrates into the double mutant active site for the β orientation to further stabilize the nucleophile in the reactant state, thus also contributing to the significant increase of the barrier; no such water penetration is observed for the α orientation since the hydrophobic -OMe group in the substrate helps block additional water from the active site. The double mutant calculations also explicitly support that the α orientation is not affected much by the Mg2+ site, in agreement with the experimental observation14 that the activity of phosphate diesters remains largely unperturbed in the Mg2+-site mutants. In short, our model that both α and β orientations are productive binding modes in R166S AP while only α is reactive in the Mg2+-site mutants is consistent with available experimental data.
In the second set of experimental studies, Zalatan and coworkers analyzed the reactivities of phosphorothioate diesters in several variants of AP14. Take MpNPPS− as an example (Fig.8), the key observation was that R166S AP reacts with the Rp enantiomer at least 102 times faster than with the Sp enantiomer, suggesting that the binding mode with the R′ (Me) group toward the Mg2+ site and the sulfur toward the Ser102 backbone amide is dominant; a relevant piece of information here is that previous experiments in the same group established that the sulfur is not placed between the Zn2+ ions15. We note, however, these discussions rely on the assumption that phosphorothioate diesters behave, in terms of hydrogen bonding with active site groups, similarly to phosphate diesters, which may not be as clearcut as commonly believed. For example, NBO charge analysis in both gas phase and solution (see Fig. 8) shows that in MpNPPS− the oxygen bonded with the methyl group is in fact more negatively charged than the sulfur; i.e., it is not obvious that the Rp enantiomer of MpNPPS− reflects the a-orientation of MpNPP−. Therefore, although the experimental observation that removal of the Mg2+ site (R166S/E322Y AP vs. R166S) has a similar impact on the hydrolysis of MpNPPS− and MpNPP− suggests that interactions from the Mg2+ site are similar in the phosphorothioate and phosphate esters, it is not clear if the thio effects can unambiguously infer the binding mode of phosphate diester.
Fig. 8.
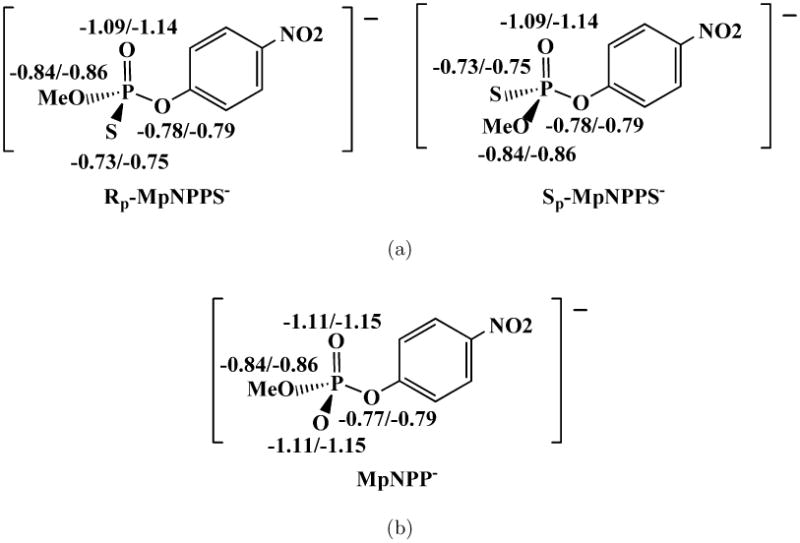
NBO charge analysis for MpNPPS− and MpNPP− in gas phase and solution. Geometries are optimized in gas phase by B3LYP/6-311++G(d,p). Solvation effects are added by PCM with UAKS radii. Numbers before/after slash are gas-phase/solution NBO charges. (a) Enantiomers of MpNPPS−; (b) MpNPP−.
To help better understand the thio effects, we calculate the PMF for MpNPPS− hydrolysis in both R166S AP and R166S/E322Y AP. The results support that in R166S AP, the Rp enantiomer is indeed favored over Sp enantiomer by 7.9 kcal/mol for the chemical step (see Table III), in qualitative agreement with experimental findings. The experimental thio effect (the ratio of rate constant for phosphate ester substrate over that for the phosphorothioate analog) corresponds to a free energy barrier difference of 3.6 kcal/mol, while our calculated value is 2.1-5.9 kcal/mol, depending on whether the α or β orientation for MpNPP− is used as reference; note again, however, the experimental value is based on κcat/KM while our values are based on the chemical step only. One point worth mentioning is that due to the weaker substrate binding following thio substitution, the Solvent Accessible Surface Area (SASA) of the sulfur in MpNPPS− is much larger than that for the corresponding oxygen in MpNPP−, especially for the Sp enantiomer (see Table 2 in Supporting Information); this does not occur at the transition state. The larger SASA provides extra solvent stabilization for the reactant state and probably accounts partially for the much larger thio effects calculated for the Sp enantiomer (13.8 kcal/mol higher in barrier relative to the β orientation of MpNPP−). The PMF profiles for MpNPPS− also peak at where the value of the reaction coordinate is slightly less than 0 while the position of the reactant state is decreased from ∼2 Å in MpNPP− to ∼-2.5 to -3 Å, reflecting the larger substrate size and weaker binding interactions with the active site than MpNPP− (see Supporting Information); the transition state is still synchronous in nature and slightly tighter than MpNPP−.
The effect of removing the Mg2+ site (in R166S/E322Y AP) on the hydrolysis of MpNPPS− is expected to be small for both enantiomers since the interactions between Mg2+-water and either the -OMe or -S− are fairly weak. Indeed, for the Rp enantiomer, the barrier actually decreases in the R166S/E322Y mutant relative to the R166S AP to 19.7 kcal/mol; this value is slightly lower than the experimental κcat/KM value of 21.0 kcal/mol. For the Sp enantiomer, surprisingly, the barrier increases to be over 40 kcal/mol. A closer examination of the simulation snapshots shows that for the reactant state with the Sp enantiomer a solvent water penetrates into the active site and forms a hydrogen bond with the nucleophile (Ser102 oxygen), as illustrated by the comparison of integrated water distribution near the nucleophilic oxygen in Ser102 in the reactant state (see Supporting Information). As mentioned above for the β orientation of MpNPP− in R166S/E322Y AP, which also features a significantly increased barrier (Table III), a similar water penetration is observed as well. The water penetration to Ser102 only happens for these two cases and is reproducible in simulations in which the penetrated water is first deleted and then the system further equilibrated. We note that in R166S AP the active site is already rather open to solvent molecules, thus additional water penetration into the active site is not unexpected when the Mg2+ site is removed; the β orientation and the Sp enantiomer are particularly susceptible to water penetration since they lack the bulky methyl group near Ser102. Nevertheless, water penetration in AP mutants remains an interesting issue that deserves in-depth analysis from future experimental and computational studies.
Considering the results for MpNPP− and those for the Rp enantiomer for MpNPPS− in the two AP variants, our calculations qualitatively reproduced key experimental observations concerning the effects of Mg2+ site removal and thio substitution, further supporting the argument in the last subsection that experimental data so far can not be used to unambiguously determine the orientation of diester substrates in the AP active site. In the broader context, as we mentioned above, the charge distributions for MpNPP− and MpNPPS− bear some nontrivial differences (Fig.8); in addition, the possibilities of water penetrating into the active site for certain orientation of the (thio-substituted) substrate and that different substrate orientations are dominant in different variants of AP (R116S vs. R116/E332Y) further complicate interpretation of the observed thio effects.
D. First step of MpNPP− hydrolysis reaction in NPP
The hydrophobic groove in NPP has been suggested to contribute at least 104-fold to the catalysis of phosphate diester reactions16 by favorable interactions with the extra R′ group in diesters (Fig.1b). Therefore, only one orientation is studied here for MpNPP− in which the methyl group points toward the hydrophobic pocket. Similar to the comparisons made above for AP, SCC-DFTBPR/MM minimizations for MpNPP−-NPP also give similar reactant complex structure to B3LYP/MM calculations (Fig.4b). The OThr90-P distance increases from 3.2 Å in the crystal, which contains AMP as the inhibitor, to 3.6 (3.6) Å at the SCC-DFTBPR/MM (B3LYP/MM) level. The substrate O2 coordinates with Zn1 while O4 forms hydrogen bonds with Asn111 and the backbone amide of Thr90. The optimized Zn2+-Zn2+ distance is 4.47 (4.40) at the B3LYP/MM (SCC-DFTBPR/MM) level. The two hydrogen bonds formed between O4-Asn111 and O4-Thr90-backbone-amide are also in decent agreement at different levels of theory (Fig.4b).
The PMF calculation shows that the free energy profile corresponds to an exothermic process with the barrier located at POlg-POnu ∼-0.20 Å and a barrier height of 20.2 kcal/mol. The measured κcat/KM corresponds to 14.3 kcal/mol at 300 K16 and sets the lower limit for the chemical step barrier. Compared with AP, the calculated barrier for NPP is close to the β orientation but lower than that in the α orientation. Since MpNPP− is the cognate substrate of NPP and therefore expected to bind tighter to NPP than to AP, the calculated barrier implies a higher κcat/KM value for NPP than for AP, which is consistent with experimental observations. In other words, the calculations explicitly support that although diesters are cognate substrates for NPP and promiscuous substrate for AP, the chemical step in NPP is not much accelerated over (R166S) AP.
The changes of P-Olg and P-Onu (Fig. 9b) show that the concerted pathway is also operative for NPP, with a TS similar to that in aqueous solution and AP. For example, the tightness coordinate is 3.86 Å (Table IV), as compared to the values of 3.89(α)/3.94(β) and 4.66 Å, respectively, in R166S AP and solution, respectively. Considering that the tightness coordinate for solution TS seems overestimated by our method compared to previous work25,28, our calculations support the idea motivated by LFER data22 that, instead of altering transition state structure, NPP and AP catalyze phosphoryl transfer reactions by recognizing and stabilizing transition states similar to those in aqueous solution.
Fig. 9.
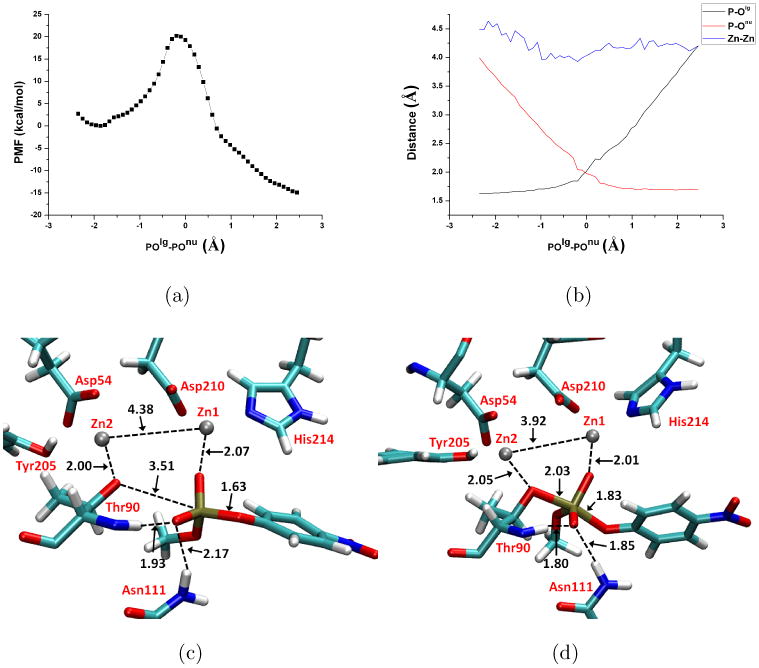
Potential of Mean Force (PMF) calculation results for MpNPP− hydrolysis in NPP with the substrate methyl group pointing toward the hydrophobic core. Other format details follow Fig.5. In (c-d), Asp257, His258, His363 are omitted for clarity.
E. Comparison to recent QM/MM simulations25,26
As just stated, our calculations find that the transition states for diester hydrolysis in AP and NPP are similar and slightly tighter than that in solution. This is in direct contrast to the recent QM/MM studies25,26 which found that the TS in AP/NPP is much looser in nature with the tightness coordinate of 5.66 (NPP)/5.00 (AP) vs. a value of 4.05 in solution. Several pieces of evidence suggest that those calculations are less reliable than our SCC-DFTBPR/MM calculations. First, as noted above for AP, their calculations led to large structural distortions in the bi-metallic zinc motif relative to the crystal structure, while no such distortions occur in our calculations; the same trends hold for NPP calculations, and the loose TS found in previous work25,26 might be a result of the substantially elongated Zn2+-Zn2+ distance. Another example concerns the hydrogen-bond between Asn111 and MpNPP− in NPP, which is observed in the crystal structure (with AMP and vanadate) and throughout our simulations; by contrast, this interaction was broken in the recent QM/MM simulations.25 Second, our calculated barrier heights are consistently higher than the barriers that correspond to experimentally measured κcat/KM values, while this is not the case for recent QM/MM calculations for both NPP25 and AP26. For example, for NPP with the same substrate, their best estimate of the barrier25 was ∼11 kcal/mol, which is even lower than the barrier estimated based on experimental κcat/KM, casting further doubt on the quantitative nature of their result.
What could be the origin for the differences between our and the recent QM/MM calculations25,26? Both SCC-DFTBPR and AM1(d)-PhoT are approximate in nature and parameterized rather specifically for phosphate hydrolysis reactions. For solution reaction, the AM1(d)-PhoT approach gives encouraging results in terms of both energetics and KIEs76, while SCC-DFTBPR, once corrected for gas-phase energies based on MP2, gives good barriers but too loose transition states as reflected by the computed KIE values. In the context of zinc containing enzymes, however, the SCC-DFTBPR approach has been tested with more benchmark calculations, including those discussed here. Indeed, although AM1/PM3 has been used successfully to describe a number of metalloenzymes that catalyze phosphoryl transfers80,81, combining AM1 for zinc and AM1(d)-PhoT for phosphoryl transfers in zinc enzymes has not been carefully tested. Therefore, we suspect that the main cause for the large structural variations in the recent QM/MM simulations25,26 is the use of AM1 for zinc. In this regard, although it is possible that the crystal structure with an inhibitor (e.g., inorganic phosphate) doesn't capture all structural features (e.g., variation in the zinc-zinc distance) of the transition state, the fact that the active site undergoes little change with a transition state analogue (vanadate, see discussions in Sect.III B and also Supporting Information) in both high-resolution crystallography and EXAFS studies31 suggests that large variations in the zinc-zinc distance seen in the recent QM/MM simulations25,26 (including in the Michaelis complexes!) are unlikely realistic. Since the large increase in the zinc-zinc distance occurs in their calculations of several AP and NPP variants25,26, the effect likely cancels out for relative trends; this explains why mutation effects were adequately captured in Ref.26. Finally, we noted that the QM/MM boundary in Refs.25,26 cuts across fairly polar covalent bonds yet the simple single link-atom scheme was used. As emphasized by several researchers56,82–84, extra care needs to be exercised when the QM/MM boundary involves polar bonds. This technical detail likely also contributes to the uncertainty of the results in Refs.25,26.
F. Why is the nature of TS for phosphate diesters in AP and NPP similar to that in solution?
As another way to evaluate the conflicting findings in the current and previous QM/MM studies, we further dissect whether our observation that the nature of TS for phosphate diesters in AP and NPP is similar to that in solution is consistent with other known experimental facts. We do so with the scheme outlined in Fig.11, which is qualitatively similar to that used by Herschlag and co-workers18,22,23.
Fig. 11.
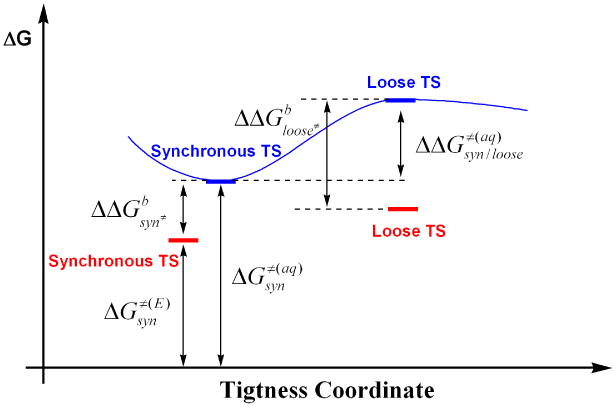
A scheme that illustrates how relative energetics of synchronous and loose transition states in the enzyme (in red) compare to those in solution (in blue). gives the free energy barrier (relative to infinitely separated substrate and nucleophile) in solution/enzyme; gives the binding free energy of a syn/loose TS structure tothe enzyme; is the free energy difference between the synchronous and loose transition state structures in solution. For the enzyme to shift the nature of TS from synchronous to loose, needs to be larger than , which we argue is unlikely for AP and diesters (see text for discussions).
For aryl phosphate diester hydrolysis in solution, the measured reaction barrier, ΔG‡(aq) is ∼26 kcal/mol (e.g., see Table I for MpNPP−); the corresponding barrier in the enzyme, ΔG‡(E), is, for R166S AP, 18.0 kcal/mol (see κcat/KM in Table III). Therefore, the enzyme binds to the TS, which is shown here to be of rather similar synchronous nature in solution and AP/NPP (Table IV), by about 8 kcal/mol .
For the enzyme to shift the nature of TS from synchronous to loose, the driving force needs to be large enough to overcome the binding energy for the synchronous TS plus the energy gap between these two kinds of structures in solution . The latter, although not measurable directly with experiments, can be estimated based on calculations; our calculations shown in Fig.3 give a value ∼ 8 kcal/mol (the “loose” structure is taken to have a tightness coordinate of ∼5.7Å as found for the TS in NPP in previous QM/MM calculations25). In other words, the enzyme needs to bind to the loose TS by more than 16 kcal/mol to make the loose TS more favorable in the enzyme than a synchronous one.
Considering what we know about the activity of AP toward phosphate monoesters, however, we argue that such a strong binding is unlikely for phosphate diesters. For a phosphate monoester related to the diesters studied here, such as pNPP2− (p-nitrophenyl phosphate), the solution barrier is about 32 kcal/mol18 and the barrier in R166S AP is 10.6 kcal/mol85. Since LFER data indicate that the nature of TS is loose in both AP and solution20,85, these results suggest that R166S AP binds a loose TS for monoesters by ∼21 kcal/mol. Since diesters feature less charge and are promiscuous substrates of (R166S) AP, we expect that the binding energy of a loose TS for diesters to R166S AP is substantially lower than 21 kcal/mol. Therefore, we don't expect that R166S AP is able to shift the TS for diesters to be much looser in nature, in agreement with our QM/MM calculations.
For NPP, the diesters are cognate substrates, thus it is conceivable that the active site has been evolved to optimize the catalysis of diester hydrolysis, which might involve modifying the nature of TS relative to solution. However, we note that at least for the diester substrate studied here, the calculated chemical step barrier in NPP (20.2 kcal/mol) is not significantly lower than that in solution (25.7 kcal/mol). Therefore, it is not unreasonable that the nature of TS in NPP is not significantly changed relative to solution and a significant component of rate enhancement over solution (κcat/KM relative to κω) is due to substrate binding.
G. The effects of Zn2+-Zn2+ distance on reaction energetics
Since the bimetallic zinc site is a prevalent catalytic motif86–90, it is of interest to establish what features (e.g., structural vs. electrostatic) are important to the catalytic proficiency. In this work, motivated in part by the fact that the Zn2+-Zn2+ distances behave rather differently in the current and previous QM/MM calculations24,25 of AP and NPP, we examine the effect of this fundamental structural feature on the catalysis in AP and NPP.
Specifically, we design two sets of simulations for R166S AP and NPP with MpNPP− (α orientation only) to study the effects of Zn2+-Zn2+ distance fluctuation and variation. In the first set, we constrain the Zn2+-Zn2+ distance close to the value in crystal structures of AP and NPP (4.1 Å). Due to this constraint, the Zn2+-Zn2+ distance fluctuations in PMF simulations are significantly damped (root-mean-square-fluctuation, rmsf, of ∼0.01 Å) as compared to unconstrained simulations (rmsf∼0.2 Å). As shown in Fig.10a-b, the PMFs for AP and NPP do not exhibit much change, especially in the barrier height, due to the constraint; the nature of the TS (see Supporting Information) also does not change. These observations suggest that fluctuation of the Zn2+-Zn2+ distance during the reaction is not critical to the reaction barrier or the nature of the TS. The significant overlaps of the PMFs also indirectly support the reproducibility and convergence of our PMF simulations.
Fig. 10.
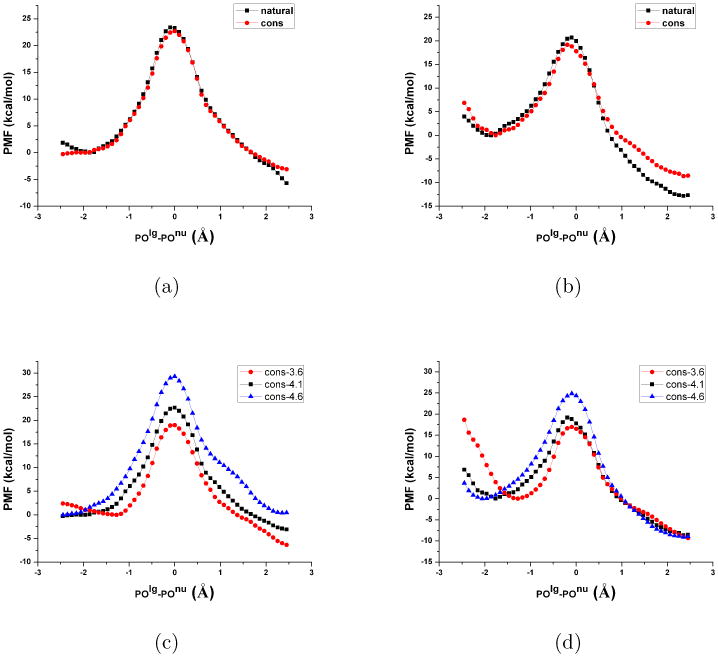
Potential of Mean Force (PMF, in kcal/mol, along the reaction coordinate defined as the difference between P-Olg and P-Onu) comparisons for MpNPP− hydrolysis in R166S AP and NPP with the Zn2+-Zn2+ distance constrained at different values. (a) Between unconstrained and constrained (4.1 Å) simulations for R166S AP. (b) Between unconstrained and constrained (4.1 Å) simulations for NPP. (c) Between constrained simulations at 3.6, 4.1 and 4.6 Å for R166S AP. (d) Between constrained simulations at 3.6, 4.1 and 4.6 Å for NPP. For structural information, see Table IV and Supporting Information.
In the second set of simulations, the Zn2+-Zn2+ distances are constrained at 3.6 and 4.6 Å, respectively, which represent the two extreme values observed in unconstrained simulations. The changes of PMF are similar in AP and NPP (see Fig.10c-d): the reactant state position is shifted to a less negative value and the barrier height is reduced as the Zn2+-Zn2+ distance is decreased from 4.6 to 3.6 Å. In terms of the nature of TS, there is no qualitative change as reflected by the essentially invariant peak position of the PMFs. At the quantitative level, there are variations as reflected by the average tightness coordinate (see Table IV) and other structural parameters (see Supporting Information); for example, the tightness coordinate (TC) increases, as expected, as the Zn2+-Zn2+ distance increases.
In short, these calculations explicitly demonstrate that the Zn2+-Zn2+ distance of the bimetallic zinc site plays an important role in tuning the catalysis. This is not unexpected since the distance between the zinc ions influences the electrostatic properties in the active site, which are crucial to the phosphoryl transfers91. Nevertheless, the results clearly underlines the importance of reproducing geometrical properties of a bimetallic site for a meaningful analysis of its catalytic properties.
H. Issues worthwhile investigating with future experiments
The key objective of this work is to characterize the nature of the hydrolysis TS of phosphate diesters in AP and NPP so as to evaluate different hypotheses22,26 regarding the catalytic promiscuity in these enzymes. To evaluate the main findings of this work, we propose that the following experimental studies are worthwhile.
First, unlike the recent QM/MM simulations25,26, our calculations suggest that the nature of diester hydrolysis TS is largely similar in AP, NPP and solution. Along this line, LFER and KIE studies for diester hydrolysis in NPP will be highly informative.
Second, our calculations find that the leaving group does not interact strongly with the zinc ion in either the reactant or TS for diester hydrolysis in AP/NPP. This is rather unexpected considering the crystal structures of vanadate-AP/NPP complexes16,79 and therefore worth further investigations. Note that this result does not suggest that the second zinc ion does not play an essential role in catalysis since it coordinates with the bridging oxygen. The leaving group is stabilized by active site solvent molecules, suggesting that the dependence of the catalytic rate with respect to the substitution of the leaving group, including both chemical and isotope substitutions, should be close to that in solution.
We have extensively discussed in Sect.III C the issue of different binding orientations of the substrate and relation of current calculations with available experimental studies. As highlighted by the NBO charges shown in Fig.8, one complicating factor for the interpretation of thiol experiments is that phosphorothioate and phosphate esters have rather different charge distributions; in MpNPPS− the oxygen bonded with the methyl group is in fact more negatively charged than the sulfur. Therefore, it will be valuable to explore the reactivity of thiol substrates with both well-defined stereochemistry and relative charge distributions closer to the phosphate esters, such as by replacing both O3 and O4 in MpNPP by sulfur.
Finally, as alluded to in Sect.III G, the metal-metal distance appears to be essential to both the barrier height and the nature of the transition state; the barrier is higher and the nature of TS looser with a longer metal-metal distance. This can be tested by substituting the zinc ions with other metals of different size (e.g., replacing Zn2+ by Co2+) and performing kinetic and LFER analyses. Along this line, analysis of TS nature with synthetic analogs of di-metallic zinc motifs92,93 will be highly informative, since the structure of such artificial catalysts can be better controlled and monitored.
IV. Concluding Remarks
In this work, we have studied the hydrolysis of MpNPP− and its several analogs in solution, two experimentally well characterized variants of AP (R166S and R166S/E332Y) and wild type NPP using SCC-DFTBPR/MM simulations. The main goal is to investigate whether the nature of phosphoryl transfer transition state for the same substrate is significantly different in these enzymes and in solution, a question that has a direct implication to the remarkable catalytic promiscuity exhibited by members of the AP superfamily.
Overall, our results are consistent with available experimental observations. In solution, we show that our calculations are able to capture trends in the hydrolysis barrier for MpNPP− and its two analogs, and the reaction proceeds through a synchronous TS, consistent with expectation based on experimental LFER data. For several variants of AP, our simulations support that the nature of TS is not perturbed significantly relative to solution, with a small degree of tightening due presumably to the interaction with the bi-metallic zinc motif; these are also in qualitative agreement with LFER data for AP variants. Therefore, our calculations support the picture that although the native function of AP is to catalyze the hydrolysis of phosphate monoesters through a loose transition state, its active site accommodates the tighter transition state for diesters. Such active site “plasticity” has been proposed to be related to the catalytic promiscuity of AP. Our analysis (Fig.11) of the free energy surfaces for phosphate diester hydrolysis in solution and AP/NPP supports a simple interpretation of such functional plasticity: the binding of AP to diester substrates is simply not strong enough, presumably due to their lower charge compared to monoesters, to significantly shift the nature of the transition state from synchronous to loose.
For NPP, for which diesters are cognate substrates, our calculations also do not support any major change in the nature of TS relative to solution, in contrast to the recent QM/MM calculations25. Since both structural features of the active site and energetics from our calculations are in better agreement with available experimental data, we expect that the nature of TS from the current work is more realistic. The lack of any significant change in the nature of TS relative to solution is not unexpected considering that the calculated chemical step barrier in NPP is not significantly lower than that in solution. Nevertheless, we hope the current work will stimulate additional LFER studies for NPP to further confirm the nature of TS.
The calculations also reveal several features and underlying complexity of AP catalysis not thoroughly recognized by previous work. For example, concerning the orientation of a diester substrate in the AP active site, our calculations for two variants of AP and two diester substrates collectively indicate that the experimental data alone can't be used to unambiguously show that a single orientation (α) is the only reactive binding mode. In fact, we find that the β orientation with the substrate methyl group pointing toward the Ser102 backbone amide has a reaction barrier lower than that for the α orientation, which has the substrate methyl group pointing toward the Mg2+ site; however, it is possible that the binding free energy for the α orientation is larger to make the overall free energy profile at least comparable to the β orientation. We also argue that the thio-substitution experiments are not always straightforward to interpret, because there is nontrivial differences in the charge distributions for phosphorothioate and phosphate esters; the possibilities of water penetrating into the active site for certain orientation of the (thio-substituted) substrate and that different substrate orientations dominate in different variants of AP (R116S vs. R116/E332Y) further compromise the clarity of interpretation of thio effects. Finally, we discuss results supporting that the Zn2+-Zn2+ distance plays a significant role in modulating the energetics, especially barrier, of phosphoryl transfer in AP and NPP. This result can be probed experimentally by metal substitution and underlines the importance of reproducing geometrical properties of a bimetallic site for a meaningful computational analysis of its catalytic properties.
For a more thorough understanding of catalytic promiscuity and functional evolution of the AP superfamily, it is crucial to carry out similar systematic benchmark and analyses for monoester hydrolysis in solution and AP family enzymes. Since phosphate monoesters bear higher charges than diesters, and that SCC-DFTBPR has been developed based mainly on diesters, it is likely that further improvements of the computational methodology are needed77,78. Once validated for AP and NPP, the computational approach coupled with other methodological advances94–97 is potentially applicable in the prediction and rational design of catalytic promiscuity in other enzyme families.
Supplementary Material
Acknowledgments
We acknowledge stimulating discussions with Professor D. Herschlag and Drs. J. Lassila, L. D. Andrews and J. Zalatan and their critical reading of the manuscript. This work is supported by NIH grant R01-GM084028. Computational resources from the National Center for Supercomputing Applications at the University of Illinois and the Centre for High Throughput Computing (CHTC) at UW-Madison are greatly appreciated; computations are also supported in part by National Science Foundation through a major instrumentation grant (CHE-0840494).
Footnotes
Supporting Information: Additional calculation results and discussions on the following subjects are included: additional benchmarks in both gas-phase (active site cluster model), solution (implicit solvent, kinetic isotope effects) and enzyme active sites (AP bound to inorganic phosphate, vanadate or different binding modes of MpNPP−), additional results for the double mutants, with thio-substituted MpNPP− and constrained zinc-zinc distance. The complete reference for Refs.45, 54, 69, 70 are also included. These materials are available free of charge from http://pubs.acs.org.
References
- 1.O'Brien PJ, Herschlag D. Chemistry & Biology. 1999;6:R91–R105. doi: 10.1016/S1074-5521(99)80033-7. [DOI] [PubMed] [Google Scholar]
- 2.Copley SD. Curr Opin Chem Biol. 2003;7:265–272. doi: 10.1016/s1367-5931(03)00032-2. [DOI] [PubMed] [Google Scholar]
- 3.Schmidt DMZ, Mundorff EC, Dojka M, Bermudez E, Ness JE, Govindarajan S, Babbitt PC, Minshull J, Gerlt JA. Biochem. 2003;42:8387–8393. doi: 10.1021/bi034769a. [DOI] [PubMed] [Google Scholar]
- 4.Zalatan JG, Herschlag D. Nat Chem Biol. 2009;5:516–520. doi: 10.1038/nchembio0809-516. [DOI] [PubMed] [Google Scholar]
- 5.Jonas S, Hollfelder F. Pure & Appl Chem. 2009;81:731–742. [Google Scholar]
- 6.Jensen RA. Annu Rev Microbio. 1976;30:409–425. doi: 10.1146/annurev.mi.30.100176.002205. [DOI] [PubMed] [Google Scholar]
- 7.Aharoni A, Gaidukov L, Khersonsky O, Gould SM, Roodveldt C, Tawfik DS. Nat Genet. 2005;37:73–76. doi: 10.1038/ng1482. [DOI] [PubMed] [Google Scholar]
- 8.Khersonsky O, Roodveldt C, Tawfik DS. Curr Opin Chem Biol. 2006;10:498–508. doi: 10.1016/j.cbpa.2006.08.011. [DOI] [PubMed] [Google Scholar]
- 9.Khersonsky O, Tawfik DS. Annu Rev Biochem. 2010;79:471–505. doi: 10.1146/annurev-biochem-030409-143718. [DOI] [PubMed] [Google Scholar]
- 10.O'Brien P, Herschlag D. J Am Chem Soc. 1998;120:12369–12370. [Google Scholar]
- 11.O'Brien P, Herschlag D. Biochem. 2001;40:5691–5699. doi: 10.1021/bi0028892. [DOI] [PubMed] [Google Scholar]
- 12.van Loo B, Jonas S, Babtie AC, Benjdia A, Berteau O, Hyvönen M, Hollfelder F. Proc Nat Acad Sci USA. 2010;107:2740–2745. doi: 10.1073/pnas.0903951107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lad C, Williams NH, Wolfenden R. Proc Natl Acad Sci USA. 2003;100:5607–5610. doi: 10.1073/pnas.0631607100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zalatan J, Fenn A, Herschlag D. J Mol Biol. 2008;384:1174–1189. doi: 10.1016/j.jmb.2008.09.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lassila J, Herschlag D. Biochem. 2008;47:12853–12859. doi: 10.1021/bi801488c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zalatan J, Fenn T, Brunger A, Herschlag D. Biochem. 2006;45:9788–9803. doi: 10.1021/bi060847t. [DOI] [PubMed] [Google Scholar]
- 17.Stec B, Holtz K, Kantrowitz E. J Mol Biol. 2000;299:1303–1311. doi: 10.1006/jmbi.2000.3799. [DOI] [PubMed] [Google Scholar]
- 18.Lassila JK, Zalatan JG, Herschlag D. Annu Rev Biochem. 2011;80:669–702. doi: 10.1146/annurev-biochem-060409-092741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hollfelder F, Herschlag D. Biochem. 1995;38:12255–12264. doi: 10.1021/bi00038a021. [DOI] [PubMed] [Google Scholar]
- 20.O'Brien P, Herschlag D. J Am Chem Soc. 1999;121:11022–11023. [Google Scholar]
- 21.Nikolic-Hughes I, Rees D, Herschlag D. J Am Chem Soc. 2004;126:11814–11819. doi: 10.1021/ja0480421. [DOI] [PubMed] [Google Scholar]
- 22.Zalatan J, Herschlag D. J Am Chem Soc. 2006;128:1293–1303. doi: 10.1021/ja056528r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zalatan J, Catrina I, Mitchell R, Grzyska P, O'Brien P, Herschlag D. J Am Chem Soc. 2007;129:9789–9798. doi: 10.1021/ja072196+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.López-Canut V, Marti S, Bertrán J, Moliner V, Tuñón I. J Phys Chem B. 2009;113:7816–7824. doi: 10.1021/jp901444g. [DOI] [PubMed] [Google Scholar]
- 25.López-Canut V, Roca M, Bertrán J, Moliner V, Tuñón I. J Am Chem Soc. 2010;132:6955–6963. doi: 10.1021/ja908391v. [DOI] [PubMed] [Google Scholar]
- 26.López-Canut V, Roca M, Bertrán J, Moliner V, Tuñón I. J Am Chem Soc. 2011;133:12050–12062. doi: 10.1021/ja2017575. [DOI] [PubMed] [Google Scholar]
- 27.Nam K, Cui Q, Gao J, York D. J Chem Theory Comput. 2007;3:486–504. doi: 10.1021/ct6002466. [DOI] [PubMed] [Google Scholar]
- 28.Rosta E, Kamerlin SCL, Warshel A. Biochemistry. 2008;47:3725–3735. doi: 10.1021/bi702106m. [DOI] [PubMed] [Google Scholar]
- 29.McWhirter C, Lund EA, Tanifum EA, Feng G, Sheikh QI, Hengge AC, Williams NH. J Am Chem Soc. 2008;130:13673–13682. doi: 10.1021/ja803612z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.O'Brien P, Lassila J, Fenn T, Zalatan J, Herschlag D. Biochem. 2008;47:7663–7672. doi: 10.1021/bi800545n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bobyr E, Lassila JK, Wiersma-Koch HI, Fenn TD, Lee JJ, Nikolic-Hughes I, Hodgson KO, Rees DC, Hedman B, Herschlag D. J Mol Biol. 2011 doi: 10.1016/j.jmb.2011.10.040. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Elstner M, Porezag D, Jungnickel G, Elsner J, Haugk M, Frauenheim T, Suhai S, Seifert G. Phys Rev B. 1998;58:7260–7268. [Google Scholar]
- 33.Thiel W. Adv Chem Phys. 1996;93:703–757. [Google Scholar]
- 34.Kruger T, Elstner M, Schiffels P, Frauenheim T. J Chem Phys. 2005;122:114110. doi: 10.1063/1.1871913. [DOI] [PubMed] [Google Scholar]
- 35.Sattelmeyer KW, Tirado-Rives J, Jorgensen W. J Phys Chem A. 2006;110:13551–13559. doi: 10.1021/jp064544k. [DOI] [PubMed] [Google Scholar]
- 36.Otte N, Scholten M, Thiel W. J Phys Chem A. 2007;111:5751–5755. doi: 10.1021/jp0700130. [DOI] [PubMed] [Google Scholar]
- 37.Yang Y, Yu H, York D, Elstner M, Cui Q. J Chem Theo Comp. 2008;4:2067–2084. doi: 10.1021/ct800330d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Yang Y, Yu H, Cui Q. J Mol Biol. 2008;381:1407–1420. doi: 10.1016/j.jmb.2008.06.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Yang Y, Cui Q. J Phys Chem A. 2009;113:12439–12446. doi: 10.1021/jp902949f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Yang Y, Cui Q. J Phys Chem B. 2009;113:4930–4933. doi: 10.1021/jp810755p. NIHMS:103392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hou GH, Zhu X, Cui Q. J Chem Theo Comp. 2010;6:2303–2314. doi: 10.1021/ct1001818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kelly CP, Cramer CJ, Truhlar DG. J Chem Theory Comput. 2005;1:1133–1152. doi: 10.1021/ct050164b. [DOI] [PubMed] [Google Scholar]
- 43.Fischer S, Karplus M. Chem Phys Lett. 1992;194:511–527. [Google Scholar]
- 44.Cui Q, Karplus M. J Phys Chem B. 2002;106:1768–1798. [Google Scholar]
- 45.Frisch MJ, et al. Gaussian 03. 2003 [Google Scholar]
- 46.Miertus S, Tomasi J. Chem Phys. 1982;65:239–245. [Google Scholar]
- 47.Li GH, Cui Q. J Phys Chem B. 2003;107:14521–14528. [Google Scholar]
- 48.Coleman J. Annu Rev Biophys Biomol Struct. 1992;21:441–483. doi: 10.1146/annurev.bb.21.060192.002301. [DOI] [PubMed] [Google Scholar]
- 49.Jonas S, van Loo B, Hyvönen M, Hollfelder F. J Mol Biol. 2008;384:120–136. doi: 10.1016/j.jmb.2008.08.072. [DOI] [PubMed] [Google Scholar]
- 50.Holtz KM, Catrina IE, Hengge AC, Kantrowitz ER. Biochemistry. 2000;39:9451–9458. doi: 10.1021/bi000899x. [DOI] [PubMed] [Google Scholar]
- 51.Brunger A, Karplus M. Protein Struct Funct Genet. 1988;4:148–156. doi: 10.1002/prot.340040208. [DOI] [PubMed] [Google Scholar]
- 52.Boorks B, Bruccoleri R, Olafson B, States D, Swaminathan S, Karplus M. J Comput Chem. 1983;4:187–217. [Google Scholar]
- 53.Boorks C, Karplus M. J Chem Phys. 1983;79:6312–6325. [Google Scholar]
- 54.MacKerell A, et al. J Chem Phys. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 55.Jorgensen W, Chandrasekhar J, Madura J, Impey R, Klein M. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 56.Konig P, Hoffmann M, Frauenheim T, Cui Q. J Phys Chem B. 2005;109:9082–9095. doi: 10.1021/jp0442347. [DOI] [PubMed] [Google Scholar]
- 57.Arantes G, Loos M. Phys Chem Chem Phys. 2006;8:347–353. doi: 10.1039/b511805k. [DOI] [PubMed] [Google Scholar]
- 58.Im W, Bernèche S, Roux B. J Chem Phys. 2001;114:2924–2937. [Google Scholar]
- 59.Schaefer P, Riccardi D, Cui Q. J Chem Phys. 2005;123:014905. doi: 10.1063/1.1940047. [DOI] [PubMed] [Google Scholar]
- 60.Brooks C, Karplus M. J Mol Biol. 1989;208:159–181. doi: 10.1016/0022-2836(89)90093-4. [DOI] [PubMed] [Google Scholar]
- 61.Rychaert J, Ciccotti G, Berendsen H. J Comput Phys. 1977;23:327–341. [Google Scholar]
- 62.Nina M, Beglov D, Roux D. J Phys Chem B. 1997;101:5239–5248. [Google Scholar]
- 63.Nina M, Im W, Roux D. Biophys Chem. 1999;78:89–96. doi: 10.1016/s0301-4622(98)00236-1. [DOI] [PubMed] [Google Scholar]
- 64.Steinbach P, Brooks B. J Comput Chem. 1994;15:667–683. [Google Scholar]
- 65.Becke A. Phys Rev A. 1988;38:3098–3100. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- 66.Becke A. J Chem Phys. 1993;98:5648–5652. [Google Scholar]
- 67.Lee C, Yang W, Parr R. Phys Rev B. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 68.Petersson G, Bennett A, Tensfeldt T, Allaham M, Shirley W, Mantzaris J. J Chem Phys. 1988;89:2193–2218. [Google Scholar]
- 69.Shao Y, et al. Phys Chem Chem Phys. 2006;27:3172–3191. doi: 10.1039/b517914a. [DOI] [PubMed] [Google Scholar]
- 70.Brooks BR, et al. J Comp Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Torrie GM, Valleau JP. Journal of Computational Physics. 1977;23:187–199. [Google Scholar]
- 72.Kumar S, Bouzida D, Swendsen RH, Kollman PA, Rosenberg JM. Journal of Computational Chemistry. 1992;13:1011–1021. [Google Scholar]
- 73.Riccardi D, Schaefer P, Cui Q. J Phys Chem B. 2005;109:17715–17733. doi: 10.1021/jp0517192. [DOI] [PubMed] [Google Scholar]
- 74.Hengge AC, Tobin AE, Cleland WW. J Am Chem Soc. 1995;117:5919–5926. [Google Scholar]
- 75.Harris ME, Cassano AG, Anderson VE. J Am Chem Soc. 2002;124:10964–10965. doi: 10.1021/ja020823j. [DOI] [PubMed] [Google Scholar]
- 76.Tunon I, Lopez-Canut V, Ruiz-Pernia J, Ferrer S, Moliner V. J Chem Theo Comp. 2009;5:439–442. doi: 10.1021/ct800470f. [DOI] [PubMed] [Google Scholar]
- 77.Gaus M, Cui Q, Elstner M. J Chem Theo Comp. 2011;7:931–948. doi: 10.1021/ct100684s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Gaus M, Chou CP, Witek H, Elstner M. J Phys Chem A. 2009;113:11866–11881. doi: 10.1021/jp902973m. [DOI] [PubMed] [Google Scholar]
- 79.Holtz KM, Stec B, Kantrowitz ER. J Biol Chem. 1999;274:8351–8354. doi: 10.1074/jbc.274.13.8351. [DOI] [PubMed] [Google Scholar]
- 80.Wong KY, Gao JL. Biochem. 2007;46:13352–13369. doi: 10.1021/bi700460c. [DOI] [PubMed] [Google Scholar]
- 81.Wong KY, Gao JL. FEBS J. 2011;278:2579–2595. doi: 10.1111/j.1742-4658.2011.08187.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Das D, Eurenius KP, Billings EM, Sherwood P, Chatfield DC, Hodoscek M, Brooks BR. J Chem Phys. 2002;117:10534–10547. [Google Scholar]
- 83.Gao JL, Ma SH, Major DT, Nam K, Pu JZ, Truhlar DG. Chem Rev. 2006;106:3188–3209. doi: 10.1021/cr050293k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Senn HM, Thiel W. Angew Chem Int Ed. 2009;48:1198–1229. doi: 10.1002/anie.200802019. [DOI] [PubMed] [Google Scholar]
- 85.O'Brie P, Herschlag D. Biochem. 2002;41:3207–3225. doi: 10.1021/bi012166y. [DOI] [PubMed] [Google Scholar]
- 86.Kim EE, Wyckoff HW. J Mol Biol. 1991;218:449–464. doi: 10.1016/0022-2836(91)90724-k. [DOI] [PubMed] [Google Scholar]
- 87.Strater N, Lipscomb WN, Klabunde T, Krebs B. Angew Chem Int Ed. 1996;35:2024–2055. [Google Scholar]
- 88.Steitz TA, Steitz JA. Proc Natl Acad Sci USA. 1993;90:6498–6502. doi: 10.1073/pnas.90.14.6498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Tesmer JJG, Sunahara RK, Johnson RA, Gosselin G, Gilman AG, Sprang SR. Science. 1999;285:756–760. doi: 10.1126/science.285.5428.756. [DOI] [PubMed] [Google Scholar]
- 90.Jedrzejas MJ, Setlow P. Chem Rev. 2001;101:607–618. doi: 10.1021/cr000253a. [DOI] [PubMed] [Google Scholar]
- 91.Nikolic-Hughes I, O'Brien P, Herschlag D. J Am Chem Soc. 2005;127:9314–9315. doi: 10.1021/ja051603j. [DOI] [PubMed] [Google Scholar]
- 92.Gao H, Ke Z, DeYonker NJ, Wang J, Xu H, Mao Z, Phillips DL, Zhao C. J Am Chem Soc. 2011;133:2904–2915. doi: 10.1021/ja106456u. [DOI] [PubMed] [Google Scholar]
- 93.Fan YB, Gao YQ. Acta Phys Chim Sinica. 2010;26:1034–1042. [Google Scholar]
- 94.Hermann JC, Ghanem E, Li Y, Raushel FM, Irwin JJ, Shoichet BK. J Am Chem Soc. 2006;128:15882–15891. doi: 10.1021/ja065860f. [DOI] [PubMed] [Google Scholar]
- 95.Hermann JC, Marti-Arbona R, Fedorov AA, Fedorov E, Almo SC, Shoichet BK, Raushel FM. Nature. 2007;448:775–779. doi: 10.1038/nature05981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Toscano MD, Woycechowsky KJ, Hilvert D. Angew Chem Int Ed. 2007;46:3212–3236. doi: 10.1002/anie.200604205. [DOI] [PubMed] [Google Scholar]
- 97.Jiang L, Althoff EA, Clemente FR, Doyle L, Rothlisberger D, Zanghellini A, Gallaher JL, Betker JL, Tanaka F, Barbas CF, Hilvert D, Houk KN, Stoddard BL, Baker D. Science. 2008;319:1387–1391. doi: 10.1126/science.1152692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Fujio M, Mciver RT, Taft RW. J Am Chem Soc. 1981;103:4017–4029. [Google Scholar]
- 99.Lide DR, editor. CRC Handbook Chemistry and Physics. 85. CRC Press: 2005. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



