Abstract
The acquisition of mammalian endothermy is poorly constrained both phylogenetically and temporally. Here, we inferred the resting metabolic rates (RMRs) and the thermometabolic regimes (endothermy or ectothermy) of a sample of eight extinct synapsids using palaeohistology, phylogenetic eigenvector maps (PEMs), and a sample of 17 extant tetrapods of known RMR (quantified using respirometry). We inferred high RMR values and an endothermic metabolism for the anomodonts (Lystrosaurus sp., Oudenodon bainii) and low RMR values and an ectothermic metabolism for Clepsydrops collettii, Dimetrodon sp., Edaphosaurus boanerges, Mycterosaurus sp., Ophiacodon uniformis and Sphenacodon sp. A maximum-likelihood ancestral states reconstruction of RMRs performed using the values inferred for extinct synapsids, and the values measured using respirometry in extant tetrapods, shows that the nodes Anomodontia and Mammalia were primitively endotherms. Finally, we performed a parsimony optimization of the presence of endothermy using the results obtained in the present study and those obtained in previous studies that used PEMs. For this, we assigned to each extinct taxon a thermometabolic regime (ectothermy or endothermy) depending on whether the inferred values were significantly higher, lower or not significantly different from the RMR value separating ectotherms from endotherms (1.5 ml O2 h−1 g−0.67). According to this optimization, endothermy arose independently in Archosauromorpha, Sauropterygia and Therapsida.
This article is part of the theme issue ‘Vertebrate palaeophysiology’.
Keywords: endothermy, synapsids, quantitative palaeohistology, palaeophysiology
1. Introduction
One of the greatest challenges of current research in palaeobiology is the inference of physiological features of extinct vertebrates. Among them, endothermy is particularly relevant because this feature is linked to a wide array of anatomical, physiological and behavioural features. Endothermy has been defined as the presence of any mechanism of non-shivering thermogenesis that increases both body temperature and resting metabolic rate (RMR) [1]. Mammals, the only extant synapsids, are endotherms [2–5]. The origin of mammalian endothermy is poorly constrained both phylogenetically and temporally, in spite of the fact that the acquisition of this ability is a key innovation (endotherms are less dependent on climatic conditions and can occupy more ecological niches [6]). Many approaches have been used to constrain the phylogenetic and temporal frames of this acquisition. One of them involves identifying unequivocal anatomical correlates of endothermy such as respiratory turbinates or evidence for an insulative pelage [7]. Respiratory turbinates are rarely preserved in fossils but bone ridges of turbinate attachment are first recognizable in therocephalians and in cynodonts [7], so they may have been acquired by the eutheriodonts. Oldest evidence for an insulative pelage (fossilized fur impressions) has been found in the Middle Jurassic non-mammalian therapsids (Castorocauda lutrasimilis [8], Megaconus mammaliaformis [9], Agilodocodon scansorius [10]). Thermal modelling [11], the isotopic composition of mineralized remains [12] and bone palaeohistology [1,13–15] have also been used to infer the thermophysiology of non-mammalian synapsids. Here, we will use this last approach.
Traditionally, qualitative bone histology has been used to estimate the bone growth rate (BGR) [16–18], indirectly linked to the metabolic rate, and to the thermometabolism [19,20]. This framework is based on (A) theoretical grounds ‘the types of tissue deposited in the bones of extinct animals are the most direct evidence of basal metabolic rates, because they directly reflect growth rates […]. The sustained deposition of fast-growing bone tissues, as displayed by mammals, birds and other dinosaurs, must reflect sustained high basal metabolic rates [21, p. 123] and (B) empirical evidence: the variation of BGR significantly explained the variation of RMR in a sample of extant amniotes [19]. More recently, quantitative histology and phylogenetic eigenvector maps (PEMs) [13,22] allowed direct inference of the RMRs of extinct Archosauromorpha [1,13], Sauropterygia [15] and extinct Therapsida [14].
Olivier et al. [14] used this last approach and provided evidence for an ancestral acquisition of endothermy at the node Neotherapsida. However, the sample composition of this study [14] did not allow testing of the hypothesis of an acquisition of endothermy in a more inclusive node. Thus, the present study is aimed at further constraining the temporal range and the phylogenetic frame of the acquisition of endothermy in synapsids. To do so, we will infer the metabolic rates of a sample of extinct synapsids (including Carboniferous non-neotherapsid synapsids) using a recently defined bone histological variable, the relative primary osteon area (RPOA) (named previously ‘primary osteon density’ in [15]), and PEMs [13,22].
2. Material and methods
(a). Material
We analysed femora of a total of 25 species of tetrapods. Seventeen of them are extant tetrapods: three archosaurs (Gallus gallus (Linnaeus, 1758), Anas platyrhynchos (Linnaeus, 1758) and Crocodylus niloticus (Laurenti, 1768)), four lepidosaurs (Varanus exanthematicus (Bosc, 1792), Varanus niloticus (Linnaeus, 1758), Podarcis muralis (Laurenti, 1768) and Zootoca vivipara (Lichtenstein, 1823)), three turtles (Chelodina oblonga (Gray J. E., 1841), Pelodiscus sinensis (Wiegmann, 1835) and Trachemys scripta (Thunberg in Schoepff, 1792)), six mammals (Capreolus capreolus (Linnaeus, 1758), Microcebus murinus (Miller, 1777), Mus musculus (Linnaeus, 1758), Cavia porcellus (Linnaeus, 1758), Lepus europaeus (Pallas, 1778) and Oryctolagus cuniculus (Linaeus, 1758)) and one amphibian (Pleurodeles waltl (Michahelles, 1830)), acting as an outgroup for our analyses.
The remaining eight species are extinct synapsids. The histological thin sections of the Anomodontia (Lystrosaurus sp. (Cope, 1870) and Oudenodon bainii (Owen, 1860)) analysed were previously studied by Olivier et al. [14]. They are the closest relatives of extant mammals in our sample. Both of them come from late Permian and, in the case of Lystrosaurus, it can be found until the early Triassic. The other extinct taxa of the sample are older: Clepsydrops collettii (Cope, 1875), the oldest known synapsid, and Ophiacodon uniformis (Cope, 1878) belong to the Ophiacodontidae clade; Dimetrodon sp. (Cope, 1878) and Sphenacodon sp. (Marsh, 1878) belong to the Sphenacodontidae clade; Mycterosaurus sp. (Williston, 1915) (Varanopidae) and Edaphosaurus boanerges (Romer & Price, 1940) (Edaphosauridae). The oldest one, Clepsydrops collettii, lived in the late Carboniferous. The others are Permian taxa. Extinct taxa were chosen primarily because of their availability at the vertebrate hard tissues histological collection of the Muséum national d'Histoire naturelle (MNHN, Paris).
(b). Methods
(i). Preparation of sections
Femoral diaphyses were embedded in epoxy resin. Transverse and longitudinal thin sections were obtained and mounted on glass slides [23]. These sections were prepared and deposited at the vertebrate hard tissues histological collection of the Paris MNHN, where they are available upon request to the curator (a list of accession numbers is given in electronic supplementary material, file S1). We studied only the femora because it was the only bone present for all of the extinct taxa analysed. Bone histology was studied through transverse sections, and completed, when necessary, by longitudinal sections [24]. The histological terminology follows [25] with addenda from [26].
(ii). Resting metabolic rates
As endothermy cannot be directly inferred from the analysis of bone sections, we used proxies. Metabolic rate is directly linked to the thermometabolism: an endotherm shows a higher metabolic rate than an ectotherm ceteris paribus [3]. Considering that metabolic rate is linked to bone growth rate (BGR) and BGR to histological features, then histological features can be used as a proxy to infer metabolic rates [19,20]. However, considering that metabolic rate is linked to other functions, such as locomotion, digestion, reproduction and regulation, we need to standardize it. For adult endothermic amniotes, the basal metabolic rates has been defined as the minimum rate of energy expenditure measured under thermoneutral and postabsorptive conditions in the inactive phase of the daily cycle [27]. For adult ectothermic amniotes, the standard metabolic rate (SMR) has been defined as the minimum rate of energy expenditure measured at a given temperature within the animal's range of activity [28] or as the metabolic rate ‘measured for fasting individuals during the period of normal inactivity (night for most squamates)’ [29, p. 215]. We used the RMR for the whole sample, defined as the metabolic rate ‘measured for fasting individuals during the period of normal activity’ [29, p. 215].
RMR, measured in ml O2 h−1, is an indicator of the ‘whole’ energetic expenditures of the organism. We need to standardize by mass unit. Thus, we used mass-specific RMR, measured in ml O2 h−1 g−1. The effect of body mass on RMR has been corrected in two different ways in previous studies: (1) the mass-independent RMR measured in millilitres of O2 h−1 g−b, where b is the allometric exponent of the regression between raw RMR and body mass, and (2) the geometry-corrected RMR, measured in ml O2 h−1 g−0.67, where 0.67 is the allometric exponent of the equation surface to body mass for geometrically similar organisms [30]. We used the geometry-corrected RMR because our sample of extant tetrapods includes growing animals and as a consequence the allometric exponent of the regression between raw RMR and body mass may be a mixture of ontogenetic and interspecific allometry (please see [19] for a detailed discussion on this topic). Thus, we used geometry-corrected RMR (ml O2 h−1 g−0.67) measured at the ontogenetic stage of sustained high BGR to standardize data and allow repeatability. All RMR values for extant taxa were taken from the literature: most (14) of them come from Montes et al. [19]. For the remaining three taxa, values were computed using data taken from other studies: Capreolus capreolus from Mauget et al. [31], Lepus europaeus from Hackländer et al. [32], and Oryctolagus cuniculus from Seltmann et al. [33].
(iii). Quantitative histology
We used a variable strongly correlated with the type of osteogenesis (static versus dynamic) involved in bone formation, RPOA, defined as the ratio between the surface occupied by osteon (Sosteon) and the analysed bone surface (Stotal)
This variable was proposed previously and named primary osteon density or POD [15]. We decided to rename it to avoid confusion with the ‘primary osteon diameter’ defined in [34]. Osteon diameter has been shown to be strongly associated with BGR [34]. Considering that BGR significantly explains the variation in RMR [19], both osteon diameter and osteon density are expected to be associated with RMR. Moreover, high growth rate is very energy consuming [19], so a high value of RPOA is expected to reflect a high RMR. Anyway, in spite of these empirical arguments, we tested the relationship between RPOA and RMR using phylogenetic comparative methods.
(c). Phylogenetic comparative methods
(i). Phylogeny
We used phylogenetic comparative methods to infer extinct taxa's RMRs. These methods include statistical analyses that take into consideration phylogenetic relationships as an explanatory factor [35]. Phylogeny includes topology and branch lengths. In this study, branch lengths are computed as the difference in age between two linked nodes (a more inclusive node and a less inclusive node) or between a node and a terminal taxon. Ages of nodes were taken from the PaleoBiology Data Base (https://paleobiodb.org, last accessed 25 June 2018) and reflect the minimal age of the oldest known fossil included in the clade. A minimal distance of 4 Myr was enforced in cases of nodes having the same age, or a distance of less than 4 Myr.
The phylogeny was taken from previous studies [13,14,36] for extant taxa and the two Anomodontia. The relationships of other extinct taxa were taken from Brocklehurst et al. [37], except for Clepsydrops collettii, which was placed according to Laurin & de Buffrénil [38]. We consider the Archelosauria hypothesis of a close relationship between Testudines and Archosauria, supported by many palaeontological [39,40] and molecular [41] studies.
(ii). Phylogenetic generalized least squares
The first step was to test the appropriateness of RPOA as proxy to infer RMR. For this, we quantified the fraction of the variation of RMR explained by the variation of RPOA using phylogenetic generalized least squares (PGLS) regressions [42–44] with the ‘caper’ package [45] in R [46]. If a significant fraction of RMR was explained by the variation of RPOA, then this last variable can be confidently used as a predictor to infer the former in a phylogenetic context. Shapiro–Wilk normality tests were performed on residuals obtained from the PGLS regression of RMR on RPOA using the ‘shapiro.test’ function from the R core software [46].
(iii). Phylogenetic signal
We performed two phylogenetic signal tests (Pagel's λ [47] and Blomberg's κ [48]) using the ‘phytools’ package [49] in R [46].
(iv). Phylogenetic eigenvector maps
The following step was to infer extinct taxa's RMRs, using PEMs [22]. This method infers quantitative values of a biological variable for target taxa using a model. The topology of the phylogeny is coded as a matrix that is afterwards transformed assuming an evolutionary model and taking into account the quantified values in extant taxa, with the aim of representing trait change patterns. Two parameters control the extent of the evolutionary change along the branches. The a steepness parameter (0 ≤ a ≤ 1) indicates how abrupt are evolutionary changes along branches after each split, whereas the ϕ parameter (0 < ϕ < ∞) indicates the relative evolutionary rate [22,50]. We assumed that the trait evolved in a steady manner throughout the phylogeny and consistently we assigned a single pair of values (a and ϕ), but it is possible to assign specific pairs of parameters to each node in a given phylogeny [22]. Under pure Brownian motion (purely neutral evolution), a = 0 and the expected changes are proportional to the square root of the branch lengths [22,50]. By contrast, when a = 1, evolutionary change occurs at a fixed rate irrespective of branch length [22,50]. The a steepness parameter was estimated using the ‘PEM.fitSimple’ function in ‘MPSEM’ [22] and had a value of 0.353 in the model used to perform inferences. We assigned a default value equal to 1 to the ϕ evolutionary rate parameter following Molina-Venegas et al. [50]. Considering that a large number of eigenvectors are produced (n − 1, n being the number of taxa analysed), we used the ‘lmforwardsequentialAICc’ function in MPSEM [22] to perform a forward stepwise selection procedure and compile a set of PEM eigenvectors. Two models are produced, the first one based on the phylogeny only and the second one based on the phylogeny plus a predictor variable (here RPOA). We applied an Akaike information criterion (AIC) [51] to find the best model, i.e. the one with the highest R2 and the lowest AIC value. The chosen model was used to infer a target species' RMR using the ‘MPSEM’ package [22] in R [46]. Finally, we performed a verification of its accuracy using a leave-one-out cross-validation test, by re-estimating RMR values of the extant taxa (for which these values are known) using the inference procedure and comparing the empirical values with the inferred ones using the ‘MPSEM’ package [22] in R [46].
Molina-Venegas et al. [50] analysed accuracy of inferences (here retrodictions) using pGLM and PEM approaches. They concluded that accuracy of predictions is high for traits with high phylogenetic signal (with high Pagel's λ values), and that it decreases when tip branch lengths increase, accuracy being reasonably good for tip branch lengths smaller than 10% of the total length of the tree. In our case study, Pagel's λ for both the response and the explanatory variables are extremely high (see results) and all tip branch lengths but one (Mycterosaurus, see below) are smaller than 10% of the total length of the tree. Therefore, we assume that all our RMR inferences obtained using PEMs are accurate.
(d). Ancestral states reconstruction
Two ancestral states reconstructions were performed. First, we inferred the maximum-likelihood (ML) ancestral states of RMR for all nodes, and the corresponding 95% confidence intervals, using the ‘fastAnc’ function of the phytools package [49] in R [46]. Second, we transformed our results of RMR into a dichotomic character: 0 for ectotherms and 1 for endotherms. The threshold to perform this attribution corresponds to a value (1.5 ml O2 h−1 g−0.67) slightly lower than the lowest RMR values observed in our sample of extant endotherms. These are, for Mus musculus, 1.697, and for Microcebus murinus, 1.526 ml O2 h−1 g−0.67. Thus, a taxon with an inferred value significantly lower than the threshold is scored as ectotherm whereas a taxon with an inferred value significantly higher than the threshold is scored as endotherm. This last optimization was performed using Mesquite software [52], with the ‘Trace Character History’ algorithm, using parsimony.
3. Results
(a). Quantitative histology
Results from histological quantifications are summarized in electronic supplementary material, file S2.
(b). Phylogenetic generalized least squares
We used PGLS analyses to test whether the explanatory (predictor) variable, here RPOA, explains a significant fraction of the response variable (here RMR). We performed a Shapiro–Wilk normality test on residuals obtained from the PGLS regression of RMR on RPOA and we found that the null hypothesis of normality was rejected (p = 0.001939). Thus, we performed a natural logarithm transformation of RMR and a natural logarithm transformation of RPOA + 1 (because several RPOA values equal zero and the natural logarithm of zero is not defined). We repeated the PGLS regression using the transformed variables and the Shapiro–Wilk test on the residuals did not reject the null hypothesis of normality of residuals (p = 0.3014). The p-value of the PGLS regression between ln (RMR) and ln (RPOA + 1) is highly significant (2.092 × 10−6). RPOA explains 79% of the variation of RMR (R² = 0.787, n = 17). The highly significant p-value and high R² found here allow us to use RPOA as a predictor variable to infer RMR using PEMs.
(c). Phylogenetic eigenvector maps
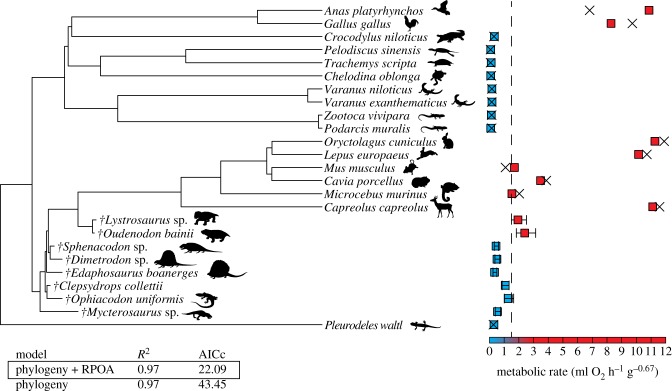
The first step in performing palaeobiological inferences was to choose of the best model. Two models were tested through an AIC procedure: the first one takes into account the phylogenetic relationships, and a second one adds to it the explanatory (predictor) variable (RPOA). A third possibility (a model including only RPOA as an explanatory variable; in other words, a model without phylogeny or including a star phylogeny) has been ruled out because both the response variable (RMR) and the explanatory variable (RPOA) show a highly significant phylogenetic signal. Pagel's λ of ln (RMR) = 0.995, p = 6.577729 × 10−5; Blomberg's κ of ln (RMR) = 1.396; p = 0.001. Pagel's λ of ln (RPOA + 1) = 0.999; p = 0.012; Blomberg's κ of ln (RPOA + 1) = 0.613; p = 0.001. Results of the AIC selection procedure are given in figure 1. The model including RPOA + phylogeny was selected to infer RMR because it shows the highest R squared and the lowest AIC value. Inferred values are shown in figures 1 and 2. Script is provided in electronic supplementary material, file S3. Of our sample of fossil taxa, the value inferred for Oudenodon (2.397 ml O2 h−1 g−0.67) is significantly higher than the threshold separating endotherms from ectotherms (1.500 ml O2 h−1 g−0.67). We inferred a high RMR for Lystrosaurus (1.936 ml O2 h−1 g−0.67), but the inferior limit of the confidence interval is slightly smaller (1.491) than the threshold (1.5). Therefore, we considered that the endothermy of Lystrosaurus was marginally significant. All other extinct taxa show unambiguous ectotherm-like RMR values.
Figure 1.
Resting metabolic rates inferred using palaeohistology and phylogenyetic eigenvector maps. We used a model that includes the phylogeny plus relative primary osteon area as explanatory factors. Shapes of animals are from the PhyloPic database (www.phylopic.org). Blue squares indicate ectothermy and red squares endothermy. The broken line represents the lowest RMR value found in extant endotherms. For extinct taxa, segments represent the 95% confidence intervals of the inferences. For extant taxa, crosses represent values inferred in leave-one-out cross-validation tests. AICc, corrected Akaike information criterion. (Online version in colour.)
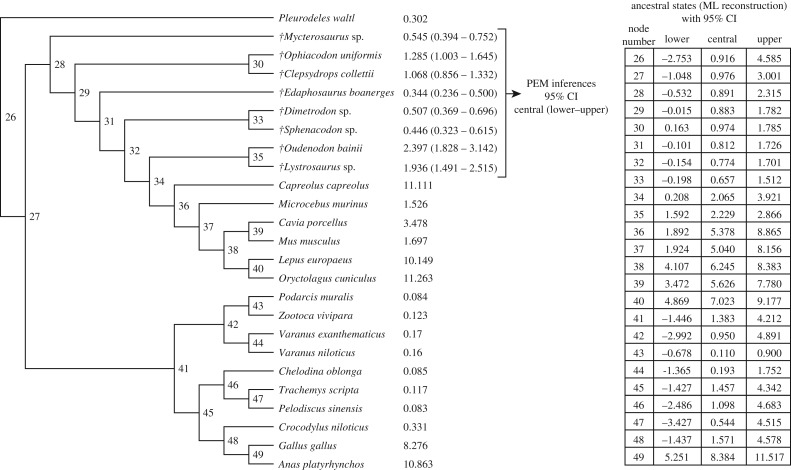
Figure 2.
Maximum-likelihood (ML) ancestral states reconstruction of resting metabolic rates performed using the values inferred using phylogenetic eigenvector maps (PEMs) for the eight extinct synapsids, and the values measured using respirometry in the 17 extant tetrapods. Values are in ml O2 h−1 g−0.67. Within Synapsida, the nodes Anomodontia (node 35) and Mammalia (node 36) were primitively endotherms.
(d). Ancestral states reconstruction
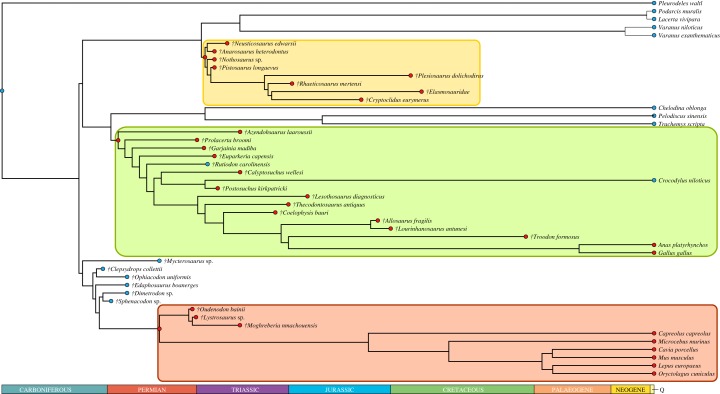
Maximum-likelihood ancestral states reconstructions of RMR using values inferred in this study are shown in figure 2, and a parsimony optimization of the presence of endothermy using the results obtained in the present study and those obtained in previous studies using PEM methodology [1,13–15] is shown in figure 3. We excluded published inferences for two taxa in the optimization of figure 3 because Legendre et al. [13] and Cubo & Jalil [1] found divergent inferred values. These taxa were the archosauriform Proterosuchus fergusi (Broom, 1903) and the dinosaur Maiasaura peeblesorum (Horner & Makela, 1979).
Figure 3.
Parsimony optimization of the presence of endothermy using the results obtained in the present study and those obtained in previous studies using phylogenetic eigenvector maps [1,13–15]. For this, we assigned to each extinct taxon a thermometabolic regime (ectothermy or endothermy) depending on whether the inferred values were significantly higher, lower or not significantly different from the RMR value separating ectotherms from endotherms (1.5 ml O2 h−1 g−0.67). According to this optimization, endothermy arose independently in Archosauromorpha (green), in Sauropterygia (yellow) and in Neotherapsida (orange). Blue circles indicate ectothermy and red circles endothermy. (Online version in colour.)
4. Discussion
The presence of endothermy in extinct synapsids has been inferred using different proxies. Using proxies is obviously necessary because the thermometabolic regime of extinct taxa is not accessible through direct observation of fossilized features. The presence of anatomical features linked to endothermy in extant mammals, such as the presence of fur [53] or of respiratory turbinates [7], has been widely used. The former has traditionally been seen as evidence for, at least, a near-endothermic condition, because of its homeothermic function by retaining the generated heat [7,53]. The earliest known occurrences of fossilized fur impressions have been dated to the Middle Jurassic (Castorocauda [8], Megaconus [9], Agilodocodon [10]). Considering that endothermy has been defined by Cubo & Jalil [1] as the presence of any mechanism of non-shivering thermogenesis (e.g. [5]) that increases both body temperature and RMR, the presence of fur is not definitive evidence for endothermy because, at best, it can indicate a homeothermic condition.
The same reasoning can be applied to respiratory turbinates: these are osseous or cartilaginous convoluted pieces in the nasal cavity. The oldest presence of respiratory turbinates in synapsids dates from the Lopingian (Permian) [54]. Respiratory turbinates warm and moisten the incoming air during inhalation and do the opposite during expiration [54,55]. Doing so, they help to keep a stable temperature and limit the loss of moisture through breathing. According to Ruben, endothermy cannot be sustained without these structures [56], leading them to be considered the best evidence for an endothermic condition. However, the obligate presence of respiratory turbinates to achieve homeothermy has been challenged recently [57].
Another proxy is geochemistry. The isotopic ratio between 16O, the common form of oxygen, and 18O, is used to infer body temperature. This ratio, measured in calcium phosphate from bones and, especially, dentary enamel, is dependent on environmental and body temperatures during the formation of the sample [12,58]. We can infer the relative internal body temperatures from calcium phosphate using fractionation equations [12,58–61]. Lots of studies have been conducted in different organisms, such as ichthyosaurs and plesiosaurs [61]. Recently, Rey et al. [12] studied a large sample of Neotherapsida using this approach and discussed two competing hypotheses: either a single acquisition of endothermy at the Neotherapsida node, or two independent acquisitions at the node Eucynodontia and the node Lystrosauridae + Kannemeyeriiformes. According to these results, the endothermy was acquired in the synapsid clade, during the Guadalupian (Permian) with the single acquisition scenario. With the evolutionary scenario suggesting convergent origin, endothermy may have appeared during the Lopingian (Permian), as for respiratory turbinates.
On the specific case of Dimetrodon, some studies tried to estimate the effect of the sail in thermal regulation [11,62]. Authors created models in order to simulate the heat exchanges and the specific role of the sail. They concluded that the sail allowed Dimetrodon to be active earlier than similar but sail-less predators. However, this proxy deals with external heat income and not with endogenous mechanisms of non-shivering thermogenesis (endothermy).
Bone histology, the last proxy, has largely been based on Amprino's rule [63]: the organization of the collagen matrix records bone growth rate [63]. In other words, fast growth leads to a poorly organized type of tissue (i.e. woven bone), whereas a low growth rate produces a highly organized type of tissue (lamellar or non-lamellar parallel-fibred bone) [25]. Thus the presence of woven bone has been interpreted as evidence for fast bone growth rate, linked to endothermy [64–66]. However, many counterexamples exist: many ectotherms, e.g. Alligator [67] or Varanus [68], are able to form woven bone. By contrast, RPOA, the histological feature recently proposed by Fleischle et al. [15] under the designation ‘primary osteon density’, is tightly linked to bone growth rate and to RMR. Most endothermic amniotes are able to form an initial scaffold composed of woven bone that includes large cavities and produces a rapid volume expansion of the cortex during early ontogenetic stages (e.g. in the long bones of ratites [69] and in the long bones of the king penguin [70]). On the contrary, in most ectothermic amniotes, periosteal bone is composed of parallel-fibred bone including small cavities, if any, and producing a slow volume expansion of the cortex (e.g. in squamates [71]). Consistently, RPOA was used in this study to infer the thermometabolic regime (ectothermic or endothermic) of our sample of extinct synapsids.
RPOA explains a significant fraction of the variation of RMR (quantified using respirometry) in the sample of extant tetrapods (results obtained using PGLS regressions). Thus, assuming the actualism principle, a priori the former can be used to infer the latter in extinct taxa. Inferred RMR values for our sample of extinct synapsids using PEMs are shown in figures 1 and 2. The value inferred for Mycterosaurus should be analysed with caution because the branch length of this taxon (42.3 Myr) is bigger than 10% of the total height of the tree (358.9 Myr) and, according to [50], this fact leads to a loss of accuracy when performing inferences. Our inferences for Lystrosaurus sp. (1.936 ml O2 h−1 g−0.67; 1.491–2.515) and Oudenodon bainii (2.397 ml O2 h−1 g−0.67; 1.828–3.142) are congruent with those obtained by Olivier et al. [14], who used a different histological feature (osteocyte lacunae density). We performed maximum-likelihood ancestral states reconstructions using these values and those measured in extant species (figure 2). As expected, RMRs inferred for nodes 49 (birds) and 36 (mammals) in figure 2 are significantly higher than the threshold separating endotherms from ectotherms (1.5 ml O2 h−1 g−0.67). Likewise, RMR inferred for node 35 (Anomodontia: (Lystrosaurus-Oudenodon)) is also significantly higher than the quoted threshold. However, the value inferred for node 34 (Therapsida): (Lystrosaurus-Oudenodon) Mammals) does not exclude ectothermy. Finally, we performed a parsimony optimization of the presence of endothermy (figure 3). For this, we assigned to each extinct taxon a thermometabolic regime (ectothermy or endothermy) depending on whether the inferred values were significantly higher, lower or not significantly different from the RMR value separating ectotherms from endotherms (1.5 ml O2 h−1 g−0.67), using the results obtained in the present study and those obtained in previous studies using PEMs [1,13–15]. According to the reconstructed ancestral thermometabolic regime, endothermy arose three independent times in amniotes: in Archosauromorpha, in Sauropterygia and in Neotherapsida (figure 3).
The thermometabolism of other groups of tetrapods has been analysed: ichthyosaurs, mosasaurs, pterosaurs and Thalattoshuchia. A study using geochemistry suggested a high inner temperature and a fully developed endothermic condition for ichthyosaurs and a medium inner temperature and an incipient endothermy for mosasaurs [61]. This result is congruent with that obtained by de Buffrénil & Mazin, who found the presence of woven bone, suggesting a high growth rate and, so, a high metabolic rate in ichthyosaurs [72]. The case of mosasaurs is more complex. Houssaye et al. [73] analysed the bone histology of mosasaur limb bones and found a predominance of parallel-fibred bone, which doesnot need a high metabolic rate to occur. But they also described unusual parallel-fibred bone, which could reflect a growth rate intermediate between that typical of parallel-fibred bones and that associated with woven bone. The thermometabolic condition of mosasaurs is ambiguous, and gigantothermy, a heat conservation mechanism, linked to high body mass, is not excluded [73]. For pterosaurs, de Ricqlès et al. [74]) analysed the histology of limb bones and found the presence of woven bone, especially in juvenile specimens, leading them to the conclusion that these animals had a growth curve similar to those found in extant birds. A high growth rate suggests an endothermic condition for pterosaurs. This condition would be correlated with the presence of air sacs detected in some species [75]. Such organs are very important in modern birds to sustain a unidirectional airflow in the lungs and a high metabolic rate associated with flight. The finding of unidirectional airflow in the lungs of alligators [76] suggests that this condition would be primitive for archosaurs. Finally, Séon et al. [77] have shown that Thalattosuchia (marine crocodylomorphs) had body temperatures intermediate between those of typical ectotherms and those of typical endotherms. Among them, metriorhynchids (pelagic active predators) may have been slightly warmer than teleosaurids (coastal ambush predators) [77].
Supplementary Material
Supplementary Material
Supplementary Material
Acknowledgements
We thank H. Lamrous and S. Morel for preparation of thin sections, D. Germain for access to the hard tissue collection of the French Muséum national d'Histoire naturelle, C. Olivier for reading a draft of the paper, and L. Legendre for useful discussions about phylogenetic eigenvector maps.
Perspectives
Further research using quantitative histology and PEMs will help to elucidate the thermometabolic condition of ichthyosaurs, pterosaurs, mosasaurs, Thalattosuchia and early synapsids. The predictive power of inference models will increase by including additional explanatory factors such as life-history traits, as well as new osteohistological features correlated to thermometabolism, such as for instance, minimum diameter of vascular canals [78].
Data accessibility
The electronic supplementary material contains new data used in the analyses performed in this study
Authors' contributions
J.C. designed research; M.G.F.-B. performed histological quantifications, adapted the script from sources and made statistical analyses; J.C. and M.G.F.-B. wrote the paper
Competing interests
We declare we have no competing interests
References
- 1.Cubo J, Jalil N-E. 2019. Bone histology of Azendohsaurus laaroussii: implications for the evolution of thermometabolism in Archosauromorpha. Paleobiology 45, 317–330. ( 10.1017/pab.2019.13) [DOI] [Google Scholar]
- 2.Hillenius WJ, Ruben JA. 2004. The evolution of endothermy in terrestrial vertebrates: who? when? why? Physiol. Biochem. Zool. 77, 1019–1042. ( 10.1086/425185) [DOI] [PubMed] [Google Scholar]
- 3.Clarke A, Pörtner H-O. 2010. Temperature, metabolic power and the evolution of endothermy. Biol. Rev. 85, 703–727. ( 10.1111/j.1469-185X.2010.00122.x) [DOI] [PubMed] [Google Scholar]
- 4.Nespolo RF, Bacigalupe LD, Figueroa CC, Koteja P, Opazo JC. 2011. Using new tools to solve an old problem: the evolution of endothermy in vertebrates. Trends Ecol. Evol. 26, 414–423. ( 10.1016/j.tree.2011.04.004) [DOI] [PubMed] [Google Scholar]
- 5.Rowland LA, Bal NC, Periasamy M. 2015. The role of skeletal-muscle-based thermogenic mechanisms in vertebrate endothermy: non-shivering thermogenic mechanisms in evolution. Biol. Rev. 90, 1279–1297. ( 10.1111/brv.12157) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Walter I, Seebacher F. 2009. Endothermy in birds: underlying molecular mechanisms. J. Exp. Biol. 212, 2328–2336. ( 10.1242/jeb.029009) [DOI] [PubMed] [Google Scholar]
- 7.Ruben JA, Hillenius WJ, Kemp TS, Quick DE. 2012. The evolution of mammalian endothermy. In Forerunners of mammals: radiation, histology, biology (ed. Chinsamy-Turan A), pp. 273–286. Bloomington, IN: Indiana University Press. [Google Scholar]
- 8.Ji Q, Luo Z-X, Yuan C-X, Tabrum AR. 2006. A swimming mammaliaform from the Middle Jurassic and ecomorphological diversification of early mammals. Science 311, 1123–1127. ( 10.1126/science.1123026) [DOI] [PubMed] [Google Scholar]
- 9.Zhou C-F, Wu S, Martin T, Luo Z-X. 2013. A Jurassic mammaliaform and the earliest mammalian evolutionary adaptations. Nature 500, 163–167. ( 10.1038/nature12429) [DOI] [PubMed] [Google Scholar]
- 10.Meng Q-J, Ji Q, Zhang Y-G, Liu D, Grossnickle DM, Luo Z-X. 2015. An arboreal docodont from the Jurassic and mammaliaform ecological diversification. Science 347, 764–768. ( 10.1126/science.1260879) [DOI] [PubMed] [Google Scholar]
- 11.Florides GA, Kalogirou SA, Tassou SA, Wrobel L. 2001. Natural environment and thermal behaviour of Dimetrodon limbatus. J. Therm. Biol. 26, 15–20. ( 10.1016/S0306-4565(00)00019-X) [DOI] [PubMed] [Google Scholar]
- 12.Rey K, et al. 2017. Oxygen isotopes suggest elevated thermometabolism within multiple Permo-Triassic therapsid clades. eLife 6, e28589 ( 10.7554/eLife.28589) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Legendre LJ, Guénard G, Botha-Brink J, Cubo J. 2016. Palaeohistological evidence for ancestral high metabolic rate in archosaurs. Syst. Biol. 65, 989–996. ( 10.1093/sysbio/syw033) [DOI] [PubMed] [Google Scholar]
- 14.Olivier C, Houssaye A, Jalil N-E, Cubo J. 2017. First palaeohistological inference of resting metabolic rate in an extinct synapsid, Moghreberia nmachouensis (Therapsida: Anomodontia). Biol. J. Linn. Soc. 121, 409–419. ( 10.1093/biolinnean/blw044) [DOI] [Google Scholar]
- 15.Fleischle CV, Wintrich T, Sander PM. 2018. Quantitative histological models suggest endothermy in plesiosaurs. PeerJ 6, e4955 ( 10.7717/peerj.4955) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Padian K, de Ricqlès AJ, Horner JR. 2001. Dinosaurian growth rates and bird origins. Nature 412, 405–408. ( 10.1038/35086500) [DOI] [PubMed] [Google Scholar]
- 17.Padian K, Horner JR, De Ricqlès A. 2004. Growth in small dinosaurs and pterosaurs: the evolution of archosaurian growth strategies. J. Vertebr. Paleontol. 24, 555–571. ( 10.1671/0272-4634(2004)024[0555:GISDAP]2.0.CO;2) [DOI] [Google Scholar]
- 18.Botha-Brink J, Smith RMH. 2011. Osteohistology of the Triassic archosauromorphs Prolacerta, Proterosuchus, Euparkeria, and Erythrosuchus from the Karoo Basin of South Africa. J. Vertebr. Paleontol. 31, 1238–1254. ( 10.1080/02724634.2011.621797) [DOI] [Google Scholar]
- 19.Montes L, Le Roy N, Perret M, de Buffrénil V, Castanet J, Cubo J. 2007. Relationships between bone growth rate, body mass and resting metabolic rate in growing amniotes: a phylogenetic approach. Biol. J. Linn. Soc. 92, 63–76. ( 10.1111/j.1095-8312.2007.00881.x) [DOI] [Google Scholar]
- 20.Montes L, Castanet J, Cubo J. 2010. Relationship between bone growth rate and bone tissue organization in amniotes: first test of Amprino's rule in a phylogenetic context. Anim. Biol. 60, 25–41. ( 10.1163/157075610X12610595764093) [DOI] [Google Scholar]
- 21.Padian K, Horner JR. 2002. Typology versus transformation in the origin of birds. Trends Ecol. Evol. 17, 120–124. ( 10.1016/S0169-5347(01)02409-0) [DOI] [Google Scholar]
- 22.Guénard G, Legendre P, Peres-Neto P. 2013. Phylogenetic eigenvector maps: a framework to model and predict species traits. Methods Ecol. Evol. 4, 1120–1131. ( 10.1111/2041-210X.12111) [DOI] [Google Scholar]
- 23.Lamm E-T. 2013. Preparation and sectioning of specimens. In Bone histology of fossil tetrapods: advancing methods, analysis, and interpretation (eds Padian K, Lamm E-T), pp. 55–160. Berkeley, CA: University of California Press. [Google Scholar]
- 24.Faure-Brac MG, Pelissier F, Cubo J. 2019. The influence of plane of section on the identification of bone tissue types in amniotes with implications for paleophysiological inferences. J. Morphol. 280, 1282–1291. ( 10.1002/jmor.21030) [DOI] [PubMed] [Google Scholar]
- 25.Francillon-Vieillot H, de Buffrénil V, Castanet J, Géraudie J, Meunier FJ, Sire J-Y, Zylberberg L, De Ricqlès A. 1990. Microstructure and mineralization of vertebrate skeletal tissues. In Skeletal biomineralization: patterns, processes and evolutionary trends (ed. Careter JG.), pp. 471–530. New York, NY: Van Nostrand Reinhold. [Google Scholar]
- 26.Prondvai E, Stein KHW, de Ricqlès A, Cubo J. 2014. Development-based revision of bone tissue classification: the importance of semantics for science: development-based bone tissue classification. Biol. J. Linn. Soc. 112, 799–816. ( 10.1111/bij.12323) [DOI] [Google Scholar]
- 27.Daan S, Masman D, Groenewold A. 1990. Avian basal metabolic rates: their association with body composition and energy expenditure in nature. Am. J. Physiol. Regul. Integr. Comp. Physiol. 259, 333–340. ( 10.1152/ajpregu.1990.259.2.R333) [DOI] [PubMed] [Google Scholar]
- 28.Lewis LY, Gatten RE Jr. 1985. Aerobic metabolism of American alligators, Alligator mississippiensis, under standard conditions and during voluntary activity. Comp. Biochem. Physiol. A 80, 441–447. ( 10.1016/0300-9629(85)90065-9) [DOI] [PubMed] [Google Scholar]
- 29.Andrews RM, Pough FH. 1985. Metabolism of squamate reptiles: allometric and ecological relationships. Physiol. Biochem. Zool. 58, 214–231. ( 10.1086/physzool.58.2.30158569) [DOI] [Google Scholar]
- 30.White CR, Seymour RS. 2005. Sample size and mass range effects on the allometric exponent of basal metabolic rate. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 142, 74–78. ( 10.1016/j.cbpa.2005.07.013) [DOI] [PubMed] [Google Scholar]
- 31.Mauget C, Mauget R, Sempéré A. 1999. Energy expenditure in European roe deer fawns during the suckling period and its relationship with maternal reproductive cost. Can. J. Zool. 77, 389–396. ( 10.1139/z98-230) [DOI] [Google Scholar]
- 32.Hackländer K, Arnold W, Ruf T. 2002. Postnatal development and thermoregulation in the precocial European hare (Lepus europaeus). J. Comp. Physiol. B 172, 183–190. ( 10.1007/s00360-001-0243-y) [DOI] [PubMed] [Google Scholar]
- 33.Seltmann MW, Ruf T, Rödel HG. 2009. Effects of body mass and huddling on resting metabolic rates of post-weaned European rabbits under different simulated weather conditions. Funct. Ecol. 23, 1070–1080. ( 10.1111/j.1365-2435.2009.01581.x) [DOI] [Google Scholar]
- 34.de Margerie E, Cubo J, Castanet J. 2002. Bone typology and growth rate: testing and quantifying ‘Amprino's rule’ in the mallard (Anas platyrhynchos). C. R. Biol. 325, 221–230. ( 10.1016/S1631-0691(02)01429-4) [DOI] [PubMed] [Google Scholar]
- 35.Felsenstein J. 1985. Phylogenies and the comparative method. Am. Nat. 125, 1–15. ( 10.1086/284325) [DOI] [Google Scholar]
- 36.Cubo J, Le Roy N, Martinez-Maza C, Montes L. 2012. Paleohistological estimation of bone growth rate in extinct archosaurs. Paleobiology 38, 335–349. ( 10.1666/08093.1) [DOI] [Google Scholar]
- 37.Brocklehurst N, Reisz RR, Fernandez V, Fröbisch J. 2016. A re-description of ‘Mycterosaurus’ smithae, an Early Permian eothyridid, and its impact on the phylogeny of pelycosaurian-grade synapsids. PLoS ONE 11, e0156810 ( 10.1371/journal.pone.0156810) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Laurin M, de Buffrénil V. 2016. Microstructural features of the femur in early ophiacodontids: a reappraisal of ancestral habitat use and lifestyle of amniotes. C. R. Palevol. 15, 115–127. ( 10.1016/j.crpv.2015.01.001) [DOI] [Google Scholar]
- 39.Bever GS, Lyson TR, Field DJ, Bhullar B-AS. 2015. Evolutionary origin of the turtle skull. Nature 525, 239–242. ( 10.1038/nature14900) [DOI] [PubMed] [Google Scholar]
- 40.Schoch RR, Sues H-D. 2015. A Middle Triassic stem-turtle and the evolution of the turtle body plan. Nature 523, 584–587. ( 10.1038/nature14472) [DOI] [PubMed] [Google Scholar]
- 41.Crawford NG, Parham JF, Sellas AB, Faircloth BC, Glenn TC, Papenfuss TJ, Henderson JB, Hansen MH, Simison WB. 2015. A phylogenomic analysis of turtles. Mol. Phylogenet. Evol. 83, 250–257. ( 10.1016/j.ympev.2014.10.021) [DOI] [PubMed] [Google Scholar]
- 42.Garland T, Ives AR. 2000. Using the past to predict the present: confidence intervals for regression equations in phylogenetic comparative methods. Am. Nat. 155, 346–364. ( 10.1086/303327) [DOI] [PubMed] [Google Scholar]
- 43.Martins EP, Hansen TF. 1997. Phylogenies and the comparative method: a general approach to incorporating phylogenetic information into the analysis of interspecific data. Am. Nat. 149, 646–667. ( 10.1086/286013) [DOI] [Google Scholar]
- 44.Grafen A. 1989. The phylogenetic regression. Phil. Trans. R. Soc. Lond. B 326, 119–157. ( 10.1098/rstb.1989.0106) [DOI] [PubMed] [Google Scholar]
- 45.Orme D. 2013. The caper package: comparative analysis of phylogenetics and evolution in R. See https://cran.r-project.org/web//packages/caper/vignettes/caper.pdf.
- 46.R Development Core Team. 2008. R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; See http://www.R-project.org. [Google Scholar]
- 47.Pagel M. 1999. Inferring the historical patterns of biological evolution. Nature 401, 877–884. ( 10.1038/44766) [DOI] [PubMed] [Google Scholar]
- 48.Blomberg SP, Garland T, Ives AR. 2003. Testing for phylogenetic signal in comparative data: behavioral traits are more labile. Evolution 57, 717–745. ( 10.1111/j.0014-3820.2003.tb00285.x) [DOI] [PubMed] [Google Scholar]
- 49.Revell LJ. 2012. Phytools: an R package for phylogenetic comparative biology (and other things). Methods Ecol. Evol. 3, 217–223. ( 10.1111/j.2041-210X.2011.00169.x) [DOI] [Google Scholar]
- 50.Molina-Venegas R, Moreno-Saiz JC, Castro Parga I, Davies TJ, Peres-Neto PR, Rodríguez MÁ. 2018. Assessing among-lineage variability in phylogenetic imputation of functional trait datasets. Ecography 41, 1740–1749. ( 10.1111/ecog.03480) [DOI] [Google Scholar]
- 51.Akaike H. 1973. Information theory and an extension of the maximum likelihood principle. In Proc. 2nd Int. Symp. Information Theory (eds Petrov BN, Csaki F.), pp. 267–281. Budapest, Hungary: Akademiai Kiado. [Google Scholar]
- 52.Maddison WP, Maddison DR. 2018. Mesquite: a modular system for evolutionary analysis. See http://www.mesquiteproject.org.
- 53.Meng J, Hu Y, Li C, Wang Y. 2006. The mammal fauna in the Early Cretaceous Jehol Biota: implications for diversity and biology of Mesozoic mammals. Geol. J. 41, 439–463. ( 10.1002/gj.1054) [DOI] [Google Scholar]
- 54.Hillenius WJ. 1992. The evolution of nasal turbinates and mammalian endothermy. Paleobiology 18, 17–29. ( 10.1017/S0094837300012197) [DOI] [Google Scholar]
- 55.Geist NR. 2000. Nasal respiratory turbinate function in birds. Physiol. Biochem. Zool. 73, 581–589. ( 10.1086/317750) [DOI] [PubMed] [Google Scholar]
- 56.Ruben JA. 1995. The evolution of endothermy in mammals and birds: from physiology to fossils. Annu. Rev. Physiol. 57, 69–95. ( 10.1146/annurev.ph.57.030195.000441) [DOI] [PubMed] [Google Scholar]
- 57.Crompton AW, Owerkowicz T, Bhullar B-AS, Musinsky C. 2017. Structure of the nasal region of non-mammalian cynodonts and mammaliaforms: speculations on the evolution of mammalian endothermy. J. Vertebr. Paleontol. 37, e1269116 ( 10.1080/02724634.2017.1269116) [DOI] [Google Scholar]
- 58.Lécuyer C, Bogey C, Garcia J-P, Grandjean P, Barrat J-A, Floquet M, Bardet N, Pereda-Superbiola X. 2003. Stable isotope composition and rare earth element content of vertebrate remains from the Late Cretaceous of northern Spain (Laño): did the environmental record survive? Palaeogeogr. Palaeoclimatol. Palaeoecol. 193, 457–471. ( 10.1016/S0031-0182(03)00261-X) [DOI] [Google Scholar]
- 59.Amiot R, Lécuyer C, Buffetaut E, Escarguel G, Fluteau F, Martineau F. 2006. Oxygen isotopes from biogenic apatites suggest widespread endothermy in Cretaceous dinosaurs. Earth Planet. Sci. Lett. 246, 41–54. ( 10.1016/j.epsl.2006.04.018) [DOI] [Google Scholar]
- 60.Amiot R, et al. 2010. Oxygen isotope evidence for semi-aquatic habits among spinosaurid theropods. Geology 38, 139–142. ( 10.1130/G30402.1) [DOI] [Google Scholar]
- 61.Bernard A, et al. 2010. Regulation of body temperature by some Mesozoic marine reptiles. Science 328, 1379–1382. ( 10.1126/science.1187443) [DOI] [PubMed] [Google Scholar]
- 62.Haack SC. 1986. A thermal model of the sailback pelycosaur. Paleobiology 12, 450–458. ( 10.1017/S009483730000316X) [DOI] [Google Scholar]
- 63.Amprino R. 1947. La structure du tissu osseux envisagée comme expression de différences dans la vitesse de l'accroissement. Arch. Biol. Liege 58, 315–330. [In French.] [Google Scholar]
- 64.de Ricqlès A. 1974. Evolution of endothermy: histological evidence. Evol. Theory 1, 51–80. [Google Scholar]
- 65.Chinsamy A, Rubidge BS. 1993. Dicynodont (Therapsida) bone histology: phylogenetic and physiological implications. Palaeontol. Afr. 30, 97–102. [Google Scholar]
- 66.Botha J, Chinsamy A. 2001. Growth patterns deduced from the bone histology of the cynodonts Diademodon and Cygnognathus. J. Vertebr. Paleontol. 20, 705–711. ( 10.1671/0272-4634(2000)020[0705:GPDFTB]2.0.CO;2) [DOI] [Google Scholar]
- 67.Tumarkin-Deratzian AR, Vann DR, Dodson P. 2007. Growth and textural ageing in long bones of the American alligator Alligator mississippiensis (Crocodylia: Alligatoridae). Zool. J. Linn. Soc. 150, 1–39. ( 10.1111/j.1096-3642.2007.00283.x) [DOI] [Google Scholar]
- 68.de Buffrénil V, Castanet J. 2000. Age estimation by skeletochronology in the Nile monitor (Varanus niloticus), a highly exploited species. J. Herpetol. 34, 414 ( 10.2307/1565365) [DOI] [Google Scholar]
- 69.Castanet J, Curry K, Cubo J, Boisard J-J. 2000. Periosteal bone growth rates in extant ratites (ostriche and emu). Implications for assessing. C. R. Acad. Sci. Ser III Sci. Vie 323, 543–550. ( 10.1016/s0764-4469(00)00181-5) [DOI] [PubMed] [Google Scholar]
- 70.De Margerie E, Robin J-P, Verrier D, Cubo J, Groscolas R, Castanet J. 2004. Assessing a relationship between bone microstructure and growth rate: a fluorescent labelling study in the king penguin chick (Aptenodytes patagonicus). J. Exp. Biol. 207, 869–879. ( 10.1242/jeb.00841) [DOI] [PubMed] [Google Scholar]
- 71.Castanet J. 1978. [Skeletal annulations as age indicators in lizards]. Acta Zool. 59, 35–48. [In French with an English abstract.] ( 10.1111/j.1463-6395.1978.tb00109.x) [DOI] [Google Scholar]
- 72.de Buffrénil V, Mazin J-M. 1990. Bone histology of the ichthyosaurs: comparative data and functional interpretation. Paleobiology 16, 435–447. ( 10.1017/S0094837300010174) [DOI] [Google Scholar]
- 73.Houssaye A, Lindgren J, Pellegrini R, Lee AH, Germain D, Polcyn MJ. 2013. Microanatomical and histological features in the long bones of mosasaurine mosasaurs (Reptilia, Squamata) – implications for aquatic adaptation and growth rates. PLoS ONE 8, e76741 ( 10.1371/journal.pone.0076741) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.de Ricqlès AJ, Padian K, Horner JR, Francillon-Vieillot H. 2000. Palaeohistology of the bones of pterosaurs (Reptilia: Archosauria): anatomy, ontogeny, and biomechanical implications. Zool. J. Linn. Soc. 129, 349–385. ( 10.1111/j.1096-3642.2000.tb00016.x) [DOI] [Google Scholar]
- 75.Butler RJ, Barrett PM, Gower DJ. 2009. Postcranial skeletal pneumaticity and air-sacs in the earliest pterosaurs. Biol. Lett. 5, 557–560. ( 10.1098/rsbl.2009.0139) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Farmer CG, Sanders K. 2010. Unidirectional airflow in the lungs of alligators. Science 327, 338–340. ( 10.1126/science.1180219) [DOI] [PubMed] [Google Scholar]
- 77.Séon N, Amiot R, Martin JE, Young MT, Middleton H, Fourel F, Picot L, Valentin X, Lecuyer C. 2020. Thermophysiologies of Jurassic marine crocodylomorphs inferred from the oxygen isotope composition of their tooth apatite. Phil. Trans. R. Soc. B 375, 20190139 ( 10.1098/rstb.2019.0139) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Huttenlocker AK, Farmer CG. 2017. Bone microvasculature tracks red blood cell size diminution in Triassic mammal and dinosaur forerunners. Curr. Biol. 27, 48–54. ( 10.1016/j.cub.2016.10.012) [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The electronic supplementary material contains new data used in the analyses performed in this study