ACCELERATED DYNAMIC MRI USING STRUCTURED LOW RANK MATRIX COMPLETION

Arvind Balachandrasekaran; Greg Ongie; Mathews Jacob

doi:10.1109/icip.2016.7532680

. Author manuscript; available in PMC: 2021 Feb 16.

Published in final edited form as: Proc Int Conf Image Proc. 2016 Aug 19;2016:1858–1862. doi: 10.1109/icip.2016.7532680

ACCELERATED DYNAMIC MRI USING STRUCTURED LOW RANK MATRIX COMPLETION

Arvind Balachandrasekaran ^†, Greg Ongie ^*, Mathews Jacob ^†

PMCID: PMC7885618 NIHMSID: NIHMS1667948 PMID: 33597830

Abstract

We introduce a fast structured low-rank matrix completion algorithm with low memory & computational demand to recover the dynamic MRI data from undersampled measurements. The 3-D dataset is modeled as a piecewise smooth signal, whose discontinuities are localized to the zero sets of a bandlimited function. We show that a structured matrix corresponding to convolution with the Fourier coefficients of the signal derivatives is highly low-rank. This property enables us to recover the signal from undersampled measurements. The application of this scheme in dynamic MRI shows significant improvement over state of the art methods.

Keywords: dynamic MRI, structured low rank, smoothness regularization

1. INTRODUCTION

Obtaining high spatial & temporal resolution is challenging in dynamic MRI, mainly due to the slow nature of acquisition. A common approach to speed up the acquisition is to acquire undersampled Fourier data and to regularize the recovery problem using appropriate priors. Common regularization penalties include ℓ₁ sparsity prior in the Fourier/wavelet domain and smoothness priors (e.g. total variation regularization).

Recently, structured low rank matrix priors are emerging as powerful alternatives for classical ℓ₁ regularization [1-4]. For example, we have modeled a 2-D image as a piecewise smooth signal, whose partial derivatives are localized to zero-crossings of a band limited trigonometric polynomial [3, 4]; this work is inspired by [5]. We have shown that such a signal can be annihilated by a large set of finite impulse response filters in the Fourier domain. These annihilation relations imply that a matrix with convolutional structure derived from the uniform Fourier samples of the signal is low-rank. We have exploited this property to recover the image from uniform [6] and non-uniform samples [7]. Since these methods can exploit the additional structure in many multidimensional problems (e.g. smoothness of the edges), on top of sparsity, they are demonstrated to yield better reconstruction performance than classical total variation methods. These methods are generalization of classical 1-D FRI methods [8, 9] to the multidimensional setting with non-uniform sampling.

Despite improved performance, structured low rank methods suffer from high memory demand and computational complexity, both resulting from the lifting of the original 2-D problem to a dense high-dimensional structured matrix. Since the dimension of the matrix is atleast two to three orders of magnitude greater than the size of the original data, it results in computationally expensive algorithms. Various methods have been explored to make the computational complexity manageable. For example, greedy multi-scale approximations to sequentially recover the image [1] and factorization of the matrix to two low-dimensional matrices have been explored [1, 2]. Despite these approximations, it is still challenging to extend the above scheme to three dimensions and beyond. Current methods recover 2-D slices of the 3D datasets independently [1], which is suboptimal and requires Cartesian undersampling; this approach is not as efficient as more general non-Cartesian acquisition schemes. Another challenge with most of the current methods is that they are only designed for one derivative operator. [1, 2]. When multiple derivative operators are desired (e.g. directional derivatives), the problems are solved in a sequential fashion; the data recovered using one weighting is then used to recover the image with the other weighting.

Recently, we have introduced a fast and memory efficient structured low-rank matrix recovery algorithm called Generic Iteratively Reweighted Annihilating Filter (GIRAF) [10]. This approach works in the unlifted domain & exploits the convolutional structure of the structured matrix using Fast Fourier Transforms (FFT), which quite significantly reduces the computational complexity and memory demand of the algorithm. In addition, the algorithm is also general enough to handle arbitrary number of k-space weightings at the same time. In this paper, we extend the GIRAF algorithm to recover signals that can be modeled as piecewise smooth functions in three dimensions. We demonstrate the improvement offered by this algorithm on breath held cine data over spatio-temporal total variation (TV) & temporal Fourier sparsity regularized reconstruction schemes.

2. THEORY

Consider the general class of piecewise smooth functions g of degree n in d dimensions:

g (r) = \sum_{i = 1}^{N} g_{i} (r) χ_{Ω_{1}} (r), \forall r = (x, y) \in [0, 1]^{d},

(1)

where χ_{Ω_i} is a characteristic function of the region Ω_i and g_i are smooth polynomial functions of degree at most n. We assume that the edge set $\partial Ω = ⋃_{i = 1}^{N} \partial Ω_{i}$ coincides with the zero level sets of a d dimensional bandlimited function:

μ (r) = \sum_{k \in Δ} c [k] e^{j 2 π 〈 k, r 〉}, \forall r = (x, y) \in [0, 1]^{d}

(2)

where $c [k] \in C$ are the Fourier coefficients of μ and Δ is any finite subset of $Z^{2}$ . We have shown that such signals satisfy

(\partial_{x_{1}}^{n_{1}} \dots \partial_{x_{d}}^{n_{d}} g) \cdot ϕ = 0; \forall n_{1} + \dots n_{d} = n + 1,

(3)

where ϕ = μ · η is any function bandlimited to Λ₁ ⊇ Δ, with a factor μ. The above conditions (3) translates into a convolution relation in the Fourier domain.

((j ω_{1})^{n_{1}} \dots (j ω_{d})^{n_{d}} \hat{g}) ⋆ c = 0; \forall n_{1} + \dots + n_{d} = n + 1

(4)

We consider the recovery of the the Fourier coefficients on a rectangular region $Γ \subset Z^{d}$ . When n = 0 in (3), we obtain a piecewise constant signal model with conditions similar to the assumptions in classical total variation regularization. The annihilation relations in this case can be compactly written in matrix form as

T (\hat{g}) h = [\begin{matrix} T_{1} (\hat{g}) \\ ⋮ \\ T_{d} (\hat{g}) \end{matrix}] h = 0

(5)

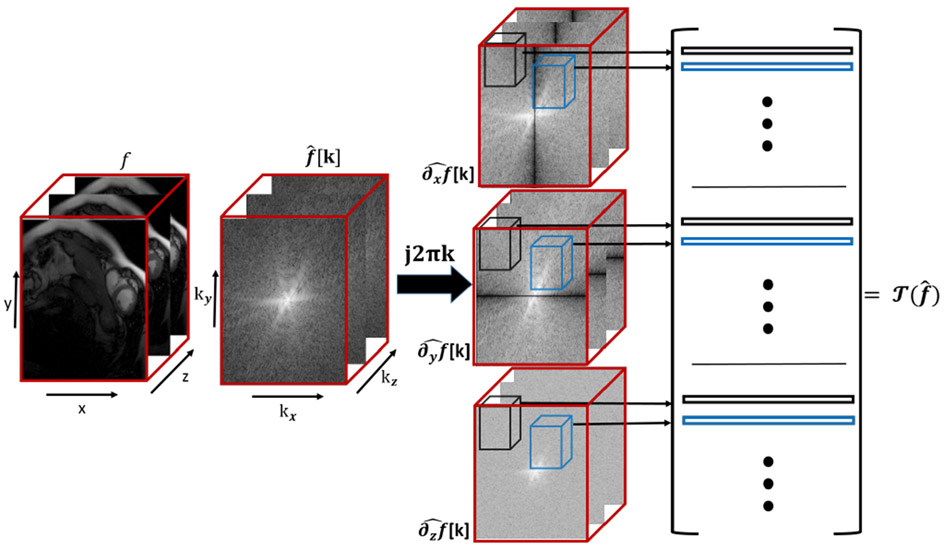
Here, $T_{i} (\hat{g}) \in C^{∣ Λ_{2} ∣ \times ∣ Λ_{1} ∣}$ is a Toeplitz/Hankel matrix whose entries are derived from $j ω_{i} \hat{g}; T_{i} (\hat{g}) h$ corresponds to the convolution of $j ω_{i} \hat{g}$ with h. Here, $h \overset{F}{\leftrightarrow} ϕ$ is a d dimensional filter, supported in Λ₁. We have shown that the dimension of the space of filters h that satisfy (5) is given by the size of the set Λ₁∣Δ — the valid shifts of the set Δ within Λ₁. Λ₂ ∈ Γ indicates the set of indices over which the convolutions between the samples of $\hat{g}$ and h are valid. See Fig. 1 for an illustration of the structure of the lifted matrix $T (\hat{g})$ . Since the annihilation conditions are satisfied for filters h that live in a large subspace, we can conclude that $T (\hat{g})$ is low rank. We use this property to recover $\hat{g}$ from non-uniform samples.

Fig. 1: — Illustration of the lifted matrix $T (G)$ : The rows of the matrix are cube shape neighborhoods of the weighted Fourier samples corresponding to the partial derivatives. We use the structure of the low-rank matrix to recover it from few measurements as in (9).

3. PROPOSED FORMULATION

3.1. Measurement Model

Let $\tilde{G} \in C^{P \times T}$ denote the Casoratti matrix structure of the dynamic MRI dataset, where each column ${\tilde{G}}_{i}$ represents a vectorized image at a time point t_i. We consider the recovery of the 3-D discrete Fourier coefficients of $\tilde{G}$ , denoted by G. The Fourier measurements b can be modeled as:

b = {SF}_{t} G + η;

(6)

where S and η are the sampling matrix and zero mean white Gaussian noise vector respectively. F_t is the 1-D discrete inverse Fourier transform (DFT) matrix along the time direction. (6) can be compactly written as

b = A (G) + η

(7)

where $A$ is the measurement operator.

3.2. Problem formulation

We assume that the time series of MR images can be modeled as three dimensional piecewise constant functions and consider its recovery from few Fourier measurements. We formulate the problem in the Fourier domain and pose the recovery of G as the solution to the following structured low rank matrix completion problem.

min_{G} rank [T (G)] s . t b = A (G) + η

(8)

Here G is the data to be recovered. $T (G) \in C^{M \times N}$ is a structured Toeplitz matrix in the lifted domain. Since (8) is NP hard, we relax the rank function with a Schatten p(0 ≤ p ≤ 1) norm:

G^{⋆} = arg min_{G} ‖ T (G) ‖_{p} + \frac{λ}{2} ‖ A (G) - b ‖_{2}^{2}

(9)

where λ is a regularization parameter. Here, ∥X∥_p is the Schatten p norm, defined as $‖ X ‖_{p} ≔ \frac{1}{p} Tr [(X^{*} X)^{\frac{p}{2}}] = \frac{1}{p} \sum_{i} σ_{i}^{p}$ , where σ_i are the singular values of X. p = 1 results in a convex nuclear norm penalty and when (0 ≤ p < 1), the Schatten norm is non-convex. When p → 0, ∥X∥₀ ≔ ∑_i log σ_i.

Note that we lift the original problem involving a 3-D signal to a large matrix $T (G)$ , whose number of rows is around three times the total number of pixels in the 3-D volume. The number of columns is equal to the size of the filter. The explicit use of such a matrix requires a lot of memory for storage and also increases the computational complexity of the problem. Even for a data set of dimension 128 × 128 × 15 and filter size of 21 × 21 × 3, the memory demand is 1323 times the memory needed to store the original signal, which makes the application of the scheme to even modest sized datasets intractable.

4. OPTIMIZATION ALGORITHM

We use an iterative re-weighted least squares (IRLS) algorithm [11] to solve (9), which relies on the property $‖ X ‖_{p} = ‖ X H^{\frac{1}{2}} ‖_{F}^{2}$ , where $H = (X^{*} X)^{\frac{p}{2} - 1}$ . Setting $X = T (G)$ , we obtain the iterative algorithm that alternates between the following steps:

H_{n} = [T (G_{n - 1})^{*} T (G_{n - 1}) + ϵ_{n} I]^{\frac{p}{2} - 1}

(10)

G_{n} = arg min_{G} ‖ T (G) H_{n}^{\frac{1}{2}} ‖_{F}^{2} + \frac{λ}{2} ‖ A (G) - b ‖_{2}^{2}

(11)

where ϵ_n → 0 is added to stabilize the inverse. We now show how the above steps can be modified to avoid the explicit evaluation and storage of the large lifted matrix $T (G)$ .

4.1. Update of G_n

Denoting H = [h₁, .., h_N], we rewrite (11) as

G^{*} = arg min_{G} \frac{1}{2} \sum_{i = 1}^{N} ‖ T (G) h_{i} ‖_{F}^{2} + \frac{λ}{2} ‖ A (G) - b ‖_{2}^{2}

(12)

By exploiting the structure of $T (G)$ and from the commutative property of convolution we have,

T (G) h_{i} = P_{Λ_{2}} (Q (G) * h_{i}) = P_{Λ_{2}} (h_{i} * Q (G)) = {PC}_{i} Q (G)

(13)

Here, * denotes 3-D convolution. $Q$ is a linear operator specified by $Q = [Q_{x}^{*}, Q_{y}^{*}, α Q_{z}^{*}]^{*}$ . Here, $Q (G)$ represents element wise multiplication of G by Fourier derivatives j2πk_x, j2πk_y and j2πk_z where k = (k_x, k_y, k_z). C_i represents the 3-D linear convolution by h_i. $P_{Λ_{2}}$ is the projection of the convolution onto a valid k space index set Λ₂ and is represented by the matrix P.

We approximate C_i by a 3-D circular convolution by h_i, which is valid if the convolution grid is sufficiently large. This allows us to evaluate C_i as ${FD}_{i} F^{*}$ , where F is the 3-D DFT matrix and D_i is a diagonal matrix corresponding to the 3-D inverse DFT of h_i. We also assume $P^{*} P \approx I$ , which is valid if the projection set Λ₂ is large compared to the filter size. Substituting (13) in (12) and then taking the gradient, we obtain

\underset{R}{\underset{︸}{(Q^{*} F \underset{D (\bar{μ})}{\underset{︸}{(\sum_{i = 1}^{N} D_{i}^{*} D_{i})}} F^{*} Q + λ A^{*} A)}} G = λ A^{*} b

(14)

where $D (\bar{μ})$ is a diagonal matrix with entries

\bar{μ} (r) = \sum_{i = 1}^{N} ∣ μ_{i} (r) ∣^{2}, \forall (r) \in [0, 1]^{3}

(15)

Here, μ_i(r) is a trigonometric polynomial corresponding to the inverse fourier transform of h_i. With these approximations, forming matrix vector products with R only requires 2 FFT’s after precomputing $\bar{μ}$ .

4.2. Updating $\bar{μ} (r)$ using (10)

Using the convoution relation mentioned in (13), the correlation matrix $R = T (G)^{*} T (G)$ can be computed as

R \approx P_{Λ_{1}} [C (Q (G))^{*} C (Q (G))] P_{Λ_{1}}^{*}

(16)

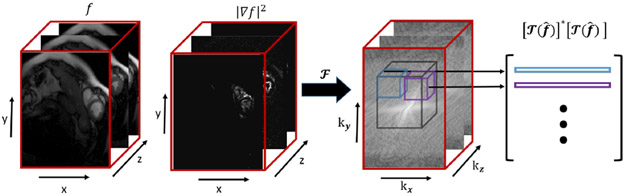
where $P_{Λ_{1}}$ is the projection onto the set Λ₁, C is applied to each block of $Q (G)$ and represents circular convolution. By expressing C in terms of the DFT matrix F, we can simplify (16) further and obtain $R \approx P_{Λ_{1}} [{FDF}^{*}] P_{Λ_{1}}^{*}$ where D is a diagonal matrix whose entries correspond to $∣ \nabla ∣^{2} ≔ (∣ \frac{\partial \tilde{G}}{\partial_{x}} ∣^{2} + ∣ \frac{\partial \tilde{G}}{\partial_{y}} ∣^{2} + ∣ \frac{\partial \tilde{G}}{\partial_{z}} ∣^{2})$ . Hence the entries of R are obtained from the Fourier coefficients of ∣∇∣²; specifically every row of R is obtained by vectorizing a brick shaped region of size equal to the dimensions of the filter from the black cuboid region of dimension twice the size of the filter. See Fig. 2 which depicts the construction of R.

Fig. 2: — Illustration of the direct evaluation of $T (G)^{*} T (G)$ that does not require the lifting. This direct computation, as well as the update step (14) that does not require the lifted matrix, results in the fast and memory efficient algorithm for (9).

Next the weight matrix H can be efficiently computed from the eigen decomposition of R. Let (V, Λ) be the eigen decomposition of $T (G)^{*} T (G)$ , where V is the orthogonal basis of eigen vectors v_i and Λ is a diagonal matrix containing the eigen values λ_i. Substituting the eigen decomposition in (10) and simplifying further we obtain,

H = [V (Λ + ϵ I) V^{*}]^{\frac{p}{2} - 1} = V (Λ + ϵ I)^{\frac{p}{2} - 1} V^{*} .

Hence, one choice of the matrix square root $H^{\frac{1}{2}}$ is

H^{\frac{1}{2}} = V (Λ + ϵ I)^{\frac{p}{4} - \frac{1}{2}} = [α_{1}^{\frac{1}{2}} v_{1}, \dots, α_{N}^{\frac{1}{2}} v_{N}] .

where $α_{i} = (λ_{i} + ϵ)^{\frac{p}{2} - 1}$ . The spatial domain trigonometric polynomial μ_i and v_i are related as $μ_{i} = α_{i}^{\frac{1}{2}} γ_{i} (r)$ where γ_i(r) is the inverse fourier transform of the eigen vector v_i. Hence using this relation, the SOS polynomial is updated as

\bar{μ} (r) = \sum_{i = 1}^{N} α_{i} ∣ γ_{i} (r) ∣^{2}, \forall (r) \in [0, 1]^{3}

(17)

which can be efficiently computed using N FFT’s. Note that the weights α_i are only high for vectors v_i close to the null space.

5. EXPERIMENTS AND RESULTS

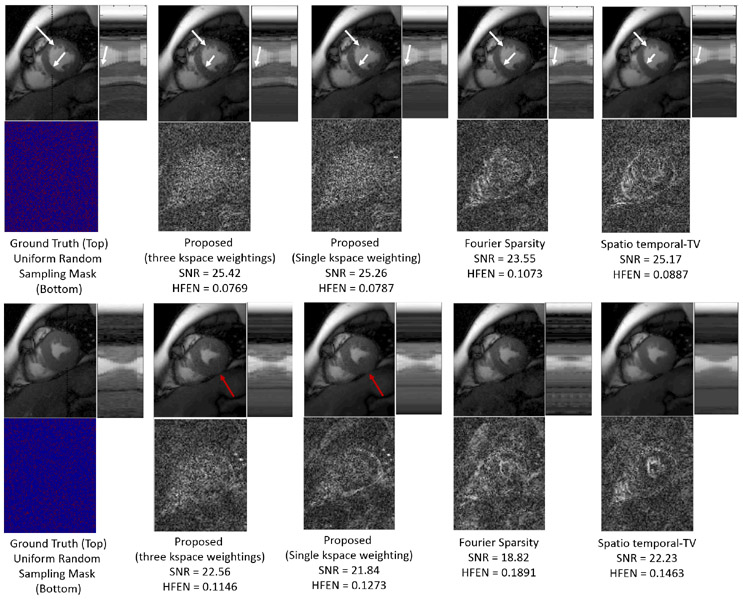
In Fig 3, we compare the recovery of the proposed method (single weighting and multiple weighting) with the spatio-temporal TV (S-TV) and temporal Fourier Sparsity (FS) regularized reconstruction methods on a Breath Held Cine Data of dimension (224 × 256 × 16 × 5) (coil compressed) at an acceleration factor of four and seven respectively. The data was acquired using a SSFP sequence using the following parameters: TE/TR= 2.0/4.1 ms and flip angle=45°. For the proposed method, a filter size of (21 × 21 × 3) was used in the recovery.

$Q$ is defined as ${\sqrt{(j ω_{x})^{2} + (j ω_{y})^{2} + (α j ω_{z})}}^{_{2}}$ for the proposed method with single kspace weighting. As this is an isotropic operator, at an acceleration factor of seven, it results in a recovery with some edges blurred, compared to the proposed method with multiple weightings and TV. The reconstructions from the proposed method with multiple weightings are more accurate with a lot of details faithfully captured. Specifically, the errors corresponding to it are scattered as opposed to being concentrated along the edges, which is the case with TV and Fourier sparsity based methods.

6. CONCLUSION

We introduced a fast & memory efficient algorithm to recover piecewise smooth three dimensional signals from few of their measurements. The algorithm is similar in concept to iterative reweighted algorithm for total variation regularization, with the exception that the weights are derived using a novel Fourier domain strategy involving singular value decomposition. The ability of the scheme to additionally regularize the smoothness of the edges enables it to provide improved results over total variation regularization. The comparison of the proposed scheme against state of the art methods in the context of cine MRI demonstrates its ability to provide more accurate reconstructions with better edge details.

Acknowledgments

This work is supported by NIH 1R01EB019961-01A1

7. REFERENCES

[1].Jin KH, Lee D, and Ye JC, “A general framework for compressed sensing and parallel MRI using annihilating filter based low-rank hankel matrix,” arXiv preprint arXiv:1504.00532, 2015. [Google Scholar]
[2].Haldar JP, “Low-rank modeling of local k-space neighborhoods (loraks) for constrained mri.” Medical Imaging, IEEE Transactions on, vol. 33, no. 3, pp. 668–681, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
[3].Ongie G and Jacob M, “Super-resolution MRI using finite rate of innovation curves,” IEEE International Symposium on Biomedical Imaging (ISBI), April 2015. [Google Scholar]
[4].—, “Recovery of piecewise smooth images from few fourier samples,” in Sampling Theory and Applications (SampTA), May 2015, pp. 543–547. [Google Scholar]
[5].Pan H, Blu T, and Dragotti PL, “Sampling curves with finite rate of innovation,” Signal Processing, IEEE Transactions on, vol. 62, no. 2, 2014. [Google Scholar]
[6].Ongie G and Jacob M, “A fast algorithm for stuctured low rank matrix recovery with applications to undersampled MRI reconstruction,” ISBI, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
[7].—, “Recovery of piecewise smooth images from few Fourier samples,” SampTA, 2015. [Google Scholar]
[8].Vetterli M, Marziliano P, and Blu T, “Sampling signals with finite rate of innovation,” Signal Processing, IEEE Transactions on, vol. 50, no. 6, pp. 1417–1428, 2002. [Google Scholar]
[9].Liang Z-P, Haacke E, and Thomas C, “High-resolution inversion of finite fourier transform data through a localised polynomial approximation,” Inverse Problems, vol. 5, no. 5, p. 831, 1989. [Google Scholar]
[10].Ongie G and Jacob M, “A fast algorithm for structured low-rank matrix recovery,” IEEE International Symposium on Biomedical Imaging (ISBI), April 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
[11].Mohan K and Fazel M, “Iterative reweighted algorithms for matrix rank minimization,” The Journal of Machine Learning Research, vol. 13, no. 1, pp. 3441–3473, 2012. [Google Scholar]

[R1] [1].Jin KH, Lee D, and Ye JC, “A general framework for compressed sensing and parallel MRI using annihilating filter based low-rank hankel matrix,” arXiv preprint arXiv:1504.00532, 2015. [Google Scholar]

[R2] [2].Haldar JP, “Low-rank modeling of local k-space neighborhoods (loraks) for constrained mri.” Medical Imaging, IEEE Transactions on, vol. 33, no. 3, pp. 668–681, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R3] [3].Ongie G and Jacob M, “Super-resolution MRI using finite rate of innovation curves,” IEEE International Symposium on Biomedical Imaging (ISBI), April 2015. [Google Scholar]

[R4] [4].—, “Recovery of piecewise smooth images from few fourier samples,” in Sampling Theory and Applications (SampTA), May 2015, pp. 543–547. [Google Scholar]

[R5] [5].Pan H, Blu T, and Dragotti PL, “Sampling curves with finite rate of innovation,” Signal Processing, IEEE Transactions on, vol. 62, no. 2, 2014. [Google Scholar]

[R6] [6].Ongie G and Jacob M, “A fast algorithm for stuctured low rank matrix recovery with applications to undersampled MRI reconstruction,” ISBI, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R7] [7].—, “Recovery of piecewise smooth images from few Fourier samples,” SampTA, 2015. [Google Scholar]

[R8] [8].Vetterli M, Marziliano P, and Blu T, “Sampling signals with finite rate of innovation,” Signal Processing, IEEE Transactions on, vol. 50, no. 6, pp. 1417–1428, 2002. [Google Scholar]

[R9] [9].Liang Z-P, Haacke E, and Thomas C, “High-resolution inversion of finite fourier transform data through a localised polynomial approximation,” Inverse Problems, vol. 5, no. 5, p. 831, 1989. [Google Scholar]

[R10] [10].Ongie G and Jacob M, “A fast algorithm for structured low-rank matrix recovery,” IEEE International Symposium on Biomedical Imaging (ISBI), April 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R11] [11].Mohan K and Fazel M, “Iterative reweighted algorithms for matrix rank minimization,” The Journal of Machine Learning Research, vol. 13, no. 1, pp. 3441–3473, 2012. [Google Scholar]

PERMALINK

ACCELERATED DYNAMIC MRI USING STRUCTURED LOW RANK MATRIX COMPLETION

Arvind Balachandrasekaran

Greg Ongie

Mathews Jacob

Abstract

1. INTRODUCTION

2. THEORY

Fig. 1:

3. PROPOSED FORMULATION

3.1. Measurement Model

3.2. Problem formulation

4. OPTIMIZATION ALGORITHM

4.1. Update of G_n

4.2. Updating $\bar{μ} (r)$ using (10)

Fig. 2:

5. EXPERIMENTS AND RESULTS

Fig. 3:

6. CONCLUSION

Acknowledgments

7. REFERENCES

ACTIONS

PERMALINK

RESOURCES

Cite

Add to Collections

PERMALINK

ACCELERATED DYNAMIC MRI USING STRUCTURED LOW RANK MATRIX COMPLETION

Arvind Balachandrasekaran

Greg Ongie

Mathews Jacob

Abstract

1. INTRODUCTION

2. THEORY

Fig. 1:

3. PROPOSED FORMULATION

3.1. Measurement Model

3.2. Problem formulation

4. OPTIMIZATION ALGORITHM

4.1. Update of Gn

4.2. Updating μ¯(r) using (10)

Fig. 2:

5. EXPERIMENTS AND RESULTS

Fig. 3:

6. CONCLUSION

Acknowledgments

7. REFERENCES

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

4.1. Update of G_n

4.2. Updating $\bar{μ} (r)$ using (10)