Abstract
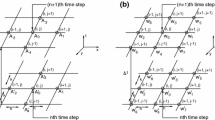
In this paper, we extend a previous work on a compact scheme for the steady Navier–Stokes equations [Li, Tang, and Fornberg (1995), Int. J. Numer. Methods Fluids, 20, 1137–1151] to the unsteady case. By exploiting the coupling relation between the streamfunction and vorticity equations, the Navier–Stokes equations are discretized in space within a 3×3 stencil such that a fourth order accuracy is achieved. The time derivatives are discretized in such a way as to maintain the compactness of the stencil. We explore several known time-stepping approaches including second-order BDF method, fourth-order BDF method and the Crank–Nicolson method. Numerical solutions are obtained for the driven cavity problem and are compared with solutions available in the literature. For large values of the Reynolds number, it is found that high-order time discretizations outperform the low-order ones.
Similar content being viewed by others
REFERENCES
Ascher, U., Ruuth, S. J., and Wetton, B. T. R. (1995). Implicit-explicit methods for timedependent partial differential equations. SIAM J. Numer. Anal. 32, 797–823.
Ascher, U., and Petzold, L. R. (1998). Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations, SIAM, Philadelphia.
Chen, G. Q., Gao, Z., and Yang, Z. F. (1993). A perturbation h4 exponential finite difference scheme for the convective diffusion equation. J. Comput. Phys. 104, 129–139.
Chudanov, V. V., Popkov, A. G., Churbanov, A. G., Vabishchevich, P. N, and Makarov, M. M. (1995). Operator-splitting schemes for the stream function-vorticity formulation.Comput. Fluids 24, 771–786.
Dennis, S. C. R, and Hudson, J. D. (1989). Compact h4 finite-difference approximations to operators of Navier-Stokes type. J. Comput. Phys. 85, 390–416.
E, W. (2001). Numerical methods for viscous incompressible flows: some recent advances. In Proceedings of Workshops in Scientific Computing Hong Kong '99, Z.-C. Shi et al. (eds.), Science Press, to appear.
E, W., and Liu, J.-G. (1996). Essentially compact schemes for unsteady viscous incom-pressible flows. J. Comput. Phys. 126, 122–138.
E, W., and Liu, J.-G. (1996). Vorticity boundary condition and related issues for finite difference schemes. J. Comput. Phys. 124, 368–382.
Ghia, U., Ghia, K. N., and Shin, C. T. (1982). High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method. J. Comput. Phys. 48, 387–411.
Gupta, M.M. (1991). High accuracy solutions of incompressible Navier-Stokes equations. J. Comput. Phys. 93, 343–359.
Goodrich, J. W., and Soh, W. Y. (1989). Time-dependent viscous incompressible Navier-Stokes equations: The finite difference galerkin formulation and streamfunction algorithms. J. Comput. Phys. 84, 207–241.
Gresho, P.M. (1992). Some interesting issues in incompressible fluid dynamics, both in the continuum and in numerical simulation. Adv. Appl. Mech. 28, 45–140.
Gupta, M. M., and Manohar, R. P. (1979). Boundary approximations and accuracy in viscous flow computations. J. Comput. Phys. 31, 265–288.
Hairer, E., Norsett, S. P., and Wanner, G. (1993). Solving Ordinary Differential Equations, Springer, Berlin-New York, 2nd ed.
Hou, T. Y., and Wetton, B. T. R. (1992). Convergence of a finite difference scheme for the Navier-Stokes equations using vorticity boundary conditions. SIAM J. Numer. Anal. 29, 615–639.
Huang, H., and Seymour, B. R. (1996). The no-slip boundary condition in finite difference approximations. Int. J. Numer. Methods Fluids 22, 713–729.
Huang, H., and Seymour, B. R. (2000). Finite difference solutions for incompressible flow problems with corner singularities. J. Sci. Comput. 15, 265–292.
Li, M., Tang, T., and Fornberg, B. (1995). A compact fourth-order finite difference scheme for the steady incompressible Navier-Stokes equations. Int. J. Numer. Methods Fluids 20, 1137–1151.
Roache, P. J. (1972). Computational Fluid Dynamics, Hermosa Publishers, Albuquerque, New Mexico.
Saad, Y., and Schultz, M. H. (1986). GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7, 856–869.
Strikwerda, J. C. (1997). High-order-accurate schemes for incompressible viscous flow. Int. J. Numer. Methods Fluids 24, 715–734.
Thom, A. (1933). The flow past circular cylinder at low speeds. Proc. Roy. Soc. London (Ser. A) 141, 651–666.
Woods, L. C. (1954). A note on the numerical solution of fourth order differential equa-tions. Aeronaut. Quart. 5, 176–184.
Wu, J. Z., and Wu, J.M. (1996). Vorticity dynamics on boundaries. Adv. Appl. Mech. 32, 119–275.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Li, M., Tang, T. A Compact Fourth-Order Finite Difference Scheme for Unsteady Viscous Incompressible Flows. Journal of Scientific Computing 16, 29–45 (2001). https://doi.org/10.1023/A:1011146429794
Issue Date:
DOI: https://doi.org/10.1023/A:1011146429794