Large Deformation Diffeomorphic Metric Curve Mapping

Joan Glaunès; Anqi Qiu; Michael I Miller; Laurent Younes

doi:10.1007/s11263-008-0141-9

. Author manuscript; available in PMC: 2010 Apr 22.

Published in final edited form as: Int J Comput Vis. 2008 Dec 1;80(3):317–336. doi: 10.1007/s11263-008-0141-9

Large Deformation Diffeomorphic Metric Curve Mapping

Joan Glaunès ¹, Anqi Qiu ^2,^✉, Michael I Miller ³, Laurent Younes ⁴

PMCID: PMC2858418 NIHMSID: NIHMS188687 PMID: 20419045

Abstract

We present a matching criterion for curves and integrate it into the large deformation diffeomorphic metric mapping (LDDMM) scheme for computing an optimal transformation between two curves embedded in Euclidean space ℝ^d. Curves are first represented as vector-valued measures, which incorporate both location and the first order geometric structure of the curves. Then, a Hilbert space structure is imposed on the measures to build the norm for quantifying the closeness between two curves. We describe a discretized version of this, in which discrete sequences of points along the curve are represented by vector-valued functionals. This gives a convenient and practical way to define a matching functional for curves. We derive and implement the curve matching in the large deformation framework and demonstrate mapping results of curves in ℝ² and ℝ³. Behaviors of the curve mapping are discussed using 2D curves. The applications to shape classification is shown and experiments with 3D curves extracted from brain cortical surfaces are presented.

Keywords: Large deformation, Diffeomorphisms, Vector-valued measure, Curve matching

1 Introduction

Matching curves embedded in ℝ² and ℝ³ is important in the fields of medical imaging and computer vision (Zhang 1994; Besl and McKay 1992; Feldmar and Ayache 1996). In medical imaging, the most striking gross morphological features of the cerebral cortex are the sulcal fissures on the cortical surface (Welker 1990). They are selected as the basis for structural analysis on the internal surface anatomy of the brain because they separate functionally distinct regions and provide a natural topographic partition of the anatomy. Even though major sulci consistently appear in all anatomies, they exhibit variability in size and configurations (Welker 1990). A quantitative study of sulcal anatomical structures requires developing mathematical models for characterizing shape and geometry of curves, and for accommodating the variability present across populations (Durrleman et al. 2007; Fillard et al. 2007; Thompson et al. 1996; Rettmann et al. 2002). Moreover, image boundary, contours, and skeletons are often used to represent shapes of objects in many applications of computer vision, such as tracking human body motion in motion tracking, finding correspondence between maps and terrain images, object recognition and classification. All of these formulate two problems: representation of curves and mathematical models of transformations.

In non-rigid registration problems, desired transformations are often constrained to be diffeomorphic—one to one (invertible) and smooth with smooth inverse so that connected sets remain connected, disjoint sets remain disjoint, smoothness of features such as curves is preserved, and coordinates are transformed consistently. Consequently, many researchers have paid great attention to such diffeomorphic transformations particularly in the field of Computational Anatomy for studying the geometric variation of human anatomy (e.g. Grenander and Miller 1998; Gee and Bajcsy 1999; Miller et al. 2002; Twining et al. 2002; Beg et al. 2005; Joshi et al. 2004; Avants and Gee 2004; Thompson and Toga 1996; Thompson et al. 2004).

Over the past several years we have been using large deformation diffeomorphic metric mapping (LDDMM) (Joshi and Miller 2000; Camion and Younes 2001; Beg et al. 2005) to map 3D volume coordinates in the brain as well as in the heart (Helm et al. 2006). This method not only provides a diffeomorphic correspondence φ between shapes C and S, but defines a metric distance in a shape space as well. The basic diffeomorphic metric mapping approach taken for understanding structures of object shapes is to place the set of objects into a metric space. The idea is to model the mapping of one from the other via a dynamic flow of diffeomorphisms (time dependent deformation) t ∈ [0, 1] of the ambient space ℝ^d. Instead of working directly in the space of diffeomorphisms, we work with time dependent vector fields, υ_t : ℝ^d → ℝ^d for t ∈ [0, 1], which model the infinitesimal efforts of the flow. The flow $φ_{t}^{υ}$ is then defined via the differential equation

\frac{\partial φ_{t}^{υ}}{\partial t} = υ_{t} (φ_{t}^{υ}),

(1)

with $φ_{0}^{υ} (x) = x$ , and the resulting diffeomorphism is given by the flow at time t = 1, $φ_{1}^{υ}$ . In order to ensure that the resulting solution to this equation is a diffeomorphism, υ_t must belong to a space, V, of regular vector fields (see Trouvé 1995; Dupuis et al. 1998 for specific requirements), for t ∈ [0, 1] with $\int_{0}^{1} ‖ υ_{t} ‖_{V} dt < \infty$ . V is a Hilbert space with an associated kernel function k_V, and norm ‖·‖_V. This norm models the infinitesimal cost of the flow.

Assume that for any pair objects of C and S, there exists some vector fields υ_t such that the diffeomorphism $φ_{1}^{υ}$ transforms shape C to shape S, which we write $φ_{1}^{υ} \cdot C = S$ . Then one can look at the optimal vector fields υ̂_t satisfying $φ_{1}^{\hat{υ}} \cdot C = S$ and minimizing the integral of the infinitesimal costs. The metric distance between shapes, ρ(C, S), is defined as the length of the geodesic path $φ_{1}^{\hat{υ}} \cdot C$ for t ∈ [0, 1] generated from C to S in the shape space. Such a metric between C and S has the form

\begin{matrix} ρ (C, S) = inf_{υ_{t}} {(\int_{0}^{1} {‖ υ_{t} ‖}_{V}^{2} dt)}^{\frac{1}{2}} \\ such that φ_{1}^{υ} \cdot C = S . \end{matrix}

(2)

In practice, we often define an inexact matching problem: find a diffeomorphism φ̂_t between two objects C and S as a minimizer of

J_{C, S} (φ_{t}) \dot{=} γ ρ {(C, φ_{1} \cdot C)}^{2} + E (φ_{1} \cdot C, S) .

Equivalently, we have ${\hat{φ}}_{t} = φ_{t}^{\hat{υ}}$ , where the vector fields υ̂_t minimize the energy

J_{C, S} ({(υ_{t})}_{t \in [0, 1]}) \dot{=} γ \int_{0}^{1} {‖ υ_{t} ‖}_{V}^{2} dt + E (φ_{1}^{υ} \cdot C, S),

(3)

and γ is a trade-off parameter. The first term in (3) is a regularization term to guarantee the smoothness of deformation fields and the second term is a matching functional to quantify the mismatching between the objects $φ_{1}^{υ} \cdot C and S$ .

In this LDDMM framework, two matching techniques are commonly used that result in different models for $E (φ_{1}^{υ} \cdot C, S)$ . The first one is volume image matching, which works directly with the raw 3D volume images, multi-valued vectors, as well as tensor matrices arising from DTI studies (Beg 2003; Beg et al. 2005; Cao et al. 2005a, 2005b), but is computationally intensive. The second one is landmark matching which requires a manual or semi-automated selection of landmarks on the images (Joshi and Miller 2000). In the case of brain images, however, landmarks are usually not just isolated points, but lie along sulcal or gyral curves extracted from cortical surfaces which are themselves segmented from the 3D images. In such a situation, the landmark matching tool is commonly used (Joshi et al. 2007; Bakircioglu et al. 1999). It is imperfect, however, because it first requires to select the same number of points on both source and target curves, and second it specifies arbitrary correspondences between specific points on these curves, giving artificial constraints to the registration process. To overcome this issue, some new methods were proposed, e.g. using level-sets representations of the curves (Leow et al. 2004). In Glaunès et al. (2004), an extension of the LDDMM approach in which shapes are considered as unlabelled sets of landmarks has been proposed. However, as geometric objects, curves or surfaces should not be treated as a sequences of points because the higher order information (tangent vectors or curvature) is discarded when reducing 1D or 2D manifolds into 0-dimensional point sets. In the case of surfaces, a representation via currents, or vector-valued measures, has recently been developed (Vaillant and Glaunès 2005). It allows to put into the metric both location and tangential information of the surfaces. Tools presented in Glaunès et al. (2004) and Vaillant and Glaunès (2005) actually derive from the same general framework that defines computable metrics on any m-dimensional submanifolds of ℝ^d with m ≤ d. The case of curves (m = 1) has been introduced shortly in Glaunès et al. (2006), Qiu et al. (2007). It is the purpose of this paper to present a full mathematical explanation and derivation of this representation of curves in the LDDMM framework.

This model for curve matching is a special case of a general framework for submanifolds, which could be called measure or current matching, and uses ideas from geometric measure theory and reproducing kernels while setting up into Grenander’s theory of deformable templates (Grenander and Miller 1998). Other examples had already been presented: surfaces in Vaillant and Glaunès (2005) and unlabelled point sets (which correspond to the 0-dimensional case) in Glaunès et al. (2004). In particular, the study and use of the metric distance defined in the shape space for shape analysis has received great attention in computer vision and medical imaging as partly shown here in Sect. 5. The common approach consists in defining a Riemannian metric on the tangent space to a curve, i.e. the space of infinitesimal transformations of a curve, and extending it to the whole space. Sharon and Mumford (2006) proposed a very elegant mathematical model for closed planar curves, which can not be generalized. Younes (1998) proposed to use an elastic metric that measures the cost of deformation of the ambient space, which corresponds to the LDDMM setting described previously and considered in the present paper. Recent works (Klassen et al. 2003; Mio and Srivastava 2004; Schmidt et al. 2006) have emphasized the efficiency of the shape space model or developed its mathematical theory (Michor and Mumford 2007). However these constructions require that a smooth transformation actually exists between any two curves in the space, which usually restricts the study to the subclass of closed, non crossing curves. Our approach is different in the sense that we do not claim to find exact correspondences between curves, but rather find a diffeomorphic transformation that match two curves up to an acceptable error. What we propose here is a way to compute this error, i.e. a model for evaluating the differences between shapes that remain after matching. It allows to compare curves that may present noisy parts, or be composed of different numbers of connected components, or to match a closed curve to an open curve, etc. Such situations are common in practical applications, which indicates that the curve mapping presented in this paper will be more suitable to applications in computer vision and medical imaging analysis.

This paper is organized as follows. We start with the geometric representation of curves that incorporates the geometry of the curves due to the sensitivity to both location and their tangent vectors (the first order local geometric structure) in Sect. 2.1. In Sect. 2.2, we describe that such a representation of curves as mathematical objects provide elements in a vector space equipped with a computable normed distance. In Sect. 3, “closeness” between two curves is then quantified by the norm-square distance between their associated representations, which serves as matching criterion for finding an optimal transformation from one curve to the other. In Sect. 3.2, we integrate this matching functional with a variational optimization problem of the LDDMM and compute its gradient with respect to a linear transformation of the velocity, momentum. Appendix B, demonstrates the other use of the matching functional in the derivation of the similarity transformation (rotation, translation, and isotropic scaling). In Sect. 5, we finally demonstrate the application of this method to curves in ℝ² and ℝ³ and compare matched results and deformation fields between this method and the landmark matching method (Joshi and Miller 2000) in the LDDMM framework.

2 Curves as Vector-Valued Measures

We define a norm that quantifies the similarity between two curves by first introducing a geometric representation of the curve and then inducing its norm in a Hilbert space via a differential operator.

2.1 Geometric Curve Representation

We follow the approach presented (Vaillant and Glaunès 2005) for surfaces. However, we will not use the term “currents” in this paper, nor use any notion of exterior calculus. Let C ⊂ ℝ^d be an open or closed curve. We assume that C is both piecewise C⁰ and piecewise C¹, which means that it may be composed of several disconnected components, and may present a finite number of angular points. Let γ_C : [0, 1] → ℝ^d, s ↦ γ_C(s) = [x¹(s), …, x^d (s)] be a parametrization of this curve. At almost any point on the curve, the tangent vector is given by $γ_{C}^{'} (s) = [\frac{{dx}^{1}}{ds}, \dots, \frac{{dx}^{d}}{ds}]$ . The existence of these tangent vectors along the curve gives us a natural action of the curve on vector fields w : ℝ^d → ℝ^d by the rule:

〈 µ_{C} | w 〉 \dot{=} \int_{0}^{1} γ_{C}^{'} (s) \cdot w (γ_{C} (s)) ds,

(4)

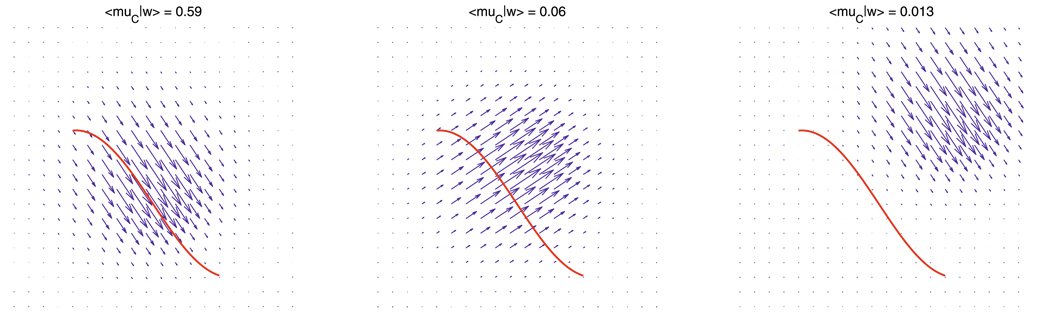
where · denotes the dot product in ℝ^d. Intuitively, 〈µ_C|w〉 is large when the direction of the vector field w(x) is close to the tangent vectors $γ_{C}^{'} (s)$ along the curve. It is close to zero when w(x) is almost perpendicular to the curve, or when w(x) take small values (in norm) along the curve. Figure 1 demonstrates the evaluation of 〈µ_C|w〉 in several cases when w(x) is parallel to the tangents of C (first panel), perpendicular to C (middle panel), and the norm of w(x) is close to zero along the curve (last panel).

Fig. 1 — Evaluation of a vector field (*blue arrows*), w(x), along a curve (*in red*), C. *Left*: Directions of vectors match those of the tangents to the curve. *Middle*: Directions are perpendicular to the curve. *Right*: Directions match, but norm of vectors are close to zero along the curve

Hence both location and tangential information of the curve is integrated in this expression. Another important point here is that it is invariant under re-parametrization of the curve, so that if we have a new parameter t = ψ(s), with ψ increasing, it is simple to show that 〈µ_C|w〉 is unaffected. However using t = ψ(s) with ψ decreasing will give an opposite value for 〈µ_C|w〉, which means that the representation is orientation dependent.

Equation (4) associates to every oriented curve C a unique representant µ_C which is a linear functional acting on vector fields of ℝ^d. Equivalently, µ_C can be understood as a vector-valued Borel measure. Linear combinations of measures are defined with the rule 〈αµ_C + βµ_S|w〉 = α 〈µ_C|w〉 + β 〈µ_S|w〉 for any α, β ∈ ℝ and curves C, S. In general, these combinations are not associated to any curve, unless |α| = |β| = 1: for example, µ_C − µ_S corresponds to the concatenation of curve C and curve S with opposite orientation.

The advantage here is to embed the curves in a vector space (of vector-valued measures) on which it is possible to use functional analysis tools to define norms and compare curves via these norms. This will be developed in Sect. 2.2.

2.2 Norm on Vector-Valued Measure

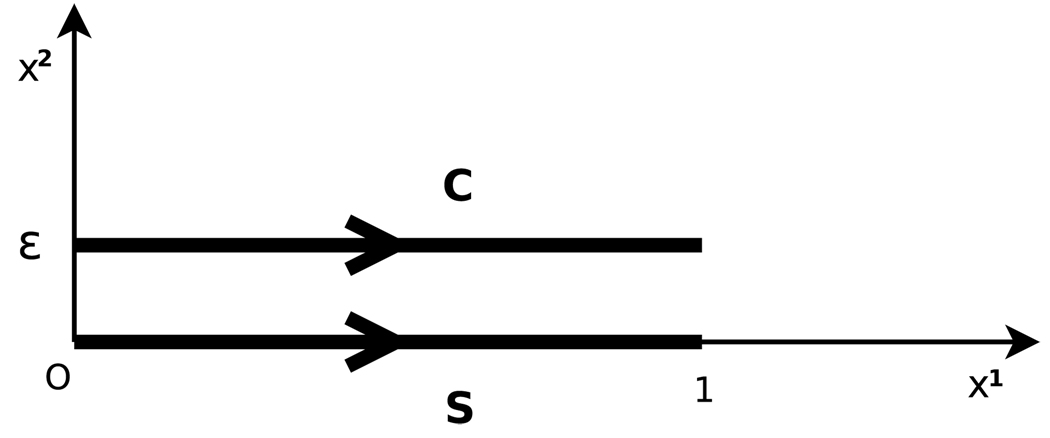
We would like to define a norm that computes a geometrical distance between two curves. For instance, Fig. 2 shows two parallel segments C and S with length 1 in ℝ², separated by a small distance ε. We want the norm of the difference µ_C − µ_S of the corresponding vector-valued measures to be small since the segments are close to each other.

This can be achieved if one puts constraints on the variations of the test vector fields w so that the evaluation of the curve representors µ_C and µ_S on w gives close results. To do so, we define a norm on vector fields in the form of

{‖ w ‖}_{w}^{2} \dot{=} \int_{ℝ^{d}} {| L w (x) |}^{2} dx,

(5)

where L is a linear differential operator of sufficient order such that the following property on the norm is guaranteed

\begin{matrix} {‖ w ‖}_{1, \infty} & = \sup_{x \in ℝ^{d}} {| w (x) | + \sum_{i = 1}^{d} | \frac{\partial w}{\partial x^{i}} (x) |} \\ \leq c_{W} {‖ w ‖}_{W} \end{matrix}

(6)

for some fixed constant c_W > 0. In this setting, test vector fields w will belong to the Hilbert space W associated with the norm ‖·‖_W.

Proposition 1

If property in (6) is satisfied, then the linear functional µ_C defined in (4) is a continuous linear functional on W.

Proof For any w ∈ W,

\begin{matrix} | 〈 µ_{C} | w 〉 | & \leq \int_{0}^{1} | γ_{C}^{'} (s) \cdot w (γ_{C} (s)) | ds \\ \leq \int_{0}^{1} | γ_{C}^{'} (s) | | w (γ_{C} (s)) | ds \\ \leq {‖ w ‖}_{1, \infty} \int_{0}^{1} | γ_{C}^{'} (s) | ds = {‖ w ‖}_{1, \infty} l_{C} \\ \leq c_{W} {‖ w ‖}_{W} l_{C}, \end{matrix}

where l_C is the length of C.

We can therefor compare vector-valued measures via the dual norm, defined by:

{‖ µ_{C} ‖}_{W^{*}} \dot{=} \sup_{{‖ w ‖}_{W} \leq 1} 〈 µ_{C} | w 〉 .

Going back to example of Fig. 2, the evaluation of the difference µ_C − µ_S is

\begin{matrix} 〈 µ_{S} - µ_{C} | w 〉 = & \int_{0}^{1} γ_{S}^{'} (s) \cdot w (γ_{S} (s)) \\ - γ_{C}^{'} (s) \cdot w (γ_{C} (s)) ds . \end{matrix}

With γ_S(s) = (s, 0), γ_C(s) = (s, ε), $γ_{C}^{'} (s) = γ_{S}^{'} (s) = (1, 0)$ , we get

〈 µ_{S} - µ_{C} | w 〉 = \int_{0}^{1} (w^{1} (s, 0) - w^{1} (s, ε)) ds,

where w¹(s, 0) denotes the first coordinate of vector w(s, 0). The integrand w¹(s, 0) − w¹(s, ε) is bounded by ε ‖w‖_1,∞, which in turn is bounded by εc_W ‖w‖_W from property (6). Hence the dual norm ‖µ_S − µ_C‖_W* is bounded by εc_W. When ε decreases, the norm ‖µ_C − µ_S‖_W* goes to zero, as expected.

2.3 Explicit Expression of the Dual Norm with Kernels

The explicit expression of the dual norm involves the Green’s function k_W(x, y) of the operator L*L, where L* is the adjoint of L. k_W(x, y) is also the reproducing kernel of the space W. It is defined by the property

\begin{matrix} \int_{ℝ^{d}} {Lk}_{W} (x, y) ξ \cdot Lw (y) dy & = {〈 k_{W} (x, \cdot) ξ, w 〉}_{W} \\ = w (x) \cdot ξ, \end{matrix}

(7)

where 〈·, · 〉_W represents the inner product of two vector fields in Hilbert space W. Note that since we are dealing with vector fields, k_W(x, y) is a matrix operator, we need to apply it to a vector ξ ∈ ℝ^d to get a proper definition.

To fix ideas at this point, one may choose L such that L*L = (Id − α²∇²)^k for some constants α > 0 (scale parameter) and integer k, which gives the Sobolev H_k Hilbert space. The corresponding kernel operator has explicit expression in terms of modified Bessel functions of the second kind (McLachlan and Marsland 2007).

Lemma 1

The norm of the vector-valued measure µ_C in the dual space W* is equal to

\begin{matrix} {‖ µ_{C} ‖}_{W^{*}}^{2} = & \int_{0}^{1} \int_{0}^{1} [k_{W} (γ_{C} (s), γ_{C} (r)) γ_{C}^{'} (s)] \\ \cdot γ_{C}^{'} (r) ds dr . \end{matrix}

(8)

Proof

\begin{matrix} 〈 µ_{C} | w 〉 & = \int_{0}^{1} γ' (s) \cdot w (γ (s)) ds \\ = \int_{0}^{1} {〈 k_{W} (r (s), \cdot) γ' (s), w 〉}_{W} ds \\ = {〈 \int_{0}^{1} k_{W} (r (s), \cdot) γ' (s) ds, w 〉}_{W} . \end{matrix}

By Cauchy-Schwartz inequality, this achieves the maximum for ‖w‖_W = 1 if

w = \frac{\int_{0}^{1} k_{W} (γ (s), \cdot) γ' (s) ds}{{‖ \int_{0}^{1} k_{W} (γ (s), \cdot) γ' (s) ds ‖}_{w}} .

Therefore, we have

\begin{matrix} {‖ µ_{C} ‖}_{W^{*}}^{2} & = {‖ \int_{0}^{1} k_{W} (γ (s), \cdot) γ' (s) ds ‖}_{W}^{2} \\ = \int_{0}^{1} \int_{0}^{1} {〈 k_{W} (γ_{C} (s), \cdot) γ_{C}^{'} (s), k_{W} (γ_{C} (r), \cdot) γ_{C}^{'} (r) 〉}_{W} ds dr \\ \overset{(a)}{=} \int_{0}^{1} \int_{0}^{1} [k_{W} (γ_{C} (s), γ_{C} (r)) γ_{C}^{'} (s)] \\ \cdot γ_{C}^{'} (r) ds dr, \end{matrix}

where (a) follows from the reproducing property of the kernel k_W stated in (7).

The expression of the dual norm indicates that the central object in computations is the kernel k_W. Mathematically it is possible to build the Hilbert space W and its dual starting from a given positive kernel (without any knowledge of operator L), with enough regularity to satisfy the property in (6). Links between properties of the kernel and properties of the space in this setting can be found in Glaunès (2005). In short, k_W should be twice differentiable and vanish at infinity up to order 1. If one additionally requires invariance with respect to rigid motions, one can prove that k_W is defined by two scalar functions h, h^⊥ : ℝ⁺ → ℝ such that for every x, y ∈ ℝ^d, k_W(x, y)α = h(|x − y|²)α if α is colinear to x − y, and k_W(x, y)α = h^⊥(|x − y|²)α if α · (x − y) = 0. For our applications we only consider “scalar” kernels k_W(x, y) = h(|x − y|²)I_d i.e. such that h = h^⊥, and in practice we tried Gaussian $h (r^{2}) = e^{- r^{2} / σ_{W}^{2}}$ and Cauchy $h (r^{2}) = \frac{1}{1 + r^{2} / σ_{W}^{2}}$ kernels. However it would be interesting to study the effect of using non scalar kernels.

3 Curve Matching via Deformation Maps

3.1 A General Variational Formulation

In the previous section, we introduced representations of curves by vector-valued measures and defined a computable norm in the space of measures to compare them. These tools give us a practical way to define a matching functional between two curves C and S in ℝ^d. Let φ: ℝ^d → ℝ^d be a deformation map which is supposed to give an approximate correspondence between C and S. The accuracy of this matching can be measured by:

E (φ (C), S) \dot{=} {‖ µ_{φ (C)} - µ_{S} ‖}_{W^{*}}^{2}

(9)

which can be rewritten in terms of kernel k_W, according to (8),

\begin{matrix} E (φ (C), S) = & \int_{0}^{1} \int_{0}^{1} [k_{W} (γ_{φ (C)} (s), γ_{φ (C)} (r)) γ_{φ (C)}^{'} (s)] \\ \cdot γ_{φ (C)}^{'} (r) ds dr \\ - 2 \int_{0}^{1} \int_{0}^{1} [k_{W} (γ_{φ (C)} (s), γ_{S} (r)) γ_{φ (C)}^{'} (s)] \\ \cdot γ_{S}^{'} (r) ds dr \\ + \int_{0}^{1} \int_{0}^{1} [k_{W} (γ_{S} (s), γ_{S} (r)) γ_{S}^{'} (s)] \\ \cdot γ_{S}^{'} (r) ds dr . \end{matrix}

The first and last terms are intrinsic energies of the two curves. Roughly, the more curved they are, the higher energy they possess, since flat shaped parts of the curves tend to vanish in the space of vector-valued measures. The middle term penalizes to mismatching between tangent vectors of S and those of φ (C).

Optimal matching between curves will be defined via minimization of a functional composed of the matching term E and optionally a regularization term to guarantee smoothness of the transformations. We model deformation maps φ in the LDDMM framework. Certainly any other model of transformations could be directly applied at this point. For instance, the similarity transformation (rotation, translation, and uniform scale) is derived in Appendix B.

3.2 Large Deformation Diffeomorphic Metric Curve Mapping

In the LDDMM setting, we define the optimal matching, φ̂ between two curves C and S as $\hat{φ} = φ_{1}^{{\hat{υ}}_{t}}$ , υ̂_t being the minimizer of the energy

\begin{matrix} J_{C, S} ({(υ_{t})}_{t \in [0, 1]}) \dot{=} & γ \int_{0}^{1} {‖ υ_{t} ‖}_{V}^{2} dt \\ + {‖ µ_{φ_{1}^{υ} (C)} - µ_{S} ‖}_{W^{*}}^{2} \end{matrix}

(10)

and $φ_{1}^{υ}$ is defined in (1).

The first term is the regularization term which controls the smoothness of the diffeomorphism, and the second term is the data attachment to quantify mismatching between deformed C and S. A general result (Trouvé 1995; Dupuis et al. 1998) guarantees existence of the solution to this minimization problem.

In Glaunès et al. (2006), such variational problems for 2D curve matching in the large deformation framework were studied, and precise forms of the optimal solutions were given. In this paper we will focus on the discrete formulation, leading to a practical matching algorithm.

4 The Discrete Model

4.1 Representation with Vector-Valued Dirac Functionals

First suppose that the curve C is continuous and discretized in a sequence of points x = (x₁,…, x_n) such that each x_i belongs to the curve: for any parametrization γ_C we have x_i = x_si for s_i ∈ [0, 1]. We do not make any assumption on the way points x_i are distributed along the curve. If C is a closed curve then we assume x_n = x₁. We can associate to this sequence of points a specific measure given by vector-valued Diracs:

µ_{x} = \sum_{i = 1}^{n - 1} τ_{x, i} δ_{c_{x, i}},

where $c_{x, i} = \frac{1}{2} (x_{i} + x_{i + 1})$ is the center between points of x_i and x_i+1, and τ_x,i = x_i+1 − x_i gives an approximate tangent vector. This vector-valued measure is also defined by its pairing with smooth vector fields w:

〈 µ_{x} | w 〉 = \sum_{i = 1}^{n - 1} τ_{x, i} \cdot w (c_{x, i}) .

The important point here is that both the curves and their discrete representants (possibly with different sampling rates) are embedded into the same space of vector-valued measures. Hence it will be possible to compare them via the dual norm introduced earlier.

If C is piecewise continuous, we build a discrete representation by summing the discrete measures µ_x corresponding to each connected component.

4.2 Expression of the Dual Norm

The dual norm of the discrete representant µ_x expresses conveniently in terms of the kernel k_W:

\begin{matrix} {‖ µ_{x} ‖}_{W^{*}}^{2} & {= ‖ \sum_{i = 1}^{n} τ_{x, i} δ_{c_{x, i}} ‖}_{W^{*}}^{2} \\ = \sum_{i = 1}^{n} \sum_{j = 1}^{n} [k_{W} (c_{x, i}, c_{x, j},) τ_{x, i}] \cdot τ_{x, j} . \end{matrix}

(11)

Note that this is not an approximation of the dual norm, but an exact expression of the dual norm of the discrete approximation of the curve. The following theorem shows that this discrete representant is a good approximation of the curve in space W.

Theorem 1

If the length of the piece of curve connecting two consecutive points $d_{C} (x_{i}, x_{i + 1}) = \int_{s_{i}}^{s_{i + 1}} | γ_{C}^{'} (s) | ds$ is bounded by δ, then ‖µ_x − µ_C‖_W* ≤ c_Wδl_C.

Proof For any w ∈ W,

\begin{matrix} 〈 µ_{x} - µ_{C} | w 〉 & = 〈 µ_{x} | w 〉 - 〈 µ_{C} | w 〉 \\ = \sum_{i = 1}^{n} τ_{i} \cdot w (c_{i}) - \int_{0}^{1} γ_{C}^{'} (s) \cdot w (γ_{C}^{'} (s)) ds \\ = \sum_{i = 1}^{n} (τ_{i} \cdot w (c_{i}) \\ - \int_{s_{i}}^{s_{i + 1}} γ_{C}^{'} (s) \cdot w (γ_{C}^{'} (s)) ds) . \end{matrix}

We have $τ_{i} = γ_{C} (s_{i + 1}) - γ_{C} (s_{i}) = \int_{s_{i}}^{s_{i + 1}} γ_{C}^{'} (s) ds$ , so we can write:

\begin{matrix} 〈 µ_{x} - µ_{C} | w 〉 & = \sum_{i = 1}^{n} \int_{s_{i}}^{s_{i + 1}} γ_{C}^{'} (s) \cdot (w (c_{i}) - w (γ_{C}^{'} (s))) ds \\ \leq \sum_{i = 1}^{n} \int_{s_{i}}^{s_{i + 1}} | γ_{C}^{'} (s) | | w (c_{i}) - w (γ_{C}^{'} (s)) | ds . \end{matrix}

Now $| w (c_{i}) - w (γ_{C}^{'} (s)) | \leq | {‖ w ‖}_{1, \infty} | c_{i} - γ_{C}^{'} (s) | \leq c_{W} \cdot {‖ w ‖}_{W} δ$ , so we get

\begin{matrix} 〈 µ_{x} - µ_{C} | w 〉 & \leq c_{W} {‖ w ‖}_{W} δ \sum_{i = 1}^{n} \int_{s_{i}}^{s_{i + 1}} | γ_{C}^{'} (s) | ds \\ \leq c_{W} {‖ w ‖}_{W} δ l_{C} . \end{matrix}

4.3 Matching Functional, Discrete Case

When curves C and S are discretized by point sequences $x = {(x_{i})}_{i = 1}^{n} and y = {(y_{j})}_{j = 1}^{m}$ , the sequence of transformed points $z = {(φ (x_{i}))}_{i = 1}^{n}$ gives a discretization of the deformed curve φ(C). Here we will derive algorithms based on the following matching functional:

E (z, y) \dot{=} {‖ \sum_{i = 1}^{n} τ_{z, i} δ_{c_{z, i}} - \sum_{j = 1}^{m} τ_{y, j} δ_{c_{y, j}} ‖}_{W^{*}}^{2},

(12)

which is explicitly

\begin{matrix} E (z, y) = & \sum_{i = 1}^{n - 1} \sum_{j = 1}^{n - 1} [k_{W} (c_{z, i}, c_{z, j}) τ_{z, i}] \cdot τ_{z, j} \\ - 2 \sum_{i = 1}^{n - 1} \sum_{j = 1}^{m - 1} [k_{W} (c_{z, i}, c_{y, j}) τ_{z, i}] \cdot τ_{y, j} \\ + \sum_{i = 1}^{m - 1} \sum_{j = 1}^{m - 1} [k_{W} (c_{y, i}, c_{y, j}) τ_{y, i}] \cdot τ_{y, j} . \end{matrix}

Note that curves C and S are not necessarily discretized into the same number of points from the above equation. This expression was also given in Qiu et al. (2007). We show the derivation of gradient of E(z, y) with respect to φ in Appendix A.

4.4 LDDMM Variational Formulation in the Discrete Setting

Let $x = {(x_{i})}_{i = 1}^{n} and y = {(y_{i})}_{i = 1}^{m}$ be discrete samples of curves C and S respectively, and define the trajectories x_i(t) ≐ φ_t (x_i) for i = 1, …, n. The optimal matching between samples x and y will be defined as a minimizer of

J = γ \int_{0}^{1} {‖ υ_{t} ‖}_{V}^{2} dt + {‖ \sum_{i = 1}^{n} τ_{z, i} δ_{c_{z, i}} - \sum_{j = 1}^{m} τ_{y, j} δ_{c_{y, j}} ‖}_{W^{*}}^{2},

(13)

where $z = {(φ_{1} (x_{i}))}_{i = 1}^{n} = (x_{i} {(1))}_{i = 1}^{n}$ . The second term of J depends only on the positions of the finite number of points $(φ_{1} {(x_{i}))}_{i = 1}^{n}$ . In such a situation, like all point-based matching problems in the large deformation setting (Joshi and Miller 2000; Camion and Younes 2001), the following reasoning apply: starting from any arbitrary state υ̂_t of the time-dependent vector fields, let us find the optimal vector fields υ_t that keep trajectories $x_{i} (t) = φ_{t}^{{\hat{υ}}_{t}} (x_{i})$ unchanged and minimize the functional. Since trajectories are fixed, in particular the end-points (x_i (1)) are also fixed; hence the second term of J is constant for this sub-problem and we are left to find vector fields which minimize the V-norm and satisfy for each time t and each 1 ≤ i ≤ n the constraint υ_t (x_i (t))= ẋ_i (t) where x_i (t) are the fixed trajectories. This is a classical interpolation problem in a Hilbert space setting, for which the solution is expressed as a linear combination of spline vector fields involving the kernel operator k_V:

υ_{t} (x) = \sum_{i = 1}^{n} k_{V} (x_{i} (t), x) α_{i} (t),

(14)

where α_k(t) are referred to as momentum vectors. These vectors can be computed from trajectories x_i(t) by solving the system of linear equations

\frac{{dx}_{i} (t)}{dt} = \sum_{j = 1}^{n} k_{V} (x_{j} (t), x_{i} (t)) α_{j} (t), i = 1, \dots, n .

(15)

Now coming back to the main variational problem, we can restrict the domain of minimization to the subspace of vector fields of the form given by expression in (14), and choose either trajectories x_i(t) or momentum α_i(t) as minimization variables. The choice of α_i(t) avoids the inversion of linear systems, since in this case (15) is seen as an ODE system in the unknown x_i(t).

The regularization term can be rewritten as a function of variables α_i (t) and x_i (t). From (14) and the reproducing property of kernel k_V, we get

\begin{matrix} \int_{0}^{1} {‖ υ_{t} ‖}_{V}^{2} dt = \int_{0}^{1} \sum_{i = 1}^{n} \sum_{j = 1}^{n} {〈 k_{V} (x_{i} (t), \cdot) α_{i} (t), k_{V} (x_{j} (t), \cdot) α_{j} (t) 〉}_{V} dt \end{matrix}

(16)

\begin{matrix} = \int_{0}^{1} \sum_{i = 1}^{n} \sum_{j = 1}^{n} [k_{V} (x_{j} (t), x_{i} (t)) α_{j} (t)] \cdot α_{i} (t) dt \\ = \int_{0}^{1} \sum_{i = 1}^{n} α_{i} (t) \cdot \frac{{dx}_{i} (t)}{dt} dt . \end{matrix}

(17)

Hence the explicit expression of functional in (13) is the following:

\begin{matrix} J ((α_{i} (t))) = & γ \int_{0}^{1} \sum_{i = 1}^{n} \sum_{j = 1}^{n} [k_{V} (x_{j} (t), x_{i} (t)) α_{j} (t)] \cdot α_{i} (t) dt \\ + \sum_{i = 1}^{n - 1} \sum_{j = 1}^{n - 1} [k_{W} (c_{z, i}, c_{z, j}) τ_{z, i}] \cdot τ_{z, j} \\ - 2 \sum_{i = 1}^{n - 1} \sum_{j = 1}^{m - 1} [k_{W} (c_{z, i}, c_{y, j}) τ_{z, i}] \cdot τ_{y, j} \\ + \sum_{i = 1}^{m - 1} \sum_{j = 1}^{m - 1} [k_{W} (c_{y, i}, c_{y, j}) τ_{y, i}] \cdot τ_{y, j} . \end{matrix}

(18)

The derivation of the gradient of J with respect to α_i(t) is given in Appendix D.

4.5 Algorithm

We used a conjugate gradient routine to perform the minimization of functional J in (18) with respect to variables α_i (t). Of course any other optimization scheme could be considered at this point. The different steps required to compute the functional and its gradient for each iteration are the following:

from momentum vectors α_i (t), compute trajectories x_i (t) by integrating the system of ordinary differential equations (ODE) using (15)
evaluate J from (18)
compute vectors η_i (t) by integrating the system of ODE in (28) in Appendix D
compute gradient (∇J)_i (t) = 2γα_i (t)+ η_i (t).

All time-dependent variables were evaluated on a uniform grid t₁ = 0, …, t_T = 1 and a predictor/corrector centered Euler scheme was used to solve the systems of ODE in (15) and (28). The complexity of each iteration is of order dTN², where N = max(n, m). To speed up computations when N is large, all convolutions by kernels k_V and k_W are accelerated with a multipole method (Yang et al. 2003), which reduces the complexity to dTN log(N).

5 Results

In our experiments, we first used the similarity transformation to transform curves into the same orientation and scale, as described in Appendix B. Then, we applied the curve matching under the LDDMM setting to deform one curve to the other. Kernels of k_V (x, y) and k_W(x, y) were radial with the form $e^{- \frac{| y - x |^{2}}{σ^{2}}} I_{d}$ , where I_d is the d × d identity matrix. σ_V and σ_W represent the kernel sizes of k_V and k_W, respectively. They were experimentally adjusted.

5.1 2D Curve Matching

Examples

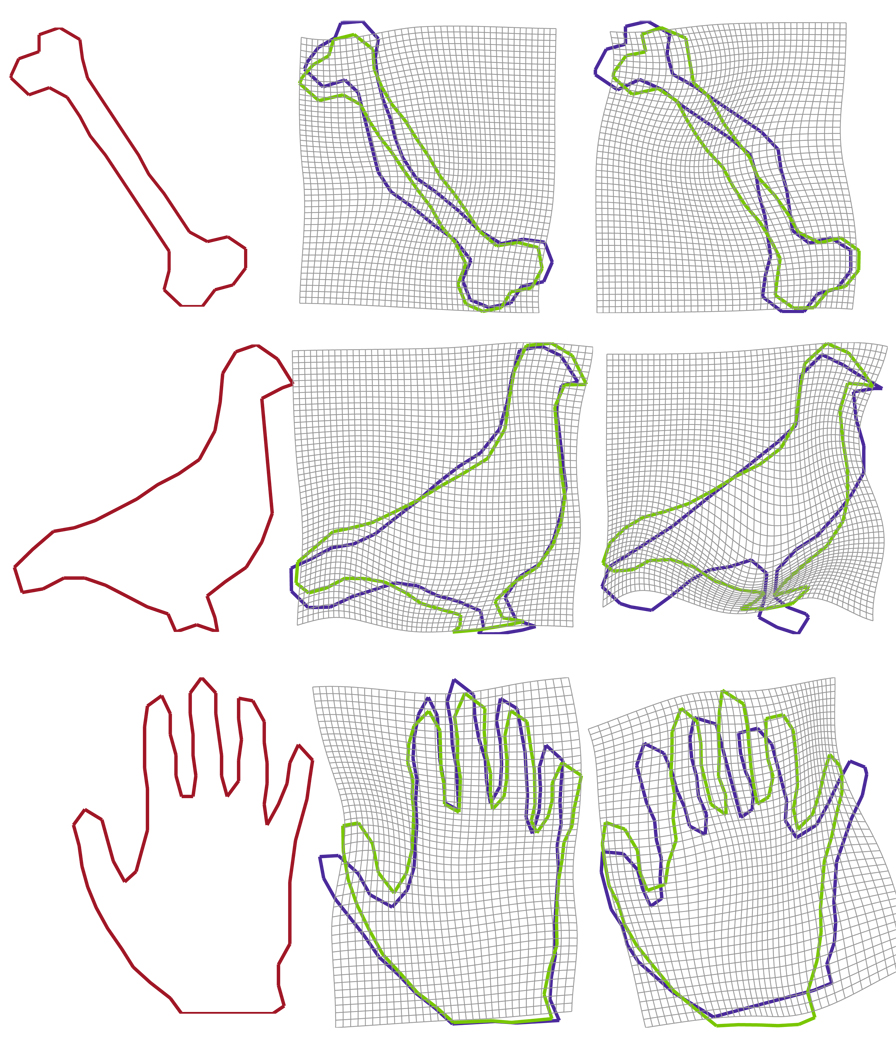
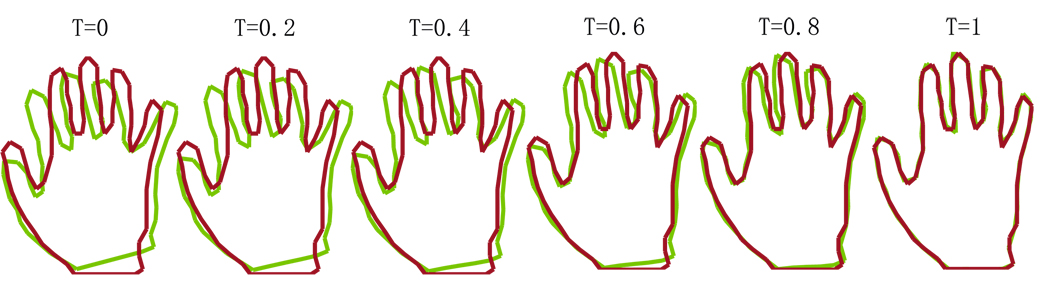
Shown in Fig. 3 are two-dimensional examples where the shape of curves represent bones (the first row), or birds (the second row), or hands (the third row). In this experiment, we chose σ_V = 0.25 and σ_W = 0.1 and deformed source shapes to target shapes. The first column shows the target shape, while the rest columns show source shapes. In each panel of the second and third rows, the blue curve represents the source shape before the curve matching and the green curve represents the deformed source shape after the curve matching. The background grid shows the deformation field. Figure 4 shows the time sequence of deformation of the source configuration. The first panel shows the source hand in green and the target hand in red. The last panel illustrates how close the deformed source curve (green) are to the target curve (red) after the curve matching. The middle panels demonstrate the smooth deformation as the source hand moves to the target hand along the time.

Fig. 4 — Panels from the *left* to the *right* depict the sequence of geodesic mappings connecting the source hand to the target hand at time t = 0, 0.2, 0.4, 0.6, 0.8, 1. The source shape and target shape are respectively represented in *green* and *red*

Robustness Against Noise

One application of studying transformations is to classify objects into different shape groups. In our LDDMM framework, the velocity vectors transform one object to the other object and give the shortest geodesic path connecting these two objects. The length of the geodesic path defines a metric distance given in (2) and feature in classification. As the purpose of classification, the metric distance should be robust against noise to achieve accurate classification. In this section, we claim that the curve matching provides a more accurate metric distance measurement and overcomes noise effect on matching results compared with the landmark matching (Joshi and Miller 2000; Allassonnière et al. 2005) when outliers are chosen as landmark points.

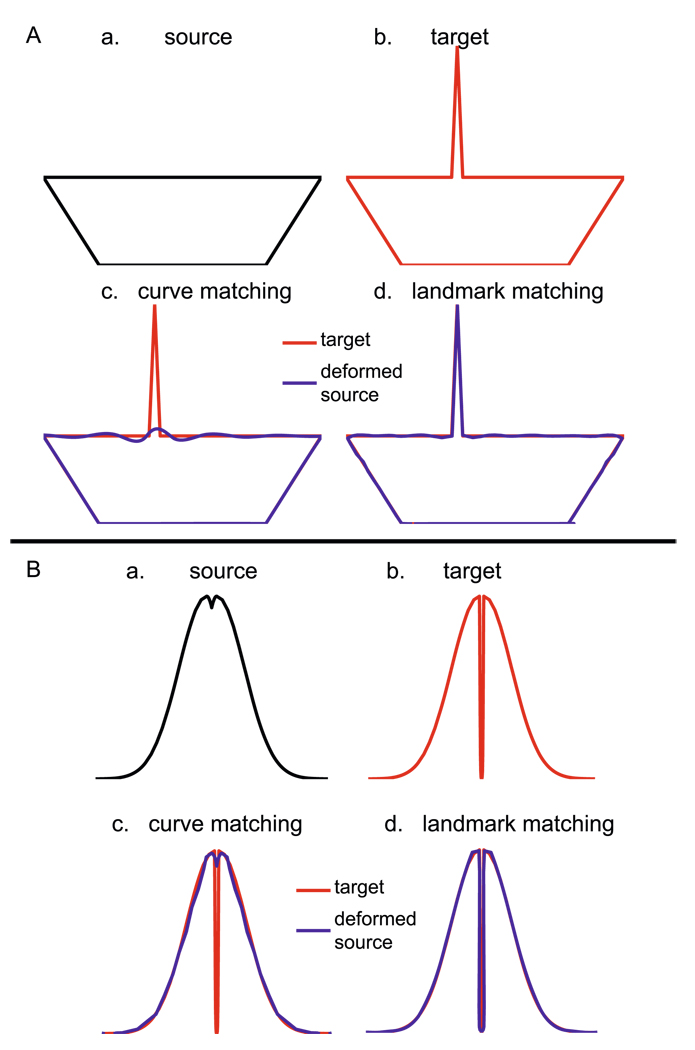
Example A in Fig. 5 shows boats without and with a mast as the source and target curves in panels (a, b), respectively. The curve and landmark matchings are applied to transforming the source boat to the target boat and results are shown in panels (c, d). The matching term in (18) for the template is near to zero in the region of the mast so that there is no force to drive the source boat to match the mast. The peak point of the mast is chosen as landmark in the landmark matching procedure so the source boat is deformed to the target boat at the mast. However, the metric distance (1.63) in the landmark matching is significantly larger than the one (0.13) in the curve matching. If a threshold is selected to classify these boats, the landmark matching probably considers them in different shape categories while the curve matching recognizes them as boats. When classifying shapes this problem typically arises as the result of imperfect extraction. The curve matching has less noise effect on the metric distance compared with the landmark matching. A similar example is given in Fig. 5(B), one curve without a gap (source shape) and the other with a small gap (target shape). The metric distance (1.37) in the landmark matching is larger than the one (0.72) in the curve matching.

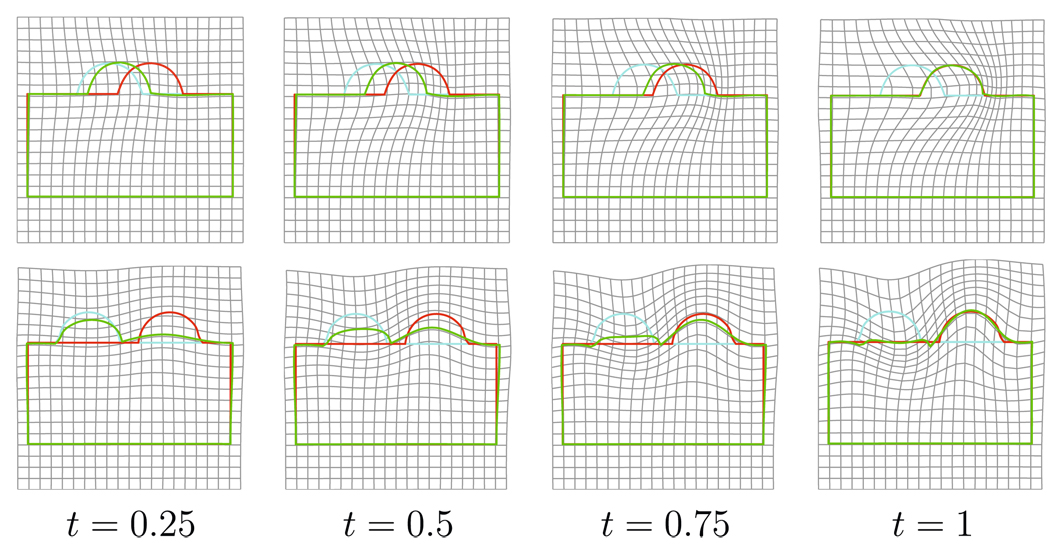
Box Bump Experiment

To study the behaviour of our curve matching algorithm, we computed matchings between two shapes (cyan and red curves in Fig. 6) composed of a box with a semi-circle. Each row in Fig. 6 shows one example representing the time evolution of the optimal diffeomorphism by green curve in each panel. The desired behaviour, in which the bump slides along the edge, occurs only when the bumps locations on the two shapes are close (see the top row of Fig. 6). Otherwise the deformation that flattens one bump and reforms the other one is prefered, because the deformation cost is lower (see the bottom row of Fig. 6). Note again that our algorithm matches shapes up to a small error, measured by the metric W*. Avoiding such solutions would require to put higher-order (typically curvature) information into the metric W*, while our metric only relies on tangential information.

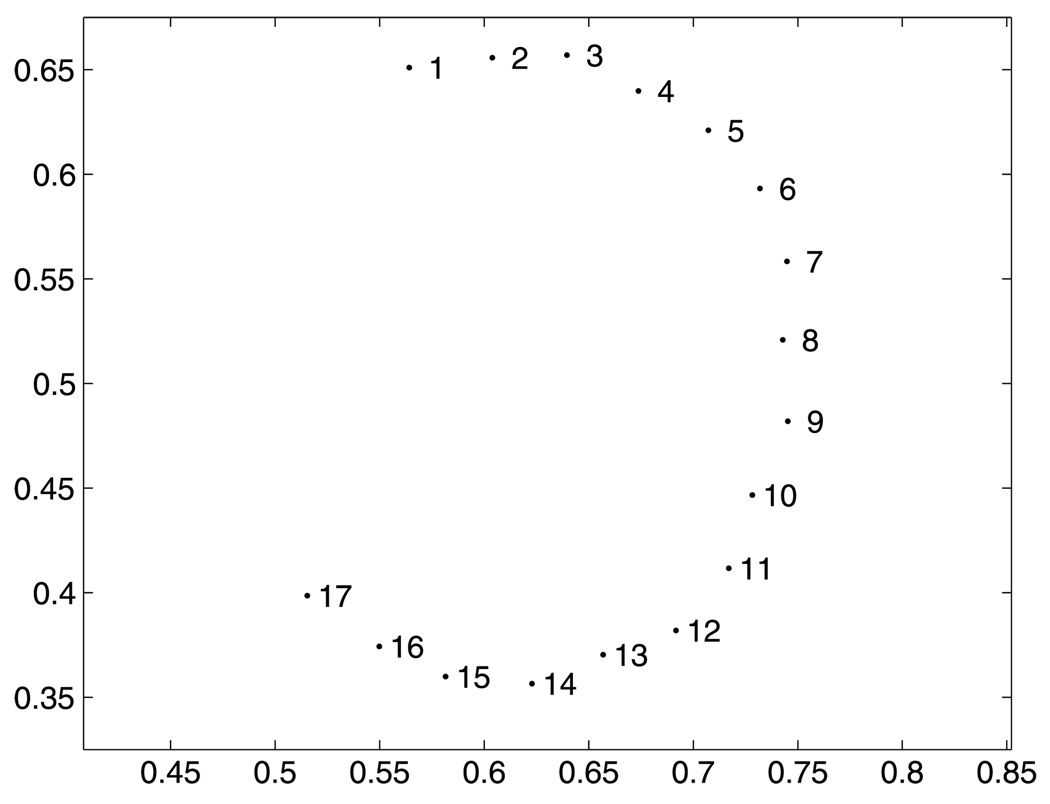
Computing all pairwise matchings between 17 shapes composed of a box with a semi-circle when the locations of the bump on each curve subsequently moves further away, we mapped the resulting distance matrix into a 2-dimensional coordinate system using classical multidimensional scaling (MDS) (Cox and Cox 2001). Figure 7 shows the locations of each shape in the first two scaling dimensions. This confirms the previous analysis: while shapes are correctly ordered into a sequence, they seem to follow a highly curved path, because the “flatten and reform” solutions bound the metric distances between shapes.

Classification

We demonstrate pattern classification of metric distances among curves shown in Fig. 8. The shapes in Fig. 8 were chosen from hand (10), dude (10), turtle (7), and fish (5). Special cases (hands and dudes with noise effect) are shown in the last two columns of rows (a, b), which are similar cases as in Fig. 5. The reason for choosing fish and turtles is that some of fish are outliers which are similar to turtles.

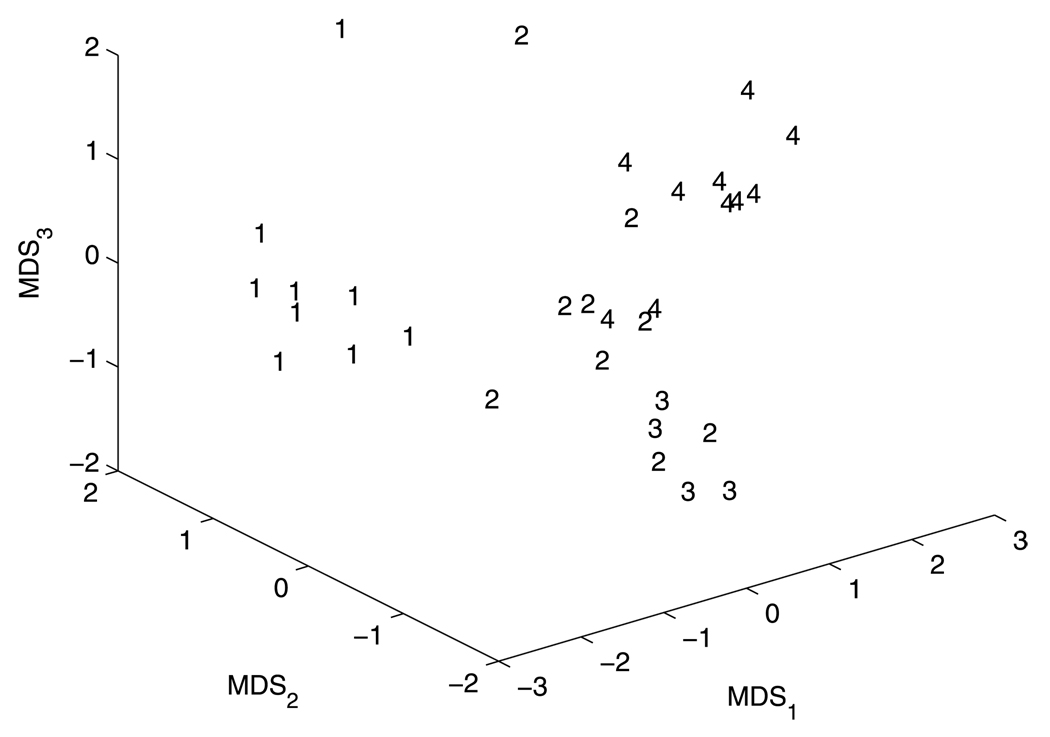
Our classification approach has three steps: map any two curves to each other and compute metric distances between them using (2), map metric distances into Euclidean space via MDS (Cox and Cox 2001), classify shapes via K-means clustering. Figure 9 shows the scatter plot of the curves in the features spaces generated from MDS. The numbers (1, 2, 3, 4) give the classification results and respectively denote the categories of hand, turtle, fish, and dude. Only two curves were wrongly classified as turtles. One is the hand shown in the second column from the right in row (a), the other is the fish shown in the last column of row (d). As we mentioned in the previous section, the small noise (e.g. the hand and dude in the last column of rows (a, b)) does not inference the classification using the curve matching approach. The successful performance rate of our classification approach is 93.75%.

Fig. 9 — A scatter plot of feature dimensions from multidimensional scaling. 1: hand, 2: turtle, 3: fish, 4: dude

5.2 3D Curve Matching

In this section, we illustrate matching results of 3D curves. All curves were extracted from brain cortical surfaces and matched to the template curve. For the purpose of visualization, we show deformed brain surfaces where the deformation fields obtained from the curve matching were interpolated.

Examples

One major application of the curve matching in medical imaging is to transform one anatomical structure to the other using anatomical curve information. For instance, curves in the brain anatomy can be sulci or gyri that are conventional boundaries of cortical regions. In this experiment, we demonstrate how to warp one cortical surface to the other using the curve matching method. Cortical surfaces shown in the following were generated from MRI image volumes. A 3D subvolume encompassing the region of interest (ROI) was defined manually in each volume. A Bayesian segmentation using the expectation-maximization algorithm to fit the compartmental statistics was used to label voxels in the subvolume as gray matter (GM), white matter (WM), or cerebrospinal fluid (CSF) (Joshi et al. 1999; Miller et al. 2000). Surfaces were then generated at the GM/WM interface using a topology-correction method and a connectivity-consistent isosurface algorithm (Han et al. 2001, 2002).

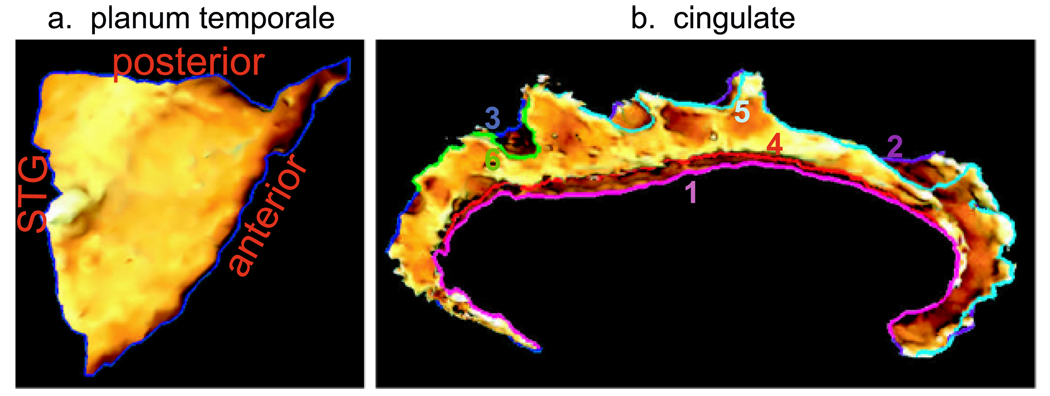
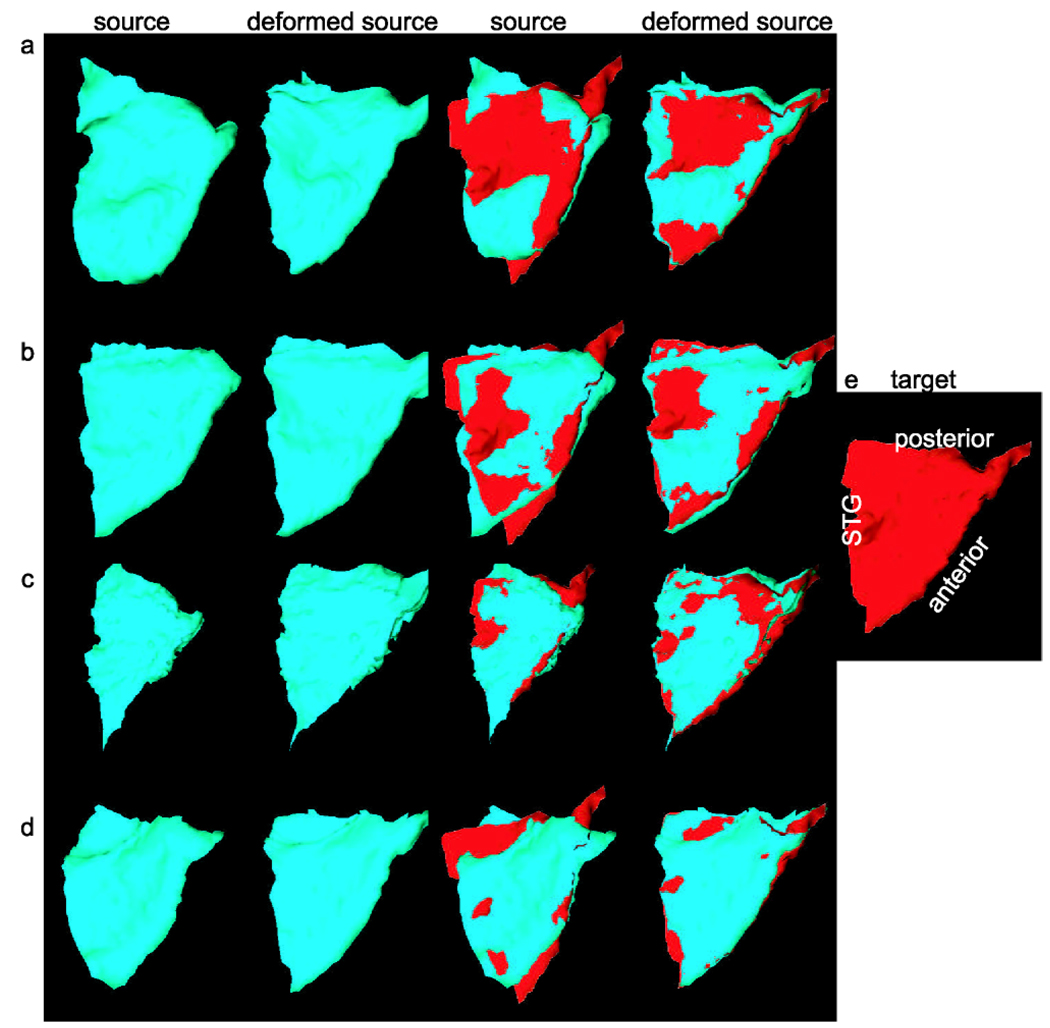
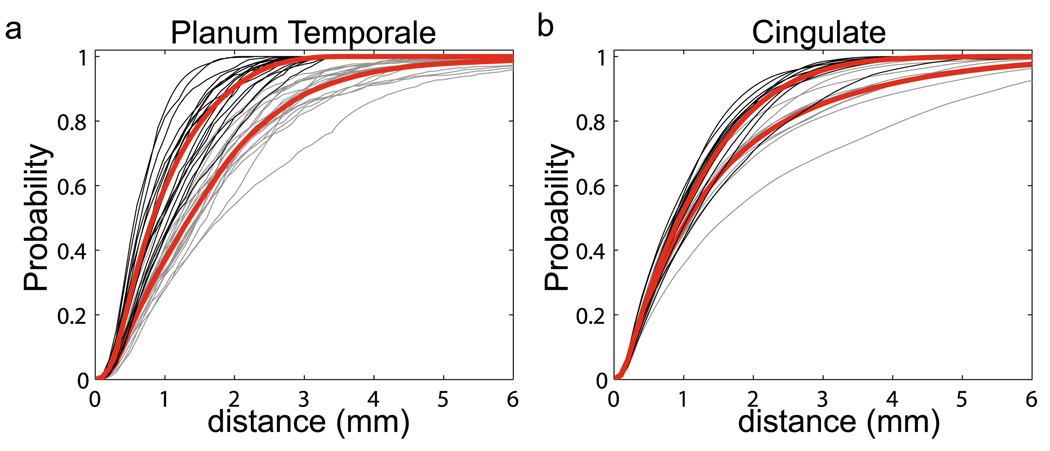
Figure 10(a) shows the target of planum temporale (PT) surface located on the superior temporal gyrus (STG) posterior to the Heschl’s sulcus (HS) and extending to Sylvian fissure (SF). The structure of PT can be determined by three principal curves (STG, HS, SF) tracked by dynamic programming (Ratnanather et al. 2003). In this experiment, we fixed one surface as the target PT surface shown in Fig. 10(a). We extracted the three curves from twenty PT surfaces as curve objects and registered them with the curves on the target curves using our curve matching algorithm. Finally, the deformation field was interpolated to the interior region of PTs. The columns from left to right on rows (a)–(d) in Fig. 11 respectively illustrate the source PT surface, deformed source PT, source PT superimposed with the target PT, and deformed source PT with the target PT. As shown in Fig. 11, the performance for this dataset was quite good. Panel (a) in Fig. 13 shows cumulative distance distributions before and after the matching process. The cumulative distance distribution plots the percentage of vertices whose distance to the target surface is less than d as a function of distance d. Gray curves correspond to the source surfaces, while black curves are for the deformed source surfaces after the matching. Red curves are the mean surface distance graphs before and after the matching process from the bottom to the top, respectively. It is obvious that more vertices move close to the target surface after the matching.

Fig. 10 — Panel (a) shows the curve defined as boundary curve for planum temporale cortical surface. Panel (b) depicts six curves describing the main shape of cingulate gyrus. Each curve is colored differently with indices in the same color scheme. The surfaces are colored by the curvature information

Fig. 11 — Three-dimensional deformation of planum temporale cortical surface. Panels (a)–(d) depict the deformation applied to planum temporale cortical surfaces. From the *left* to the *right*, panels respectively show the source and deformed source surfaces as well as the source and deformed source surfaces overlaying with the target surface in *red*. Panel (e) shows the target of planum temporale surface

Fig. 13 — Panels (a) and (b) depict the cumulative distance distributions for planum temporale and cingulate surfaces. The cumulative distance distributions for the source surfaces are in gray, while the distributions for the deformed source surface are in *black*. *Red curves* are the mean distributions for the source and deformed source surfaces

We applied the same strategy to match ten cingulate gyri (CG) to the target CG shown in panel (d) of Fig. 12. CG is a part of the limbic cortex and has functions related to symptoms of Schizophrenia and Alzheimer’s disease. Panel (b) in Fig. 10 shows the six curves defined on the target CG. Each curve is color coded with the index in the same color scheme. Panels (a)–(c) in Fig. 12 give examples of the source CG surfaces and their deformed versions. To validate the matched results, we also computed the cumulative distance distributions shown in panel (b) of Fig. 13. This set of the CG curve mapping results have been used to detect the group differences in the CG thickness between healthy comparison controls and patients with schizophrenia, which illustrated a successful application of the curve mapping in neuroimaging studies (Qiu et al. 2007).

Comparison with Landmark Matching

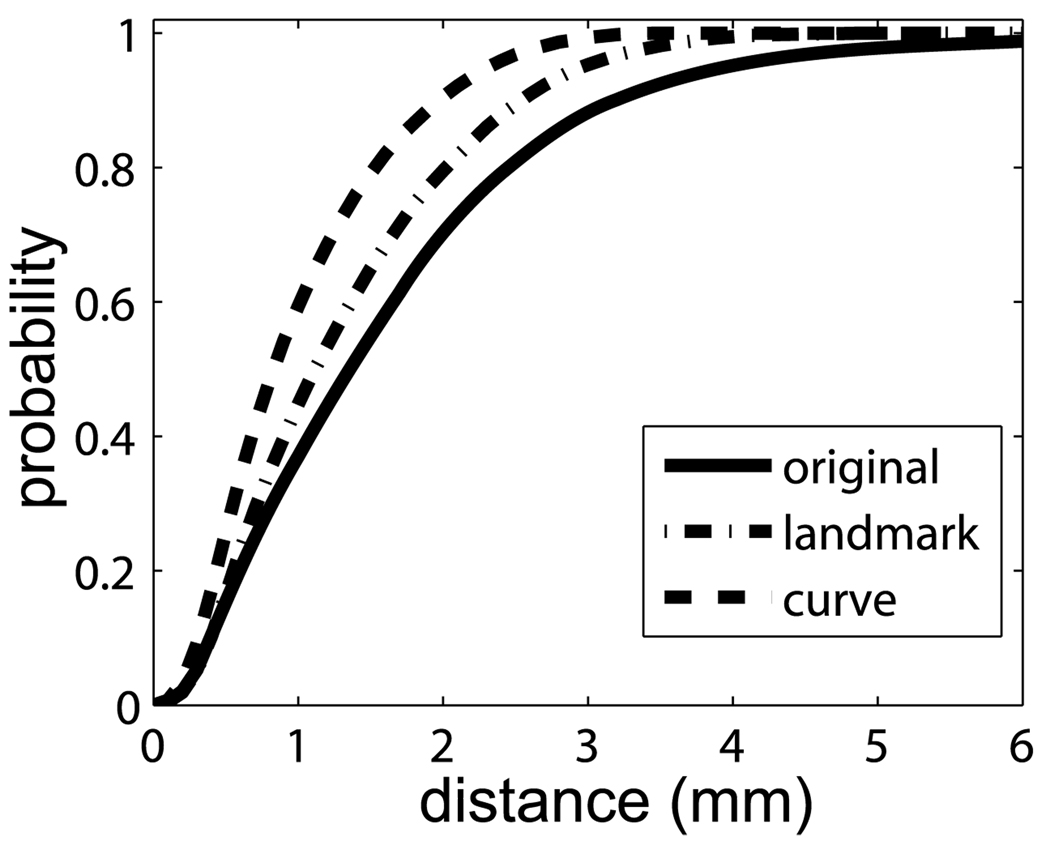
The first purpose of this section is to compare the matched results of PT surfaces via the curve matching algorithm with those from the landmark matching algorithm. Twenty PTs were used in this experiment. As for the PT structure, three corner points and three boundary curves of the PT are defined as point and curve objects across the population. In the landmark matching process, five points equally spaced on each boundary and the three corner points were chosen as point landmarks on each PT surface. Then, the landmark matching algorithm (Allassonnière et al. 2005; Joshi and Miller 2000) was applied to PTs to obtain the deformation field that was used to deform PT surfaces to the template. Since the PT structure is relatively flat and simple compared with other structures of the brain, the cumulative distance distribution between deformed source and target surfaces, as described in the previous section, can be used as quantitative validation measurement. Figure 14 shows the averages for the original source surfaces (solid line), deformed ones via the landmark matching (dashdot line), and deformed ones via the curve matching (dash line). This figure suggests that the cumulative distance distribution from the curve matching algorithm is above that from the landmark matching algorithm, which implies that the curve matching algorithm introduced here significantly improves matching results in terms of the surface distance measurement compared to those from the landmark matching method.

Fig. 14 — Comparison of the cumulative distance distributions between the landmark and curve matchings. *Solid*, *dashdot*, and *dash lines* represent average cumulative distance distributions over the original source, deformed source surfaces via the landmark and curve matchings, respectively

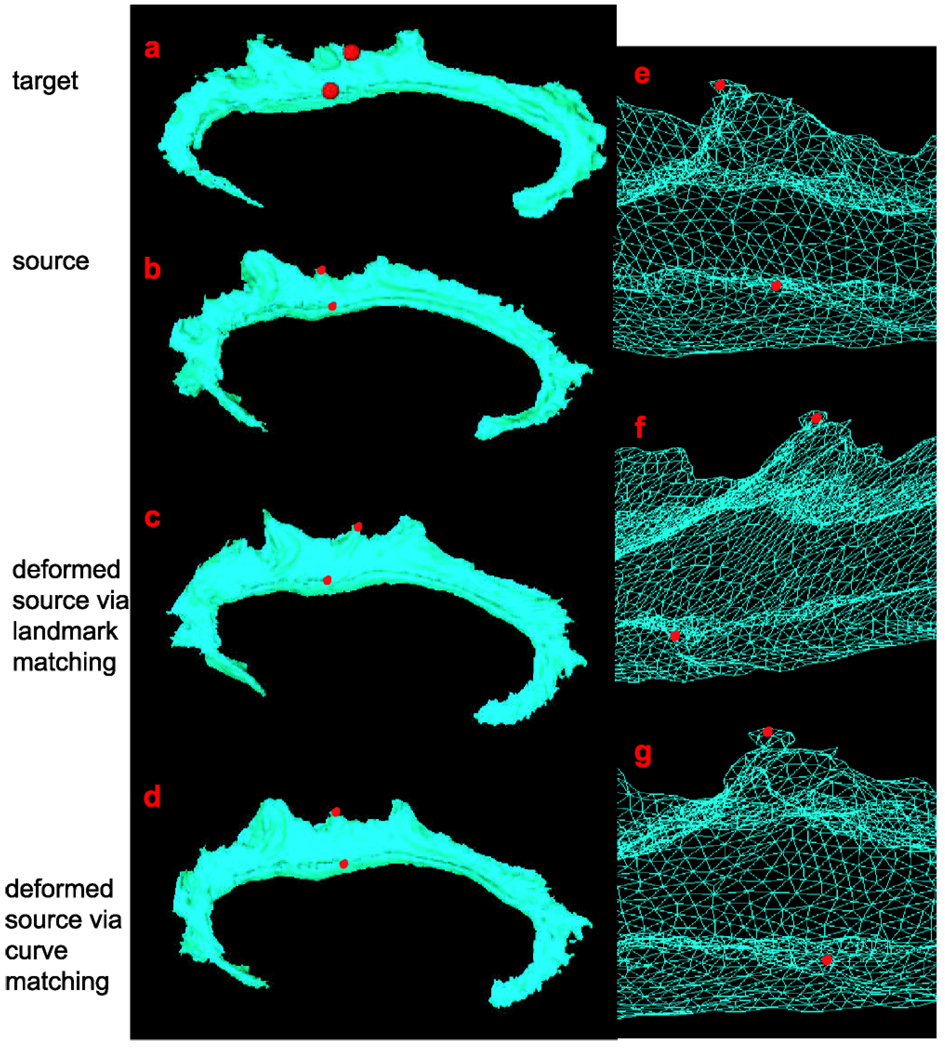
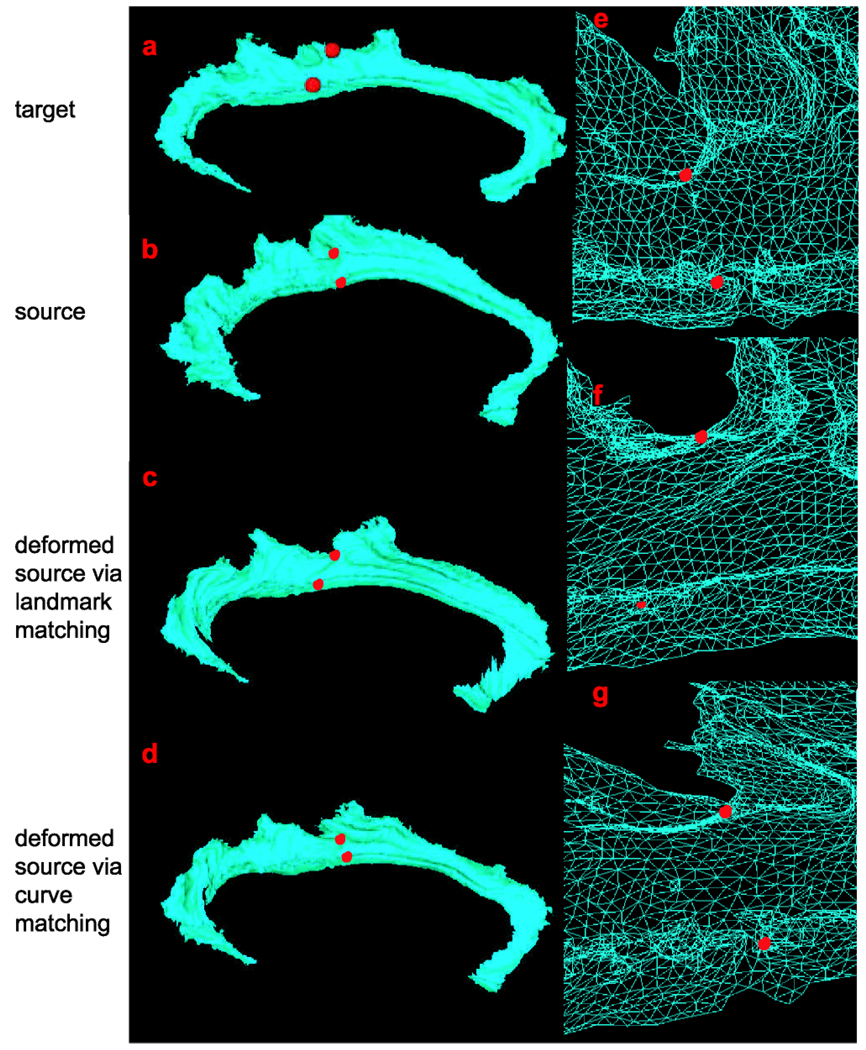
The second aim of this section is to compare deformation fields of CG surfaces from the landmark and curve matching algorithms. Landmark matching methods have been used to map curves and surfaces by extracting a pair labeled point sets from the curves as landmarks. However, manually labeling landmarks is labor-intensive as well as highly variable, and landmark matching methods are sensitive to the labeling. Consequently, it may result in giving incorrect mapping. In this experiment, we give such an example to show matching results and deformation fields via both landmark (Joshi and Miller 2000; Allassonnière et al. 2005) and curve matching methods under the LDDMM framework. In the landmark matching process, seventy two landmarks were selected from the six curves shown in panel (b) of Fig. 10, twelve landmarks per curve (Bakircioglu et al. 1998). After the landmark matching, the deformation field was interpolated for the other vertices on the CG. Figure 15 and Figure 16 give examples what the deformation fields are from the landmark and curve matchings. Panels (a)–(d) in both figures respectively show the target, source, deformed source CG surface after the landmark matching, and deformed source CG surface after the curve matching. Two red points are marked on the target surface in Figs. 15(a) and 16(a). Compared to the positions of these two points on the source surface, the relative positions are changed after the landmark matching process, which can be observed in panel (f) on both figures (zoom in version of the column in the triangulated mesh format). However, we do not observe such a change in the curve matching shown in panels (g) of Figs. 15 and 16. Thus, we conclude that the curve matching gives more proper deformation field due to incorporating the geometry information of the curves.

Fig. 15 — Comparison of deformation fields between the landmark and curve matchings. Panels (a–d) show the target, source, deformed source surface after the landmark matching, deformed source surface after the curve matching. *Red dots* represents paired landmarks on the target and source surfaces. Panels (e–g) show triangulated meshes respectively corresponding to the surfaces in panels (b–d)

Fig. 16 — Comparison of deformation fields between the landmark and curve matchings. Panels (a–d) show the target, source, deformed source surface after the landmark matching, deformed source surface after the curve matching. *Red dots* represents paired landmarks on the target and source surfaces. Panels (e–g) show triangulated meshes respectively corresponding to the surfaces in panels (b–d)

6 Conclusion

In this work we have proposed a mathematical framework in which both curves and their discrete samples are represented as vector-valued measures and embedded in a Hilbert space structure. Coupled with a model of deformations of the ambient space, we designed variational problems for curve matching takes convenient explicit formulations due to the use of the kernel of the Hilbert norm. We derived the case of the large deformations, given by integration of time-dependent vector fields. We also derived the case of the similitude transformation in Appendix B. We presented experiments for 2D and 3D curve mappings, and validated the accuracy of matching as well as demonstrated the behaviors of the curve mapping. Results indicate that the curve matching gives good matching and proper deformation fields compared to the landmark matching algorithm (Joshi and Miller 2000). We also proposed to apply this technique for shape classification using the metric distances provided by the large deformation framework.

Fig. 7 — 2-dimensional scaling plot of the distance matrix computed from pairwise matchings of 17 box bumps shapes

Acknowledgements

The work reported here was supported by grants: NIH P41 RR15241, NSF DMS 0456253, and National University of Singapore start-up grant R-397-000-058-133.

Appendix A: Gradient of E

As the first step, we compute the derivative of the dissimilarity measure between two sequences of points ${(z_{i})}_{i = 1}^{n} and {(y_{j})}_{j = 1}^{m}$ with respect to z, given in (19):

\begin{matrix} E = {‖ µ_{z} - µ_{y} ‖}_{W^{*}}^{2} = & \sum_{i = 1}^{n - 1} \sum_{j = 1}^{n - 1} [k_{W} (c_{z, i}, c_{z, j}) τ_{z, i}] \cdot τ_{z, j} \\ - 2 \sum_{i = 1}^{n - 1} \sum_{j = 1}^{m - 1} [k_{W} (c_{z, i}, c_{y, j}) τ_{z, i}] \cdot τ_{y, j} \\ + \sum_{i = 1}^{m - 1} \sum_{j = 1}^{m - 1} [k_{W} (c_{y, i}, c_{y, j}) τ_{y, i}] \cdot τ_{y, j} . \end{matrix}

Let 1 ≤ q ≤ n and z_q + εz̃_q be a small perturbation of point z_q ∈ ℝ^d, with other points fixed. Since $c_{z, i} = \frac{1}{2} (z_{i} + z_{i + 1})$ and τ_z,i = z_i+1 − z_i, we have

\begin{matrix} \frac{\partial c_{z, i}}{\partial ε} = {\begin{matrix} \frac{1}{2} {\tilde{z}}_{q} & if i = q or i = q - 1, \\ 0 & otherwise, \end{matrix} \\ \frac{\partial τ_{z, i}}{\partial ε} = {\begin{matrix} {\tilde{z}}_{q} & if i = q - 1, \\ - {\tilde{z}}_{q} & if i = q, \\ 0 & otherwise . \end{matrix} \end{matrix}

We consider kernels of the form k_W(x, y) = h(|x − y|²) and we note h_x,y,i,j = h(|c_x,i − c_y,j|²) ∈ ℝ and $h_{x, y, i, j}^{'} = \frac{\partial h ({| c_{x, i} - c_{y, j} |}^{2})}{\partial c_{x, i}} = 2 h' ({| c_{x, i} - c_{y, j} |}^{2}) (c_{x, i} - c_{y, j}) \in ℝ^{d}$ for any sequences of points x, y and indices i, j. We get

\begin{matrix} \frac{\partial E}{\partial ε} = & \sum_{j = 1}^{n - 1} (h_{z, z, q, j}^{'} \cdot {\tilde{z}}_{q}) (τ_{z, q} \cdot τ_{z, j}) \\ + \sum_{j = 1}^{n - 1} (h_{z, z, q - 1, j}^{'} \cdot {\tilde{z}}_{q}) (τ_{z, q - 1} \cdot τ_{z, j}) \\ + 2 \sum_{j = 1}^{n - 1} (h_{z, z, q - 1, j} - h_{z, z, q, j}) ({\tilde{z}}_{q} \cdot τ_{z, j}) \\ - 2 \sum_{j = 1}^{n - 1} (h_{z, y, q - 1, j} - h_{z, y, q, j}) ({\tilde{z}}_{q} \cdot τ_{y, j}) \\ - \sum_{j = 1}^{m - 1} (h_{z, y, q, j}^{'} \cdot {\tilde{z}}_{q}) (τ_{z, q} \cdot τ_{y, j}) \\ - \sum_{j = 1}^{m - 1} (h_{z, y, q - 1, j}^{'} \cdot {\tilde{z}}_{q}) (τ_{z, q - 1} \cdot τ_{y, j}) . \end{matrix}

Hence the gradient of E with respect to z_q is given by

\begin{matrix} \nabla_{z_{q}} E = & \sum_{j = 1}^{n - 1} (τ_{z, q} \cdot τ_{z, j}) h_{z, z, q, j}^{'} \\ + \sum_{j = 1}^{n - 1} (τ_{z, q - 1} \cdot τ_{z, j}) h_{z, z, q - 1, j}^{'} \\ + 2 \sum_{j = 1}^{n - 1} (h_{z, z, q - 1, j} - h_{z, z, q, j}) τ_{z, j} \\ - 2 \sum_{j = 1}^{n - 1} (h_{z, y, q - 1, j} - h_{z, y, q, j}) τ_{y, j} \\ - \sum_{j = 1}^{m - 1} (τ_{z, q} \cdot τ_{y, j}) h_{z, y, q, j}^{'} \\ - \sum_{j = 1}^{m - 1} (τ_{z, q - 1} \cdot τ_{y, j}) h_{z, y, q - 1, j}^{'} . \end{matrix}

(19)

Appendix B: Similarity Transformation

B.1 Quaternion Representation of Similitude Transformation

Here we set d = 3 and look at transformations of the form φ(x) = Rx + b, where R is a similitude matrix defined by the direct product of uniform scale with orthogonal spatial rotation and b is a translation vector. The algebra of quaternions is a useful mathematical tool for formulating the composition of arbitrary spatial rotations, and establishing the correctness of algorithms founded upon such compositions. Here, we use the quaternion q = [a, s] to represent a similitude transformation, where a is a vector with three entries a₁, a₂, a₃ to describe spatial rotation and s is a scalar. We do not restrict the length of q to 1 so that the scaling factor is also considered.

The group (Q, ◦) is defined as the set of quaternions Q with the law of composition ◦: Q × Q → Q, given by

q_{1} ◦ q_{2} = [a_{1} \times a_{2} + s_{1} a_{2} + s_{2} a_{1}, s_{1} s_{2} - a_{1} \cdot a_{2}] .

(20)

The inverse of q is $q^{- 1} = \frac{1}{s^{2} + a \cdot a} q^{*}$ , where q^* is the conjugate of q defined as q^* = [−a, s]. According to the law of composition in (20), the similitude operation R on x ∈ ℝ³ is described as [Rx, 0] = q ◦ [x, 0] ◦ q^*, where

Rx = 2 s a \times x + 2 (a \cdot x) a + (s^{2} - {| a |}^{2}) x .

(21)

B.2 Similarity Alignment of Curves

In the continuous setting, the alignment of two curves C and S is performed through minimization of the following functional:

J (s, a, b) = E (φ (C), S) = {‖ µ_{φ (C)} - µ_{S} ‖}_{W^{*}}^{2},

where φ(x) = Rx + b, with R parametrized by variables s and a via formula (21). When curves C and S are discretized via sequences $x = {(x_{i})}_{i = 1}^{n} and y = {(y_{j})}_{j = 1}^{m}$ , we consider the functional

J (s, a, b) = E (z, y) = {‖ \sum_{i = 1}^{n} τ_{z, i} δ_{c_{z, i}} - \sum_{j = 1}^{m} τ_{y, j} δ_{c_{y, j}} ‖}_{W^{*}}^{2},

where z_i = Rx_i+ b. The derivative of this functional is computed in Appendix C.

Appendix C: Gradient of a Matching Functional with Respect to Parameters of Similarity Transformations

We need to compute the gradient of a dissimilarity functional

J (s, a, b) = E (z, y),

where $z = {(z_{i})}_{i = 1}^{n} = {(φ (x_{i}))}_{i = 1}^{n}$ and φ(x) = Rx+ b, R computed from parameters s and a via formula (21): Rx = 2sa × x + 2(a · x)a + (s² − |a|²)x. Let first compute the gradient of J with respect to parameter s. We have

\begin{matrix} \nabla_{S} J & = \sum_{i = 1}^{n} \frac{\partial φ (x_{i})}{\partial s} \cdot \nabla_{φ (x_{i})} E \\ = \sum_{i = 1}^{n} (2 s x_{i} + 2 a \times x_{i}) \cdot \nabla_{φ (x_{i})} E . \end{matrix}

(22)

The gradient of J with respect to parameters a can be computed as follows. Let a_ε = a + εã and take derivatives at ε = 0. We have

\begin{matrix} \partial_{ε} J & = \sum_{i = 1}^{n} \partial_{ε} (φ (x_{i})) \cdot \nabla_{φ (x_{i})} E \\ = \sum_{i = 1}^{n} - 2 (a \cdot \tilde{a}) (x_{i} \cdot \nabla_{φ (x_{i})} E) + 2 s (\tilde{a} \times x_{i}) \cdot \nabla_{φ (x_{i})} E \\ + 2 (\tilde{a} \cdot x_{i}) (a \cdot \nabla_{φ (x_{i})} E) + 2 (a \cdot x_{i}) (\tilde{a} \cdot \nabla_{φ (x_{i})} E) . \end{matrix}

Since (ã × x_i) · ∇_{φ(x_i)}E = (x_i × ∇_{φ(x_i)}E) · ã, we obtain

\begin{matrix} \partial_{ε} J = \sum_{i = 1}^{n} \tilde{a} \cdot [- 2 (x_{i} \cdot \nabla_{φ (x_{i})} E) a + 2 s (x_{i} \times \nabla_{φ (x_{i})} E) \\ + 2 (a \cdot \nabla_{φ (x_{i})} E) x_{i} + 2 (a \cdot x_{i}) \nabla_{φ (x_{i})} E)] . \end{matrix}

The first and third terms form a double wedge product: −(x_i · ∇_{φ(x_i)}E)a + (a · ∇_{φ(x_i)}E)x_i = (a × x_i) × ∇_{φ(x_i)}E so finally the gradient is

\begin{matrix} \nabla_{a} J = & \sum_{i = 1}^{n} 2 (a \times x_{i}) \times \nabla_{φ (x_{i})} E \\ + 2 s (x_{i} \times \nabla_{φ (x_{i})} E) + 2 (a \cdot x_{i}) \nabla_{φ (x_{i})} E . \end{matrix}

(23)

We can compute the derivative of the gradient of J with respect to translation b in the same way as for s and get

\nabla_{b} J = \sum_{i = 1}^{n} \nabla_{φ (x_{i})} E .

(24)

The gradients with respect to s, a, and b in (22, 23, 24) all involve the term ∇_{φ(x_i)}E given in (19) (with z_i = φ(x_i)).

Appendix D: Gradient of a Point-based Matching Functional in the Large Deformation Setting

We rewrite J into a matrix form

J = γ \int_{0}^{1} α_{t} \cdot k_{V} (x_{t}, x_{t}) α_{t} + E (x_{1}, y),

(25)

where α_t and x_t are vectors of momentum and coordinates of vertices at time t. E denotes the matching functional.

Lemma 2

The gradient of J with respect to momentum α_t with metric given by matrix k_V (x_t, x_t) at time t is of the form (∇J)_t = 2γ α_t + η_t, where vector $η_{t} = \nabla_{x_{1}} E + \int_{t}^{1} {(\partial_{x_{s}} [k_{V} (x_{s}, x_{s}) α_{s}])}^{*} (η_{s} + γ α_{s}) ds$ and ∇_x1E is given in (19).

Proof Our first goal is to compute variation of velocity fields υ_t and trajectories x_t given a variation α^ϵ = α + ϵα̃.

We have

υ_{t} (x) = \sum_{k = 1}^{N} k_{V} (x_{k} (t), x) α_{k} (t) = k_{V} (x_{t}, x) α_{t},

(26)

and

x_{t} = x + \int_{0}^{1} k_{V} (x_{s}, x_{s}) α_{s} ds .

(27)

For a variation α^ϵ = α + ϵα̃, computing the derivative with respect to ϵ in (26) yields the corresponding variation of velocity field υ̃ = ∂_ϵυ^ϵ as the form

{\tilde{υ}}_{t} (x) = \partial_{x_{t}} [k_{V} (x_{t}, x) α_{t}] {\tilde{x}}_{t} + k_{V} (x_{t}, x) {\tilde{α}}_{t},

where ∂_i is the derivative with respect to the ith variable in k_V. Similarly, the corresponding variation of trajectory ${\tilde{x}}_{t} = \partial_{ϵ} φ_{t}^{υ^{ϵ}} (x)$ from (15) is of the form

{\tilde{x}}_{t} = \int_{0}^{t} \partial_{x_{s}} [k_{V} (x_{s}, x_{s}) α_{s}] {\tilde{x}}_{s} + k_{V} (x_{s}, x_{s}) {\tilde{α}}_{s} ds .

To obtain x̃_t a manipulation is needed. The above equation can be rewritten as

\frac{d {\tilde{x}}_{t}}{dt} = \partial_{x_{t}} [k_{V} (x_{t}, x_{t}) α_{t}] {\tilde{x}}_{t} + k_{V} (x_{t}, x_{t}) {\tilde{α}}_{t},

which is a linear differential equation in variable x̃_t. By the variation of constants method, we are able to write the solution of x̃_t as

{\tilde{x}}_{t} = \int_{0}^{t} R_{st} k_{V} (x_{s}, x_{s}) {\tilde{α}}_{s} ds,

where operator R_st gives the solution of the homogeneous equation

\frac{{dR}_{st}}{dt} = \partial_{x_{t}} [k_{V} (x_{t}, x_{t}) α_{t}] R_{st} .

It remains to express the variation of the energy ∂_ϵJ in the form

\begin{matrix} \partial_{ϵ} J = & 2 γ \int_{0}^{1} {\tilde{α}}_{t} \cdot k_{V} (x_{t}, x_{t}) α_{t} dt \\ + γ \int_{0}^{1} α_{t} \cdot \partial_{ϵ} (k_{V} (x_{t}^{ϵ}, x_{t}^{ϵ}) α_{t}) dt + d_{x_{1}} E \partial_{ϵ} (x_{1}^{ϵ}) . \end{matrix}

Substituting υ̃_t (x) and x̃_t in ∂_ϵJ, we have the second term as

\begin{matrix} \int_{0}^{1} α_{t} \cdot \partial_{ϵ} (k_{V} (x_{t}^{ϵ}, x_{t}^{ϵ}) α_{t}) dt \\ = \int_{0}^{1} (\int_{t}^{1} R_{ts}^{*} \partial_{x_{s}} {[k_{V} (x_{s}, x_{s}) α_{s}]}^{*} ds) \cdot k_{V} (x_{t}, x_{t}) {\tilde{α}}_{t} dt . \end{matrix}

The third term can be rewritten as

d_{x_{1}} E \partial_{ϵ} (x_{1}^{ϵ}) = \int_{0}^{1} d_{x_{1}} {ER}_{t 1} k_{V} (x_{t}, x_{t}) {\tilde{α}}_{t} dt .

We finally obtain

\partial_{ϵ} J = \int_{0}^{1} k_{V} (x_{t}, x_{t}) (2 γ α_{t} + η t) \cdot {\tilde{α}}_{t} dt .

The gradient ∇J ∈ L²([0, 1], (ℝ^d)ⁿ) at time t is given

{(\nabla J)}_{t} = k_{V} (x_{t}, x_{t}) (2 γ α_{t} + η_{t}) .

Vector $η_{t} = γ \int_{0}^{1} R_{ts}^{*} \partial_{x_{s}} {[k_{V} (x_{s}, x_{s}) α_{s}]}^{*} ds + R_{t 1}^{*} \nabla_{x_{1}} E$ and it can be written in the backward integral equation

η_{t} = \nabla_{x_{1}} E + \int_{t}^{1} {(\partial_{x_{s}} [k_{V} (x_{s}, x_{s}) α_{s}])}^{*} (η_{s} + γ α_{s}) ds .

(28)

The choice of the metric over momentum α_t in the space of L² is arbitrary. A reasonable choice of metric is given by k_V (x_t, x_t) with two-fold advantages of being closer to the metric inducing the space of velocity field υ and simplifying the formula for the gradient. Therefore, the gradient (∇J)_t can be simplified as

{(\nabla J)}_{t} = 2 γ α_{t} + η_{t} .

Contributor Information

Joan Glaunès, MAP5, CNRS UMR 8145, Université Paris Descartes, 75006 Paris, France.

Anqi Qiu, Division of Bioengineering, National University of Singapore, 7 Engineering Drive 1, Block E3A 04-15, Singapore 117574, Singapore bieqa@nus.edu.sg.

Michael I. Miller, Center for Imaging Science, Johns Hopkins University, Baltimore, MD 21218, USA

Laurent Younes, Department of Applied Mathematics and Statistics, Johns Hopkins University, Baltimore, MD 21218, USA.

References

Allassonnière S, Trouvé A, Younes L. Geodesic shooting and diffeomorphic matching via textured meshes. EMMCVPR. 2005:365–381. [Google Scholar]
Avants B, Gee JC. Geodesic estimation for large deformation anatomical shape and intensity averaging. NeuroImage. 2004;23:139–150. doi: 10.1016/j.neuroimage.2004.07.010. [DOI] [PubMed] [Google Scholar]
Bakircioglu M, Grenander U, Khaneja N, Miller MI. Curve matching on brain surfaces using frenet distances. Human Brain Mapping. 1998;6(5–6):329–333. doi: 10.1002/(SICI)1097-0193(1998)6:5/6<329::AID-HBM1>3.0.CO;2-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bakircioglu M, Joshi S, Miller M. Image processing: Vol. 3661. Proc. SPIE medical imaging 1999. Bellingham: SPIE; 1999. Landmark matching on brain surfaces via large deformation diffeomorphisms on the sphere; pp. 710–715. [Google Scholar]
Beg MF. Variational and computational methods for flows of diffeomorphisms in image matching and growth in computational anatomy. Ph.D. dissertation. Johns Hopkins University; 2003. [Google Scholar]
Beg MF, Miller MI, Trouvé A, Younes L. Computing large deformation metric mappings via geodesic flows of diffeomorphisms. International Journal of Computer Vision. 2005;61(2):139–157. [Google Scholar]
Besl P, McKay N. A method for registration of 3-d shapes. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1992;14(2):239–256. [Google Scholar]
Camion V, Younes L. Geodesic interpolating splines. In: Figueiredo M, Zerubia J, Jain K, editors. Lecture notes in computer sciences: Vol. 2134. EMMCVPR 2001. Berlin: Springer; 2001. [Google Scholar]
Cao Y, Miller M, Winslow R, Younes L. Large deformation diffeomorphic metric mapping of vector fields. IEEE Transactions on Medical Imaging. 2005a;24:1216–1230. doi: 10.1109/tmi.2005.853923. [DOI] [PubMed] [Google Scholar]
Cao Y, Miller MI, Winslow RL, Younes L. ICCV. Los Alamitos: IEEE Comput. Soc.; 2005b. Large deformation diffeomorphic metric mapping of fiber orientations; pp. 1379–1386. [Google Scholar]
Cox MF, Cox MAA. Multidimensional scaling. Boca Raton: Chapman and Hall; 2001. [Google Scholar]
Dupuis P, Grenander U, Miller MI. Variational problems on flows of diffeomorphisms for image matching. Quaterly of Applied Mathematics. 1998;56:587–600. [Google Scholar]
Durrleman S, Pennec X, Trouve A, Ayache N. Measuring brain variability via sulcal lines registration: a diffeomorphic approach. Int. conf. med. image comput. comput. assist. interv. 2007:675–682. doi: 10.1007/978-3-540-75757-3_82. [DOI] [PubMed] [Google Scholar]
Feldmar J, Ayache N. Rigid, affine and locally affine registration of free-form surfaces. International Journal of Computer Vision. 1996;18(2):99–119. [Google Scholar]
Fillard P, Arsigny V, Pennec X, Hayashi K, Thompson P, Ayache N. Measuring brain variability by extrapolating sparse tensor fields measured on sulcal lines. Neuroimage. 2007;34:639–650. doi: 10.1016/j.neuroimage.2006.09.027. [DOI] [PubMed] [Google Scholar]
Gee JC, Bajcsy RK. Elastic matching: Continuum mechanical and probabilistic analysis. In: Toga AW, editor. Brain warping. San Diego: Academic Press; 1999. pp. 183–196. [Google Scholar]
Glaunès J. Transport par difféomorphismes de points, de mesures et de courants pour la comparaison de formes etl l’anatomie numérique. Ph.D. dissertation. Université Paris 13; 2005. [Google Scholar]
Glaunès J, Trouvé A, Younes L. CVPR. Los Alamitos: IEEE Comput. Soc.; 2004. Diffeomorphic matching of distributions: A new approach for unlabelled point-sets and sub-manifolds matching; pp. 712–718. [Google Scholar]
Glaunès J, Trouvé A, Younes L. Modeling planar shape variation via hamiltonian flows of curves. In: Krim H, Yezzi A, editors. Statistics and analysis of shapes. Boston: Birkhauser; 2006. [Google Scholar]
Grenander U, Miller MI. Computational anatomy: An emerging discipline. Quarterly of Applied Mathematics. 1998;56(4):617–694. [Google Scholar]
Han X, Xu C, Prince JL. CVPR’2001 (Kauai, HI) Vol. 2. Los Alamitos: IEEE Comput. Soc.; 2001. A topology preserving deformable model using level set; pp. 765–770. [Google Scholar]
Han X, Xu C, Braga-Neto U, Prince J. Topology correction in brain cortex segmentation using a multiscale, graph-based algorithm. IEEE Transactions on Medical Imaging. 2002;21:109–121. doi: 10.1109/42.993130. [DOI] [PubMed] [Google Scholar]
Helm PA, Younes L, Beg MF, Ennis DB, Leclercq C, Faris OP, McVeigh E, Kass D, Miller MI, Winslow RL. Evidence of structural remodeling in the dyssynchronous failing heart. Circulation Research. 2006;98:125–132. doi: 10.1161/01.RES.0000199396.30688.eb. [DOI] [PubMed] [Google Scholar]
Joshi SC, Miller MI. Landmark matching via large deformation diffeomorphisms. IEEE Transactions on Image Processing. 2000;9(8):1357–1370. doi: 10.1109/83.855431. [DOI] [PubMed] [Google Scholar]
Joshi M, Cui J, Doolittle K, Joshi S, Van Essen D, Wang L, Miller MI. Brain segmentation and the generation of cortical surfaces. NeuroImage. 1999;9:461–476. doi: 10.1006/nimg.1999.0428. [DOI] [PubMed] [Google Scholar]
Joshi SC, Davis B, Jomier M, Gerig G. Unbiased diffeomorphic atlas construction for computational anatomy. NeuroImage. 2004;23:151–160. doi: 10.1016/j.neuroimage.2004.07.068. [DOI] [PubMed] [Google Scholar]
Joshi AA, Shattuck DW, Thompson PM, Leahy RM. Registration of cortical surfaces using sulcal landmarks for group analysis of meg data. International congress series: Vol. 1300. New frontiers in biomagnetism; Proceedings of the 15th international conference on biomagnetism; 21–25 August 2006; Vancouver, BC, Canada. 2007. pp. 229–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
Klassen E, Srivastava A, Mio W, Joshi SH. Analysis of planar shapes using geodesic paths on shape spaces. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2003;26(3):372–383. doi: 10.1109/TPAMI.2004.1262333. [DOI] [PubMed] [Google Scholar]
Leow A, Thompson PM, Protas H, Huang S-C. ISBI. Los Alamitos: IEEE Comput. Soc.; 2004. Brain warping with implicit representations; pp. 603–606. [Google Scholar]
McLachlan RI, Marsland S. N-particle dynamics of the Euler equations for planar diffeomorphisms. Dynamical Systems. 2007;22(3):269–290. [Google Scholar]
Michor PW, Mumford D. An overview of the Riemannian metrics on spaces of curves using the Hamiltonian approach. Applied Computational Harmonic Analysis. 2007;23(1):74–113. [Google Scholar]
Miller MI, Massie AB, Ratnanather JT, Botteron KN, Csernansky JG. Bayesian construction of geometrically based cortical thickness metrics. NeuroImage. 2000;12:676–687. doi: 10.1006/nimg.2000.0666. [DOI] [PubMed] [Google Scholar]
Miller MI, Trouvé A, Younes L. On the metrics and Euler-Lagrange equations of computational anatomy. Annual Review of Biomedical Engineering. 2002;4:375–405. doi: 10.1146/annurev.bioeng.4.092101.125733. [DOI] [PubMed] [Google Scholar]
Mio W, Srivastava A. Elastic-string models for representation and analysis of planar shapes. CVPR. 2004;(2):10–15. [Google Scholar]
Qiu A, Younes L, Wang L, Ratnanather JT, Gillepsie SK, Kaplan G, Csernansky JG, Miller MI. Combining anatomical manifold information via diffeomorphic metric mappings for studying cortical thinning of the cingulate gyrus in schizophrenia. NeuroImage. 2007;37:821–833. doi: 10.1016/j.neuroimage.2007.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ratnanather JT, Barta PE, Honeycutt NA, Lee N, Morris NG, Dziorny AC, Hurdal MK, Pearlson GD, Miller MI. Dynamic programming generation of boundaries of local coordinatized submanifolds in the neocortex: application to the planum temporale. NeuroImage. 2003;20(1):359–377. doi: 10.1016/s1053-8119(03)00238-6. [DOI] [PubMed] [Google Scholar]
Rettmann ME, Han X, Xu C, Prince JL. Automated sulcal segmentation using watersheds on the cortical surface. NeuroImage. 2002;15(2):329–344. doi: 10.1006/nimg.2001.0975. [DOI] [PubMed] [Google Scholar]
Schmidt FR, Clausen M, Cremers D. Shape matching by variational computation of geodesics on a manifold. In: Franke K, Müller K-R, Nickolay B, editors. Lecture notes in computer science: Vol. 4174. DAGM-symposium. Berlin: Springer; 2006. pp. 142–151. [Google Scholar]
Sharon E, Mumford D. 2d-shape analysis using conformal mapping. International Journal of Computer Vision. 2006;70(1):55–75. [Google Scholar]
Thompson P, Toga A. A surface-based technique for warping three-dimensional image of the brain. IEEE Transactions on Medical Imaging. 1996;15(4):402–417. doi: 10.1109/42.511745. [DOI] [PubMed] [Google Scholar]
Thompson PM, Schwartz C, Lin RT, Khan AA, Toga AW. Three–dimensional statistical analysis of sulcal variability in the human brain. Journal of Neuroscience. 1996;16(13):4261–4274. doi: 10.1523/JNEUROSCI.16-13-04261.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
Thompson PM, Hayashi KM, Sowell ER, Gogtay N, Giedd JN, Rapoport JL, de Zubicaray GI, Janke AL, Rose SE, Semple J, Doddrell DM, Wang Y, van Erp TG, Cannon TD, Toga AW. Mapping cortical change in alzheimer’s disease, brain development, and schizophrenia. NeuroImage. 2004;23:S2–S18. doi: 10.1016/j.neuroimage.2004.07.071. [DOI] [PubMed] [Google Scholar]
Trouvé A. An infinite dimensional group approach for physics based models. 1995 (Technical report). Electronically available at http://www.cis.jhu.edu.
Twining C, Marsland S, Taylor C. Measuring geodesic distances on the space of bounded diffeomorphisms; Proceedings of the British machine vision conference (BMVC); September 2002; Cardiff. 2002. pp. 847–856. [Google Scholar]
Vaillant M, Glaunès J. Inform. proc. in med. imaging: Vol. 3565. Lecture notes in comput. sci. Berlin: Springer; 2005. Surface matching via currents; pp. 381–392. [DOI] [PubMed] [Google Scholar]
Welker W. Why does cerebral cortex fissure and fold? Cerebral Cortex. 1990;83:3–136. [Google Scholar]
Yang C, Duraiswami R, Gumerov N, Davis L. Improved fast gauss transform and efficient kernel density estimation. IEEE international conference on computer vision; 2003. pp. 464–471. [Google Scholar]
Younes L. Computable elastic distances between shapes. SIAM Journal on Applied Mathematics. 1998;58:565–586. [Google Scholar]
Zhang Z. Iterative point matching for registration of free-form curves and surfaces. International Journal of Computer Vision. 1994;13(2):119–152. [Google Scholar]

[R1] Allassonnière S, Trouvé A, Younes L. Geodesic shooting and diffeomorphic matching via textured meshes. EMMCVPR. 2005:365–381. [Google Scholar]

[R2] Avants B, Gee JC. Geodesic estimation for large deformation anatomical shape and intensity averaging. NeuroImage. 2004;23:139–150. doi: 10.1016/j.neuroimage.2004.07.010. [DOI] [PubMed] [Google Scholar]

[R3] Bakircioglu M, Grenander U, Khaneja N, Miller MI. Curve matching on brain surfaces using frenet distances. Human Brain Mapping. 1998;6(5–6):329–333. doi: 10.1002/(SICI)1097-0193(1998)6:5/6<329::AID-HBM1>3.0.CO;2-X. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R4] Bakircioglu M, Joshi S, Miller M. Image processing: Vol. 3661. Proc. SPIE medical imaging 1999. Bellingham: SPIE; 1999. Landmark matching on brain surfaces via large deformation diffeomorphisms on the sphere; pp. 710–715. [Google Scholar]

[R5] Beg MF. Variational and computational methods for flows of diffeomorphisms in image matching and growth in computational anatomy. Ph.D. dissertation. Johns Hopkins University; 2003. [Google Scholar]

[R6] Beg MF, Miller MI, Trouvé A, Younes L. Computing large deformation metric mappings via geodesic flows of diffeomorphisms. International Journal of Computer Vision. 2005;61(2):139–157. [Google Scholar]

[R7] Besl P, McKay N. A method for registration of 3-d shapes. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1992;14(2):239–256. [Google Scholar]

[R8] Camion V, Younes L. Geodesic interpolating splines. In: Figueiredo M, Zerubia J, Jain K, editors. Lecture notes in computer sciences: Vol. 2134. EMMCVPR 2001. Berlin: Springer; 2001. [Google Scholar]

[R9] Cao Y, Miller M, Winslow R, Younes L. Large deformation diffeomorphic metric mapping of vector fields. IEEE Transactions on Medical Imaging. 2005a;24:1216–1230. doi: 10.1109/tmi.2005.853923. [DOI] [PubMed] [Google Scholar]

[R10] Cao Y, Miller MI, Winslow RL, Younes L. ICCV. Los Alamitos: IEEE Comput. Soc.; 2005b. Large deformation diffeomorphic metric mapping of fiber orientations; pp. 1379–1386. [Google Scholar]

[R11] Cox MF, Cox MAA. Multidimensional scaling. Boca Raton: Chapman and Hall; 2001. [Google Scholar]

[R12] Dupuis P, Grenander U, Miller MI. Variational problems on flows of diffeomorphisms for image matching. Quaterly of Applied Mathematics. 1998;56:587–600. [Google Scholar]

[R13] Durrleman S, Pennec X, Trouve A, Ayache N. Measuring brain variability via sulcal lines registration: a diffeomorphic approach. Int. conf. med. image comput. comput. assist. interv. 2007:675–682. doi: 10.1007/978-3-540-75757-3_82. [DOI] [PubMed] [Google Scholar]

[R14] Feldmar J, Ayache N. Rigid, affine and locally affine registration of free-form surfaces. International Journal of Computer Vision. 1996;18(2):99–119. [Google Scholar]

[R15] Fillard P, Arsigny V, Pennec X, Hayashi K, Thompson P, Ayache N. Measuring brain variability by extrapolating sparse tensor fields measured on sulcal lines. Neuroimage. 2007;34:639–650. doi: 10.1016/j.neuroimage.2006.09.027. [DOI] [PubMed] [Google Scholar]

[R16] Gee JC, Bajcsy RK. Elastic matching: Continuum mechanical and probabilistic analysis. In: Toga AW, editor. Brain warping. San Diego: Academic Press; 1999. pp. 183–196. [Google Scholar]

[R17] Glaunès J. Transport par difféomorphismes de points, de mesures et de courants pour la comparaison de formes etl l’anatomie numérique. Ph.D. dissertation. Université Paris 13; 2005. [Google Scholar]

[R18] Glaunès J, Trouvé A, Younes L. CVPR. Los Alamitos: IEEE Comput. Soc.; 2004. Diffeomorphic matching of distributions: A new approach for unlabelled point-sets and sub-manifolds matching; pp. 712–718. [Google Scholar]

[R19] Glaunès J, Trouvé A, Younes L. Modeling planar shape variation via hamiltonian flows of curves. In: Krim H, Yezzi A, editors. Statistics and analysis of shapes. Boston: Birkhauser; 2006. [Google Scholar]

[R20] Grenander U, Miller MI. Computational anatomy: An emerging discipline. Quarterly of Applied Mathematics. 1998;56(4):617–694. [Google Scholar]

[R21] Han X, Xu C, Prince JL. CVPR’2001 (Kauai, HI) Vol. 2. Los Alamitos: IEEE Comput. Soc.; 2001. A topology preserving deformable model using level set; pp. 765–770. [Google Scholar]

[R22] Han X, Xu C, Braga-Neto U, Prince J. Topology correction in brain cortex segmentation using a multiscale, graph-based algorithm. IEEE Transactions on Medical Imaging. 2002;21:109–121. doi: 10.1109/42.993130. [DOI] [PubMed] [Google Scholar]

[R23] Helm PA, Younes L, Beg MF, Ennis DB, Leclercq C, Faris OP, McVeigh E, Kass D, Miller MI, Winslow RL. Evidence of structural remodeling in the dyssynchronous failing heart. Circulation Research. 2006;98:125–132. doi: 10.1161/01.RES.0000199396.30688.eb. [DOI] [PubMed] [Google Scholar]

[R24] Joshi SC, Miller MI. Landmark matching via large deformation diffeomorphisms. IEEE Transactions on Image Processing. 2000;9(8):1357–1370. doi: 10.1109/83.855431. [DOI] [PubMed] [Google Scholar]

[R25] Joshi M, Cui J, Doolittle K, Joshi S, Van Essen D, Wang L, Miller MI. Brain segmentation and the generation of cortical surfaces. NeuroImage. 1999;9:461–476. doi: 10.1006/nimg.1999.0428. [DOI] [PubMed] [Google Scholar]

[R26] Joshi SC, Davis B, Jomier M, Gerig G. Unbiased diffeomorphic atlas construction for computational anatomy. NeuroImage. 2004;23:151–160. doi: 10.1016/j.neuroimage.2004.07.068. [DOI] [PubMed] [Google Scholar]

[R27] Joshi AA, Shattuck DW, Thompson PM, Leahy RM. Registration of cortical surfaces using sulcal landmarks for group analysis of meg data. International congress series: Vol. 1300. New frontiers in biomagnetism; Proceedings of the 15th international conference on biomagnetism; 21–25 August 2006; Vancouver, BC, Canada. 2007. pp. 229–232. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R28] Klassen E, Srivastava A, Mio W, Joshi SH. Analysis of planar shapes using geodesic paths on shape spaces. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2003;26(3):372–383. doi: 10.1109/TPAMI.2004.1262333. [DOI] [PubMed] [Google Scholar]

[R29] Leow A, Thompson PM, Protas H, Huang S-C. ISBI. Los Alamitos: IEEE Comput. Soc.; 2004. Brain warping with implicit representations; pp. 603–606. [Google Scholar]

[R30] McLachlan RI, Marsland S. N-particle dynamics of the Euler equations for planar diffeomorphisms. Dynamical Systems. 2007;22(3):269–290. [Google Scholar]

[R31] Michor PW, Mumford D. An overview of the Riemannian metrics on spaces of curves using the Hamiltonian approach. Applied Computational Harmonic Analysis. 2007;23(1):74–113. [Google Scholar]

[R32] Miller MI, Massie AB, Ratnanather JT, Botteron KN, Csernansky JG. Bayesian construction of geometrically based cortical thickness metrics. NeuroImage. 2000;12:676–687. doi: 10.1006/nimg.2000.0666. [DOI] [PubMed] [Google Scholar]

[R33] Miller MI, Trouvé A, Younes L. On the metrics and Euler-Lagrange equations of computational anatomy. Annual Review of Biomedical Engineering. 2002;4:375–405. doi: 10.1146/annurev.bioeng.4.092101.125733. [DOI] [PubMed] [Google Scholar]

[R34] Mio W, Srivastava A. Elastic-string models for representation and analysis of planar shapes. CVPR. 2004;(2):10–15. [Google Scholar]

[R35] Qiu A, Younes L, Wang L, Ratnanather JT, Gillepsie SK, Kaplan G, Csernansky JG, Miller MI. Combining anatomical manifold information via diffeomorphic metric mappings for studying cortical thinning of the cingulate gyrus in schizophrenia. NeuroImage. 2007;37:821–833. doi: 10.1016/j.neuroimage.2007.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R36] Ratnanather JT, Barta PE, Honeycutt NA, Lee N, Morris NG, Dziorny AC, Hurdal MK, Pearlson GD, Miller MI. Dynamic programming generation of boundaries of local coordinatized submanifolds in the neocortex: application to the planum temporale. NeuroImage. 2003;20(1):359–377. doi: 10.1016/s1053-8119(03)00238-6. [DOI] [PubMed] [Google Scholar]

[R37] Rettmann ME, Han X, Xu C, Prince JL. Automated sulcal segmentation using watersheds on the cortical surface. NeuroImage. 2002;15(2):329–344. doi: 10.1006/nimg.2001.0975. [DOI] [PubMed] [Google Scholar]

[R38] Schmidt FR, Clausen M, Cremers D. Shape matching by variational computation of geodesics on a manifold. In: Franke K, Müller K-R, Nickolay B, editors. Lecture notes in computer science: Vol. 4174. DAGM-symposium. Berlin: Springer; 2006. pp. 142–151. [Google Scholar]

[R39] Sharon E, Mumford D. 2d-shape analysis using conformal mapping. International Journal of Computer Vision. 2006;70(1):55–75. [Google Scholar]

[R40] Thompson P, Toga A. A surface-based technique for warping three-dimensional image of the brain. IEEE Transactions on Medical Imaging. 1996;15(4):402–417. doi: 10.1109/42.511745. [DOI] [PubMed] [Google Scholar]

[R41] Thompson PM, Schwartz C, Lin RT, Khan AA, Toga AW. Three–dimensional statistical analysis of sulcal variability in the human brain. Journal of Neuroscience. 1996;16(13):4261–4274. doi: 10.1523/JNEUROSCI.16-13-04261.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R42] Thompson PM, Hayashi KM, Sowell ER, Gogtay N, Giedd JN, Rapoport JL, de Zubicaray GI, Janke AL, Rose SE, Semple J, Doddrell DM, Wang Y, van Erp TG, Cannon TD, Toga AW. Mapping cortical change in alzheimer’s disease, brain development, and schizophrenia. NeuroImage. 2004;23:S2–S18. doi: 10.1016/j.neuroimage.2004.07.071. [DOI] [PubMed] [Google Scholar]

[R43] Trouvé A. An infinite dimensional group approach for physics based models. 1995 (Technical report). Electronically available at http://www.cis.jhu.edu.

[R44] Twining C, Marsland S, Taylor C. Measuring geodesic distances on the space of bounded diffeomorphisms; Proceedings of the British machine vision conference (BMVC); September 2002; Cardiff. 2002. pp. 847–856. [Google Scholar]

[R45] Vaillant M, Glaunès J. Inform. proc. in med. imaging: Vol. 3565. Lecture notes in comput. sci. Berlin: Springer; 2005. Surface matching via currents; pp. 381–392. [DOI] [PubMed] [Google Scholar]

[R46] Welker W. Why does cerebral cortex fissure and fold? Cerebral Cortex. 1990;83:3–136. [Google Scholar]

[R47] Yang C, Duraiswami R, Gumerov N, Davis L. Improved fast gauss transform and efficient kernel density estimation. IEEE international conference on computer vision; 2003. pp. 464–471. [Google Scholar]

[R48] Younes L. Computable elastic distances between shapes. SIAM Journal on Applied Mathematics. 1998;58:565–586. [Google Scholar]

[R49] Zhang Z. Iterative point matching for registration of free-form curves and surfaces. International Journal of Computer Vision. 1994;13(2):119–152. [Google Scholar]

PERMALINK

Large Deformation Diffeomorphic Metric Curve Mapping

Joan Glaunès

Anqi Qiu

Michael I Miller

Laurent Younes

Abstract

1 Introduction

2 Curves as Vector-Valued Measures

2.1 Geometric Curve Representation

Fig. 1.

2.2 Norm on Vector-Valued Measure

Fig. 2.

Proposition 1

2.3 Explicit Expression of the Dual Norm with Kernels

Lemma 1

3 Curve Matching via Deformation Maps

3.1 A General Variational Formulation

3.2 Large Deformation Diffeomorphic Metric Curve Mapping

4 The Discrete Model

4.1 Representation with Vector-Valued Dirac Functionals

4.2 Expression of the Dual Norm

Theorem 1

4.3 Matching Functional, Discrete Case

4.4 LDDMM Variational Formulation in the Discrete Setting

4.5 Algorithm

5 Results

5.1 2D Curve Matching

Examples

Fig. 3.

Fig. 4.

Robustness Against Noise

Fig. 5.

Box Bump Experiment

Fig. 6.

Classification

Fig. 8.

Fig. 9.

5.2 3D Curve Matching

Examples

Fig. 10.

Fig. 11.

Fig. 13.

Fig. 12.

Comparison with Landmark Matching

Fig. 14.

Fig. 15.

Fig. 16.

6 Conclusion

Fig. 7.

Acknowledgements

Appendix A: Gradient of E

Appendix B: Similarity Transformation

B.1 Quaternion Representation of Similitude Transformation

B.2 Similarity Alignment of Curves

Appendix C: Gradient of a Matching Functional with Respect to Parameters of Similarity Transformations

Appendix D: Gradient of a Point-based Matching Functional in the Large Deformation Setting

Lemma 2

Contributor Information

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases