iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://unpaywall.org/10.1007/S11128-023-04182-Z
Further insights on constructing quantum circuits for Camellia block cipher | Quantum Information Processing Skip to main content
Springer Nature Link
Log in

Further insights on constructing quantum circuits for Camellia block cipher

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

The rapid development of quantum technology challenges the security of modern cryptography, which causes concern from the cryptographic community about the quantum implementation of cryptographic algorithms, as it is an important component of many quantum attacks. In this paper, the construction of quantum circuits for Camellia block cipher is investigated. Firstly, a 4-bit S-box is derived from the hardware circuit of the Camellia S-box, which divides the S-box circuit into three parts. Then, based on the rearranged circuit, as well as the implementation of the CCCNOT gate, the construction of the NCT-based circuit for the Camellia S-box is researched. Meanwhile, combined with the observations on the rearranged S-box circuit and the discussion on the in-place implementation of different matrices, a quantum circuit for the Camellia S-box with lower T-depth is presented. As an application, the various S-box circuits are used to construct quantum circuits for the Camellia family. The results reveal that the memory-efficient and depth-efficient quantum circuits of Camellia can be constructed with lower T-depth and \(T\cdot M\) value. Besides, for each instance of Camellia, compared with existing state-of-the-art implementation with lowest T-depth and \(T\cdot M\) value, the depth-efficient circuit designed in this work only costs about 35% of the qubits.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

The datasets generated during and/or analyzed during the current study are available at https://github.com/supporting-mterial-s/q-camellia-s-box.

Notes

  1. Note that the existing memory-efficient and depth-efficient circuits of Camellia in [28] are constructed with Clifford+T gates, which are also adopted in this work as the underlying gate set for a fair comparison.

  2. The source code is available at http://jeremy.jean.free.fr/pub/fse2018_layer_implementations.tar.gz

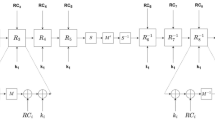
  3. Note that \(y_0,..., y_{17}\) are also the inputs of And gates in the \(H_3\) circuit.

  4. Note that we omit the 32 ancilla qubits for 32 QAND gates in Fig. 10.

References

  1. Grover, L.K.: A fast quantum mechanical algorithm for database search. In: Gary L. Miller, (ed), In: Proceedings of the Twenty-Eighth Annual ACM Symposium on the Theory of Computing, Philadelphia, Pennsylvania, USA, May 22–24, 1996, pp. 212–219. ACM, (1996)

  2. Simon, D.R.: On the power of quantum computation. SIAM J. Comput. 26(5), 1474–1483 (1997)

    Article  MathSciNet  Google Scholar 

  3. Shor, P.W.: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 26(5), 1484–1509 (1997)

    Article  MathSciNet  Google Scholar 

  4. Sheng, Y., Zhou, L., Long, G.: One-step quantum secure direct communication. Sci. Bull. 67(4), 367–374 (2022)

    Article  Google Scholar 

  5. Yin, H., Fu, Y., Li, C., Weng, C., Li, B., Gu, J., Lu, Y., Huang, S., Chen, Z.: Experimental quantum secure network with digital signatures and encryption. Natl. Sci. Rev. 10(4), nwc228 (2023)

    Article  ADS  Google Scholar 

  6. Xie, Y., Lu, Y., Weng, C., Cao, X., Jia, Z., Bao, Y., Wang, Y., Fu, Y., Yin, H., Chen, Z.: Breaking the rate-loss bound of quantum key distribution with asynchronous two-photon interference. PRX Quantum 3(2), 020315 (2022)

    Article  ADS  Google Scholar 

  7. Liu, B., Xia, S., Xiao, D., Huang, W., Xu, B., Li, Y.: Decoy-state method for quantum-key-distribution-based quantum private query. Sci. China Phys. Mech. Astron. 65(4), 240312 (2022)

    Article  ADS  Google Scholar 

  8. Li, C., Fu, Y., Liu, W., Xie, Y., Li, B., Zhou, M., Yin, H., Chen, Z.: Breaking universal limitations on quantum conference key agreement without quantum memory. Commun. Phys. 6, 122 (2023)

    Article  Google Scholar 

  9. Guo, H., Li, Z., Yu, S., Zhang, Y.: Toward practical quantum key distribution using telecom components. Fundam. Res. 1(1), 96–98 (2021)

    Article  Google Scholar 

  10. Shen, A., Cao, X., Wang, Y., Fu, Y., Gu, J., Liu, W., Weng, C., Yin, H., Chen, Z.: Experimental quantum secret sharing based on phase encoding of coherent states. Sci. China Phys. Mech. Astron. 66(6), 260311 (2023)

    Article  ADS  Google Scholar 

  11. Zhang, A., Zhao, S.: Evolutionary-based searching method for quantum circuit architecture. Quantum Inf. Process. 22, 283 (2023)

    Article  ADS  MathSciNet  Google Scholar 

  12. Wu, X., Li, Q., Li, Z., Yang, D., Yang, H., Pan, W., Perkowski, M., Song, X.: Circuit optimization of Grover quantum search algorithm. Quantum Inf. Process. 22, 69 (2023)

    Article  ADS  Google Scholar 

  13. Bonnetain, X., Jaques, S.: Quantum period finding against symmetric primitives in practice. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2022(1), 1–27 (2022)

    Google Scholar 

  14. Daemen, J., Rijmen, V.: The Design of Rijndael: AES - The Advanced Encryption Standard. Springer, Information Security and Cryptography. (2002)

  15. Bertoni, G., Daemen, J., Peeters, M., Van Assche, G.: The Keccak reference. (2011)

  16. NIST: Submission Rrequirements and Evaluation Criteria for the Post-Quantum Cryptography Standardization Process. https://csrc.nist.rip/groups/ST/post-quantum-crypto/documents/call-for-proposals-final-dec-2016.pdf (2016)

  17. Grassl, M., Langenberg, B., Roetteler, M., Steinwandt, R.: Applying grover’s algorithm to AES: quantum resource estimates. In: Takagi,T., (eds.), Post-Quantum Cryptography - 7th International Workshop, PQCrypto 2016, Fukuoka, Japan, Feb 24-26, 2016, Proceedings, vol. 9606 of Lecture Notes in Computer Science, pp. 29–43. Springer, (2016)

  18. Almazrooie, M., Samsudin, A., Abdullah, R., Mutter, K.N.: Quantum reversible circuit of AES-128. Quantum Inf. Process. 17, 112 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  19. Kim, P., Han, D., Jeong, K.C.: Time-space complexity of quantum search algorithms in symmetric cryptanalysis: Applying to AES and SHA-2. Quantum Inf. Process. 17, 339 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  20. Langenberg, B., Pham, H., Steinwandt, R.: Reducing the cost of implementing the advanced encryption standard as a quantum circuit. IEEE Trans. Quantum Eng. 1, 1 (2020)

    Article  Google Scholar 

  21. Jaques, S., Naehrig, M., Roetteler, M., Virdia, F.: Implementing grover oracles for quantum key search on AES and lowmc. In: Canteaut, A., Ishai, Y., (eds.), Advances in Cryptology - EUROCRYPT 2020 - 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, May 10-14, 2020, Proceedings, Part II, vol. 12106 of Lecture Notes in Computer Science, pp. 280-310. Springer, (2020)

  22. Zou, J., Wei, Z., Sun, S., Liu, X., Wu, W.: Quantum circuit implementations of aes with fewer qubits. In: Moriai, S., Wang, H. (eds.), Advances in Cryptology - ASIACRYPT 2020 - 26th International Conference on the Theory and Application of Cryptology and Information Security, Daejeon, South Korea, December 7-11, 2020, Proceedings, Part II, vol. 12492 of Lecture Notes in Computer Science, pp. 697–726. Springer, (2020)

  23. Huang, Z., Sun, S.: Synthesizing quantum circuits of AES with lower t-depth and less qubits. In: Agrawal, S., Lin, D. (eds.), Advances in Cryptology - ASIACRYPT 2022 - 28th International Conference on the Theory and Application of Cryptology and Information Security, Taipei, Taiwan, December 5-9, 2022, Proceedings, Part III, vol. 13793 of Lecture Notes in Computer Science, pp. 614–644. Springer, (2022)

  24. Jang, K., Baksi, A., Song, G., Kim, H., Seo, H., Chattopadhyay, A.: Quantum analysis of AES. IACR Cryptol. ePrint Arch. 2022, 683 (2022)

    Google Scholar 

  25. Li, Z., Cai, B., Sun, H., Liu, H., Wan, L., Qin, S., Wen, Q., Gao, F.: Novel quantum circuit implementation of advanced encryption standard with low costs. Sci. China Phys. Mech. Astron. 65(9), 290311 (2022)

    Article  ADS  Google Scholar 

  26. Wang, Z., Wei, S., Long, G.: A quantum circuit design of AES requiring fewer quantum qubits and gate operations. Front. Phys. 17, 41501 (2022)

    Article  ADS  Google Scholar 

  27. Zou, J., Li, L., Wei, Z., Luo, Y., Liu, Q., Wu, W.: New quantum circuit implementations of SM4 and SM3. Quantum Inf. Process. 21, 181 (2022)

    Article  ADS  MathSciNet  Google Scholar 

  28. Zou, J., Wei, Z., Sun, S., Luo, Y., Liu, Q., Wu, W.: Some efficient quantum circuit implementations of camellia. Quantum Inf. Process. 21, 131 (2022)

    Article  ADS  MathSciNet  Google Scholar 

  29. Li, Z., Gao, F., Qin, S., Wen, Q.: New record in the number of qubits for a quantum implementation of AES. IACR Cryptol. ePrint Arch. 2023, 018 (2023)

    Google Scholar 

  30. Lin, D., Xiang, Z., Xu, R., Zhang, S., Zeng, X.: Optimized quantum implementation of AES. Quantum Inf. Process. 22, 352 (2023)

    Article  ADS  MathSciNet  Google Scholar 

  31. Lin, D., Xiang, Z., Xu, R., Zeng, X., Zhang, S.: Quantum circuit implementations of SM4 block cipher based on different gate sets. Quantum Inf. Process. 22, 282 (2023)

    Article  ADS  MathSciNet  Google Scholar 

  32. Chung, D., Lee, S., Choi, D., Lee. J.: Alternative Tower Field Construction for Quantum Implementation of the AES S-box. IEEE Trans. Comput. 71(10), 2553–2564 (2022)

  33. Shannon, C.E.: Communication theory of secrecy systems. Bell Syst. Tech. J. 28(4), 656–715 (1949)

    Article  MathSciNet  Google Scholar 

  34. Paar, C.: Optimized arithmetic for Reed-Solomon encoders. In: IEEE International Symposium on Information Theory, Ulm, Germany, Jun 29-July 04, 1997, pp. 250. IEEE, (1997)

  35. Boyar, J., Peralta, R.: A new combinational logic minimization technique with applications to cryptology. In: Festa, P. (eds), Experimental Algorithms - SEA 2010 - 9th International Symposium, Ischia Island, Naples, Italy, May 20-22, 2010, Proceedings, vol. 6049 of Lecture Notes in Computer Science, pp. 178–189. Springer, (2010)

  36. Banik, S., Funabiki, Y., Isobe, T.: More results on shortest linear programs. In: Attrapadung, N., Yagi, T. (eds), Advances in Information and Computer Security - IWSEC 2019 - 14th International Workshop on Security, Tokyo, Japan, Aug 28-30, 2019, Proceedings, vol. 11689 of Lecture Notes in Computer Science, pp. 109–128. Springer, (2019)

  37. Tan, Q., Peyrin, T.: Improved heuristics for short linear programs. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2020(1), 203–230 (2020)

    Google Scholar 

  38. Xiang, Z., Zeng, X., Lin, D., Bao, Z., Zhang, S.: Optimizing implementations of linear layers. IACR Trans. Symmetric Cryptol. 2020(2), 120–145 (2020)

    Article  Google Scholar 

  39. Lin, D., Xiang, Z., Zeng, X., Zhang, S.: A framework to optimize implementations of matrices. In: Paterson, K.G. (eds), Topics in Cryptology - CT-RSA 2021 - Cryptographers’ Track at the RSA Conference 2021, Virtual Event, May 17-20, 2021, Proceedings, vol. 12704 of Lecture Notes in Computer Science, pp. 609–632. Springer, (2021)

  40. Jean, J., Peyrin, T., Sim, S.M., Tourteaux, J.: Optimizing implementations of lightweight building blocks. IACR Trans. Symmetric Cryptol. 2017(4), 130–168 (2017)

    Article  Google Scholar 

  41. Bao, Z., Guo, J., Ling, S., Sasaki, Y.: SoK: Peigen - a Platform for evaluation, implementation, and generation of S-boxes. IACR Trans. Symmetric Cryptol. 2019(1), 330–394 (2019)

    Article  Google Scholar 

  42. Bilgin, B., De Meyer, L., Duval, S., Levi, I., Standaert, F.: X: Low and depth and efficient inverses: A guide on S-boxes for low-latency masking. IACR Trans. Symmetric Cryptol. 2020(1), 144–184 (2020)

    Article  Google Scholar 

  43. Dasu, V. A., Baksi, A., SarKar, S., Chattopadhyay, A.: LIGHTER-R: Optimized reversible circuit implementation for SBoxes. In: SOCC 2019 - 32nd IEEE International System-on-Chip Conference, Singapore, 03-06 Sept 2019, pp. 260–265. IEEE, (2019)

  44. Chun, M., Baksi, A., Chattopadhyay, A.: DORCIS: Depth optimized quantum implementation of substitution boxes. IACR Cryptol. ePrint Arch. 2023, 286 (2023)

    Google Scholar 

  45. Li, Z., Gao, F., Qin, S., Wen, Q.: Quantum circuit for implementing Camellia S-box with low costs. Sci. Sin. Phys. Mech. Astron. 53(4), 240313 (2023)

    Article  Google Scholar 

  46. Aoki, K., Ichikawa, T., Kanda,M., Matsui,M., Moriai, S., Nakajima, J., Tokita, T.: Camellia: A 128-bit block cipher suitable for multiple platforms - design and analysis. In: Stinson, D R., Stafford E. Tavares, (eds.), Selected Areas in Cryptography - SAC 2000 - 7th Annual International Workshop, Waterloo, Ontario, Canada, August 14-15, 2000, Proceedings, vol. 2012 of Lecture Notes in Computer Science, pp. 39–56. Springer, (2000)

  47. Standardization administration of the P. R. China: GB/T32907-2016, Information security technology-SM4 Block Cipher Algorithm, (2016)

  48. Amy, M., Maslov, D. Mosca, M., Roetteler, M.: A meet-in-the-middle algorithm for fast synthesis of depth-optimal quantum circuits. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 32(6), 818–830 (2013)

  49. Martínez-Herrera, A.F., Mex-Perera, J.C., Nolazco-Flores, J.A.: Some Representations of the S-Box of Camellia in \(GF(((2^2)^2)^2)\). In: Pieprzyk, J., Sadeghi, AR., Manulis, M. (eds), Cryptology and Network Security, 11th International Conference, CANS 2012, Darmstadt, Germany, Dec 12-14, 2012, Proceedings, vol. 7712 of Lecture Notes in Computer Science, pp. 296–309. Springer, (2012)

  50. Martínez-Herrera, A.F., Mex-Perera, J.C., Nolazco-Flores, J.A.: Merging the Camellia, SMS4 and AES s-boxes in a single s-box with composite bases. In: Desmedt, Y. (eds.), 16th International Conference, ISC 2013, Dallas, Texas, Nov 13-15, 2013, Proceedings, vol. 7807 of Lecture Notes in Computer Science, pp. 209–217. Springer, (2015)

  51. Wei, Z., Sun, S., Hu, L., Wei, M., Boyar, J., Peralta, R.: Scrutinizing the tower field implementation of the \(\mathbb{F} _{2^8}\) inverter-with applications to AES, Camellia, and SM4. IACR Cryptol. ePrint Arch. 2019, 738 (2019)

    Google Scholar 

Download references

Acknowledgements

We would like to thank the anonymous reviewers for their helpful comments and suggestions. This work was supported by the National Natural Science Foundation of China (62272470, 62272147, 61902073) and the Wuhan Science and Technology Bureau (2022010801020328).

Author information

Authors and Affiliations

  1. College of Science, National University of Defense Technology, Changsha, 410073, China

    Da Lin & Bing Sun

  2. State Key Laboratory of Cryptology, P. O. Box 5159, Beijing, 100878, China

    Zejun Xiang

  3. School of Cyber Science and Technology, Hubei University, Wuhan, 430062, China

    Zejun Xiang & Yunyu Guo

  4. College of Computer and Data Science, Fuzhou University, Fuzhou, 350108, China

    Jian Zou

  5. Key Lab of Information Security of Network Systems, Fuzhou University, Fuzhou, 350108, China

    Jian Zou

Authors
  1. Da Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bing Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zejun Xiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jian Zou
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yunyu Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

DL and BS conceived the idea of the study; ZX and JZ refined the idea and analyzed the data; YG interpreted the results; and all authors discussed the results, wrote and revised the manuscript.

Corresponding author

Correspondence to Bing Sun.

Ethics declarations

Conflict of interest

The authors have no competing interests to declare that are relevant to the content of this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

A Quantum-style circuits of \(H_1\) and \(H_3\)

Quantum-style circuit of \(H_1\)

$$\begin{aligned}{} & {} t_{20} = t_{20} \oplus y_{7} \cdot y_{3}, \quad t_{22} = t_{22} \oplus y_{17} \cdot y_{16}, \quad t_{26} = t_{26} \oplus y_{13} \cdot y_{12},\\{} & {} t_{24} = t_{24} \oplus y_{11} \cdot y_{10},\\{} & {} t_{24} = t_{24} \oplus t_{26}, \quad t_{26} = t_{26} \oplus y_{15} \cdot y_{14}, \quad t_{20} = t_{20} \oplus t_{22}, \quad t_{20} = t_{20} \oplus t_{24}, \\{} & {} t_{22} = t_{22} \oplus t_{26}, \quad t_{26} = t_{26} \oplus y_{9} \cdot y_{8}, \quad t_{24} = t_{24} \oplus y_{9} \cdot y_{8}, \quad t_{24} = t_{24} \oplus y_{5} \cdot y_{1}, \\{} & {} t_{26} = t_{26} \oplus y_{4} \cdot y_{0}, \quad t_{22} = t_{22} \oplus y_{6} \cdot y_{2}. \end{aligned}$$

Quantum-style circuit of \(H_3\)

$$\begin{aligned}{} & {} t_{43} = t_{26} \oplus t_{24}, \quad t_{44} = t_{26} \oplus t_{20}, \quad t_{45} = t_{24} \oplus t_{22}, \quad t_{46} = t_{44} \oplus t_{45},\\{} & {} t_{47} = t_{20} \oplus t_{22}, \quad s_{6} = s_{6} \oplus t_{22} \cdot y_{4}, \quad s_{1} = s_{1} \oplus t_{47} \cdot y_{9}, \quad s_{4} = s_{4} \oplus t_{44} \cdot y_{15},\\{} & {} s_{2} = s_{2} \oplus t_{45} \cdot y_{13}, \quad s_{0} = s_{0} \oplus t_{22} \cdot y_{0}, \quad s_{7} = s_{7} \oplus t_{47} \cdot y_{8}, \quad s_{3} = s_{3} \oplus t_{44} \cdot y_{14},\\{} & {} s_{5} = s_{5} \oplus t_{45} \cdot y_{12}, \quad s_{6} = s_{6} \oplus t_{20} \cdot y_{5}, \quad s_{7} = s_{7} \oplus s_{0}, \quad s_{3} = s_{3} \oplus s_{5},\\{} & {} s_{2} = s_{2} \oplus t_{43} \cdot y_{17}, \quad s_{1} = s_{1} \oplus t_{43} \cdot y_{17}, \quad s_{6} = s_{6} \oplus t_{24} \cdot y_{6}, \quad s_{4} = s_{4} \oplus t_{24} \cdot y_{6},\\{} & {} s_{3} = s_{3} \oplus s_{7}, \quad s_{7} = s_{7} \oplus t_{43} \cdot y_{16}, \quad s_{0} = s_{0} \oplus t_{24} \cdot y_{2}, \quad s_{0} = s_{0} \oplus t_{20} \cdot y_{1},\\{} & {} s_{2} = s_{2} \oplus s_{3}, \quad s_{5} = s_{5} \oplus t_{43} \cdot y_{16}, \quad s_{5} = s_{5} \oplus t_{26} \cdot y_{3}, \quad s_{2} = s_{2} \oplus s_{4},\\{} & {} s_{4} = s_{4} \oplus t_{46} \cdot y_{11}, \quad s_{1} = s_{1} \oplus s_{4}, \quad s_{4} = s_{4} \oplus s_{6}, \quad s_{7} = s_{7} \oplus t_{24} \cdot y_{2},\\{} & {} s_{6} = s_{6} \oplus t_{26} \cdot y_{7}, \quad s_{5} = s_{5} \oplus t_{46} \cdot y_{10}, \quad s_{1} = s_{1} \oplus t_{20} \cdot y_{5}, \quad s_{0} = s_{0} \oplus t_{26} \cdot y_{3},\\{} & {} s_{7} = s_{7} \oplus s_{4}, \quad s_{5} = s_{5} \oplus s_{6}, \quad s_{2} = s_{2} \oplus s_{7}, \quad s_{3} = s_{3} \oplus s_{1}, \\{} & {} s_{0} = s_{0} \oplus s_{1}, \quad s_{1} = s_{1} \oplus 1, \quad s_{2} = s_{2} \oplus 1, \quad s_{4} = s_{4} \oplus 1,\\{} & {} s_{5} = s_{5} \oplus 1, \quad s_{6} = s_{6} \oplus 1.\\ \end{aligned}$$

B NCT-based circuit of \(S_1\) with 5 ancilla qubits

Quantum-style circuit of \(H_1\)

$$\begin{aligned}{} & {} t_{20} = t_{20} \oplus y_{7} \cdot y_{3}, \quad t_{22} = t_{22} \oplus y_{17} \cdot y_{16}, \quad t_{26} = t_{26} \oplus y_{13} \cdot y_{12}, \quad t_{24} = t_{24} \oplus y_{11} \cdot y_{10},\\{} & {} t_{24} = t_{24} \oplus t_{26}, \quad t_{26} = t_{26} \oplus y_{15} \cdot y_{14}, \quad t_{20} = t_{20} \oplus t_{22}, \quad t_{20} = t_{20} \oplus t_{24}, \\{} & {} t_{22} = t_{22} \oplus t_{26}, \quad a = a \oplus y_{9} \cdot y_{8}, \quad t_{26} = t_{26} \oplus a, \quad t_{24} = t_{24} \oplus a,\\{} & {} a = a \oplus y_{9} \cdot y_{8}, \quad t_{24} = t_{24} \oplus y_{5} \cdot y_{1}, \quad t_{26} = t_{26} \oplus y_{4} \cdot y_{0}, \quad t_{22} = t_{22} \oplus y_{6} \cdot y_{2}. \end{aligned}$$

NCT-based circuit of \(H_1\)

$$\begin{aligned}{} & {} x_{2} = x_{2} \oplus x_{1} \quad x_{2} = x_{2} \oplus 1 \quad x_{5} = x_{5} \oplus x_{6} \quad x_{5} = x_{5} \oplus x_{1}\\{} & {} x_{5} = x_{5} \oplus x_{0} \quad x_{7} = x_{7} \oplus x_{4} \quad x_{7} = x_{7} \oplus x_{1} \quad x_{7} = x_{7} \oplus x_{0}\\{} & {} x_{3} = x_{3} \oplus x_{5} \quad x_{3} = x_{3} \oplus x_{7} \quad x_{3} = x_{3} \oplus x_{2} \quad x_{6} = x_{6} \oplus x_{5}\\{} & {} x_{6} = x_{6} \oplus x_{4} \quad x_{6} = x_{6} \oplus x_{3} \quad x_{6} = x_{6} \oplus x_{2} \quad x_{6} = x_{6} \oplus x_{1}\\{} & {} x_{6} = x_{6} \oplus 1 \quad x_{0} = x_{0} \oplus x_{5} \quad x_{0} = x_{0} \oplus 1 \quad x_{4} = x_{4} \oplus x_{1}\\{} & {} x_{1} = x_{1} \oplus x_{5} \quad x_{1} = x_{1} \oplus x_{3} \quad x_{1} = x_{1} \oplus x_{6} \quad t_{20} = t_{20} \oplus x_{2} \cdot x_{5}\\{} & {} t_{22} = t_{22} \oplus x_{7} \cdot x_{3} \quad t_{26} = t_{26} \oplus x_{6} \cdot x_{0} \quad t_{24} = t_{24} \oplus x_{4} \cdot x_{1} \quad t_{24} = t_{24} \oplus t_{26}\\{} & {} t_{20} = t_{20} \oplus t_{22} \quad t_{20} = t_{20} \oplus t_{24} \quad x_{6} = x_{6} \oplus x_{4} \quad x_{1} = x_{1} \oplus x_{0}\\{} & {} x_{7} = x_{7} \oplus x_{4} \quad x_{0} = x_{0} \oplus x_{1} \quad x_{0} = x_{0} \oplus x_{3} \quad x_{2} = x_{2} \oplus x_{6}\\{} & {} x_{5} = x_{5} \oplus x_{1} \quad x_{4} = x_{4} \oplus x_{6} \quad x_{4} = x_{4} \oplus x_{7} \quad x_{4} = x_{4} \oplus x_{2}\\{} & {} x_{3} = x_{3} \oplus x_{5} \quad x_{3} = x_{3} \oplus x_{1} \quad t_{26} = t_{26} \oplus x_{6} \cdot x_{1} \quad a = a \oplus x_{7} \cdot x_{0}\\{} & {} t_{24} = t_{24} \oplus x_{2} \cdot x_{5} \quad t_{22} = t_{22} \oplus x_{4} \cdot x_{3} \quad t_{22} = t_{22} \oplus t_{26} \quad t_{24} = t_{24} \oplus a\\{} & {} t_{26} = t_{26} \oplus a \quad x_{2} = x_{2} \oplus x_{7} \quad x_{5} = x_{5} \oplus x_{0} \quad a = a \oplus x_{7} \cdot x_{0}\\{} & {} t_{26} = t_{26} \oplus x_{2} \cdot x_{5} \quad x_{4} = x_{4} \oplus x_{5} \quad x_{4} = x_{4} \oplus x_{7} \quad x_{4} = x_{4} \oplus x_{3}\\{} & {} x_{4} = x_{4} \oplus x_{2} \quad x_{4} = x_{4} \oplus x_{0} \quad t_{20} = t_{20} \oplus x_{4} \quad x_{6} = x_{6} \oplus x_{5}\\{} & {} x_{6} = x_{6} \oplus x_{2} \quad x_{6} = x_{6} \oplus x_{1} \quad t_{22} = t_{22} \oplus x_{6} \quad x_{4} = x_{4} \oplus x_{5}\\{} & {} x_{4} = x_{4} \oplus x_{7} \quad x_{4} = x_{4} \oplus x_{2} \quad x_{4} = x_{4} \oplus x_{0} \quad t_{24} = t_{24} \oplus x_{4}\\{} & {} x_{6} = x_{6} \oplus x_{7} \quad x_{6} = x_{6} \oplus x_{0} \quad t_{26} = t_{26} \oplus x_{6}.\\ \end{aligned}$$

NCT-based circuit of \(H_2\)

$$\begin{aligned}{} & {} t_{22} = t_{22} \oplus 1, \quad a = a \oplus t_{26} \cdot t_{22}, \quad t_{24} = t_{24}\oplus a \cdot t_{20}, \quad t_{26} = t_{26} \oplus t_{24},\\{} & {} t_{22} = t_{22} \oplus 1, \quad t_{22} = t_{22} \oplus t_{20} \cdot t_{24}, \quad t_{24} = t_{24} \oplus t_{22} \cdot t_{26}, \quad t_{20} = t_{20} \oplus t_{22},\\{} & {} t_{22} = t_{22} \oplus t_{20} \cdot t_{24}, \quad t_{24} = t_{24} \oplus t_{26}, \quad t_{26} = t_{26} \oplus t_{22} \cdot t_{24}.\\ \end{aligned}$$

Quantum-style circuit of \(H_3\) The quantum-style circuit of \(H_3\) is the same as the one designed for the case that 4 ancilla qubits are allocated, since the \(H_3\) circuit consumes no additional ancilla qubits except \(t_{20}, t_{22}, t_{24}\) and \(t_{26}\) NCT-based circuit of \(H_3\)

$$\begin{aligned}{} & {} t_{20} = t_{20} \oplus t_{22}, \quad t_{26} = t_{26} \oplus t_{24}, \quad x_{1} = x_{1} \oplus x_{5}, \quad x_{1} = x_{1} \oplus x_{4},\\{} & {} x_{1} = x_{1} \oplus x_{3}, \quad x_{1} = x_{1} \oplus x_{6}, \quad x_{1} = x_{1} \oplus x_{0}, \quad x_{4} = x_{4} \oplus x_{3},\\{} & {} s_{6} = s_{6} \oplus t_{22}\cdot x_{2}, \quad s_{7} = s_{7} \oplus t_{20}\cdot x_{0}, \quad s_{1} = s_{1} \oplus t_{26}\cdot x_{1}, \quad s_{4} = s_{4} \oplus t_{24}\cdot x_{4},\\{} & {} t_{20} = t_{20} \oplus t_{22}, \quad t_{24} = t_{24} \oplus t_{22}, \quad x_{7} = x_{7} \oplus x_{2}, \quad x_{3} = x_{3} \oplus x_{5},\\{} & {} s_{6} = s_{6} \oplus t_{20}\cdot x_{7}, \quad s_{0} = s_{0} \oplus t_{22}\cdot x_{5}, \quad s_{2} = s_{2} \oplus t_{26}\cdot x_{1}, \quad s_{5} = s_{5} \oplus t_{24}\cdot x_{3},\\{} & {} s_{7} = s_{7} \oplus s_{0}, \quad s_{3} = s_{3} \oplus s_{5}, \quad t_{22} = t_{22} \oplus t_{24}, \quad t_{26} = t_{26} \oplus t_{22},\\{} & {} t_{20} = t_{20} \oplus t_{24}, \quad t_{20} = t_{20} \oplus t_{26}, \quad t_{24} = t_{24} \oplus t_{20}, \quad x_{1} = x_{1} \oplus x_{4},\\{} & {} x_{1} = x_{1} \oplus x_{6}, \quad x_{0} = x_{0} \oplus x_{3}, \quad x_{0} = x_{0} \oplus x_{1}, \quad x_{0} = x_{0} \oplus x_{5},\\{} & {} x_{6} = x_{6} \oplus x_{7}, \quad x_{6} = x_{6} \oplus x_{1}, \quad s_{6} = s_{6} \oplus t_{22}\cdot x_{4}, \quad s_{0} = s_{0} \oplus t_{26}\cdot x_{1},\\{} & {} s_{5} = s_{5} \oplus t_{20}\cdot x_{0}, \quad s_{4} = s_{4} \oplus t_{24}\cdot x_{6}, \quad s_{3} = s_{3} \oplus s_{7}, \quad t_{26} = t_{26} \oplus t_{22},\\{} & {} t_{20} = t_{20} \oplus t_{24}, \quad x_{5} = x_{5} \oplus x_{3}, \quad x_{1} = x_{1} \oplus x_{5}, \quad x_{4} = x_{4} \oplus x_{2},\\{} & {} x_{0} = x_{0} \oplus x_{3}, \quad s_{0} = s_{0} \oplus t_{22}\cdot x_{5}, \quad s_{7} = s_{7} \oplus t_{26}\cdot x_{1}, \quad s_{2} = s_{2} \oplus t_{20}\cdot x_{4},\\{} & {} s_{3} = s_{3} \oplus t_{24}\cdot x_{0}, \quad s_{2} = s_{2} \oplus s_{3}, \quad s_{2} = s_{2} \oplus s_{4}, \quad t_{20} = t_{20} \oplus t_{24},\\{} & {} t_{26} = t_{26} \oplus t_{22}, \quad t_{24} = t_{24} \oplus t_{26}, \quad x_{6} = x_{6} \oplus x_{4}, \quad x_{1} = x_{1} \oplus x_{5},\\{} & {} s_{4} = s_{4} \oplus t_{20}\cdot x_{6}, \quad s_{7} = s_{7} \oplus t_{22}\cdot x_{5}, \quad s_{5} = s_{5} \oplus t_{26}\cdot x_{1}, \quad s_{1} = s_{1} \oplus t_{24}\cdot x_{7}, \\{} & {} s_{1} = s_{1} \oplus s_{4}, \quad s_{4} = s_{4} \oplus s_{6}, \quad t_{22} = t_{26} \oplus t_{22}, \quad t_{20} = t_{22} \oplus t_{20},\\{} & {} x_{4} = x_{4} \oplus x_{6}, \quad x_{4} = x_{4} \oplus x_{7}, \quad x_{0} = x_{0} \oplus x_{1}, \quad x_{5} = x_{5} \oplus x_{1},\\{} & {} x_{2} = x_{2} \oplus x_{7}, \quad s_{6} = s_{6} \oplus t_{26}\cdot x_{4}, \quad s_{0} = s_{0} \oplus t_{24}\cdot x_{0}, \quad s_{5} = s_{5} \oplus t_{22}\cdot x_{5},\\{} & {} s_{1} = s_{1} \oplus t_{20}\cdot x_{2}, \quad s_{7} = s_{7} \oplus s_{4}, \quad s_{5} = s_{5} \oplus s_{6}, \quad s_{2} = s_{2} \oplus s_{7}, \\{} & {} s_{3} = s_{3} \oplus s_{1}, \quad s_{0} = s_{0} \oplus s_{1}, \quad s_{1} = s_{1} \oplus 1, \quad s_{2} = s_{2} \oplus 1,\\{} & {} s_{4} = s_{4} \oplus 1, \quad s_{5} = s_{5} \oplus 1, \quad s_{6} = s_{6} \oplus 1. \end{aligned}$$

C Matrices derived from inputs of AND gates

Matrix derived from the \(H_1/H_3\) circuit

$$\begin{aligned} \begin{bmatrix} 1&{} 1&{} 1&{} 1&{} 1&{} 1&{} 1&{} 1\\ 1&{} 1&{} 1&{} 0&{} 1&{} 0&{} 1&{} 0\\ 1&{} 0&{} 1&{} 1&{} 1&{} 0&{} 0&{} 1\\ 1&{} 1&{} 0&{} 0&{} 0&{} 1&{} 1&{} 0\\ 0&{} 0&{} 1&{} 1&{} 1&{} 0&{} 1&{} 0\\ 1&{} 0&{} 1&{} 1&{} 1&{} 0&{} 1&{} 1\\ 1&{} 0&{} 1&{} 0&{} 1&{} 0&{} 0&{} 1\\ 0&{} 1&{} 1&{} 0&{} 0&{} 0&{} 0&{} 0\\ 0&{} 0&{} 0&{} 1&{} 0&{} 1&{} 0&{} 1\\ 1&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 1\\ 0&{} 1&{} 1&{} 0&{} 1&{} 0&{} 1&{} 0\\ 0&{} 1&{} 0&{} 0&{} 1&{} 0&{} 0&{} 0\\ 0&{} 1&{} 0&{} 0&{} 0&{} 1&{} 1&{} 0\\ 1&{} 0&{} 0&{} 1&{} 0&{} 0&{} 1&{} 1\\ 0&{} 0&{} 1&{} 0&{} 1&{} 1&{} 0&{} 0\\ 1&{} 1&{} 0&{} 1&{} 1&{} 0&{} 1&{} 1\\ 0&{} 1&{} 1&{} 1&{} 1&{} 1&{} 1&{} 1\\ 1&{} 1&{} 0&{} 0&{} 1&{} 0&{} 0&{} 1 \end{bmatrix} \end{aligned}$$

Matrices derived from the \(H_2\) circuit

$$\begin{aligned} M_1 = \begin{bmatrix} 0&{}1&{}1&{}1\\ 1&{}0&{}1&{}1\\ 0&{}1&{}0&{}1\\ 1&{}1&{}1&{}0\\ 1&{}0&{}1&{}0\\ 1&{}1&{}0&{}1 \end{bmatrix}, M_2 = \begin{bmatrix} 1&{}0&{}0&{}1&{}0&{}1&{}1\\ 1&{}0&{}1&{}0&{}1&{}0&{}0\\ 1&{}1&{}1&{}1&{}1&{}1&{}0\\ 1&{}0&{}0&{}0&{}1&{}1&{}0\\ 1&{}0&{}0&{}1&{}0&{}1&{}0\\ 0&{}1&{}0&{}0&{}0&{}0&{}0\\ 1&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}1&{}1&{}0&{}0&{}1 \end{bmatrix}. \end{aligned}$$

D In-place implementation of the P-function

Denote by \((x_0,...,x_7)\) and \((y_0,...,y_7)\) the 64-bit input and output of the P-function. The calculation of \((y_0,...,y_7)\) under S-Xor metric can be completed as follows.

$$\begin{aligned} \begin{array}{llll} x_{0} = x_{0} \oplus x_{6}, &{}x_{1} = x_{1} \oplus x_{7}, &{}x_{2} = x_{2} \oplus x_{4}, &{}x_{4} = x_{4} \oplus x_{0},\\ x_{6} = x_{6} \oplus x_{1}, &{}x_{0} = x_{0} \oplus x_{5}, &{}x_{3} = x_{3} \oplus x_{4}, &{}x_{5} = x_{5} \oplus x_{3} ~(y_{7}),\\ x_{3} = x_{3} \oplus x_{1} ~(y_{1}), &{}x_{7} = x_{7} \oplus x_{2}, &{}x_{1} = x_{1} \oplus x_{0} ~(y_{4}), &{}x_{7} = x_{7} \oplus x_{5} ~(y_{0}),\\ x_{2} = x_{2} \oplus x_{6} ~(y_{5}), &{}x_{4} = x_{4} \oplus x_{7} ~(y_{6}), &{}x_{6} = x_{6} \oplus x_{4} ~(y_{3}), &{}x_{0} = x_{0} \oplus x_{2} ~(y_{2}). \end{array} \end{aligned}$$

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lin, D., Sun, B., Xiang, Z. et al. Further insights on constructing quantum circuits for Camellia block cipher. Quantum Inf Process 22, 455 (2023). https://doi.org/10.1007/s11128-023-04182-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-023-04182-z

Keywords

Search

Navigation