iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://unpaywall.org/10.1007/S11075-022-01442-4
A modified local and parallel finite element method for the coupled Stokes-Darcy model with the Beavers-Joseph interface condition | Numerical Algorithms Skip to main content
Springer Nature Link
Log in

A modified local and parallel finite element method for the coupled Stokes-Darcy model with the Beavers-Joseph interface condition

  • Original Research
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

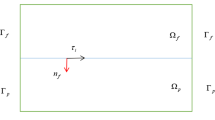
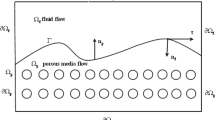
In this paper, by combining a partition of unity with backtracking technique, a modified local and parallel finite element method (MLPFEM) is proposed and investigated for the coupled Stokes-Darcy problem with the Beavers-Joseph (BJ) interface condition. The well-posedness of the coupled Stokes-Darcy model with BJ interface condition is established when the parameter αBJ is small enough in Cao et al. (Commun. Math. Sci. 8(1), 1–25 2010). The MLPFEM is adopted based on its significant advantages that we only need to solve a series of local subproblems once the coarse approximation is derived. Compared with the global discontinuous solution by the algorithm in Du and Zuo (2017), the main features of our algorithm are as follows: (1) partition of unity functions are utilized to gather local approximations computed on a fine grid by local and parallel procedures to generate a global continuous solution; (2) a further global coarse correction, namely the backtracking technique, is considered to obtain optimal error bounds of the velocity field and the piezometric head in L2 norm. Optimal error bounds are derived and numerical tests are carried out to support the theoretical analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Cao, Y., Gunzburger, M., He, X., Wang, X.: Robin-Robin domain decomposition methods for the steady-state Stokes-Darcy system with the Beavers-Joseph interface condition. Numer. Math. 117(4), 601–629 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  2. Cao, Y., Gunzburger, M., He, X., Wang, X.: Parallel, non-iterative, multi-physics domain decomposition methods for time-dependent Stokes-Darcy systems. Math. Comput. 83(288), 1617–1644 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  3. Cao, Y., Gunzburger, M., Hua, F., Wang, X.: Coupled Stokes-Darcy model with Beavers-Joseph interface boundary condition. Commun. Math. Sci. 8(1), 1–25 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  4. Chen, W., Gunzburger, M., Hua, F., Wang, X.: A parallel Robin-Robin domain decomposition method for the Stokes-Darcy system. SIAM J. Numer. Anal. 49(3), 1064–1084 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  5. Discacciati, M., Quarteroni, A., Valli, A.: Robin-Robin domain decomposition methods for the Stokes-Darcy coupling. SIAM J. Numer. Anal. 45(3), 1246–1268 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  6. Du, G., Zuo, L.: A two-grid method with backtracking for the mixed Stokes/Darcy model. J. Numer. Math. 29(1), 39–46 (2021)

    MathSciNet  MATH  Google Scholar 

  7. Du, G., Li, Q., Zhang, Y.: A two-grid method with backtracking for the mixed Navier-Stokes/Darcy model. Numer. Methods Partial Diff. Equa. 36(6), 1601–1610 (2020)

    Article  MathSciNet  Google Scholar 

  8. Du, G., Zuo, L.: A parallel partition of unity scheme based on two-grid discretizations for the Navier-Stokes problem. J. Sci. Comput. 75(3), 1445–1462 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  9. Du, G., Zuo, L.: A parallel iterative finite element method for the linear elliptic equations. J. Sci. Comput. 85(2), 35 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  10. Du, G., Zuo, L., Zhang, Y.: A new local and parallel finite element method for the coupled Stokes-Darcy model. J. Sci. Comput. 90(1), 43 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  11. Du, G., Zuo, L.: Local and parallel finite element method for the mixed Navier-Stokes/Darcy model with Beavers-Joseph interface conditions. Acta Math. Sci. 37(5), 1331–1347 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  12. Du, G., Zuo, L.: Local and parallel finite element methods for the coupled Stokes/Darcy model. Numer. Algor., 1593-1611 (2021)

  13. Du, G.: Expandable parallel finite element methods for linear elliptic problems. Acta Math. Sci. 40B(2), 572–588 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  14. Du, G., Zuo, L.: Local and parallel finite element post-processing scheme for the Stokes problem. Comput. Math. Applic., 129–140 (2017)

  15. He, Y., Xu, J., Zhou, A.: Local and parallel finite element algorithms for the Navier-Stokes problem. J. Comput. Math., 227–238 (2006)

  16. He, Y., Xu, J., Zhou, A., Li, J.: Local and parallel finite element algorithms for the Stokes problem. Numer. Math. 109(3), 415–434 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  17. Hou, Y.: Optimal error estimates of a decoupled scheme based on two-grid finite element for mixed Stokes-Darcy model. Appl. Math. Lett. 57, 90–96 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  18. Jiang, B.: A parallel domain decomposition method for coupling of surface and groundwater flows. Comput. Methods Appl. Mech. Eng. 198(9-12), 947–957 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  19. Li, Q., Du, G.: Local and parallel finite element methods based on two-grid discretizations for the nonstationary Navier-Stokes equations. Numer. Algor. 88(4), 1915–1936 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  20. Li, Q., Du, G.: Local and parallel finite element methods based on two-grid discretizations for unsteady convection-diffusion problem. Numer. Methods Partial Diff. Equa. 37(6), 3023–3041 (2021)

    Article  MathSciNet  Google Scholar 

  21. Li, R., Gao, Y., Li, J., Chen, Z.: A weak galerkin finite element method for a coupled Stokes-Darcy problem on general meshes. J. Comput. Appl. Math. 334, 111–127 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  22. Li, Y., Hou, Y., Layton, W., Zhao, H.: Adaptive partitioned method for the time-accurate approximation of the evolutionary Stokes-Darcy system. Comput. Methods Appl. Mech. Eng. 364, 112923 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  23. Mu, M., Xu, J.: A two-grid method of a mixed Stokes-Darcy model for coupling fluid flow with porous media flow. SIAM J. Numer. Anal. 45 (5), 1801–1813 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  24. Qin, Y., Hou, Y., Huang, P., Wang, Y.: Numerical analysis of two grad-div stabilization methods for the time-dependent Stokes/Darcy model. Comput. Math. Applic. 73(9), 817–832 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  25. Shan, L., Zheng, H.: Partitioned time stepping method for fully evolutionary Stokes-Darcy flow with Beavers-Joseph interface conditions. SIAM J. Numer. Anal. 51(2), 813–839 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  26. Shang, Y., Wang, K.: Local and parallel finite element algorithms based on two-grid discretizations for the transient Stokes equations. Numer. Algor. 54(2), 195–218 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  27. Shang, Y., He, Y.: Parallel iterative finite element algorithms based on full domain partition for the stationary Navier-Stokes equations. Appl. Numer. Math. 60(7), 719–737 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  28. Shang, Y., He, Y., Kim, D., Zhou, X.: A new parallel finite element algorithm for the stationary Navier-Stokes equations. Finite Elem. Anal. Des. 47(11), 1262–1279 (2011)

    Article  MathSciNet  Google Scholar 

  29. Song, L., Li, P., Gu, Y., Fan, C.: Generalized finite difference method for solving stationary 2D and 3D stokes equations with a mixed boundary condition. Comput. Math. Applic. 80(6), 1726–1743 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  30. Sun, Y., Sun, W., Zheng, H.: Domain decomposition method for the fully-mixed Stokes-Darcy coupled problem. Comput. Methods Appl. Mech. Eng. 374, 113578 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  31. Vassilev, D., Wang, C., Yotov, I.: Domain decomposition for coupled Stokes and Darcy flows. Comput. Methods Appl. Mech. Eng. 268, 264–283 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  32. Wang, X., Du, G., Zuo, L.: A novel local and parallel finite element method for the mixed Navier-Stokes-Darcy problem. Comput. Math. Applic. 90 (15), 73–79 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  33. Xu, J., Zhou, A.: Local and parallel finite element algorithms based on two-grid discretizations. Math. Comput. 69(231), 881–909 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  34. Yu, J., Shi, F., Zheng, H.: Local and parallel finite element algorithms based on the partition of unity for the Stokes problem. SIAM J. Sci. Comput. 36(5), C547–C567 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  35. Yu, J., Sun, Y., Shi, F., Zheng, H.: Nitsches type stabilized finite element method for the fully mixed Stokes-Darcy problem with Beavers-Joseph conditions. Appl. Math. Lett. 110, 106588 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  36. Zheng, H., Yu, J., Shi, F.: Local and parallel finite element method based on the partition of unity for incompressible flow. J. Sci. Comput. 65(2), 512–532 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  37. Zheng, H., Song, L., Hou, Y., Zhang, Y.: The partition of unity parallel finite element algorithm. Adv. Comput. Math. 41(4), 937–951 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  38. Zuo, L., Du, G.: A parallel two-grid linearized method for the coupled Navier-Stokes-Darcy problem. Numer. Algor. 77(1), 151–165 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  39. Zuo, L., Du, G.: A multi-grid technique for coupling fluid flow with porous media flow. Comput. Math. Applic. 75(11), 4012–4021 (2018)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

This work is subsidized by the National Natural Science Foundation of China (Nos. 12172202, 11701343, 12101494), the Natural Science Foundation of Shandong Province (Grant No. ZR2021MA063), the Natural Science Foundation of Shaanxi Province (2021JQ-426), and the Scientific Research Program of Shaanxi Provincial Education Department (21JK0935).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Shandong Normal University, Jinan, 250014, China

    Xinhui Wang & Guangzhi Du

  2. School of Mathematics, Northwest University, Xi’an, Shaanxi, 710127, China

    Yi Li

Authors
  1. Xinhui Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guangzhi Du
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yi Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Guangzhi Du.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Data availability

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, X., Du, G. & Li, Y. A modified local and parallel finite element method for the coupled Stokes-Darcy model with the Beavers-Joseph interface condition. Numer Algor 93, 815–831 (2023). https://doi.org/10.1007/s11075-022-01442-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-022-01442-4

Keywords

Search

Navigation