iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://unpaywall.org/10.1007/S11075-010-9369-X
Dimension elevation for Chebyshevian splines | Numerical Algorithms Skip to main content
Springer Nature Link
Log in

Dimension elevation for Chebyshevian splines

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

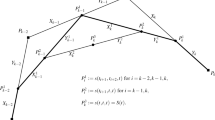
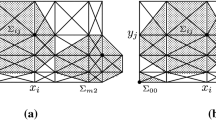
Dimension elevation refers to the Chebyshevian version of the classical degree elevation process for polynomials or polynomial splines. In this paper, we consider the case of splines. The original spline space is based on a given Extended Chebsyhev space \({\mathbb{E}}\) contained in another Extended Chebsyhev space \({\mathbb{E}}^*\) of dimension increased by one. The original spline space, based on \({\mathbb{E}}\), is then embedded in a larger one, based on \(\mathbb{E}^*\). Thanks to blossoms we show how to compute the new poles of any spline in the original spline space in terms of its initial poles.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Cohen, E., Lyche, T., Schumaker, L.L.: Algorithms for degree raising of splines. ACM Trans. Graph. 4, 171–181 (1985)

    Article  MATH  Google Scholar 

  2. Cohen, E., Lyche, T., Schumaker, L.L.: Degree raising for splines. J. Approx. Theory 46, 170–181 (1986)

    Article  MATH  MathSciNet  Google Scholar 

  3. Liu, W.: A simple, efficient degree raising algorithm for B-spline curves. Comput. Aided Geom. Des. 14, 693–698 (1997)

    Article  MATH  Google Scholar 

  4. Lyche, T.: A recurrence relation for Chebyshevian B-splines. Constr. Approx. 1, 155–178 (1985)

    Article  MATH  MathSciNet  Google Scholar 

  5. Mazure, M.-L.: Chebyshev spaces with polynomial blossoms. Adv. Comput. Math. 10, 219–238 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  6. Mazure, M.-L.: Blossoming: a geometrical approach. Constr. Approx. 15, 33–68 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  7. Mazure, M.-L.: Understanding recurrence relations for Chebyshevian B-splines via blossoms. J. Comput. Appl. Math. 219, 457–470 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  8. Mazure, M.-L.: Dimension elevation formula for Chebyshevian blossoms. Comput. Aided. Des. 26, 1016–1027 (2009)

    MathSciNet  Google Scholar 

  9. Mazure, M.-L., Laurent, P.-J.: Polynomial Chebyshev splines. Comput. Aided Geom. Des. 16, 317–343 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  10. Pottmann, H.: The geometry of Tchebycheffian splines. Comput. Aided Geom. Des. 10, 181–210 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  11. Prautzsch, H.: Degree elevation of B-spline curves. Comput. Aided Geom. Des. 18, 193–198 (1984)

    Article  Google Scholar 

  12. Prautzsch, H., Piper, B.: A fast algorithm to raise the degree of B-spline curves. Comput. Aided Geom. Des. 8, 253–266 (1991)

    Article  MATH  MathSciNet  Google Scholar 

  13. Ramshaw, L.: Blossoms are polar forms. Comput. Aided Geom. Des. 6, 323–358 (1989)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratoire Jean Kuntzmann, Université Joseph Fourier, BP53, 38041, Grenoble Cedex 9, France

    Marie-Laurence Mazure

Authors
  1. Marie-Laurence Mazure
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Marie-Laurence Mazure.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mazure, ML. Dimension elevation for Chebyshevian splines. Numer Algor 56, 1–16 (2011). https://doi.org/10.1007/s11075-010-9369-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-010-9369-x

Keywords

AMS Subject Classification

Search

Navigation