iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://unpaywall.org/10.1007/S11063-023-11153-Z
Quasi-Projective and Mittag-Leffler Synchronization of Discrete-Time Fractional-Order Complex-Valued Fuzzy Neural Networks | Neural Processing Letters Skip to main content

Advertisement

Springer Nature Link
Log in

Quasi-Projective and Mittag-Leffler Synchronization of Discrete-Time Fractional-Order Complex-Valued Fuzzy Neural Networks

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

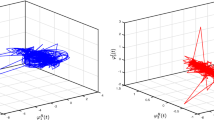
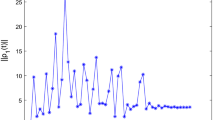
In this paper, we consider a type of discrete-time fractional-order complex-valued fuzzy neural networks. First, based on symbolic functions and complex-valued theory, two new inequalities are established to study synchronization problems of networks. Secondly, two simple and original control strategies including linear feedback controller and adaptive controller which can better reduce the control cost, are designed to guarantee quasi-projective synchronization and Mittag-Leffler synchronization of the considered networks, then sufficient synchronization criteria with simplified algebraic conditions are established on the basis of our established lemmas and some inequality techniques. Finally, numerical simulations are given to check effectiveness of the proposed results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Hoppensteadt F, Izhikevich E (2000) Pattern recognition via synchronization in phase-locked loop neural networks. IEEE Trans Neural Netw 11:734–738

    Article  Google Scholar 

  2. Oong H, Isa N (2011) Adaptive evolutionary artificial neural networks for pattern classification. IEEE Trans Neural Netw 22:1823–1836

    Article  Google Scholar 

  3. Li B, Chow M, Tipsuwan Y, Hung J (2000) Neural-network-based motor rolling bearing fault diagnosis. IEEE Trans Ind Electron 47:1060–1069

    Article  Google Scholar 

  4. Zun̄iga Aguilar C, Gómez-Aguilar J, Alvarado-Martlnez V, Romero-Ugalde H, (2020) Fractional order neural networks for system identification. Chaos Solitons Fract 130:109444

  5. Shen H, Zhu Y, Zhang L, Park J (2017) Extended dissipative state estimation for Markov jump neural networks with unreliable links. IEEE Trans Neural Netw Learn Syst 28:346–358

    Article  MathSciNet  Google Scholar 

  6. Wu G, Abdeljawad T, Liu J, Baleanu D, Wu K (2019) Mittag-Leffler stability analysis of fractional discrete-time neural networks via fixed point technique. Nonlinear Anal Model Control 24:919–936

    MathSciNet  MATH  Google Scholar 

  7. Singh S, Kumar U, Das S, Alsaadi F, Cao J (2022) Synchronization of quaternion valued neural networks with mixed time delays using Lyapunov function method. Neural Process Lett 54:785–801

    Article  Google Scholar 

  8. Atıcı F, Eloe P (2012) Gronwall’s inequality on discrete fractional calculus. Comput Math Appl 64:3193–3200

    MathSciNet  MATH  Google Scholar 

  9. Goodrich C (2015) Peterson A (2015) Discrete Fractional Calculus. Springer, New York

    Book  Google Scholar 

  10. Bao H, Park J, Cao J (2015) Adaptive synchronization of fractional-order memristor-based neural networks with time delay. Nonlinear Dyn 82:1343–1354

    Article  MathSciNet  MATH  Google Scholar 

  11. Li R, Cao J, Xue C, Manivannan R (2021) Quasi-stability and quasi-synchronization control of quaternion-valued fractional-order discrete-time memristive neural networks. Appl Math Comput 395:125851

    MathSciNet  MATH  Google Scholar 

  12. Yang Z, Zhang J, Hu J, Mei J (2021) New results on finite-time stability for fractional-order neural networks with proportional delay. Neurocomputing 442:327–336

    Article  Google Scholar 

  13. You X, Song Q, Zhao Z (2020) Global Mittag-Leffler stability and synchronization of discrete-time fractional-order complex-valued neural networks with time delay. Neural Netw 122:382–394

    Article  MATH  Google Scholar 

  14. Gu Y, Wang H, Yu Y (2020) Synchronization for fractional-order discrete-time neural networks with time delays. Appl Math Comput 372:124995

    MathSciNet  MATH  Google Scholar 

  15. Pecora L, Carroll T (1990) Synchronization in chaotic systems. PRL 64:821

  16. Baluni S, Yadav V, Das S (2022) Quasi projective synchronization of time varying delayed complex valued Cohen-Grossberg neural networks. Inform Sciences 612:231–240

    Article  Google Scholar 

  17. Wang D, Huang L, Tang L, Zhuang J (2018) Generalized pinning synchronization of delayed Cohen-Grossberg neural networks with discontinuous activations. Neural Netw 104:80–92

    Article  MATH  Google Scholar 

  18. Xu Y, Li Y, Li W (2020) Adaptive finite-time synchronization control for fractional-order complex-valued dynamical networks with multiple weights. Commun Nonlinear Sci Numer Simul 85:105239

    Article  MathSciNet  MATH  Google Scholar 

  19. Ye R, Liu X, Zhang H (2018) Global Mittag-Leffler Synchronization for Fractional-Order BAM Neural Networks with Impulses and Multiple Variable Delays via Delayed-Feedback Control Strategy. Neural Process Lett 49:1–18

    Article  Google Scholar 

  20. Pratap A, Raja R, Sowmiya C, Bagdasar O, Cao J, Rajchakit G (2018) Robust generalized Mittag-Leffler synchronization of fractional order neural networks with discontinuous activation and impulses. Neural Netw 103:128–141

    Article  MATH  Google Scholar 

  21. Li H, Hu C, Cao J, Jiang H, Alsaedi A (2019) Quasi-projective and complete synchronization of fractional-order complex-valued neural networks with time delays. Neural Netw 118:102–109

    Article  MATH  Google Scholar 

  22. Pratap A, Raja R, Cao J, Rihan F, Seadawy A (2020) Quasi-pinning synchronization and stabilization of fractional order BAM neural networks with delays and discontinuous neuron activations. Chaos Solitons Fract 131:109491

    Article  MathSciNet  MATH  Google Scholar 

  23. Xiao J, Wen S, Yang X, Zhong S (2020) New approach to global Mittag-Leffler synchronization problem of fractional-order quaternion-valued BAM neural networks based on a new inequality. Neural Netw 122:320–337

    Article  MATH  Google Scholar 

  24. Yang T, Yang L (1996) The global stability of fuzzy cellular networks. IEEE Trans Circuits Syst I 43:880–883

    Article  MathSciNet  Google Scholar 

  25. Chen S, Li H, Kao Y, Zhang L, Hu C (2021) Finite-time stabilization of fractional-order fuzzy quaternion-valued BAM neural networks via direct quaternion approach. J Frankl Inst 358:7650–7673

    Article  MathSciNet  MATH  Google Scholar 

  26. Li H, Hu C, Zhang L, Jiang H, Cao J (2022) Complete and finite-time synchronization of fractional-order fuzzy neural networks via nonlinear feedback control. Fuzzy Sets Syst 443:50–69

    Article  MathSciNet  Google Scholar 

  27. Kumar A, Das S, Baluni S, Yadav V, Lu J (2022) Global quasi-synchronisation of fuzzy cellular neural networks with time varying delay and interaction terms. Int J Syst Sci. https://doi.org/10.1080/00207721.2022.2058109

  28. Ali M, Hymavathi M (2021) Synchronization of fractional order neutral type fuzzy cellular neural networks with discrete and distributed delays via state feedback control. Neural Process Lett 53:929–957

    Article  Google Scholar 

  29. Ali M, Narayanan G, Saroha S, Priya B, Thakur G (2021) Finite-time stability analysis of fractional-order memristive fuzzy cellular neural networks with time delay and leakage term. Math Comput Simulat 185:468–485

    Article  MathSciNet  MATH  Google Scholar 

  30. Tyagi S, Martha S (2020) Finite-time stability for a class of fractional-order fuzzy neural networks with proportional delay. Fuzzy Set Syst 381:68–77

    Article  MathSciNet  MATH  Google Scholar 

  31. Xiao J, Cheng J, Shi K, Zhang R (2021) A general approach to fixed-time synchronization problem for fractional-order multidimension-valued fuzzy neural networks based on memristor. IEEE Trans Fuzzy Syst 30:968–977

    Article  Google Scholar 

  32. Chen J, Li C, Yang X (2018) Asymptotic stability of delayed fractional-order fuzzy neural networks with impulse effects. J Frankl Inst 355:7595–7608

    Article  MathSciNet  MATH  Google Scholar 

  33. Adali T, Schreier P, Scharf L (2011) Complex-valued signal processing: The proper way to deal with impropriety. IEEE Trans Signal Proces 59:5101–5125

    Article  MathSciNet  MATH  Google Scholar 

  34. Pratap A, Raja R, Cao J, Huang C, Niezabitowski M, Bagdasar O (2021) Stability of discrete-time fractional-order time-delayed neural networks in complex field. Math Methods Appl Sci 44:419–440

    Article  MathSciNet  MATH  Google Scholar 

  35. Hu J, Wang J (2012) Global stability of complex-valued recurrent neural networks with time-delays. IEEE Trans Neural Netw Learn Syst 23:853–865

    Article  Google Scholar 

  36. Zhang C, Wang X, Wang S, Zhou W, Xia Z (2018) Finite-time synchronization for a class of fully complex-valued networks with coupling delay. IEEE Access 6:17923–17932

    Article  Google Scholar 

  37. Zhang C, Wang X, Unar S, Wang Y (2019) Finite-time synchronization of a class of nonlinear complex-valued networks with time-varying delays. Physica A 20:273–280

    Article  MathSciNet  MATH  Google Scholar 

  38. Abdeljawad T, Baleanu D (2017) Monotonicity analysis of a nabla discrete fractional operator with discrete Mittag-Leffler kernel. Chaos Soliton Fract 102:106–110

    Article  MathSciNet  MATH  Google Scholar 

  39. Hou T, Yu J, Hu C, Jiang H (2019) Finite-time synchronization of fractional-order complex-variable dynamic networks. IEEE Trans Syst Man Cybern 51:4297–4307

    Article  Google Scholar 

  40. Khan A, Tammer C, Zalinescu C (2015) Set-valued optimization: An Introduction with applications. Springer, Berlin

    Book  MATH  Google Scholar 

  41. Ma W, Li C, Wu Y, Wu Y (2017) Synchronization of fractional fuzzy cellular neural networks with interactions. Chaos 27:103106

    Article  MathSciNet  MATH  Google Scholar 

  42. Singh S, Kumar U, Das S, Cao J (2022) Global exponential stability of Inertial Cohen-Grossberg neural networks with time-varying delays via feedback and adaptive control schemes: Non-reduction order approach. Neural Process Lett. https://doi.org/10.1007/s11063-022-11044-9

  43. Baluni S, Das S, Yadav V, Cao J (2022) Lagrange \(\alpha \)-exponential synchronization of non-identical fractional-order complex-valued neural networks. Circ Syst Signal Pr 41:5632–5652

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant Nos. 12262035, 12261087), Tianshan Youth Program-Training Program for Excellent Young Scientific and Technological Talents (Grant No. 2019Q017).

Author information

Authors and Affiliations

  1. College of Mathematics and System Sciences, Xinjiang University, Urumqi, 830046, China

    Yingying Xu, Hong-Li Li, Long Zhang, Cheng Hu & Haijun Jiang

Authors
  1. Yingying Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hong-Li Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Long Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Cheng Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Haijun Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Yingying Xu: Methodology, Writing-original draft. Hong-Li Li: Supervision, Conceptualization, Methodology, Writing-review & editing, Funding acquisition. Long Zhang: Formal analysis, Methodology. Cheng Hu: Software. Haijun Jiang: Formal analysis.

Corresponding author

Correspondence to Hong-Li Li.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, Y., Li, HL., Zhang, L. et al. Quasi-Projective and Mittag-Leffler Synchronization of Discrete-Time Fractional-Order Complex-Valued Fuzzy Neural Networks. Neural Process Lett 55, 6657–6677 (2023). https://doi.org/10.1007/s11063-023-11153-z

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-023-11153-z

Keywords

Search

Navigation