iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://unpaywall.org/10.1007/S11063-020-10309-5
Exponential Synchronization of Complex-Valued Neural Networks Via Average Impulsive Interval Strategy | Neural Processing Letters Skip to main content
Springer Nature Link
Log in

Exponential Synchronization of Complex-Valued Neural Networks Via Average Impulsive Interval Strategy

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

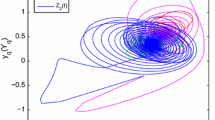
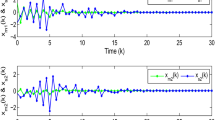
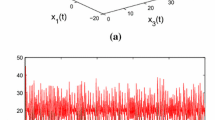
In this paper, the issue of the exponential synchronization for complex-valued neural networks with both discrete and distributed delays is investigated by applying impulsive control protocol. Based on the Lyapunov–Krasovskii function, average impulsive interval as well as the comparison principle, some simple verifiable sufficient criteria are established to guarantee the exponential synchronization between the master and the slave systems. Meanwhile, through the serious analysis of the networks systems, the exponential convergence rate can be specified. Additionally, a numerical example is finally given to illustrate the effectiveness of the proposed theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Xiong W, Ho D, Yu X (2016) Saturated finite interval iterative learning for tracking of dynamic systems with HNN-structural output. IEEE Trans Neural Netw Learn Syst 27:1578–1584

    Article  MathSciNet  Google Scholar 

  2. Wan X, Yang X, Tang R, Cheng Z (2019) Exponential synchronization of semi-Markovian coupled neural networks with mixed delays via tracker information and quantized output controller. Neural Netw 118:321–331

    Article  Google Scholar 

  3. Liu M, Jiang H, Hu C (2016) Synchronization of hybrid-coupled delayed dynamical networks via aperiodically intermittent pinning control. J Franklin Inst 353:2722–2742

    Article  MathSciNet  Google Scholar 

  4. Li C, Chen G (2004) Phase synchronization in small-world networks of chaotic oscillators. Physical A 341:73–79

    Article  MathSciNet  Google Scholar 

  5. Zhang S (2015) Impulsive complex projective synchronization in drive-response complex coupled dynamical networks. Nonlinear Dyn 79:147–161

    Article  MathSciNet  Google Scholar 

  6. Cai S, Li X, Jia Q, Liu Z (2016) Exponential cluster synchronization of hybrid-coupled impulsive delayed dynamical networks: average impulsive interval approach. Nonlinear Dyn 85:2405–2423

    Article  Google Scholar 

  7. Liu M, Jiang H, Hu C (2016) Finite-time synchronization of memristor-based Cohen–Grossberg neural networks with time-varying delays. Neurocomputing 194:1–9

    Article  Google Scholar 

  8. Ma Q, Wang Z, Lu J (2012) Finite-time synchronization for complex dynamical networks with time-varying delays. Nonlinear Dyn 70:841–845

    Article  MathSciNet  Google Scholar 

  9. Hirose A (1992) Dynamics of fully complex-valued neural networks. Electron Lett 28:1492–1494

    Article  Google Scholar 

  10. Jankowski S, Lozowski A, Zurada J (1996) Complex-valued multistate neural associative memory. IEEE Trans Neural Netw Learn Syst 7:1491–1496

    Article  Google Scholar 

  11. Liu J, Liu S, Sprott J (2016) Adaptive complex modified hybrid function projective synchronization of different dimensional complex chaos with uncertain complex parameters. Nonlinear Dyn 83:1109–1121

    Article  MathSciNet  Google Scholar 

  12. Liu D, Wu Z, Ye Q (2014) Adaptive impulsive synchronization of uncertain drive-response complex-variable chaotic systems. Nonlinear Dyn 75:209–216

    Article  MathSciNet  Google Scholar 

  13. Bao H, Park J (2016) Adaptive synchronization of complex-valued neural networks with time delay. In: 8th International conference on advanced computational intelligence

  14. Wu E, Yang X (2016) Adaptive synchronization of coupled nonidentical chaotic systems with complex variables and stochastic perturbations. Nonlinear Dyn 84:261–269

    Article  MathSciNet  Google Scholar 

  15. Liu M, Jiang H, Hu C (2016) Exponential stability of Cohen-Grossberg neural networks with impulse time window. Discrete Dyn Nat Soc ID:2762960

  16. Yang X, Yang Z (2014) Synchronization of TS fuzzy complex dynamical networks with time-varying impulsive delays and stochastic effects. Fuzzy Sets Syst 23:25–43

    Article  MathSciNet  Google Scholar 

  17. Yang X, Cao J, Qiu J (2015) Pth moment exponential stochastic synchronization of coupled memristor-based neural networks with mixed delays via delayed impulsive control. Neural Netw 65:80–91

    Article  Google Scholar 

  18. Yang X, Lu J, Song Q (2018) Synchronization of uncertain hybrid switching and impulsive complex networks. Appl Math Model 59:379–392

    Article  MathSciNet  Google Scholar 

  19. Lu J, Ho D, Cao J (2011) Exponential synchronization of linearly coupled neural networks with impulsive disturbances. IEEE Trans Neural Netw Learn Syst 22:29–335

    Google Scholar 

  20. Yang X, Huang C, Zhu Q (2011) Synchronization of switched neural networks with mixed delays via impulsive control. Chaos Solitons Fractals 44:817–826

    Article  MathSciNet  Google Scholar 

  21. Rakkiyappan R, Chandrasekar A, Lakshmanan S, Park J, Jung H (2013) Effects of leakage time-varying delays in Markovian jump neural networks with impulse control. Neurocomputing 121:365–378

    Article  Google Scholar 

  22. Cai S, Zhou P, Liu Z (2014) Synchronization analysis of directed complex networks with time-delayed dynamical nodes and impulsive effects. Nonlinear Dyn 76:1677–1691

    Article  MathSciNet  Google Scholar 

  23. Chen W, Jiang Z, Zhong J, Lu X (2014) On designing decentralized impulsive controllers for synchronization of complex dynamical networks with nonidentical nodes and coupling delays. J Frankl Inst 351:4084–4110

    Article  MathSciNet  Google Scholar 

  24. Song Q, Yan H, Zhao Z, Liu Y (2016) Global exponential stability of impulsive complex-valued neural networks with both asynchronous time-varying and continuously distributed delays. Neural networks 81:1–10

    Article  Google Scholar 

  25. Song Q, Yan H, Zhao Z, Liu Y (2016) Global exponential stability of complex-valued neural networks with both time-varying delays and impulsive effects. Neural Netw 79:108–116

    Article  Google Scholar 

  26. He W, Qian F, Cao J (2017) Pinning-controlled synchronization of delayed neural networks with distributed-delay coupling via impulsive control. Neural Netw 85:1–9

    Article  Google Scholar 

  27. Xu Y, Zhou W, Fang J, Wen S, Pan L (2016) Adaptive synchronization of stochastic time-varying delay dynamical networks with complex-variable systems. Nonlinear Dyn 81:1717–1726

    Article  MathSciNet  Google Scholar 

  28. Liu Y, Wang Z, Liu X (2006) Global exponential stability of generalized recurrent neural networks with discrete and distributed delays. Neural Netw 19:667–675

    Article  Google Scholar 

  29. Li H, Gao H, Shi P (2010) New passivity analysis for neural networks with discrete and distributed delays. IEEE Trans Neural Netw Learn Syst 21:842–1847

    Google Scholar 

  30. Jiang P, Zeng Z, Che J (2015) Almost periodic solutions for a memristor-based neural networks with leakage, time-varying and distributed delays. Neural Netw 68:34–45

    Article  Google Scholar 

  31. Guan Z, Liu Z, Feng G, Wang Y (2010) Synchronization of complex dynamical networks with time-varying delays via impulsive distributed control. IEEE Trans Circ Syst I Regul Pap 57:2182–2195

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work was supported by the Research Fund Project of Zhoukou Normal University (Grant No. ZKNUC 2018009), the Scientific Research Program of the Higher Education Institution of Xinjiang (Grants Nos. XJEDU2017T001, XJEDU2018Y004), the Doctoral Foundation of Xinjiang University (Grant No. 62008032), and the National Natural Science Foundation of China (Grants Nos. U1703262, 61563048, 11702237), the Tianshan Xuesong Program (Grant No. 2018XS02).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Zhoukou Normal University, Zhoukou, 466001, Henan, People’s Republic of China

    Mei Liu & Zhanfeng Li

  2. College of Mathematics and System Sciences, Xinjiang University, Urumqi, 830046, Xinjiang, People’s Republic of China

    Haijun Jiang, Cheng Hu & Zhiyong Yu

Authors
  1. Mei Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhanfeng Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Haijun Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Cheng Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Zhiyong Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mei Liu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, M., Li, Z., Jiang, H. et al. Exponential Synchronization of Complex-Valued Neural Networks Via Average Impulsive Interval Strategy. Neural Process Lett 52, 1377–1394 (2020). https://doi.org/10.1007/s11063-020-10309-5

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-020-10309-5

Keywords

Search

Navigation