iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://unpaywall.org/10.1007/S11042-022-12248-W
A genetic programming approach for searching on nearest neighbors graphs | Multimedia Tools and Applications Skip to main content

Advertisement

Springer Nature Link
Log in

A genetic programming approach for searching on nearest neighbors graphs

  • Published:
Multimedia Tools and Applications Aims and scope Submit manuscript

Abstract

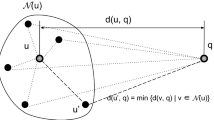
Nearest neighbors graphs have gained a lot of attention from the information retrieval community since they were demonstrated to outperform classical approaches in the task of approximate nearest neighbor search. These approaches, firstly, index feature vectors by using a graph-based data structure. Then, for a given query, the search is performed by traversing the graph in a greedy-way, moving in each step towards the neighbor of the current vertex that is closer to the query (based on a distance function). However, local topological properties of vertices could be also considered at the moment of deciding the next vertex to be explored. In this work, we introduce a Genetic Programming framework that combines topological properties along with the distance to the query, aiming to improve the selection of the next vertex in each step of graph traversal and, therefore, reduce the number of vertices explored (scan rate) to find the true nearest neighbors. Experimental results, conducted over three large collections of feature vectors and four different graph-based techniques, show significant gains of the proposed approach over classic graph-based search algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Notes

  1. ANN benchmark: https://github.com/erikbern/ann-benchmarks (As of June 2021).

  2. GloVe: https://nlp.stanford.edu/projects/glove/ (As of June 2021).

  3. YFCC100M: http://multimedia-commons.s3-website-us-west-2.amazonaws.com (As of June 2021).

  4. BIGANN benchmark: http://corpus-texmex.irisa.fr (As of June 2021).

  5. KGraph: https://github.com/aaalgo/kgraph (As of June 2021).

  6. NMSLIB: https://github.com/nmslib/nmslib (As of June 2021).

References

  1. Albarracín J.F.H., Ferreira E., dos Santos J.A., da Silva Torres R (2017) Fusion of genetic-programming-based indices in hyperspectral image classification tasks. In: Proceeding of the IEEE international geoscience and remote sensing symposium, pp. 554–557

  2. Albarracín J.F.H., Oliveira R., Hirota M., dos Santos J.A., da Silva Torres R (2020) A soft computing approach for selecting and combining spectral bands. Remote Sens 12(4):2267–0000. https://www.mdpi.com/769804

    Article  Google Scholar 

  3. Andoni A., Indyk P. (2008) Near-optimal hashing algorithms for approximate nearest neighbor in high dimensions. Commun ACM 51(1):117–122

    Article  Google Scholar 

  4. André F., Kermarrec A.M., Le Scouarnec N. (2017) Accelerated nearest neighbor search with quick adc. In: Proceedings of the 2017 ACM on International Conference on Multimedia Retrieval, ICMR’2017, pp. 159–166, ACM, New York, NY, USA

  5. Aumüller M., Bernhardsson E., Faithfull A. Beecks C., Borutta F., Kröger P., Seidl T. (eds) (2017) Ann-benchmarks: a benchmarking tool for approximate nearest neighbor algorithms. Springer International Publishing, Cham

  6. Babenko A., Lempitsky V. (2014) Additive quantization for extreme vector compression. In: Proceedings of the Conference on Computer Vision and Pattern Recognition, pp. 931–938

  7. Babenko A., Lempitsky V. (2015) The inverted multi-index. IEEE Trans Pattern Anal Mach Intell 37(6):1247–1260

    Article  Google Scholar 

  8. Bawa M., Condie T., Ganesan P. (2005) LSH forest: Self-tuning indexes for similarity search. In: Proceedings of the 14th International Conference on World Wide Web, WWW’2005, pp. 651–660

  9. Bentley J.L. (1975) Multidimensional binary search trees used for associative searching. Commun ACM 18(9):509–517

    Article  Google Scholar 

  10. Chiu C.Y., Chiu J.S., Markchit S., Chou S.H. (2019) Effective product quantization-based indexing for nearest neighbor search. Multimed Tools Appl 78(3):2877–2895

    Article  Google Scholar 

  11. Costa L.d.F., Rodrigues F.A., Travieso G., Villas Boas P.R. (2007) Characterization of complex networks: a survey of measurements. Adv Phys 56(1):167–242

    Article  Google Scholar 

  12. Dasgupta S., Freund Y. (2008) Random projection trees and low dimensional manifolds. In: Proceedings of the 40th Annual ACM Symposium on Theory of Computing, STOC’2008, pp. 537–546

  13. da S., Torres R., Falcão A.X., Gonċalves M. A., Papa J.P., Zhang B., Fan W., Fox E.A. (2009) A genetic programming framework for content-based image retrieval. Pattern Recogn 42(2):283–292

    Article  Google Scholar 

  14. de Carvalho M.G., Laender A.H.F., Gonċalves M.A., da Silva A.S. (2012) A genetic programming approach to record deduplication. IEEE Trans Knowl Data Eng 24(3):399–412

    Article  Google Scholar 

  15. Dong W., Moses C., Li K. (2011) Efficient k-nearest neighbor graph construction for generic similarity measures. In: Proceedings of the 20th International Conference on World Wide Web, WWW’2011, pp. 577–586

  16. Efstathiades C., Efentakis A., Pfoser D. (2016) Efficient processing of relevant nearest-neighbor queries. ACM Trans Spat Algorithms Syst 2(3):1–28

    Article  Google Scholar 

  17. Ge T., He K., Ke Q., Sun J. (2013) Optimized product quantization for approximate nearest neighbor search. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 2946–2953

  18. Goldberg A.V., Harrelson C. (2005) Computing the shortest path: A* search meets graph theory SODA’2005

  19. Gonzalez-Lopez J., Ventura S., Cano A. (2018) Distributed nearest neighbor classification for large-scale multi-label data on spark. Futur Gener Comput Syst 87:66–82

    Article  Google Scholar 

  20. Gubichev A., Bedathur S., Seufert S., Weikum G. (2010) Fast and accurate estimation of shortest paths in large graphs

  21. Guttman A. (1984) R-trees: a dynamic index structure for spatial searching. In: Proceedings of the 1984 ACM SIGMOD International Conference on Management of Data, SIGMOD’1984, pp. 47–57, ACM, New York, NY, USA

  22. Harwood B. (2016) Drummond, T.: FANNG: Fast approximate nearest neighbour graphs. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 5713–5722

  23. Houle M.E., Ma X., Oria V., Sun J. (2014) Improving the quality of k-nn graphs for image databases through vector sparsification. In: Proceedings of International Conference on Multimedia Retrieval, ICMR’2014, pp. 89:89–89:96. ACM

  24. Indyk P., Motwani R. (1998) Approximate nearest neighbors: Towards removing the curse of dimensionality. In: Proceedings of the 30th Annual ACM Symposium on Theory of Computing, pp. 604–613

  25. Iwasaki M. (2016) Pruned bi-directed k-nearest neighbor graph for proximity search. Springer International Publishing, Cham

    Google Scholar 

  26. Jebari K. (2013) Selection methods for genetic algorithms. Int J Emerg Sci 3:333–344

    Google Scholar 

  27. Jegou H., Douze M., Schmid C. (2011) Product quantization for nearest neighbor search. IEEE Trans Pattern Anal Mach Intell 33(1):117–128

    Article  Google Scholar 

  28. Ji T., Liu X., Deng C., Huang L., Lang B. (2014) Query-adaptive hash code ranking for fast nearest neighbor search. In: Proceedings of the 22nd ACM International Conference on Multimedia, MM’2014, pp. 1005–1008, ACM, New York, NY, USA

  29. Kalantidis Y., Avrithis Y. (2014) Locally optimized product quantization for approximate nearest neighbor search. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 2329–2336

  30. Koza J.R. (1992) Genetic Programming: on the programming of computers by means of natural selection, vol 1. MIT press, Cambridge

    MATH  Google Scholar 

  31. Lacerda A., Cristo M., Gonçalves M.A., Fan W., Ziviani N., Ribeiro-Neto B. (2006) Learning to advertise. In: Proceedings of the 29th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, SIGIR’2006, pp. 549–556, ACM, New York, NY, USA

  32. Li J., Lan X., Wang J., Yang M., Zheng N. (2017) Fast additive quantization for vector compression in nearest neighbor search. Multimed Tools Appl 76(22):23273–23289

    Article  Google Scholar 

  33. Liu J., Li M., Liu Q., Lu H., Ma S. (2009) Image annotation via graph learning. Pattern Recogn 42(2):218–228

    Article  Google Scholar 

  34. Lowe D.G. (1999) Object recognition from local scale-invariant features. In: Proceedings of the Seventh IEEE International Conference on Computer Vision, vol. 2, pp. 1150–1157 vol.2.

  35. Lv Q., Josephson W., Wang Z., Charikar M., Li K. (2007) Multi-probe LSH: Efficient indexing for high-dimensional similarity search. In: Proceedings of the 33rd International Conference on Very Large Data Bases, VLDB’2007, pp. 950–961

  36. Malkov Y.A., Ponomarenko A., Logvinov A., Krylov V. (2014) Approximate nearest neighbor algorithm based on navigable small world graphs. Inf Syst 45:61–68

    Article  Google Scholar 

  37. Malkov Y.A., Yashunin D.A. (2016)

  38. Muja M., Lowe D.G. (2009) Fast approximate nearest neighbors with automatic algorithm configuration. In: Proceedings of the International Conference on Computer Vision Theory and Application, pp. 331–340

  39. Muja M., Lowe D.G. (2014) Scalable nearest neighbor algorithms for high dimensional data. IEEE Trans Pattern Anal Mach Intell 36(11):2227–2240

    Article  Google Scholar 

  40. Papadias D. (2000) Hill climbing algorithms for content-based retrieval of similar configurations. In: Proceedings of the 23rd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, SIGIR’2000, pp. 240–247, ACM, New York, NY, USA

  41. Pennington J., Socher R., Manning C. (2014) Glove: Global vectors for word representation. In: Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing, pp. 1532–1543

  42. Popescu A., Spyromitros-Xioufis E., Papadopoulos S., Le Borgne H., Kompatsiaris I. (2015) Toward an automatic evaluation of retrieval performance with large scale image collections. In: Proceedings of the 2015 Workshop on Community-Organized Multimodal Mining: Opportunities for Novel Solutions, MMCommons’2015, pp. 7–12, ACM, New York, NY, USA

  43. Potamias M., Bonchi F., Castillo C., Gionis A. (2009) Fast shortest path distance estimation in large networks. In: Proceedings of the 18th ACM conference on Information and knowledge management, CIKM’2009, pp. 867–876

  44. Silpa-Anan C., Hartley R. (2008) Optimised kd-trees for fast image descriptor matching. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 1–8

  45. Sproull R.F. (1991) Refinements to nearest-neighbor searching in k-dimensional trees. Algorithmica 6(1-6):579–589

    Article  MathSciNet  Google Scholar 

  46. Su F., Xue L. (2015) Graph learning on k nearest neighbours for automatic image annotation. In: Proceedings of the 5th ACM on International Conference on Multimedia Retrieval, ICMR’2015, pp. 403–410, ACM, New York, NY, USA

  47. Tang J., Hong R., Yan S., Chua T.S., Qi G.J., Jain R. (2011) Image annotation by knn-sparse graph-based label propagation over noisily tagged web images. ACM Trans Intell Syst Technol 2(2):14:1–1415

    Article  Google Scholar 

  48. Tretyakov K., Armas-Cervantes A., García-bañuelos L., Vilo J., Dumas M. (2011) Fast fully dynamic landmark-based estimation of shortest path distances in very large graphs. In: Proceedings of the 20th ACM International Conference on Information and Knowledge Management, CIKM’2011, pp. 1785–1794, Association for Computing Machinery, New York, NY, USA

  49. Vargas J.A. (2020) Large-scale indexing of high dimensional data via nearest neighbors graphs. Ph.D. thesis, University of Campinas, São Paulo, Brazil

  50. Vargas J.A., Dias Z., da S., Torres R. (2019) A genetic programming approach for searching on nearest neighbors graphs. In: Proceedings of the 2019 on International Conference on Multimedia Retrieval, ICMR ’19, pp. 43–47, ACM, New York, NY, USA

  51. Vargas J.A., Gonçalves M.A., Dias Z., da S., Torres R. (2019) Hierarchical clustering-based graphs for large scale approximate nearest neighbor search. Pattern Recogn 106970:96

    Google Scholar 

  52. Wang M., Zhou W., Tian Q., Pu J., Li H. (2017) Deep supervised quantization by self-organizing map. In: Proceedings of the 25th ACM International Conference on Multimedia, MM’2017, pp. 1707–1715, ACM, New York, NY, USA

  53. Xiaokang F., Jiangtao C., Hui L., Yingfan L. (2019) An efficient lsh indexing on discriminative short codes for high-dimensional nearest neighbors. Multimed Tools Appl 78(17):24407–24429

    Article  Google Scholar 

  54. Yianilos P.N. (1993) Data structures and algorithms for nearest neighbor search in general metric spaces. In: Proceedings of the 4th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 311–321

Download references

Acknowledgements

Authors are grateful to CNPq (grants #307560/2016-3, #400487/2016-0, #425340/ 2016-3, #304380/2018-0, and #422593/2018-4), CAPES (grant #88881.145912/2017-01), FAPESP (grants #2014/12236-1, #2015/24494-8, #2016/50250-1, #2017/20945-0, #2015/11937-9, #2017/11618-6, #2017/12646-3, and #2017/16246-0) and the FAPESP-Microsoft Virtual Institute (grants #2013/50155-0, #2013/50169-1, and #2014/50715-9). This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001. The authors are also grateful to the NFR SmartPlan and TwinFjord projects.

Author information

Authors and Affiliations

  1. University of Campinas, Campinas, Brazil

    Javier A. Vargas Muñoz & Zanoni Dias

  2. Norwegian University of Science and Technology, Larsgårdsvegen 2, 6009, Ålesund, Norway

    Ricardo da Silva Torres

Authors
  1. Javier A. Vargas Muñoz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zanoni Dias
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ricardo da Silva Torres
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Javier A. Vargas Muñoz.

Ethics declarations

Conflict of Interests

The authors declare that they have no conflict of interest.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Muñoz, J.A.V., Dias, Z. & Torres, R.d.S. A genetic programming approach for searching on nearest neighbors graphs. Multimed Tools Appl 81, 23449–23472 (2022). https://doi.org/10.1007/s11042-022-12248-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11042-022-12248-w

Keywords

Search

Navigation