iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://unpaywall.org/10.1007/S10957-024-02532-0
An Empirical Quantile Estimation Approach for Chance-Constrained Nonlinear Optimization Problems | Journal of Optimization Theory and Applications Skip to main content
Springer Nature Link
Log in

An Empirical Quantile Estimation Approach for Chance-Constrained Nonlinear Optimization Problems

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

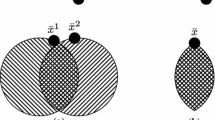
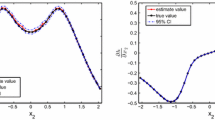
We investigate an empirical quantile estimation approach to solve chance-constrained nonlinear optimization problems. Our approach is based on the reformulation of the chance constraint as an equivalent quantile constraint to provide stronger signals on the gradient. In this approach, the value of the quantile function is estimated empirically from samples drawn from the random parameters, and the gradient of the quantile function is estimated via a finite-difference approximation on top of the quantile-function-value estimation. We establish a convergence theory of this approach within the framework of an augmented Lagrangian method for solving general nonlinear constrained optimization problems. The foundation of the convergence analysis is a concentration property of the empirical quantile process, and the analysis is divided based on whether or not the quantile function is differentiable. In contrast to the sampling-and-smoothing approach used in the literature, the method developed in this paper does not involve any smoothing function and hence the quantile-function gradient approximation is easier to implement and there are less accuracy-control parameters to tune. We demonstrate the effectiveness of this approach and compare it with a smoothing method for the quantile-gradient estimation. Numerical investigation shows that the two approaches are competitive for certain problem instances.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. van Ackooij, W., Henrion, R.: Gradient formulae for nonlinear probabilistic constraints with Gaussian and Gaussian-like distributions. SIAM J. Optim. 24(4), 1864–1889 (2014). https://doi.org/10.1137/130922689

    Article  MathSciNet  Google Scholar 

  2. Birgin, E.G., Castillo, R.A., Martínez, J.M.: Numerical comparison of augmented Lagrangian algorithms for nonconvex programs. Comput. Optim. Appl. 31, 31–55 (2012). https://doi.org/10.1007/s10589-005-1066-7

    Article  Google Scholar 

  3. Birgin, E.G., Fernández, D., Martínez, J.M.: The boundedness of penalty parameters in an augmented Lagrangian method with constrained subproblems. Optim. Methods Softw. 27(6), 1001–1024 (2012). https://doi.org/10.1080/10556788.2011.556634

    Article  MathSciNet  Google Scholar 

  4. Birgin, E.G., Martínez, J.M.: Practical augmented Lagrangian methods for constrained optimization. Soc. Ind. Appl. Math. (2014). https://doi.org/10.1137/1.9781611973365

    Article  Google Scholar 

  5. Calafiore, G., Campi, M.C.: Uncertain convex programs: randomized solutions and confidence levels. Math. Prog. 102, 25–46 (2005). https://doi.org/10.1007/s10107-003-0499-y

    Article  MathSciNet  Google Scholar 

  6. Calafiore, G., Campi, M.C.: The scenario approach to robust control desgin. IEEE Trans. Autom. Control 51, 742–753 (2006). https://doi.org/10.1109/TAC.2006.875041

    Article  Google Scholar 

  7. Campi, M.C., Garatti, S.: A sampling-and-discarding approach to chance-constrained optimization: feasibility and optimality. J. Optim. Theory Appl. 148, 257–280 (2011). https://doi.org/10.1007/s10957-010-9754-6

    Article  MathSciNet  Google Scholar 

  8. Cao, Y., Zavala, V.M.: A sigmoidal approximation for chance-constrained nonlinear programs. Technical Report, arXiv:2004.02402 (2020). https://doi.org/10.48550/arXiv.2004.02402

  9. Charnes, A., Cooper, W.W., Symonds, G.H.: Cost horizons and certainty equivalents: an approach to stochastic programming of heating oil. Manag. Sci. 4(3), 235–263 (1958). https://doi.org/10.1287/mnsc.4.3.235

    Article  Google Scholar 

  10. Csörgő, M., Révész, P.: Strong approximation of the quantile process. Ann. Stat. 6(4), 882–894 (1978). https://doi.org/10.1214/aos/1176344261

    Article  MathSciNet  Google Scholar 

  11. Curtis, F.E., Wächter, A., Zavala, V.M.: A sequential algorithm for solving nonlinear optimization problems with chance constraints. SIAM J. Optim. 28(1), 930–958 (2018). https://doi.org/10.1137/19M1261985

    Article  MathSciNet  Google Scholar 

  12. Davis, D., Drusvyatskiy, D.: Stochastic subgradient method converges at the rate \(O(k^{-1/4})\) on weakly convex functions. Technical Report, arXiv:1802.02988 (2018). https://doi.org/10.48550/arXiv.1802.02988

  13. Durrett, R.: Probability: Theory and Examples. Cambridge University Press, Cambridge (2019). https://doi.org/10.1017/9781108591034

    Book  Google Scholar 

  14. Garnier, J., Omrane, A., Rouchdy, Y.: Asymptotic formulas for the derivatives of probability functions and their Monte Carlo estimations. Eur. J. Oper. Res. 198(3), 848–858 (2009). https://doi.org/10.1016/j.ejor.2008.09.026

    Article  MathSciNet  Google Scholar 

  15. Geletu, A., Hoffmann, A., Klöppel, M., Li, P.: An inner-outer approximation approach to chance constrained optimization. SIAM J. Optim. 27(3), 1834–1857 (2017). https://doi.org/10.1137/19M1261985

    Article  MathSciNet  Google Scholar 

  16. Henrion, R., Möller, A.: A gradient formula for linear chance constraints under Gaussian distribution. Math. Oper. Res. 37(3), 475–488 (2012). https://doi.org/10.1287/moor.1120.0544

    Article  MathSciNet  Google Scholar 

  17. Hong, L.J.: Estimating quantile sensitivities. Oper. Res. 57(1), 118–130 (2009). https://doi.org/10.1287/opre.1080.0531

    Article  MathSciNet  Google Scholar 

  18. Hu, J., Peng, Y., Zhang, G., Zhang, Q.: A stochastic approximation method for simulation-based quantile optimization. INFORMS J. Comput. (2022). https://doi.org/10.1287/ijoc.2022.1214

    Article  MathSciNet  Google Scholar 

  19. Jiang, R., Guan, Y.: Data-driven chance constrained stochastic program. Math. Program. 158, 291–327 (2016). https://doi.org/10.1007/s10107-015-0929-7

    Article  MathSciNet  Google Scholar 

  20. Kannan, R., Luedtke, J.R.: A stochastic approximation method for approximating the efficient frontier of chance-constrained nonlinear programs. Math. Program. Comput. 13, 705–751 (2021). https://doi.org/10.1007/s12532-020-00199-y

    Article  MathSciNet  Google Scholar 

  21. Kibzun, A.I., Uryas’ev, S.: Differentiation of probability functions: the transformation method. Comput. Math. Appl. 30(3), 361–382 (1995). https://doi.org/10.1016/0898-1221(95)00113-1

    Article  MathSciNet  Google Scholar 

  22. Kibzun, A.I., Uryas’ev, S.: Differentiability of probability function. Stoch. Anal. Appl. 16(6), 1101–1128 (1998). https://doi.org/10.1080/07362999808809581

    Article  MathSciNet  Google Scholar 

  23. Küçükyavuz, S.: On mixing sets arising in chance-constrained programming. Math. Program. 132, 31–56 (2012). https://doi.org/10.1007/s10107-010-0385-3

    Article  MathSciNet  Google Scholar 

  24. Larson, J., Billups, S.C.: Stochastic derivative-free optimization using a trust region framework. Comput. Optim. Appl. 64(3), 619–645 (2016). https://doi.org/10.1007/s10589-016-9827-z

    Article  MathSciNet  Google Scholar 

  25. Liu, J., Lisser, A., Chen, Z.: Distributionally robust chance constrained geometric optimization. Math. Oper. Res. (2022). https://doi.org/10.1287/moor.2021.1233

    Article  MathSciNet  Google Scholar 

  26. Liu, X., Küçükyavuz, S., Luedtke, J.: Decomposition algorithms for two-stage chance-constrained programs. Math. Program. 157, 219–243 (2016). https://doi.org/10.1007/s10107-014-0832-7

    Article  MathSciNet  Google Scholar 

  27. Lodi, A., Malaguti, E., Nannicini, G., Thomopulos, D.: Nonlinear chance-constrained problems with applications to hydro scheduling. Math. Program. 191, 405–444 (2022). https://doi.org/10.1007/s10107-019-01447-3

    Article  MathSciNet  Google Scholar 

  28. Loève, M.: On almost sure convergence. Berkeley Symposium on Mathematical Statistics and Probability 2, 279–303 (1951). https://projecteuclid.org/ebook/Download?urlid=bsmsp/1200500235&isFullBook=false

  29. Luedtke, J.: A branch-and-cut decomposition algorithm for solving chance-constrained mathematical programs with finite support. Math. Program. 146, 219–244 (2014). https://doi.org/10.1007/s10107-013-0684-6

    Article  MathSciNet  Google Scholar 

  30. Luedtke, J., Ahmed, S.: A sample approximation approach for optimization with probabilistic constraints. SIAM J. Optim. 19(2), 674–699 (2008). https://doi.org/10.1137/070702928

    Article  MathSciNet  Google Scholar 

  31. Luedtke, J., Ahmed, S., Nemhauser, G.L.: An integer programming approach for linear programs with probabilistic constraints. Math. Program. 122, 247–272 (2010). https://doi.org/10.1007/s10107-008-0247-4

    Article  MathSciNet  Google Scholar 

  32. Luo, F., Larson, J.: Quantile optimization software (2023). https://doi.org/10.5281/zenodo.10044073

  33. Mangasarian, O., Fromovitz, S.: The Fritz John necessary optimality conditions in the presence of equality and inequality constraints. J. Math. Anal. Appl. 17(1), 37–47 (1967). https://doi.org/10.1016/0022-247X(67)90163-1

    Article  MathSciNet  Google Scholar 

  34. Nemirovski, A., Shapiro, A.: Scenario approximation of chance constraints. In: Calafiore, G., Dabbene, F. (eds.) Probab. Random. Methods Des. Under Uncertainty, pp. 3–48. Springer, London (2005). https://doi.org/10.1007/1-84628-095-8_1

    Chapter  Google Scholar 

  35. Peña-Ordieres, A., Luedtke, J.R., Wächter, A.: Solving chance-constrained problems via a smooth sample-based nonlinear approximation. SIAM J. Optim. 30(3), 2221–2250 (2020). https://doi.org/10.1137/19M1261985

    Article  MathSciNet  Google Scholar 

  36. Peng, Y., Fu, M.C., Heidergott, B., Lam, H.: Maximum likelihood estimation by Monte Carlo simulation: toward data-driven stochastic modeling. Oper. Res. 68(6), 1896–1912 (2020). https://doi.org/10.1287/opre.2019.1978

    Article  MathSciNet  Google Scholar 

  37. Pflug, G.C., Weisshaupt, H.: Probability gradient estimation by set-valued calculus and applications in network design. SIAM J. Optim. 15(3), 898–914 (2005). https://doi.org/10.1137/S1052623403431639

    Article  MathSciNet  Google Scholar 

  38. Prékopa, A.: On probabilistic constrained programming. In: Proceedings of the Princeton Symposium on Mathematical Programming, pp. 113–138 (1970). https://doi.org/10.1515/9781400869930-009

  39. Qi, L., Wei, Z.: On the constant positive linear independence condition and its application to SQP methods. SIAM J. Optim. 10(4), 963–981 (2000). https://doi.org/10.1137/S1052623497326629

    Article  MathSciNet  Google Scholar 

  40. Tong, S., Subramanyam, A., Rao, V.: Optimization under rare chance constraints. SIAM J. Optim. 32(2), 930–958 (2022). https://doi.org/10.1137/20M1382490

    Article  MathSciNet  Google Scholar 

  41. Uryas’ev, S.: Derivatives of probability functions and integrals over sets given by inequalities. J. Comput. Appl. Math. 56(1), 197–223 (1994). https://doi.org/10.1016/0377-0427(94)90388-3

    Article  MathSciNet  Google Scholar 

  42. Wild, S.M.: Solving derivative-free nonlinear least squares problems with POUNDERS. In: Terlaky, T., Anjos, M.F., Ahmed, S. (eds.) Advances and Trends in Optimization with Engineering Applications, pp. 529–540. SIAM, Philadelphia (2017). https://doi.org/10.1137/1.9781611974683.ch40

    Chapter  Google Scholar 

  43. Xie, W.: On distributionally robust chance constrained programs with Wasserstein distance. Math. Program. 186, 115–155 (2021). https://doi.org/10.1007/s10107-019-01445-5

    Article  MathSciNet  Google Scholar 

  44. Xie, W., Ahmed, S.: On quantile cuts and their closure for chance constrained optimization problems. Math. Program. 172, 621–646 (2018). https://doi.org/10.1007/s10107-017-1190-z

    Article  MathSciNet  Google Scholar 

  45. Xu, Y.: Primal-dual stochastic gradient method for convex programs with many functional constraints. SIAM J. Optim. 30(2), 1664–1692 (2020). https://doi.org/10.1137/18M1229869

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

Careful comments from three anonymous referees led to substantial improvements of the main theoretical result and quality of the numerical section. This work was supported by the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, Scientific Discovery through Advanced Computing (SciDAC) Program through the FASTMath Institute under Contract No. DE-AC02-06CH11357.

Author information

Authors and Affiliations

  1. Uber Technologies, San Francisco, USA

    Fengqiao Luo

  2. Mathematics and Computer Science Division, Argonne National Laboratory, Lemont, USA

    Jeffrey Larson

Authors
  1. Fengqiao Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jeffrey Larson
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fengqiao Luo.

Additional information

Communicated by Luis Zuluaga.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Luo, F., Larson, J. An Empirical Quantile Estimation Approach for Chance-Constrained Nonlinear Optimization Problems. J Optim Theory Appl 203, 767–809 (2024). https://doi.org/10.1007/s10957-024-02532-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-024-02532-0

Keywords

Mathematics Subject Classification

Search

Navigation