iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://unpaywall.org/10.1007/S10916-016-0600-8
Hypergraph Based Feature Selection Technique for Medical Diagnosis | Journal of Medical Systems Skip to main content

Advertisement

Springer Nature Link
Log in

Hypergraph Based Feature Selection Technique for Medical Diagnosis

  • Systems-Level Quality Improvement
  • Published:
Journal of Medical Systems Aims and scope Submit manuscript

Abstract

The impact of internet and information systems across various domains have resulted in substantial generation of multidimensional datasets. The use of data mining and knowledge discovery techniques to extract the original information contained in the multidimensional datasets play a significant role in the exploitation of complete benefit provided by them. The presence of large number of features in the high dimensional datasets incurs high computational cost in terms of computing power and time. Hence, feature selection technique has been commonly used to build robust machine learning models to select a subset of relevant features which projects the maximal information content of the original dataset. In this paper, a novel Rough Set based K – Helly feature selection technique (RSKHT) which hybridize Rough Set Theory (RST) and K – Helly property of hypergraph representation had been designed to identify the optimal feature subset or reduct for medical diagnostic applications. Experiments carried out using the medical datasets from the UCI repository proves the dominance of the RSKHT over other feature selection techniques with respect to the reduct size, classification accuracy and time complexity. The performance of the RSKHT had been validated using WEKA tool, which shows that RSKHT had been computationally attractive and flexible over massive datasets.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Uzer, M.S., Yilmaz, N., and Inan, O., Feature selection method based on artificial bee colony algorithm and support vector machines for medical datasets classification. Sci. World J. 2013:1–10, 2013. doi:10.1155/2013/419187.

    Article  Google Scholar 

  2. Li, H., Feature selection for high-risk pattern discovery in medical data. University of Cincinnati, Dissertation, 2012.

    Google Scholar 

  3. Fan, Y.J., and Chaovalitwongse, W.A., Optimizing feature selection to improve medical diagnosis. Ann. Oper. Res. 174:169–183, 2010. doi:10.1007/s10479–008-0506-z.

    Article  Google Scholar 

  4. Pardalos, P.M., Boginski, V.L., and Alkis, V., Data mining in biomedicine. Springer science & business media: New York, 2008.

    Google Scholar 

  5. Hammer, P.L., and Bonates, T.O., Logical analysis of data—an overview: from combinatorial optimization to medical applications. Ann. Oper. Res. 148:203–225, 2006. doi:10.1007/s10479–006-0075-y.

    Article  Google Scholar 

  6. Saastamoinen K, Ketola J (2006) Medical data classification using logical similarity based measures. IEEE Conference on Cybernetics and Intelligent Systems. 1–5. doi:10.1109/ICCIS.2006.252362

  7. Tsirogiannis, G.L., Frossyniotis, D., Stoitsis, J., Golemati, S., Stafylopatis, A., and Nikita, K.S., Classification of medical data with a robust multi-level combination scheme. IEEE International Joint Conference on Neural Networks. 3:2483–2487, 2004. doi:10.1109/IJCNN.2004.1381020.

    Google Scholar 

  8. Huang, M.L., Hung, Y.H., and Chen, W.Y., Neural network classifier with entropy based feature selection on breast cancer diagnosis. J. Med. Syst. 34:865–873, 2010. doi:10.1007/s10916–009-9301-x.

    Article  PubMed  Google Scholar 

  9. Raymer, M.L., Doom, T.E., Kuhn, L.A., and Punch, W.F., Knowledge discovery in medical and biological datasets using a hybrid Bayes classifier/evolutionary algorithm. IEEE Trans. Syst. Man Cybern. 33:802–813, 2003. doi:10.1109/TSMCB.2003.816922.

    Article  CAS  Google Scholar 

  10. Dash, M., and Liu, H., Feature selection for classification. Intelligent Data Analysis. 1:131–156, 1997.

    Article  Google Scholar 

  11. Blum, A.L., and Langley, P., Selection of relevant features and examples in machine learning. Artif. Intell. 97:245–271, 1997.

    Article  Google Scholar 

  12. Pattaraintakorn, P., Cercone, N., and Naruedomkul, K., Rule learning: ordinal prediction based on rough sets and soft-computing. Appl. Math. Lett. 19:1300–1307, 2006. doi:10.1016/j.aml.2005.08.004.

    Article  Google Scholar 

  13. Pappu, V., Panagopoulos, O.P., Xanthopoulos, P., and Pardalos, P.M., Sparse proximal support vector machines for feature selection in high dimensional datasets. Expert Systems with Applications. 42:9183–9191, 2015.

    Article  Google Scholar 

  14. Cao, B., Shen, D., Sun, J.T., Yang, Q., and Chen, Z., Feature selection in a kernel space. Proceedings of the 24th international conference on. Mach. Learn. 121–128, 2007. doi:10.1145/1273496.1273512.

  15. Zhou, Q., Zhou, H., and Li, T., Cost-sensitive feature selection using random forest: selecting low-cost subsets of informative features. Knowl.-Based Syst. 95:1–11, 2015. doi:10.1016/j.knosys.2015.11.010.

    Article  Google Scholar 

  16. Prasad M, Sowmya A, Koch I (2004) Efficient feature selection based on independent component analysis. Intelligent Sensors, Sensor Networks and Information Processing Conference. 427–432. doi:10.1109/ISSNIP.2004.1417499

  17. Lu, C., Zhu, Z., and Gu, X., An intelligent system for lung cancer diagnosis using a new genetic algorithm based feature selection method. J. Med. Syst. 38:1–9, 2014. doi:10.1007/s10916–014-0097-y.

    Article  CAS  Google Scholar 

  18. Ozcift, A., and Gulten, A., A robust multi-class feature selection strategy based on rotation forest ensemble algorithm for diagnosis of erythemato-squamous diseases. J. Med. Syst. 36:941–949, 2012. doi:10.1007/s10916–010–9558-0.

    Article  PubMed  Google Scholar 

  19. Nalband, S., Sundar, A., Prince, A.A., and Agarwal, A., Feature selection and classification methodology for the detection of knee-joint disorders. Comput. Methods Prog. Biomed. 127:94–104, 2016. doi:10.1016/j.cmpb.2016.01.020.

    Article  Google Scholar 

  20. Ozcift, A., Enhanced cancer recognition system based on random forests feature elimination algorithm. J. Med. Syst. 36:2577–2585, 2012. doi:10.1007/s10916–011–9730-1.

    Article  PubMed  Google Scholar 

  21. Hannah, I.H., Bagyamathi, M., and Azar, A.T., A novel hybrid feature selection method based on rough set and improved harmony search. Neural Comput. & Applic. 26:1859–1880, 2015. doi:10.1007/s00521–015–1840-0.

    Article  Google Scholar 

  22. Hannah, I.H., Azar, A.T., and Jothi, G., Supervised hybrid feature selection based on PSO and rough sets for medical diagnosis. Comput. Methods Prog. Biomed. 113(1):175–185, 2014. doi:10.1016/j.cmpb.2013.10.007.

    Article  Google Scholar 

  23. Gheyas, I.A., and Smith, L.S., Feature subset selection in large dimensionality domains. Pattern Recogn. 43:5–13, 2010. doi:10.1016/j.patcog.2009.06.009.

    Article  Google Scholar 

  24. Mitra, P., Murthy, C.A., and Pal, S.K., Unsupervised feature selection using feature similarity. IEEE Trans. Pattern Anal. Mach. Intell. 24:301–312, 2002. doi:10.1109/34.990133.

    Article  Google Scholar 

  25. Chandrashekar, G., and Ferat, S., A survey on feature selection methods. Comput. Electr. Eng. 40:16–28, 2014. doi:10.1016/j.compeleceng.2013.11.024.

    Article  Google Scholar 

  26. Wroblewski, J., Finding minimal reducts using genetic algorithms. Second Annual Join Conference on Information Science. 186–189, 1995.

  27. Jensen, R., and Shen, Q., Finding rough set reducts with ant colony optimization. UK workshop on computational intelligence. 1, 2003.

  28. Sengupta, N., Sen, J., Sil, J., and Saha, M., Designing of on line intrusion detection system using rough set theory and Q-learning algorithm. Neurocomputing. 111:161–168, 2013. doi:10.1016/j.neucom.2012.12.023.

    Article  Google Scholar 

  29. Swiniarski, R.W., and Skowron, A., Rough set methods in feature selection and recognition. Pattern Recogn. Lett. 24:833–849, 2003. doi:10.1016/S0167–8655(02)00196–4.

    Article  Google Scholar 

  30. Peters J F, Ramanna S (2008) Feature selection: Near set approach. In: Mining complex data. Springer: Berlin Heidelberg, pp 57–71.

  31. Jensen, R., and Shen, Q., Fuzzy-rough sets assisted attribute selection. IEEE Trans. Fuzzy Syst. 15:73–89, 2007. doi:10.1109/TFUZZ.2006.889761.

    Article  Google Scholar 

  32. Zhang, Z., and Hancock, E.R., Hypergraph based information-theoretic feature selection. Pattern Recogn. Lett. 33:1991–1999, 2012. doi:10.1016/j.patrec.2012.03.021.

    Article  Google Scholar 

  33. Hu X, Cercone N, Han J (1994) An attribute-oriented rough set approach for knowledge discovery in databases. In: Rough sets, fuzzy sets and knowledge discovery. Springer, pp 90–99.

  34. Hu, K., Lu, Y., and Shi, C., Feature ranking in rough sets. AI Commun. 16:41–50, 2003.

    Google Scholar 

  35. Mac Parthaláin, N., and Shen, Q., Exploring the boundary region of tolerance rough sets for feature selection. Pattern Recogn. 42:655–667, 2009. doi:10.1016/j.patcog.2008.08.029.

    Article  Google Scholar 

  36. Slezak, D., Approximate entropy reducts. Fundamenta informaticae. 53:365–390, 2002.

    Google Scholar 

  37. Yan, X.Z., Zuopeng, L., and Ru, W.S., Quick attribute reduction algorithm with complexity of max(O (| C|| U|), O (| C|(2)| U/C|)). Comput. J. 29:391–399, 2006. doi:10.3321/j.issn:0254–4164.2006.03.006.

    Google Scholar 

  38. Eesa, A.S., Orman, Z., and Brifcani, A.M.A., A novel feature-selection approach based on the cuttlefish optimization algorithm for intrusion detection systems. Expert Systems with Applications. 42:2670–2679, 2015. doi:10.1016/j.eswa.2014.11.009.

    Article  Google Scholar 

  39. Lassez J L, Rossi R, Sheel S, Mukkamala S (2008) Signature based intrusion detection using latent semantic analysis. IEEE International Joint Conference on Neural Networks. 1068–1074. doi:10.1109/IJCNN.2008.4633931

  40. Nguyen H, Franke K, Petrović S (2010) Improving effectiveness of intrusion detection by correlation feature selection. ARES’10 International Conference on Availability, Reliability, and Security. 17–24. doi:10.1109/ARES.2010.70

  41. Bakar, A.A., Sulaiman, M.N., Othman, M., and Selamat, M., H (200) Finding minimal reduct with binary integer programming in data mining. Proceedings TENCON. 3:141–146, 2000. doi:10.1109/TENCON.2000.892239.

    Google Scholar 

  42. Wang, X., Yang, J., Teng, X., Xia, W., and Jensen, R., Feature selection based on rough sets and particle swarm optimization. Pattern Recogn. Lett. 28:459–471, 2007. doi:10.1016/j.patrec.2006.09.003.

    Article  CAS  Google Scholar 

  43. Jiang, F., Sui, Y., and Zhou, L., A relative decision entropy-based feature selection approach. Pattern Recogn. 48:2151–2163, 2015. doi:10.1016/j.patcog.2015.01.023.

    Article  Google Scholar 

  44. Inbarani, H.H., Bagyamathi, M., and Azar, A.T., A novel hybrid feature selection method based on rough set and improved harmony search. Neural Comput. & Applic. 26:1859–1880, 2015. doi:10.1007/s00521–015–1840-0.

    Article  Google Scholar 

  45. Zhang M, Yao J T (2004) A rough sets based approach to feature selection. In, 2004. IEEE annual meeting of the fuzzy information processing NAFIPS'04. 1: 434–439. doi:10.1109/NAFIPS.2004.1336322

  46. Pawlak, Z., Rough sets. Int. J. Comput. Inform. Sci. 11:341–356, 1982. doi:10.1007/BF01001956.

    Article  Google Scholar 

  47. Pawlak, Z., Rough sets: theoretical aspects of reasoning about data. Springer science and business media, B V, 2012.

    Google Scholar 

  48. Abraham, A., Falc, R., and Bello, R., Rough set theory: a true landmark in data analysis. Springer Verlag: Berlin Heidelberg, 2009.

    Book  Google Scholar 

  49. Deo, N., Graph theory with applications to engineering and computer science. Dover publications: New York, 2016.

    Google Scholar 

  50. Berge, C., Graphs and hypergraphs. North-Holland publishing company, Amsterdam, 1973.

    Google Scholar 

  51. Kannan, K., Kanna, B.R., and Aravindan, C., Root mean square filter for noisy images based on hyper graph model. Image Vis. Comput. 28:1329–1338, 2010. doi:10.1016/j.imavis.2010.01.013.

    Article  Google Scholar 

  52. Bretto A, Gillibert L (2005) Hypergraph-based image representation. In: Graph-based representations in pattern recognition. Springer: Berlin Heidelberg, pp 1–11

  53. Bretto, A., and Cherifi, H., Aboutajdine D (2002) Hypergraph imaging: an overview. Pattern Recogn. 35:651–658, 2002. doi:10.1016/S0031–3203(01)00067-X.

    Article  Google Scholar 

  54. Anaraki, J.R., Eftekhari M (2011) Improving fuzzy-rough quick reduct for feature selection. 19th Iranian conference on electrical engineering. 1–6

  55. UCI Repository (2016), http://archive.ics.uci.edu/ml/. Accessed 22 Jun 2016.

  56. Witten, I.H., and Frank, E., Data Mining: practical machine learning tools and techniques with java implementations. Morgan Kaufmann, San Francisco, 2000.

    Google Scholar 

  57. Wang, G.Y., Yu, H., and Yang, D.C., Decision table reduction based on conditional information entropy. Chinese journal of computers - chinese edition. 25:759–766, 2002.

    Google Scholar 

Download references

Acknowledgments

The first and the fourth author thank the Department of Science and Technology, India for INSPIRE Fellowship (Grant No: DST/INSPIRE Fellowship/2013/963) and Fund for Improvement of S&T Infrastructure in Universities and Higher Educational Institutions (SR/FST/ETI-349/2013) for their financial support; The second author thanks the Tata Consultancy Services for their financial support; The third author thanks the Department of Science and Technology - Fund for Improvement of S&T Infrastructure in Universities and Higher Educational Institutions Government of India (SR/FST/MSI-107/2015) for their financial support. We would like to express our gratitude towards the unknown potential reviewers who have agreed to review this paper and provided valuable suggestions to improve the quality of the paper.

Author information

Authors and Affiliations

  1. Centre for Information Super Highway (CISH), School of Computing, SASTRA University, Thanjavur, Tamil Nadu, India

    Nivethitha Somu, M. R. Gauthama Raman & V. S. Shankar Sriram

  2. Department of Mathematics, SASTRA University, Thanjavur, Tamil Nadu, India

    Kannan Kirthivasan

Authors
  1. Nivethitha Somu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. R. Gauthama Raman
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kannan Kirthivasan
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. V. S. Shankar Sriram
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. S. Shankar Sriram.

Additional information

This article is part of the Topical Collection on Systems-Level Quality Improvement

Highlights

• This paper presents a novel Rough Set based K – Helly Property (RSKHT) feature selection technique to identify the predominant features in multidimensional medical datasets.

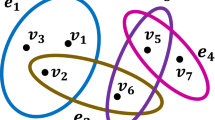
• RSKHT uses Rough Set Theory (RST) to obtain the possible reducts and K – Helly property of hypergraph to reveal the n – ary relations among the feature sets in the early stage of data representation.

• Optimal feature subset obtained from the RSKHT had been validated based on the reduct size, classifier’s accuracy and time complexity.

• The complexity of RSKHT technique had been reduced by the exploitation of the K – Helly property of the hypergraph.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Somu, N., Raman, M.R.G., Kirthivasan, K. et al. Hypergraph Based Feature Selection Technique for Medical Diagnosis. J Med Syst 40, 239 (2016). https://doi.org/10.1007/s10916-016-0600-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10916-016-0600-8

Keywords

Search

Navigation