iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://unpaywall.org/10.1007/S10623-023-01308-3
Permutation polynomials and their compositional inverses over finite fields by a local method | Designs, Codes and Cryptography Skip to main content
Springer Nature Link
Log in

Permutation polynomials and their compositional inverses over finite fields by a local method

  • Published:
Designs, Codes and Cryptography Aims and scope Submit manuscript

Abstract

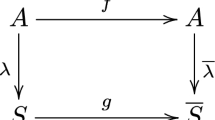
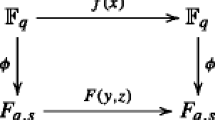
Recently, P. Yuan presented a local method to find permutation polynomials and their compositional inverses over finite fields. The work of P. Yuan inspires us to construct some classes of permutation polynomials and their compositional inverses by the local method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Akbary A., Ghioca D., Wang Q.: On constructing permutations of finite fields. Finite Fields Their Appl. 17(1), 51–67 (2011).

    Article  MathSciNet  Google Scholar 

  2. Cepak N., Charpin P., Pasalic E.: Permutations via linear translators. Finite Fields Their Appl. 45, 19–42 (2017).

    Article  MathSciNet  Google Scholar 

  3. Coulter R.S., Henderson M.: The compositional inverse of a class of permutation polynomials over a finite field. Bull. Aust. Math. Soc. 65(3), 521–526 (2002).

    Article  MathSciNet  Google Scholar 

  4. Ding C.: Cyclic codes from some monomials and trinomials. SIAM J. Discret. Math. 27(4), 1977–1994 (2013).

    Article  MathSciNet  Google Scholar 

  5. Ding C., Yuan J.: A family of skew Hadamard difference sets. J. Comb. Theory A 113(7), 1526–1535 (2006).

    Article  MathSciNet  Google Scholar 

  6. Ding C., Zhou Z.: Binary cyclic codes from explicit polynomials over \(GF (2m)\). Discret. Math. 321, 76–89 (2014).

    Article  Google Scholar 

  7. Gupta R., Gahlyan P., Sharma R.: New classes of permutation trinomials over \({\mathbb{F} }_{q^3}\). Finite Fields Their Appl. 84, 102110 (2022).

    Article  Google Scholar 

  8. Laigle-Chapuy Y.: Permutation polynomials and applications to coding theory. Finite Fields Their Appl. 13(1), 58–70 (2007).

    Article  MathSciNet  Google Scholar 

  9. Li K., Qu L., Chen X.: New classes of permutation binomials and permutation trinomials over finite fields. Finite Fields Their Appl. 43, 69–85 (2017).

    Article  MathSciNet  CAS  Google Scholar 

  10. Li K., Qu L., Wang Q.: Compositional inverses of permutation polynomials of the form \(x^rh(x^s)\) over finite fields. Cryptogr. Commun. 11, 279–298 (2019).

    Article  MathSciNet  Google Scholar 

  11. Lidl R., Niederreiter H.: Introduction to finite fields and their applications. Cambridge University Press, New York (1994).

    Book  Google Scholar 

  12. Lidl R., Niederreiter H.: Finite fields, vol. 20. Cambridge University Press, New York (1997).

    Google Scholar 

  13. Niu T., Li K., Qu L., Wang Q.: Finding compositional inverses of permutations from the AGW criterion. IEEE Trans. Inf. Theory 67(8), 4975–4985 (2021).

    Article  MathSciNet  Google Scholar 

  14. Rivest R.L., Shamir A., Adleman L.: A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 21(2), 120–126 (1978).

    Article  MathSciNet  Google Scholar 

  15. Schwenk J., Huber K.: Public key encryption and digital signatures based on permutation polynomials. Electron. Lett. 34(8), 759–760 (1998).

    Article  ADS  Google Scholar 

  16. Tu Z., Zeng X.: Two classes of permutation trinomials with Niho exponents. Finite Fields Their Appl. 53, 99–112 (2018).

    Article  MathSciNet  Google Scholar 

  17. Tuxanidy A., Wang Q.: On the inverses of some classes of permutations of finite fields. Finite Fields Their Appl. 28, 244–281 (2014).

    Article  MathSciNet  Google Scholar 

  18. Tuxanidy A., Wang Q.: Compositional inverses and complete mappings over finite fields. Discret. Appl. Math. 217, 318–329 (2017).

    Article  MathSciNet  Google Scholar 

  19. Wang Q.: A note on inverses of cyclotomic mapping permutation polynomials over finite fields. Finite Fields Their Appl. 45, 422–427 (2017).

    Article  ADS  MathSciNet  CAS  Google Scholar 

  20. Wu B.: The compositional inverse of a class of linearized permutation polynomials over \({\mathbb{F} }_{2^n}\), \(n\) odd. Finite Fields Their Appl. 29, 34–48 (2014).

    Article  MathSciNet  CAS  Google Scholar 

  21. Wu B., Liu Z.: Linearized polynomials over finite fields revisited. Finite Fields Their Appl. 22, 79–100 (2013).

    Article  MathSciNet  Google Scholar 

  22. Wu B., Liu Z.: The compositional inverse of a class of bilinear permutation polynomials over finite fields of characteristic 2. Finite Fields Their Appl. 24, 136–147 (2013).

    Article  MathSciNet  Google Scholar 

  23. Wu D., Yuan P.: Further results on permutation polynomials from trace functions. Appl. Algebra Eng. Commun. Comput. 33(4), 341–351 (2022).

    Article  MathSciNet  Google Scholar 

  24. Wu D., Yuan P.: Some classes of permutation polynomials of the form \(b(x^q+ax+\delta )^{i(q^2-1)/d+1}+c(x^q+ax+\delta )^{j(q^2-1)/d+1}+{L}(x)\) over \({\mathbb{F} }_{q^2}\). Appl. Algebra Eng. Commun. Comput. 33(2), 135–149 (2022).

    Article  Google Scholar 

  25. Xu G., Luo G., Cao X.: Several classes of permutation polynomials of the form \((x^{p^m}- x+ \delta )^s+ x \) over \({\mathbb{F} }_{p^{2m}}\). Finite Fields Their Appl. 79, 102001 (2022).

    Article  Google Scholar 

  26. Yuan P.: Compositional inverses of AGW-PPs (2022). arXiv preprint arXiv:2203.00279

  27. Yuan P.: Local method for compositional inverses of permutational polynomials (2022). arXiv preprint arXiv:2211.10083

  28. Yuan P., Ding C.: Permutation polynomials over finite fields from a powerful lemma. Finite Fields Their Appl. 17(6), 560–574 (2011).

    Article  MathSciNet  Google Scholar 

  29. Yuan P., Zheng Y.: Permutation polynomials from piecewise functions. Finite Fields Their Appl. 35, 215–230 (2015).

    Article  MathSciNet  Google Scholar 

  30. Zeng X., Zhu X., Li N., Liu X.: Permutation polynomials over \({\mathbb{F} }_{2^n}\) of the form \((x^{2^i}+ x+ \delta )^{s_1}+ (x^{2^i}+ x+ \delta )^{s_2}+ x\). Finite Fields Their Appl. 47, 256–268 (2017).

    Article  MathSciNet  Google Scholar 

  31. Zheng Y., Yuan P., Pei D.: Large classes of permutation polynomials over \({\mathbb{F} }_{q^2}\). Des. Codes Cryptogr. 81, 505–521 (2016).

    Article  MathSciNet  Google Scholar 

  32. Zheng Y., Wang Q., Wei W.: On inverses of permutation polynomials of small degree over finite fields. IEEE Trans. Inf. Theory 66(2), 914–922 (2019).

    Article  MathSciNet  Google Scholar 

  33. Zheng D., Yuan M., Li N., Hu L., Zeng X.: Constructions of involutions over finite fields. IEEE Trans. Inf. Theory 65(12), 7876–7883 (2019).

    Article  MathSciNet  Google Scholar 

  34. Zheng D., Yuan M., Yu L.: Two types of permutation polynomials with special forms. Finite Fields Their Appl. 56, 1–16 (2019).

    Article  MathSciNet  Google Scholar 

Download references

Funding

The research of Pingzhi Yuan is partially supported by the National Natural Science Foundation of China (Grant No. 12171163). The research of Danyao Wu is partially supported by the Guangdong Basic and Applied Basic Research Foundation (Grant No. 2020A1515111090).

Author information

Authors and Affiliations

  1. School of Computer Science and Technology, Dongguan University of Technology, Dongguan, 523808, China

    Danyao Wu

  2. School of Mathematics, South China Normal University, Guangzhou, 510631, China

    Pingzhi Yuan

Authors
  1. Danyao Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pingzhi Yuan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Danyao Wu.

Additional information

Communicated by P. Charpin.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, D., Yuan, P. Permutation polynomials and their compositional inverses over finite fields by a local method. Des. Codes Cryptogr. 92, 267–276 (2024). https://doi.org/10.1007/s10623-023-01308-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10623-023-01308-3

Keywords

Mathematics Subject Classification

Search

Navigation