iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://unpaywall.org/10.1007/S10623-009-9345-4
A tight asymptotic bound on the size of constant-weight conflict-avoiding codes | Designs, Codes and Cryptography Skip to main content
Springer Nature Link
Log in

A tight asymptotic bound on the size of constant-weight conflict-avoiding codes

  • Published:
Designs, Codes and Cryptography Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

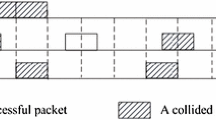
In the study of multiple-access in the collision channel, conflict-avoiding code is used to guarantee that each transmitting user can send at least one packet successfully in the worst case within a fixed period of time, provided that at most k users out of M potential users are active simultaneously. The number of codewords in a conflict-avoiding code determines the number of potential users that can be supported in a system. Previously, upper bound on the size of conflict-avoiding code is known only for Hamming weights three, four and five. The asymptotic upper in this paper extends the known results to all Hamming weights, and is proved to be tight by exhibiting infinite sequences of conflict-avoiding codes which meet this bound asymptotically for all Hamming weights.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Chen C.S., Wong W.S., Song Y.Q. (2008) Constructions of robust protocol sequences for wireless sensor and ad hoc networks. IEEE Trans. Veh. Tech. 57(5): 3053–3063

    Article  Google Scholar 

  2. da Rocha V.C. Jr. (2000) Protocol sequences for collision channel without feedback. IEE Electron. Lett. 36(24): 2010–2012

    Article  Google Scholar 

  3. Györfi L., Vajda I. (1993) Construction of protocol sequences for multiple-access collision channel without feedback. IEEE Trans. Inform. Theory 39(5): 1762–1765

    Article  MATH  Google Scholar 

  4. Hardy G.H. (1999) Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd edn. Chelsea, New York

    Google Scholar 

  5. Hecke E. (1981) Lectures on the Theory of Algebraic Numbers. No. 77 in Graduate Texts in Math. Springer-Verlag, New York

    Google Scholar 

  6. Ireland K., Rosen M. (1990) A Classical Introduction to Modern Number Theory. Springer-Verlag, New York

    MATH  Google Scholar 

  7. Jimbo M., Mishima M., Janiszewski S., Teymorian A.Y., Tonchev V.D. (2007) On conflict-avoiding codes of length n = 4m for three active users. IEEE Trans. Inform. Theory 53(8): 2732–2742

    Article  MathSciNet  Google Scholar 

  8. Kneser M. (1953) Abschätzungen der asymptotischen dichte von summenmengen. Math. Zeit. 58: 459–484

    Article  MATH  MathSciNet  Google Scholar 

  9. Levenshtein V.I.: Conflict-avoiding codes with multiple active users. In: Proc. 14th Int. Conf. on Probl. Theor. Cybern., Moscow (2005), p. 86.

  10. Levenshtein V.I. (2007) Conflict-avoiding codes for three active users and cyclic triple systems. Probl. Inform. Transm. 43(3): 199–212

    Article  MATH  MathSciNet  Google Scholar 

  11. Levenshtein V.I., Han Vinck A.J. (1993) Perfect (d,k)-codes capable of correcting single peak-shift. IEEE Trans. Inform. Theory 39(2): 656–662

    Article  MATH  MathSciNet  Google Scholar 

  12. Mann H.B. (1965) Addition Theorems: The Addition Theorems of Group Theory and Number Theory. No. 18 in Interscience Tracks in Pure and Appl. Math. Interscience Publisher, New York

    Google Scholar 

  13. Massey J.L., Mathys P. (1985) The collision channel without feedback. IEEE Trans. Inform. Theory 31(2): 192–204

    Article  MATH  MathSciNet  Google Scholar 

  14. Mathys P. (1990) A class of codes for a T-active-users-out-of-N multiple-access communication system. IEEE Trans. Inform. Theory 36(6): 1206–1219

    Article  MATH  MathSciNet  Google Scholar 

  15. Mishima M., Fu H.L., Uruno S. (2009) Optimal conflict-avoiding codes of length n ≡ 0 (mod 16) and weight 3. Des. Codes Cryptogr. 52(3): 275–291

    Article  MATH  MathSciNet  Google Scholar 

  16. Momihara K. (2007) Necessary and sufficient conditions for tight equi-difference conflict-avoiding codes of weight three. Des. Codes Cryptogr. 45: 379–390

    Article  MATH  MathSciNet  Google Scholar 

  17. Momihara K. (2009) On cyclic 2(k − 1)-support (n, k)k-1 difference fmilies. Finite Fields Appl. 15: 415–427

    Article  MATH  MathSciNet  Google Scholar 

  18. Momihara K., Müller M., Satoh J., Jimbo M. (2007) Constant weight conflict-avoiding codes. SIAM J. Discrete Math. 21(4): 959–979

    Article  MATH  MathSciNet  Google Scholar 

  19. Nathanson M.B. (1996) Additive Number Theory—Inverse Problems and Geometry of Sumsets. No. 165 in Graduate Texts in Math. Springer-Verlag, New York

    Google Scholar 

  20. A N.Q., Györfi L., Massey J.L. (1992) Constructions of binary constant-weight cyclic codes and cyclically permutable codes. IEEE Trans. Inform. Theory 38(3): 940–949

    Article  MATH  MathSciNet  Google Scholar 

  21. Rudin W.: Principles of Mathematical Analysis. McGraw Hill (1976).

  22. Tonchev V.D.: Tables of conflict-avoiding codes (2005). Avaiable online at http://www.math.mtu.edu/~tonchev/CAC.html.

  23. Wong W.S. (2007) New protocol sequences for random access channels without feedback. IEEE Trans. Inform. Theory 53(6): 2060–2071

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Information Engineering, The Chinese University of Hong Kong, Shatin, Hong Kong

    Kenneth W. Shum & Wing Shing Wong

Authors
  1. Kenneth W. Shum
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wing Shing Wong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kenneth W. Shum.

Additional information

Communicated by V. D. Tonchev.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Shum, K.W., Wong, W.S. A tight asymptotic bound on the size of constant-weight conflict-avoiding codes. Des. Codes Cryptogr. 57, 1–14 (2010). https://doi.org/10.1007/s10623-009-9345-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10623-009-9345-4

Keywords

Mathematics Subject Classification (2000)

Search

Navigation