Quasi Right Factorization Structures as Presheaves

Abstract

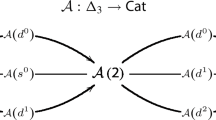
In this article the notion of quasi right factorization structure in a category $\cal{X}$ is given. The main result is a one to one correspondence between certain classes of quasi right factorization structures and 2-reflective subobjects of a predefined object in $\bf{\it{L}}\it{ax}({\it{PrOrd}}^{\bf{\cal{X}}^{op}})$. Also a characterization of quasi right factorization structures in terms of images is given. As an application, the closure operators are discussed and it is shown that quasi closed members of certain collections are quasi right factorization structures. Finally several examples are furnished.