Abstract
We present a framework for statically detecting deadlocks in a concurrent object-oriented language with asynchronous method calls and cooperative scheduling of method activations. Since this language features recursion and dynamic resource creation, deadlock detection is extremely complex and state-of-the-art solutions either give imprecise answers or do not scale. In order to augment precision and scalability, we propose a modular framework that allows several techniques to be combined. The basic component of the framework is a front-end inference algorithm that extracts abstract behavioral descriptions of methods, called contracts, which retain resource dependency information. This component is integrated with a number of possible different back-ends that analyze contracts and derive deadlock information. As a proof-of-concept, we discuss two such back-ends: (1) an evaluator that computes a fixpoint semantics and (2) an evaluator using abstract model checking.






















Similar content being viewed by others
Notes
It is worth to recall that, in core ABS, the creation of an object, either with a new or with a new cog, amounts to executing the method init of the corresponding class, whenever defined (the new performs a synchronous invocation, the new cog performs an asynchronous one). In turn, the termination of init triggers the execution of the method run, if present. The method run is asynchronously invoked when init is absent. Since init may be regarded as a method in core ABS, the inference system in our tool explicitly introduces a synchronous invocation to init in case of new and an asynchronous one in case of new cog. However, for simplicity, we overlook this (simple) issue in the rules (T-New) and (T-NewCog), acting as if init and run are always absent.
It is possible to define sufficient conditions on core ABS programs that entail linear recursive contract class tables. For example, two such conditions are that, in (mutual) recursive methods, recursive invocations are either (1) synchronous or (2) asynchronous followed by a get or await synchronization on the future value, without any other get or await synchronization or synchronous invocation in between.
The interested reader may find in [18] the technical reason for unfolding recursive methods as many times as twice the length of the order of the corresponding mutation.
In [18], we have defined a source-to-source transformation taking nonlinear recursive contract class tables and returning linear recursive ones. This transformation introduces fake cog dependencies that returns a false positive when applying DF4ABS/model-check on the example above.
The pi-calculus factorial program is
*factorial?(n,(r,s)).
if n=0 then r?m. s!m else new t in
(r?m. t!(m*n)) | factorial!(n-1,(t,s)) In this code, factorial returns the value (on the channel s) by delegating this task to the recursive invocation, if any. In particular, the initial invocation of factorial, which is r!1 | factorial!(n,(r,s)), performs a synchronization between r!1 and the input r?m in the continuation of factorial?(n,(r,s)). In turn, this may delegate the computation of the factorial to a subsequent synchronization on a new channel t. TyPiCal signals a deadlock on the two inputs r?m because it fails in connecting the output t!(m*n) with them.
References
Abadi, M., Flanagan, C., Freund, S.N.: Types for safe locking: static race detection for java. ACM Trans. Program. Lang. Syst. 28, 207–255 (2006)
Boyapati, C., Lee, R., Rinard, M.: Ownership types for safe program: preventing data races and deadlocks. In: Proceedings of OOPSLA ’02, pp. 211–230. ACM, London (2002)
Carlsson, R., Millroth, H.: On cyclic process dependencies and the verification of absence of deadlocks in reactive systems (1997)
Caromel, D.: Towards a method of object-oriented concurrent programming. Commun. ACM 36(9), 90–102 (1993)
Caromel, D., Henrio, L., Serpette, B.P.: Asynchronous and deterministic objects. In: Proceedings of POPL’04, pp. 123–134. ACM, London (2004)
Comtet, L.: Advanced Combinatorics: The Art of Finite and Infinite Expansions. Reidel, Dordrecht (1974)
Coppo, M.: Type inference with recursive type equations. In: Proceedings of FoSSaCS, LNCS, vol. 2030, pp. 184–198. Springer, Berlin (2001)
de Boer, F., Bravetti, M., Grabe, I., Lee, M., Steffen, M., Zavattaro, G.: A petri net based analysis of deadlocks for active objects and futures. In: Proceedings of Formal Aspects of Component Software—9th International Workshop, FACS 2012, Lecture Notes in Computer Science, vol. 7684, pp. 110–127. Springer, Berlin (2012)
de Boer, F., Clarke, D., Johnsen, E.: A complete guide to the future. In: Programming Language and Systems, LNCS, vol. 4421, pp. 316–330. Springer, Berlin (2007)
Flanagan, C., Leino, K.R.M., Lillibridge, M., Nelson, G., Saxe, J.B., Stata, R.: Extended static checking for java. SIGPLAN Not. 37(5), 234–245 (2002)
Flanagan, C., Qadeer, S.: A type and effect system for atomicity. In: PLDI 03: Programming Language Design and Implementation, pp. 338–349. ACM, London (2003)
Flores-Montoya, A., Albert, E., Genaim, S.: May-happen-in-parallel based deadlock analysis for concurrent objects. In: Proceedings of FORTE/FMOODS 2013, Lecture Notes in Computer Science, vol. 7892, pp. 273–288. Springer, Berlin (2013)
Gay, S., Hole, M.: Subtyping for session types in the \(\pi \)-calculus. Acta Inf. 42(2–3), 191–225 (2005)
Giachino, E., Grazia, C.A., Laneve, C., Lienhardt, M., Wong, P.Y.H.: Deadlock analysis of concurrent objects: theory and practice. In: iFM’13, LNCS, vol. 7940, pp. 394–411. Springer, Berlin (2013)
Giachino, E., Kobayashi, N., Laneve, C.: Deadlock detection of unbounded process networks. In: Proceedings of CONCUR 2014, LNCS, vol. 8704, pp. 63–77. Springer, Berlin (2014)
Giachino, E., Laneve, C.: Analysis of deadlocks in object groups. In: FMOODS/FORTE, Lecture Notes in Computer Science, vol. 6722, pp. 168–182. Springer, Berlin (2011)
Giachino, E., Laneve, C.: A beginner’s guide to the deadLock Analysis Model. In: Trustworthy Global Computing—7th International Symposium, TGC 2012, Revised Selected Papers, Lecture Notes in Computer Science, vol. 8191, pp. 49–63. Springer, Berlin (2013)
Giachino, E., Laneve, C.: Deadlock detection in linear recursive programs. In: Proceedings of SFM-14:ESM, LNCS, vol. 8483, pp. 26–64. Springer, Berlin (2014)
Giachino, E., Lascu, T.A.: Lock analysis for an asynchronous object calculus. In: Proceedings of 13th ICTCS (2012)
Henglein, F.: Type inference with polymorphic recursion. ACM Trans. Program. Lang. Syst. 15(2), 253–289 (1993)
Igarashi, A., Kobayashi, N.: A generic type system for the pi-calculus. Theor. Comput. Sci. 311(1–3), 121–163 (2004)
Johnsen, E.B., Hähnle, R., Schäfer, J., Schlatte, R., Steffen, M.: ABS: A core language for abstract behavioral specification. In: Aichernig, B., de Boer, F.S., Bonsangue, M.M. (eds.) Proceedings of 9th International Symposium on Formal Methods for Components and Objects (FMCO 2010), LNCS, vol. 6957, pp. 142–164. Springer, Berlin (2011)
Johnsen, E.B., Owe, O.: An asynchronous communication model for distributed concurrent objects. Softw. Syst. Model. 6(1), 39–58 (2007)
Kerfoot, E., McKeever, S., Torshizi, F.: Deadlock freedom through object ownership. In: T. Wrigstad (ed.) 5rd International Workshop on Aliasing, Confinement and Ownership in object-oriented programming (IWACO), in conjunction with ECOOP 2009 (2009)
Kobayashi, N.: A partially deadlock-free typed process calculus. TOPLAS 20(2), 436–482 (1998)
Kobayashi, N.: A new type system for deadlock-free processes. In: Proceedings of CONCUR 2006, LNCS, vol. 4137, pp. 233–247. Springer, Berlin (2006)
Kobayashi, N.: TyPiCal (2007). http://www.kb.ecei.tohoku.ac.jp/~koba/typical/
Laneve, C., Padovani, L.: The must preorder revisited. In: Proceedings of CONCUR 2007, LNCS, vol. 4703, pp. 212–225. Springer, Berlin (2007)
Milner, R.: A Calculus of Communicating Systems. Springer, Berlin (1982)
Milner, R., Parrow, J., Walker, D.: A calculus of mobile processes, ii. Inf. Comput. 100, 41–77 (1992)
Naik, M., Park, C.S., Sen, K., Gay, D.: Effective static deadlock detection. In: IEEE 31st International Conference on Software Engineering, 2009. ICSE 2009, pp. 386–396 (2009)
Pun, K.I.: behavioural static analysis for deadlock detection. Ph.D. thesis, Faculty olf Mathematics and Natural Sciences, University of Oslo, Norway (2013)
Puntigam, F., Peter, C.: Types for active objects with static deadlock prevention. Fundam. Inf. 48(4), 315–341 (2001)
Requirement elicitation (2009). Deliverable 5.1 of project FP7-231620 (HATS). http://www.hats-project.eu/sites/default/files/Deliverable51_rev2.pdf
Tarjan, R.E.: Depth-first search and linear graph algorithms. SIAM J. Comput. 1(2), 146–160 (1972)
Vasconcelos, V.T., Martins, F., Cogumbreiro, T.: Type inference for deadlock detection in a multithreaded polymorphic typed assembly language. In: Proceedings of PLACES’09, EPTCS, vol. 17, pp. 95–109 (2009)
Visser, W., Havelund, K., Brat, G., Park, S., Lerda, F.: Model checking programs. Autom. Softw. Eng. 10(2), 203–232 (2003)
West, S., Nanz, S., Meyer, B.: A modular scheme for deadlock prevention in an object-oriented programming model. In: ICFEM, pp. 597–612 (2010)
Wong, P.Y.H., Albert, E., Muschevici, R., Proença, J., Schäfer, J., Schlatte, R.: The ABS tool suite: modelling, executing and analysing distributed adaptable object-oriented systems. J. Softw. Tools Technol. Transf. 14(5), 567–588 (2012)
Yonezawa, A., Briot, J.P., Shibayama, E.: Object-oriented concurrent programming in ABCL/1. In: Proceedings of OOPSLA’86, pp. 258–268 (1986)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Prof. Einar Broch Johnsen and Luigia Petre.
Partly funded by the EU Project FP7-610582 ENVISAGE: Engineering Virtualized Services.
Appendices
Appendix 1: Properties of Sect. 4
The initial configuration of a well-typed core ABS program is
where the activity \(\{ [\text {destiny} \mapsto f_{ start}, \bar{x} \mapsto \bot ] \, | \, s \}\) corresponds to the activation of the main function. A computation is a sequence of reductions starting at the initial configuration according to the operational semantics. We show in this appendix that such computations keep configurations well-typed; in particular, we show that the sequence of contracts corresponding to the configurations of the computations is in the later-stage relationship (see Fig. 27).
1.1 Runtime contracts
In order to type the configurations, we use a runtime type system. To this aim we extend the syntax of contracts in Fig. 8 and define extended futures \(F\), extended contracts that, with an abuse of notation, we still denote \({\mathbb {c}}\,\hbox {and}\) runtime contracts \({\mathbb {k}}\) as follows:

As regards \(F\), they are introduced for distinguishing two kind of future names: (1) \(f\) that has been used in the contract inference system as a static time representation of a future, but is now used as its runtime representation; (2)  now replacing \(f\) in its role of static time future (it is typically used to reference a future that is not created yet).
now replacing \(f\) in its role of static time future (it is typically used to reference a future that is not created yet).
As regards  and \({\mathbb {k}}\), the extensions are motivated by the fact that, at runtime, the information about contracts is scattered in all the configuration. However, when we plug all the parts to type the whole configuration, we can merge the different information to get a runtime contract \({\mathbb {k}}'\) such that every contract \({\mathbb {c}}\in {\mathbb {k}}'\) does not contain any reference to futures anymore. This merging is done using a set of rewriting rules \(\Rightarrow \) defined in Fig. 23 that let one replace the occurrences of runtime futures in runtime contracts \({\mathbb {k}}\) with the corresponding contract of the future. We write \(f \in \textit{names}({\mathbb {k}})\) whenever \(f\) occurs in \({\mathbb {k}}\) not as an index. The substitution
and \({\mathbb {k}}\), the extensions are motivated by the fact that, at runtime, the information about contracts is scattered in all the configuration. However, when we plug all the parts to type the whole configuration, we can merge the different information to get a runtime contract \({\mathbb {k}}'\) such that every contract \({\mathbb {c}}\in {\mathbb {k}}'\) does not contain any reference to futures anymore. This merging is done using a set of rewriting rules \(\Rightarrow \) defined in Fig. 23 that let one replace the occurrences of runtime futures in runtime contracts \({\mathbb {k}}\) with the corresponding contract of the future. We write \(f \in \textit{names}({\mathbb {k}})\) whenever \(f\) occurs in \({\mathbb {k}}\) not as an index. The substitution  replaces the occurrences of \(f\) in contracts \({\mathbb {c}}''\) of \({\mathbb {k}}\) (by definition of our configurations, in these cases, \(f\) can never occur as index in \({\mathbb {k}}\)). It is easy to demonstrate that the merging process always terminates and is confluent for non-recursive contracts, and in the following, we let
replaces the occurrences of \(f\) in contracts \({\mathbb {c}}''\) of \({\mathbb {k}}\) (by definition of our configurations, in these cases, \(f\) can never occur as index in \({\mathbb {k}}\)). It is easy to demonstrate that the merging process always terminates and is confluent for non-recursive contracts, and in the following, we let  be the normal form of \({\mathbb {k}}\) with respect to \(\Rightarrow \):
be the normal form of \({\mathbb {k}}\) with respect to \(\Rightarrow \):
Definition 11
A runtime contract \({\mathbb {k}}\) is non-recursive if:
-
all futures \(f\in \textit{names}({\mathbb {k}})\) are declared once in \({\mathbb {k}}\)
-
all futures \(f\in \textit{names}({\mathbb {k}})\) are not recursive, i.e., for all \(\langle {{\mathbb {c}}},{{\mathbb {c}}'}\rangle ^{c}_{f}\in {\mathbb {k}}\), we have \(f\not \in \textit{names}(\langle {{\mathbb {c}}},{{\mathbb {c}}'}\rangle ^{c}_{f})\)
1.2 Typing runtime configurations
The typing rules for the runtime configuration are given in Figs. 24, 25 and 26. Except for few rules (in particular, those in Fig. 24 which type the runtime objects of a configuration), all the typing rules have a corresponding one in the contract inference system defined in Sect. 4. Additionally, the typing judgments are identical to the corresponding one in the inference system, with three minor differences:
-
(i)
The typing environment, which now contains a reference to the contract class table and mappings object names to pairs \(({\mathtt{C}},\mathbb {r})\), is called \({\varDelta }\);
-
(ii)
the typing rules do not collect constraints;
-
(iii)
the \({ rt\_unsync}(\cdot )\) function on environments \({\varDelta }\) is similar to \({ unsync}(\cdot )\) in Sect. 4, except that it now grabs all
 and all futures \(f'\) that was created by the current thread \(f\). More precisely, $$\begin{aligned} \begin{array}{rl} { rt\_unsync}({\varDelta },f) \mathop {=}\limits ^{ def}&{\mathbb {c}}_1 \parallel \cdots \parallel {\mathbb {c}}_n\parallel f_1\parallel \cdots \parallel f_m \end{array} \end{aligned}$$
and all futures \(f'\) that was created by the current thread \(f\). More precisely, $$\begin{aligned} \begin{array}{rl} { rt\_unsync}({\varDelta },f) \mathop {=}\limits ^{ def}&{\mathbb {c}}_1 \parallel \cdots \parallel {\mathbb {c}}_n\parallel f_1\parallel \cdots \parallel f_m \end{array} \end{aligned}$$where
 and \(\{f_1,\dots ,f_m\}=\{f'\;|\;{\varDelta }(f')=(\mathbb {r}',f)\}\).
and \(\{f_1,\dots ,f_m\}=\{f'\;|\;{\varDelta }(f')=(\mathbb {r}',f)\}\).
Finally, few remarks about the auxiliary functions:
-
\(\textit{init}({\mathtt{C}},o)\) is supposed to return the init activity of the class C. However, we have assumed that these activity is always empty, see Footnote 2. Therefore, the corresponding contract will be
 .
. -
\(\textit{atts}({\mathtt{C}},\overline{v}, o, c)\) returns a substitution provided that \(\overline{v}\) have records \(\overline{\mathbb {r}}\) and \(o\) and \(c\) are object and cog identifiers, respectively.
-
\(\textit{bind}(o,f,{\mathtt{m}},\overline{v'},{\mathtt{C}})\) returns the activity corresponding to the method \({\mathtt{C}}.{\mathtt{m}}\) with the parameters \(\overline{v'}\) provided that \(f\) has type \(c \leadsto \mathbb {r}\) and \(\overline{v'}\) have the types \(\overline{\mathbb {r}'}\).
Theorem 3
Let \(P=\bar{I}\ \bar{C}\ \{\overline{T\ x}; s\}\) be a core ABS program and let \({\varGamma } \vdash P \mathrel {:}\textsc {cct},\,\langle {{\mathbb {c}}},{{\mathbb {c}}'}\rangle \, \rhd \, \mathcal {U}\). Let also \(\sigma \) be a substitution satisfying \(\mathcal {U}\) and
Then

where \(l = [\text {destiny} \mapsto f_{ start}, \, \overline{x \mapsto \bot }]\).
Proof
By (TR-Configuration) and (TR-Object) we are reduced to prove:

To this aim, let \(\bar{X}\) be the variables used in the inference rule of (T-Program).
To demonstrate (3) we use (TR-Process). Therefore, we need to prove:
with \({ rt\_unsync}({\varDelta }')=\sigma ({\mathbb {c}}'')\). This proof is done by a standard induction on \(s\), using a derivation tree identical to the one used for the inference (with the minor exception of replacing the \(f\)s used in the inference with corresponding  s). This is omitted because straightforward. \(\square \)
s). This is omitted because straightforward. \(\square \)
Definition 12
A runtime contract \({\mathbb {k}}\) is well formed if it is non- recursive and if futures and method calls in \({\mathbb {k}}\) are placed as described by the typing rules: i.e., in a sequence  , they are present in all \({\mathbb {c}}_i\), \(i_1\le i\le i_k\) with \({\mathbb {c}}_{i_1}\) being when the method is called, and \({\mathbb {c}}_{i_k}\) being when the method is synchronized with. Formally, for all \(\langle {{\mathbb {c}}},{{\mathbb {c}}'}\rangle ^{c}_{f}\in {\mathbb {k}}\), we can derive \(\varnothing \vdash {\mathbb {c}}\mathrel {:}{\mathbb {c}}'\) with the following rules:
, they are present in all \({\mathbb {c}}_i\), \(i_1\le i\le i_k\) with \({\mathbb {c}}_{i_1}\) being when the method is called, and \({\mathbb {c}}_{i_k}\) being when the method is synchronized with. Formally, for all \(\langle {{\mathbb {c}}},{{\mathbb {c}}'}\rangle ^{c}_{f}\in {\mathbb {k}}\), we can derive \(\varnothing \vdash {\mathbb {c}}\mathrel {:}{\mathbb {c}}'\) with the following rules:

Lemma 1
If \({\varDelta }\vdash \textit{cn}\mathrel {:}{\mathbb {k}}\) is a valid statement, then \({\mathbb {k}}\) is well formed.
Proof
The result is given by the way \({ rt\_unsync}(\cdot )\) is used in the typing rules. \(\square \)
In the following theorem, we use the so-called later-stage relation \(\trianglerighteq \) that has been defined in Fig. 27 on runtime contracts.
We observe that the later-stage relation uses a substitution process that also performs a pattern matching operation—therefore, it is partial because the pattern matching may fail. In particular,  (1) extracts the cog names and terms \(\mathbb {s}'\) in \(\mathbb {s}\) that corresponds to occurrences of cog names and record variables in \(\mathbb {r}\) and (2) returns the corresponding substitution.
(1) extracts the cog names and terms \(\mathbb {s}'\) in \(\mathbb {s}\) that corresponds to occurrences of cog names and record variables in \(\mathbb {r}\) and (2) returns the corresponding substitution.
Theorem 4
(Subject reduction) Let \({\varDelta }\vdash _R cn\mathrel {:}{\mathbb {k}}\) and \(cn\rightarrow cn'\). Then, there exist \({\varDelta }'\), \({\mathbb {k}}'\), and an injective renaming of cog names \(\imath \) such that
-
\({\varDelta }' \vdash _R cn'\mathrel {:}{\mathbb {k}}'\) and
-
\(\imath ({\mathbb {k}})\trianglerighteq {\mathbb {k}}'\).
Proof
The proof is a case analysis on the reduction rule used in \(cn\rightarrow cn'\), and we assume that the evaluation of an expression \([\![e]\!]_{\sigma }\) always terminates. We focus on the most interesting cases. We remark that the injective renaming \(\imath \) is used to identify fresh cog names that are created by the static analysis with fresh cog names that are created by the operational semantics. In fact, the renaming is not the identity only in the case of cog creation (second case below).
-
Skip Statement.

By (TR-Object), (TR-Process), (TR-Seq) and (TR-Skip), there exists \({\varDelta }''\) and \({\mathbb {c}}\,\hbox {such}\) that
 . It is easy to see that \({\varDelta }''\vdash _R^{c,o}s\mathrel {:}{\mathbb {c}} \,|\,{\varDelta }''\). Moreover, by (LS-Delete), we have
. It is easy to see that \({\varDelta }''\vdash _R^{c,o}s\mathrel {:}{\mathbb {c}} \,|\,{\varDelta }''\). Moreover, by (LS-Delete), we have  which proves that \({\mathbb {k}}\trianglerighteq {\mathbb {k}}'\).
which proves that \({\mathbb {k}}\trianglerighteq {\mathbb {k}}'\). -
Object creation.

By (TR-Object) and (TR-Process), there exists \({\varDelta }''\) that extends \({\varDelta }\) such that \({\varDelta }''\vdash _R^{c,o}\mathtt{new }\ {\mathtt{C}}(\overline{e})\mathrel {:}\mathbb {r},\,0\mid {\varDelta }''\). Let \({\varDelta }'={\varDelta }[o'\mapsto \mathbb {r}]\). The theorem follows by the assumption that \(p\) is empty (see Footnote 2).
-
Cog creation.

By (TR-Object) and (TR-Process), there exists \({\varDelta }''\) that extends \({\varDelta }\) such that \({\varDelta }''\vdash _R^{c,o}\mathtt{new }\ {\mathtt{C}}(\overline{e})\mathrel {:}[cog:c'',\bar{x:\mathbb {r}}],\,0\mid {\varDelta }''\) for some \(c''\) and records \(\bar{\mathbb {r}}\). Let \({\varDelta }'={\varDelta }[o'\mapsto [cog:c',\bar{x:\mathbb {r}}],c'\mapsto \textit{cog}]\) and \(\imath (c'')=c'\), where \(\imath \) is an injective renaming on cog names. The theorem follows by the assumption that \(p\) is empty (see Footnote 2).
-
Asynchronous calls.

By (TR-Object) and (TR-Process), there exist \(\bar{\mathbb {r}}\), \({\varDelta }_1'\), \({\mathbb {c}}\,\hbox {and}\, {\mathbb {k}}''\) such that (let \(f'=l(\text {destiny})\))
-
\({\mathbb {k}}=\langle {{\mathbb {c}}},{{ rt\_unsync}({\varDelta }_1',f')}\rangle _{\mathtt{cog}(o)}^{f'}{\parallel }{\mathbb {k}}''\)
-
\({\varDelta }\vdash _{R}^{c,o} \bar{v} :\bar{\mathbb {x}}\) (with \(l=[\bar{y \mapsto v}]\))
-
\({\varDelta }\vdash _{R}^{c,o} q :{\mathbb {k}}''\)
-
\({\varDelta }[\bar{y\mapsto \mathbb {r}}]\vdash _R^{c,o} x=e!m(\overline{e});s\mathrel {:}{\mathbb {c}}\mid {\varDelta }_1'\)
Let \({\varDelta }_1={\varDelta }[\bar{y\mapsto \mathbb {r}}]\): by either (TR-Var-Record) or (TR-Field-Record) and (TR-AInvk), there exist \(\mathbb {r}=c' \leadsto \mathbb {r}'\) (where \(c'\) is the cog of the record of \(e\)),
 and
and  such that
such that  . By construction of the type system (in particular, the rules (TR-Get)
\(^{*}\) and (TR-Await)
\(^{*}\)), there exists a term \(t\) such that
. By construction of the type system (in particular, the rules (TR-Get)
\(^{*}\) and (TR-Await)
\(^{*}\)), there exists a term \(t\) such that  and such that
and such that  (with
(with  and \([\checkmark ]=\checkmark \) iff
and \([\checkmark ]=\checkmark \) iff  is checked). By construction of the rt_unsync function, there exist a term \(t'\) such that
is checked). By construction of the rt_unsync function, there exist a term \(t'\) such that  and
and 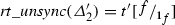 . Finally, if we note \({\varDelta }'\triangleq {\varDelta }[f\mapsto (\mathbb {r},f')]\), we can type the invocation message with
. Finally, if we note \({\varDelta }'\triangleq {\varDelta }[f\mapsto (\mathbb {r},f')]\), we can type the invocation message with  (as \(c'\) is the cog of the record of \(\mathtt{this}\) in \({\mathbb {c}}'\)), we have
(as \(c'\) is the cog of the record of \(\mathtt{this}\) in \({\mathbb {c}}'\)), we have-

-
the rule (LS-AInvk) gives us that

-
-
Method instantiations.

By assumption and rules (TR-Parallel) and (R-Invoc) we have \({\varDelta }(o)=({\mathtt{C}},\mathbb {r})\), \({\varDelta }(f)=(c \leadsto \mathbb {r}',0)\), \(c=\mathtt{cog}(\mathbb {r})\) and \({\mathbb {k}}={[{C!{\mathtt{m}}\ \mathbb {r}(\overline{\mathbb {r}})\rightarrow \mathbb {r}'}]_{f}}\parallel {\mathbb {k}}'\) with \({\varDelta }\vdash _R \textit{invoc}(o,f,m,\overline{v}):{[{{\mathtt{C}}!{\mathtt{m}}~\mathbb {r}(\overline{\mathbb {r}})\rightarrow \mathbb {r}'}]_{f}}\) and \({\varDelta }\vdash _R ob(o,a,p,q):{\mathbb {k}}'\). Let \(\overline{x}\) be the formal parameters of m in \({\mathtt{C}}\). The auxiliary function \(\textit{bind}(o,f,m,\overline{v},{\mathtt{C}})\) returns a process \(\{[\text {destiny}\mapsto f, \overline{x}\mapsto \overline{v}] \; | \; s\}\). It is possible to demonstrate that \({\varDelta }\vdash _R^{c,o} \{l[\text {destiny}\mapsto f, \overline{x}\mapsto \overline{v}]|s\}:\langle {{\mathbb {c}}_{{\mathtt{m}}}},{{\mathbb {c}}'_{{\mathtt{m}}}}\rangle _{c}^{f}\), where
 and
and  and \(\bar{c'}\in \mathbb {s}'{\setminus }(\mathbb {s}\cup \bar{\mathbb {s}})\) with \(\bar{c}\,\mathrm{fresh}\) and
and \(\bar{c'}\in \mathbb {s}'{\setminus }(\mathbb {s}\cup \bar{\mathbb {s}})\) with \(\bar{c}\,\mathrm{fresh}\) and  . By rules (TR-Process) and (TR-Object), it follows that \({\varDelta }\vdash _R ob(o,a,p,q\cup \{\textit{bind}(o,f,m,\overline{v},{\mathtt{C}})\}): {\mathbb {k}}'{\parallel }\langle {{\mathbb {c}}_{{\mathtt{m}}}},{{\mathbb {c}}'_{{\mathtt{m}}}}\rangle _{c}^{f}\). Moreover, by applying the rule (LS-Bind), we have that \({[{{\mathtt{C}}!{\mathtt{m}}~\mathbb {r}(\overline{\mathbb {r}})\rightarrow \mathbb {r}'}]_{f}}\trianglerighteq \langle {{\mathbb {c}}_{{\mathtt{m}}}},{{\mathbb {c}}'_{{\mathtt{m}}}}\rangle _{c}^{f}\) which implies with the rule (LS-Global) that \({\mathbb {k}}\trianglerighteq {\mathbb {k}}'\).
. By rules (TR-Process) and (TR-Object), it follows that \({\varDelta }\vdash _R ob(o,a,p,q\cup \{\textit{bind}(o,f,m,\overline{v},{\mathtt{C}})\}): {\mathbb {k}}'{\parallel }\langle {{\mathbb {c}}_{{\mathtt{m}}}},{{\mathbb {c}}'_{{\mathtt{m}}}}\rangle _{c}^{f}\). Moreover, by applying the rule (LS-Bind), we have that \({[{{\mathtt{C}}!{\mathtt{m}}~\mathbb {r}(\overline{\mathbb {r}})\rightarrow \mathbb {r}'}]_{f}}\trianglerighteq \langle {{\mathbb {c}}_{{\mathtt{m}}}},{{\mathbb {c}}'_{{\mathtt{m}}}}\rangle _{c}^{f}\) which implies with the rule (LS-Global) that \({\mathbb {k}}\trianglerighteq {\mathbb {k}}'\). -
Getting the value of a future.

By assumption and rules (TR-Parallel), (TR-Object) and (TR-Future-Tick), there exists \({\varDelta }''\), \({\mathbb {c}},\,{\mathbb {k}}''\) such that (let \(f'=\) l [destiny])
-
\({\varDelta }\vdash _R^{\mathtt{cog}(o),o}\{l|x=e.\mathtt{get };s\}\mathrel {:} \langle {{\mathbb {c}}},{{ rt\_unsync}({\varDelta }'',f')}\rangle _{\mathtt{cog}(o)}^{f'}\)
-
\({\varDelta }\vdash _R^{\mathtt{cog}(o),o}q\mathrel {:}{\mathbb {k}}''\)
-
\({\varDelta }\vdash _R \textit{fut}(f,v):0\)
-
\({\mathbb {k}}=\langle {{\mathbb {c}}},{{ rt\_unsync}({\varDelta }'',f')}\rangle _{\mathtt{cog}(o)}^{f'}\parallel {\mathbb {k}}''\), and
-
\([\![e]\!]_{a\circ l}=f\).
Moreover, as \(\textit{fut}(f,v)\) is typable and contains a value, we know that
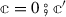 (\(e.\mathtt{get }\) has contract \(0\)). With the rule (TR-Pure), have that \({\varDelta }\vdash _R^{\mathtt{cog}(o),o}\{l|x=v;s\}\mathrel {:}\langle {{\mathbb {c}}},{{ rt\_unsync}({\varDelta }'',f')}\rangle _{\mathtt{cog}(o)}^{f'}\), and with \({\mathbb {k}}'={\mathbb {k}}\), we have the result.
(\(e.\mathtt{get }\) has contract \(0\)). With the rule (TR-Pure), have that \({\varDelta }\vdash _R^{\mathtt{cog}(o),o}\{l|x=v;s\}\mathrel {:}\langle {{\mathbb {c}}},{{ rt\_unsync}({\varDelta }'',f')}\rangle _{\mathtt{cog}(o)}^{f'}\), and with \({\mathbb {k}}'={\mathbb {k}}\), we have the result. -
-
Remote synchronous call. Similar to the cases of asynchronous call with a get-synchronization. The result follows, in particular, from rule (LS-RSInvk) of Fig. 27.
-
Cog-local synchronous call. Similar to case of asynchronous call. The result follows, in particular, from rules (LS-SimpleNull) of Fig. 27 and from the Definition of \({\mathtt{C}}.{\mathtt{m}}\ \mathbb {r}(\bar{\mathbb {r}})\rightarrow \mathbb {s}\).
-
Local Assignment.

By assumption and rules (TR-Object), (TR-Process), (TR-Seq), (TR-Var-Record) and (TR-Pure), there exists \({\varDelta }''\), \({\mathbb {c}},\,{\mathbb {k}}''\) such that (we note \({\varDelta }_1\) for \({\varDelta }[\overline{y:\mathbb {x}}]\) and \(f\) for \(l\) \([\text {destiny}]\))
-

-
\({\varDelta }\vdash _R^{\mathtt{cog}(o),o}q\mathrel {:}{\mathbb {k}}''\)
-
\({\mathbb {k}}=\langle {{\mathbb {c}}},{{ rt\_unsync}({\varDelta }'',f)}\rangle _{\mathtt{cog}(o)}^{f}\parallel {\mathbb {k}}''\), and
-
\([\![e]\!]_{a\circ l}=v\).
We have
$$\begin{aligned} {\varDelta }\vdash _R^{\mathtt{cog}(o),o}\{l[x\mapsto [\![e]\!]_{(a+ l)}]|s\}\mathrel {:} \langle {{\mathbb {c}}},{{ rt\_unsync}({\varDelta }'',f)}\rangle _{\mathtt{cog}(o)}^{f} \end{aligned}$$which gives us the result with \({\mathbb {k}}'=\langle {{\mathbb {c}}},{{ rt\_unsync}({\varDelta }'',f)}\rangle ^{c}_{f}cpar{\mathbb {k}}'\).\(\square \)
-
Appendix 2: Properties of Sect. 5
In this section, we will prove that the statements given in Sect. 5 are correct, i.e., that the fixpoint analysis does detect deadlocks. To prove that statement, we first need to define the dependencies generated by the runtime contract of a running program. Then, our proof works in three steps: (1) First, we show that our analysis (performed at static time) contains all the dependencies of the runtime contract of the program; (2) second, the dependencies in a program at runtime are contained in the dependencies of its runtime contract; and (3) finally, when \(\textit{cn}\) (typed with \({\mathbb {k}}\)) reduces to \(\textit{cn}'\) (typed with \({\mathbb {k}}'\)), we prove that the dependencies of \({\mathbb {k}}'\) are contained in \({\mathbb {k}}\). Basically, we prove that the following diagram holds:

Hence, the analysis \(\langle {\mathcal{L}},{\mathcal{L}'}\rangle \) contains all the dependencies \(A_i\) that the program can have at runtime, and thus, if the program has a deadlock, the analysis would have a circularity.
In the following, we introduce how we compute the dependencies of a runtime contract. This computation is difficult in general, but in case the runtime contract is as we constructed it in the subject-reduction theorem, then the definition is very simple. First, let say that a contract \({\mathbb {c}}\,\hbox {that}\) does not contain any future is closed. It is clear that we can compute \({\mathbb {c}}(\textsc {act}_{[n]})\) when \({\mathbb {c}}\,\hbox {is}\) closed.
Proposition 5
Let \({\varDelta }\vdash \textit{cn}\mathrel {:}{\mathbb {k}}\) be a typing derivation constructed as in the proof of Theorem 4. Then, \({\mathbb {k}}\) is well formed and  where \({\mathbb {c}}\,\,\hbox {and}\)
\({\mathbb {c}}'\) are closed.
where \({\mathbb {c}}\,\,\hbox {and}\)
\({\mathbb {c}}'\) are closed.
Proof
The first property is already stated in Lemma 1. The second property comes from the fact that when we create a new future \(f\) (in the Asynchronous calls case for instance), we map it in \({\varDelta }'\) to its father process, which will then reference \(f\) because of the \({ rt\_unsync}(\cdot )\) function. Hence, if we consider the relation of which future references which other future in \({\mathbb {k}}\), we get a dependency graph in the shape of a directed tree, where the root is \(f_{ start}\). So,  reduces to a simple pair of contract of the form \(\langle {{\mathbb {c}}},{{\mathbb {c}}'}\rangle ^{\mathrm{start}}_{f_{ start}}\) where \({\mathbb {c}}\,\,\hbox {and}\)
\({\mathbb {c}}'\) are closed.
reduces to a simple pair of contract of the form \(\langle {{\mathbb {c}}},{{\mathbb {c}}'}\rangle ^{\mathrm{start}}_{f_{ start}}\) where \({\mathbb {c}}\,\,\hbox {and}\)
\({\mathbb {c}}'\) are closed.
\(\square \)
In the following, we will suppose that all runtime contracts \({\mathbb {k}}\) come from a type derivation constructed as in Theorem 4.
Definition 13
The semantics of a closed runtime pair (unique upto remaining of cog names) for the saturation at \(i\), noted \([\![{\langle {{\mathbb {c}}},{{\mathbb {c}}'}\rangle ^{c}_{f}}]\!]_{n}\), is defined as  . We extend that definition for any runtime contract with
. We extend that definition for any runtime contract with  .
.
Now we can compute the dependencies of a runtime contract, and we can prove our first property: The analysis performed at static time contains all the dependencies of the initial runtime contract of the program (note that  is the analysis performed at static time, and \([\![{\sigma (\langle {{\mathbb {c}}},{{\mathbb {c}}'}\rangle ^{\mathrm{start}}_{f_{ start}})}]\!]_{n}\) is the set of dependencies of the initial runtime contract of the program):
is the analysis performed at static time, and \([\![{\sigma (\langle {{\mathbb {c}}},{{\mathbb {c}}'}\rangle ^{\mathrm{start}}_{f_{ start}})}]\!]_{n}\) is the set of dependencies of the initial runtime contract of the program):
Proposition 6
Let \(P=\bar{I}\ \bar{C}\ \{\overline{T\ x}; s\}\) be a core ABS program and let \({\varGamma } \vdash P \mathrel {:}\textsc {cct},\,\langle {{\mathbb {c}}},{{\mathbb {c}}'}\rangle \, \rhd \, \mathcal {U}\). Let also \(\sigma \) be a substitution satisfying \(\mathcal {U}\). Then, we have that  .
.
Proof
The result is direct with an induction on \({\mathbb {c}}\,\hbox {and}\)
\({\mathbb {c}}'\), and with the fact that \(+\),  and \(\parallel \) are monotone with respect to \(\Subset \). \(\square \)
and \(\parallel \) are monotone with respect to \(\Subset \). \(\square \)
We now prove the second property: All the dependencies of a program at a given time is included in the dependencies generated from its contract.
Proposition 7
Let suppose \({\varDelta }\vdash _R \textit{cn}\mathrel {:}{\mathbb {k}}\) and let \(A\) be the set of dependencies of \(\textit{cn}\). Then, with \([\![{{\mathbb {k}}}]\!]_{n}=\langle {\mathcal{L}},{\mathcal{L}'}\rangle \), we have \(A\subset \mathcal{L}\).
Proof
By Definition 2, if \(\textit{cn}\) has a dependency \((c,c')\), then there exist \(\textit{cn}_1=\textit{ob}(o,a,\{l | x=e.\mathtt{get};s\},q)\in \textit{cn}\), \(\textit{cn}_2=\textit{fut}(f,\bot )\in \textit{cn}\) and \(\textit{cn}_3=\textit{ob}(o',a',p',q') \in \textit{cn}\) such that \([\![e]\!]_{(a+l)} = l'(\text {destiny}) = f\), \(\{l'\mid s'\}\in p'\cup q'\) and \(a(\textit{cog})=c\) and \(a'(\textit{cog})=c'\). By runtime typing rules (TR-Object), (TR-Process), (TR-Seq) and (TR-Get-Runtime), the contract of \(\textit{cn}_1\) is

we indeed know that the dependency in the contract is toward \(c'\) because of (TR-Invoc) or (TR-Process). Hence,  . It follows, with the lam transformation rule (L-GAinvk), that \((c,c')\) is in \(\mathcal{L}\). \(\square \)
. It follows, with the lam transformation rule (L-GAinvk), that \((c,c')\) is in \(\mathcal{L}\). \(\square \)
Proposition 8
Given two runtime contracts \({\mathbb {k}}\) and \({\mathbb {k}}'\) with \({\mathbb {k}}\trianglerighteq {\mathbb {k}}'\), we have that \([\![{{\mathbb {k}}'}]\!]_{n}\Subset [\![{{\mathbb {k}}}]\!]_{n}\).
Proof
We refer to the rules (LS-*) of the later-stage relation defined in Fig. 27 and to the lam transformation rules (L-*) defined in Fig. 16. The result is clear for the rules (LS-Global), (LS-Fut), (LS-Empty), (LS-Delete) and (LS-Plus). The result for the rule (LS-Bind) is a consequence of (L-AInvk). The result for the rule (LS-AInvk) is a consequence of the definition of \(\Rightarrow \). The result for the rule (LS-SInvk) is a consequence of the definition of \(\Rightarrow \) and (L-SInvk). The result for the rule (LS-RSInvk) is a consequence of the definition of \(\Rightarrow \) and (L-RSInvk). Finally, the result for the rule (LS-DepNull) is a consequence of the definition of \(\Rightarrow \). \(\square \)
We can finally conclude by putting all these results together.
Theorem 5
If a program \(P\) has a deadlock at runtime, then its abstract semantics saturated at n contains a circle.
Proof
This property is a direct consequence of Propositions 6, 7 and 8. \(\square \)
Appendix 3: Properties of Sect. 6
The next theorem states the correctness of our model-checking technique.
Below we write  , if
, if  and \(n\) is the order of
and \(n\) is the order of  .
.
Theorem 6
Let \((\textsc {ct}, \{ \overline{T \ x ~\text{; }~} s \}, \textsc {cct})\) be a core ABS program and \(\textit{cn}\) be a configuration of its operational semantics.
-
1.
If \(\textit{cn}\) has a circularity, then a circularity occurs in \([\![ \textit{cn} ]\!]_{[n]}\);
-
2.
if \(\textit{cn}\rightarrow \textit{cn}'\) and \([\![ \textit{cn}' ]\!]_{[n]}\) has a circularity, then a circularity is already present in \([\![ \textit{cn} ]\!]_{[n]}\);
-
3.
let \(\imath \) be an injective renaming of cog names; \([\![ \textit{cn} ]\!]_{[n]}\) has a circularity if and only if \([\![ \imath (\textit{cn}) ]\!]_{[n]}\) has a circularity.
Proof
To demonstrate item 1, let

We prove that every dependencies occurring in \(\textit{cn}\) is also contained in one state of  . By Definition 2, if \(\textit{cn}\) has a dependency \(({ c},{ c}')\), then it contains \(\textit{cn}'' = \textit{ob}(o,a,\{l | x=e.\mathtt{get};s\},q) \quad \textit{fut}(f,\bot )\), where \(f=[\![e]\!]_{(a+l)}\), \(a(\textit{cog})=c\) and there is \(\textit{ob}(o',a',\{l' | s'\},q')\in \textit{cn}\) such that \(a'(\textit{cog})=c'\) and \(l'(\text {destiny})=f\). By the typing rules, the contract of \(\textit{cn}'\) is
. By Definition 2, if \(\textit{cn}\) has a dependency \(({ c},{ c}')\), then it contains \(\textit{cn}'' = \textit{ob}(o,a,\{l | x=e.\mathtt{get};s\},q) \quad \textit{fut}(f,\bot )\), where \(f=[\![e]\!]_{(a+l)}\), \(a(\textit{cog})=c\) and there is \(\textit{ob}(o',a',\{l' | s'\},q')\in \textit{cn}\) such that \(a'(\textit{cog})=c'\) and \(l'(\text {destiny})=f\). By the typing rules, the contract of \(\textit{cn}'\) is  , where, by typing rule (T-Configurations), \(f\) is actually replaced by a \({\mathtt{C}}!{\mathtt{m}}\,\mathbb {r}(\bar{\mathbb {s}})\rightarrow \mathbb {s}\) produced by a concurrent \(\textit{invoc}\) configuration, or by the contract pair
, where, by typing rule (T-Configurations), \(f\) is actually replaced by a \({\mathtt{C}}!{\mathtt{m}}\,\mathbb {r}(\bar{\mathbb {s}})\rightarrow \mathbb {s}\) produced by a concurrent \(\textit{invoc}\) configuration, or by the contract pair  corresponding to the method body.
corresponding to the method body.
As a consequence  .
.
Let  , with
, with  , then
, then

In general, if \(k\) dependencies occur in a state \(\textit{cn}\), then there is \(\textit{cn}''\subseteq \textit{cn}\) that collects all the tasks manifesting the dependencies.

By definition of \(\parallel \) composition in Sect. 5, the initial state contains all the above pairs \(({ c}_i,{ c}'_i)\).
Let us prove the item 2. We show that the transition \(\textit{cn} {\mathop {\longrightarrow }\limits ^{}} \textit{cn}'\) does not produce new dependencies. That is, the set of dependencies in the states of \([\![ \textit{cn}' ]\!]_{[n]}\) is equal to or smaller than the set of dependencies in the states of \([\![ \textit{cn} ]\!]_{[n]}\).
By Theorem 4, if \({\varDelta }\vdash _R\textit{cn}\!:{\mathbb {k}}\), then \({\varDelta }'\vdash _R\textit{cn}'\!:{\mathbb {k}}'\), with \({\mathbb {k}}\trianglerighteq {\mathbb {k}}'\). We refer to the rules (LS-*) of the later-stage relation defined in Fig. 27 and to the contract reduction rules (Red-*) defined in Fig. 19. The result is clear for the rules (LS-Global), (LS-Fut), (LS-Empty), (LS-Delete) and (LS-Plus). The result for the rule (LS-Bind) is a consequence of (Red-AInvk). The result for the rule (LS-AInvk) is a consequence of the definition of \(\Rightarrow \). The result for the rule (LS-SInvk) is a consequence of the definition of \(\Rightarrow \) and (Red-SInvk). The result for the rule (LS-RSInvk) is a consequence of the definition of \(\Rightarrow \) and (Red-RSInvk). Finally, the result for the rule (LS-DepNull) is a consequence of the definition of \(\Rightarrow \).
Item 3 is obvious because circularities are preserved by injective renamings of cog names. \(\square \)
Rights and permissions
About this article
Cite this article
Giachino, E., Laneve, C. & Lienhardt, M. A framework for deadlock detection in core ABS . Softw Syst Model 15, 1013–1048 (2016). https://doi.org/10.1007/s10270-014-0444-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10270-014-0444-y











 and all futures
and all futures  and
and  .
.

 . It is easy to see that
. It is easy to see that  which proves that
which proves that 


 and
and  such that
such that  . By construction of the type system (in particular, the rules
. By construction of the type system (in particular, the rules  and such that
and such that  (with
(with  and
and  is checked). By construction of the rt_unsync function, there exist a term
is checked). By construction of the rt_unsync function, there exist a term  and
and 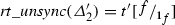 . Finally, if we note
. Finally, if we note  (as
(as 


 and
and  and
and  . By rules
. By rules 
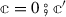 (
(
