On the maximum feasible subsystem problem, IISs and IIS-hypergraphs

Abstract.

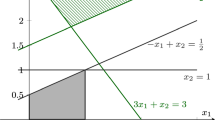
 We consider the Max FS problem: For a given infeasible linear system A x≤b, determine a feasible subsystem containing as many inequalities as possible. This problem, which is NP-hard and also difficult to approximate, has a number of interesting applications in a wide range of fields. In this paper we examine structural and algorithmic properties of Max FS and of Irreducible Infeasible Subsystems (IISs), which are intrinsically related since one must delete at least one constraint from each IIS to attain feasibility. First we provide a new simplex decomposition characterization of IISs and prove that finding a smallest cardinality IIS is very difficult to approximate. Then we discuss structural properties of IIS-hypergraphs, i.e., hypergraphs in which each edge corresponds to an IIS, and show that recognizing IIS-hypergraphs subsumes the Steinitz problem for polytopes and hence is NP-hard. Finally we investigate rank facets of the Feasible Subsystem polytope whose vertices are incidence vectors of feasible subsystems of a given infeasible system. In particular, using the IIS-hypergraph structural result, we show that only two very specific types of rank inequalities induced by generalized antiwebs (which generalize cliques, odd holes and antiholes to general independence systems) can arise as facets.