iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://unpaywall.org/10.1007/S00521-019-04115-X
Stability property of impulsive inertial neural networks with unbounded time delay and saturating actuators | Neural Computing and Applications Skip to main content
Springer Nature Link
Log in

Stability property of impulsive inertial neural networks with unbounded time delay and saturating actuators

  • Multi-Source Data Understanding (MSDU)
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

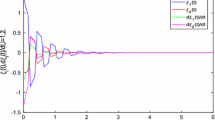
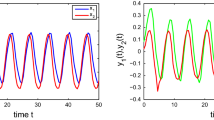
This paper considers the stability property of impulsive inertial neural networks with unbounded delay and saturating actuators. Based on polytopic representation approach, some sufficient conditions to ensure global asymptotic stability are obtained for impulsive inertial neural networks. By using Lyapunov function with the matrix form of 2-norm, we obtain some conditions to ensure the stability of impulsive inertial neural networks. Finally, the validity of this method is verified by several simulation examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Bemporad A (1998) Predictive control of teleoperated constrained systems with unbounded communication delays. IEEE Conf Decis Control 2:2133–2138

    Google Scholar 

  2. Chaouki A (2016) Neutral impulsive shunting inhibitory cellular neural networks with time-varying coefficients and leakage delays. Cognit Neurodyn 10(6):573–591

    Google Scholar 

  3. Ding L, Zheng WX, Guo G (2018) Network-based practical set consensus of multi-agent systems subject to input saturation. Automatica 89:316–324

    MathSciNet  MATH  Google Scholar 

  4. Esteves S, Oliveira JJ (2015) Global asymptotic stability of nonautonomous Cohen–Grossberg neural network models with infinite delays. Appl Math Comput 265:333–346

    MathSciNet  MATH  Google Scholar 

  5. Guan Z, Chen G (1999) On delayed impulsive Hopfield neural networks. Neural Netw 12(2):273–280

    Google Scholar 

  6. Hu T, Lin Z (2001) Control systems with actuator saturation: analysis and design. Springer, New York

    MATH  Google Scholar 

  7. Huang H, Li D, Lin Z, Xi Y (2011) An improved robust model predictive control design in the presence of actuator saturation. Automatica 47(4):861–864

    MathSciNet  MATH  Google Scholar 

  8. Li C, Gao DY, Liu C, Chen G (2014) Impulsive control for synchronizing delayed discrete complex networks with switching topology. Neural Comput Appl 24(1):59–68

    Google Scholar 

  9. Li H, Jiang H, Hu C (2016) Existence and global exponential stability of periodic solution of memristor-based BAM neural networks with time-varying delays. Neural Netw 75:97–109

    MATH  Google Scholar 

  10. Li H, Li C, Huang T (2017) Periodicity and stability for variable-time impulsive neural networks. Neural Netw 94:24–33

    MATH  Google Scholar 

  11. Li H, Li C, Huang T, Zhang W (2018) Fixed-time stabilization of impulsive cohen-grossberg BAM neural networks. Neural Netw 98:203–211

    MATH  Google Scholar 

  12. Li H, Zhang W, Li C, Zhang W (2018) Global asymptotical stability for a class of non-autonomous impulsive inertial neural networks with unbounded time-varying delay. Neural Comput Appl. https://doi.org/10.1007/s00521-018-3498-x

    Google Scholar 

  13. Li L, Li C, Li H (2018) Fully state constraint impulsive control for non-autonomous delayed nonlinear dynamic systems. Nonlinear Anal Hybrid Syst 29:383–394

    MathSciNet  MATH  Google Scholar 

  14. Li X, Cao J (2017) An impulsive delay inequality involving unbounded time-varying delay and applications. IEEE Trans Autom Control 62(7):3618–3625

    MathSciNet  MATH  Google Scholar 

  15. Li X, Rakkiyappan R (2013) Impulsive controller design for exponential synchronization of chaotic neural networks with mixed delays. Commun Nonlinear Sci Numer Simul 18(6):1515–1523

    MathSciNet  MATH  Google Scholar 

  16. Li X, Zhang X, Song S (2017) Effect of delayed impulses on input-to-state stability of nonlinear systems. Automatica 76:378–382

    MathSciNet  MATH  Google Scholar 

  17. Li Z, Fang J, Huang T, Miao Q, Wang H (2018) Impulsive synchronization of discrete-time networked oscillators with partial input saturation. Inf. Sci. 422:531–541

    Google Scholar 

  18. Lin X, Li X, Zou Y, Li S (2014) Finite-time stabilization of switched linear systems with nonlinear saturating actuators. J Frankl Inst 351(3):1464–1482

    MathSciNet  MATH  Google Scholar 

  19. Liu B (2016) Global exponential convergence of non-autonomous cellular neural networks with multi-proportional delays. Neurocomputing 191:352–355

    Google Scholar 

  20. Mauro A, Contiand F, Dodge F, Schor R (1970) Subthreshold behavior and phenomenological impedance of the squid giant axon. J Gen Physiol 55(4):497–523

    Google Scholar 

  21. Song X, Zhao P, Xing Z, Peng J (2016) Global asymptotic stability of CNNS with impulses and multi-proportional delays. Math Methods Appl Sci 39(4):722–733

    MathSciNet  MATH  Google Scholar 

  22. Tu Z, Cao J, Alsaedi A, Alsaadi FE (2017) Global dissipativity of memristor-based neutral type inertial neural networks. Neural Netw 88:125–133

    MATH  Google Scholar 

  23. Tu Z, Cao J, Hayat T (2016) Matrix measure based dissipativity analysis for inertial delayed uncertain neural networks. Neural Netw 75:47–55

    MATH  Google Scholar 

  24. Wan P, Jian J (2017) Global convergence analysis of impulsive inertial neural networks with time-varying delays. Neurocomputing 245:68–76

    Google Scholar 

  25. Wheeler DW, Schieve WC (1997) Stability and chaos in an inertial two-neuron system. Phys D Nonlinear Phenom 105(4):267–284

    MATH  Google Scholar 

  26. Xu S, Lam J (2006) A new approach to exponential stability analysis of neural networks with time-varying delays. Neural Netw 19(1):76–83

    MATH  Google Scholar 

  27. Yang X, Cao J, Yang Z (2013) Synchronization of coupled reaction-diffusion neural networks with time-varying delays via pinning-impulsive controller. SIAM J Control Optim 51(5):3486–3510

    MathSciNet  MATH  Google Scholar 

  28. Zeng Z, Wang J (2005) Liao X (2005) Global asymptotic stability and global exponential stability of neural networks with unbounded time-varying delays. IEEE Trans Circuits Syst 52–II(3):168–173

    MathSciNet  Google Scholar 

  29. Zhang A (2018) Almost periodic solutions for SICNNs with neutral type proportional delays and D operators. Neural Process Lett 47(1):57–70

    Google Scholar 

  30. Zhao ZJ, Song QK, Zhang JY (2006) Exponential periodicity and stability of neural networks with reaction-diffusion terms and both variable and unbounded delays. Comput Math Appl 51(3–4):475–486

    MathSciNet  MATH  Google Scholar 

  31. Zhou B, Gao H, Lin Z, Duan G (2012) Stabilization of linear systems with distributed input delay and input saturation. Automatica 48(5):712–724

    MathSciNet  MATH  Google Scholar 

  32. Zhu S, Luo W, Li J, Shen Y (2014) Robustness of globally exponential stability of delayed neural networks in the presence of random disturbances. Neural Comput Appl 25(3–4):743–749

    Google Scholar 

Download references

Acknowledgements

This work was supported by the National Nature Science Foundation of China (Grant Nos. 61672133, 61832001 and 61632007).

Author information

Authors and Affiliations

  1. Center for Future Media, School of Computer Science and Engineering, University of Electronic Science and Technology of China, Chengdu, 611731, China

    Deqiang Ouyang & Jie Shao

  2. College of Mathematics and System Sciences, Xinjiang University, Urumqi, 830046, China

    Cheng Hu

Authors
  1. Deqiang Ouyang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jie Shao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Cheng Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jie Shao.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ouyang, D., Shao, J. & Hu, C. Stability property of impulsive inertial neural networks with unbounded time delay and saturating actuators. Neural Comput & Applic 32, 6571–6580 (2020). https://doi.org/10.1007/s00521-019-04115-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-019-04115-x

Keywords

Search

Navigation