iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://unpaywall.org/10.1007/S00500-021-05666-9
An improved expression for information quality of basic probability assignment and its application in target recognition | Soft Computing Skip to main content
Springer Nature Link
Log in

An improved expression for information quality of basic probability assignment and its application in target recognition

  • Methodologies and Application
  • Published:
Soft Computing Aims and scope Submit manuscript

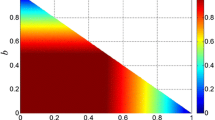
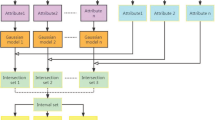
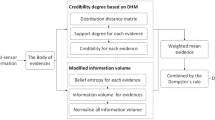
Abstract

Information quality is widely used in many applications. However, how to measure information quality in basic probability assignment accurately is still an open issue. Generalized expression for information quality is an effective method to measure information quality in basic probability assignment. Nevertheless, the counter-intuitive results may be obtained when statements are of intersection. To address this issue, a new expression for information quality of basic probability assignment is proposed in this paper considering the frame of discernment and the influence of intersection among statements which can cause changes of uncertainty. Numerical examples are illustrated to demonstrate the effectiveness of the proposed method. In addition, an application in target recognition is used to show the validity of proposed form of information quality in combining conflicting evidences.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Babajanyan S, Allahverdyan A, Cheong KH (2020) Energy and entropy: path from game theory to statistical mechanics. Phys Rev Res 2(4):043055

    Article  Google Scholar 

  • Benettin G, Galgani L, Strelcyn JM (1976) Kolmogorov entropy and numerical experiments. Phys Rev A 14(6):2338

    Article  Google Scholar 

  • Cao Z, Ding W, Wang YK, Hussain FK, Al-Jumaily A, Lin CT (2020) Effects of repetitive SSVEPs on EEG complexity using multiscale inherent fuzzy entropy. Neurocomputing 389:198–206

    Article  Google Scholar 

  • Dempster AP (1967) Upper and lower probabilities induced by a multi-valued mapping. Ann Math Stat 38(2):325–339

    Article  Google Scholar 

  • Deng Y (2020) Uncertainty measure in evidence theory. Sci China Inf Sci 63(11):1–19

    Article  MathSciNet  Google Scholar 

  • Deng Y (2020) Information volume of mass function. Int J Comput Commun Control 15(6):3983

    Article  Google Scholar 

  • Deng J, Deng Y (2021) Information volume of fuzzy membership function. Int J Comput Commun Control 16(1):4106

    Article  Google Scholar 

  • Dvurečenskij A, Lachman D (2020) Spectral resolutions and observables in n-perfect MV-algebras. Soft Comput 24(2):843–860

    Article  Google Scholar 

  • Dvurečenskij A, Zahiri O (2019) States on EMV-algebras. Soft Comput 23(17):7513–7536

    Article  Google Scholar 

  • Fan L, Deng Y (2020) Determine the number of unknown targets in Open World based on Elbow method. IEEE Trans Fuzzy Syst. https://doi.org/10.1109/TFUZZ.2020.2966182

    Article  Google Scholar 

  • Fei L, Lu J, Feng Y (2020) An extended best-worst multi-criteria decision-making method by belief functions and its applications in hospital service evaluation. Comput Ind Eng 142:106355

    Article  Google Scholar 

  • Garrido P, Goldstein S, Lebowitz JL (2004) Boltzmann entropy for dense fluids not in local equilibrium. Phys Rev Lett 92(5):050602

    Article  Google Scholar 

  • Gini C, Pizetti E, Salvemini T (1912) Reprinted in Memorie di metodologica statistica. Rome: Libreria Eredi Virgilio Veschi 1

  • Jiang W, Cao Y, Deng X (2019) A novel Z-network model based on Bayesian network and Z-number. IEEE Trans Fuzzy Syst 28:1585–1599

    Article  Google Scholar 

  • Jousselme AL, Grenier D, Bossé Éloi (2001) A new distance between two bodies of evidence. Inf Fusion 2(2):91–101

    Article  Google Scholar 

  • Lai JW, Chang J, Ang LK, Cheong KH (2020) Multi-level information fusion to alleviate network congestion. Inf Fusion 63:248–255. https://doi.org/10.1016/j.inffus.2020.06.006

    Article  Google Scholar 

  • Lefevre E, Colot O, Vannoorenberghe P (2002) Belief function combination and conflict management. Inf Fusion 3(2):149–162

    Article  Google Scholar 

  • Li D, Deng Y (2019) A new correlation coefficient based on generalized information quality. IEEE Access 7:175411–175419

    Article  Google Scholar 

  • Li Y, Xiao F (2019) Aggregation of uncertainty data based on ordered weighting aggregation and generalized information quality. Int J Intell Syst 34:1653–1666

    Article  Google Scholar 

  • Li D, Gao X, Deng Y (2019) A generalized expression for information quality of basic probability assignment. IEEE Access 7:174734–174739

    Article  Google Scholar 

  • Li M, Huang S, De Bock J, De Cooman G, Pižurica A (2020) A robust dynamic classifier selection approach for hyperspectral images with imprecise label information. Sensors 20(18):5262

    Article  Google Scholar 

  • Li Y, Pelusi D, Deng Y (2020) Generate two-dimensional belief function based on an improved similarity measure of trapezoidal fuzzy numbers. Comput Appl Math 39(4):1–20

    MathSciNet  Google Scholar 

  • Li D, Deng Y, Cheong KH (2021) Multi-source basic probability assignment fusion based on information quality. Int J Intell Syst. https://doi.org/10.1002/int.22363

    Article  Google Scholar 

  • Liang S, Deng X, Jiang W (2019) Optimal data fusion based on information quality function. Appl Intell 49:3938–3946

    Article  Google Scholar 

  • Liao H, Ren Z, Fang R (2020) A Deng-entropy-based evidential reasoning approach for multi-expert multi-criterion decision-making with uncertainty. Int J Comput Intell Syst 13:1281–1294. https://doi.org/10.2991/ijcis.d.200814.001

    Article  Google Scholar 

  • Liu W (2006) Analyzing the degree of conflict among belief functions. Artif Intell 170(11):909–924

    Article  MathSciNet  Google Scholar 

  • Liu Z, Zhang Z, Liu Y, Dezert J, Pan Q (2019) A new pattern classification improvement method with local quality matrix based on K-NN. Knowl Based Syst 164:336–347. https://doi.org/10.1016/j.knosys.2018.11.001

    Article  Google Scholar 

  • Liu F, Gao X, Zhao J, Deng Y (2019) Generalized belief entropy and its application in identifying conflict evidence. IEEE Access 7:126625–126633

    Article  Google Scholar 

  • Liu T, Li C, Wang C, Lai J, Cheong K (2020) A simple-FSDT-based isogeometric method for piezoelectric functionally graded plates. Mathematics 8:2177. https://doi.org/10.3390/math8122177

    Article  Google Scholar 

  • Liu Z, Liu Y, Dezert J, Cuzzolin F (2020) Evidence combination based on credal belief redistribution for pattern classification. IEEE Trans Fuzzy Syst 28(4):618–631. https://doi.org/10.1109/TFUZZ.2019.2911915

    Article  Google Scholar 

  • Liu Q, Cui H, Tian Y, Kang B (2020) On the Negation of discrete Z-numbers. Inf Sci 537:18–29

    Article  MathSciNet  Google Scholar 

  • Luo Z, Deng Y (2020) A vector and geometry interpretation of basic probability assignment in Dempster–Shafer theory. Int J Intell Syst 35(6):944–962

    Article  Google Scholar 

  • Murphy CK (2000) Combining belief functions when evidence conflicts. Decis Support Syst 29(1):1–9

    Article  Google Scholar 

  • Pan Y, Zhang L, Wu X, Skibniewski MJ (2020) Multi-classifier information fusion in risk analysis. Inf Fusion 60:121–136

    Article  Google Scholar 

  • Rényi A, et al. (1961) On measures of entropy and information. In: Proceedings of the fourth berkeley symposium on mathematical statistics and probability, Volume 1: contributions to the theory of statistics, The Regents of the University of California

  • Ruan J, Wang Z, Chan F, Patnaik S, Tiwari M (2020) A reinforcement learning-based algorithm for the aircraft maintenance routing problem. Expert Syst Appl 169:114399. https://doi.org/10.1016/j.eswa.2020.114399

    Article  Google Scholar 

  • Shafer G (1976) A mathematical theory of evidence, vol 42. Princeton university press

  • Shannon CE (1948) A mathematical theory of communication. Bell Syst Tech J 27(3):379–423

    Article  MathSciNet  Google Scholar 

  • Song X, Qin B, Xiao F (2020) FR–KDE: a hybrid fuzzy rule-based information fusion method with its application in biomedical classification. Int J Fuzzy Syst pp 1–13. https://doi.org/10.1007/s40815-020-00957-z

  • Tang SW, Zhou ZJ, Hu CH, Yang JB, Cao Y (2019) Perturbation analysis of evidential reasoning rule. IEEE Trans Syst Man Cybern Syst. https://doi.org/10.1109/TSMC.2019.2944640

  • Tao R, Liu Z, Cai R, Cheong KH (2021) A dynamic group MCDM model with intuitionistic fuzzy set: perspective of alternative queuing method. Inf Sci 555:85–103

    Article  MathSciNet  Google Scholar 

  • Tian Y, Liu L, Mi X, Kang B (2020) ZSLF: a new soft likelihood function based on Z-numbers and its application in expert decision system. IEEE Trans Fuzzy Syst. https://doi.org/10.1109/TFUZZ.2020.2997328

  • Tsallis C (1988) Possible generalization of Boltzmann-Gibbs statistics. J Stat Phys 52(1–2):479–487

    Article  MathSciNet  Google Scholar 

  • Tsallis C (2009) Nonadditive entropy: the concept and its use. Eur Phys J A 40(3):257

    Article  MathSciNet  Google Scholar 

  • Wang C, Zhi-Xuan T, Ye Y, Wang L, Cheong K, Xie Ng (2017) A rumor spreading model based on information entropy. Sci Rep. https://doi.org/10.1038/s41598-017-09171-8

    Article  Google Scholar 

  • Wang T, Wei X, Huang T, Wang J, Valencia-Cabrera L, Fan Z, Pérez-Jiménez MJ (2019) Cascading failures analysis considering extreme virus propagation of cyber-physical systems in smart grids. Complexity. https://doi.org/10.1155/2019/7428458

    Article  Google Scholar 

  • Wang T, Wei X, Wang J, Huang T, Peng H, Song X, Cabrera LV, Perez-Jimenez MJ (2020a) A weighted corrective fuzzy reasoning spiking neural P system for fault diagnosis in power systems with variable topologies. Eng Appl Artif Intell 92:103680

    Article  Google Scholar 

  • Wang T, Liu W, Zhao J, Guo X, Terzija V (2020b) A rough set-based bio-inspired fault diagnosis method for electrical substations. Int J Electr Power Energy Syst 119:105961. https://doi.org/10.1016/j.ijepes.2020.105961

    Article  Google Scholar 

  • Wang H, Fang YP, Zio E (2021) Risk assessment of an electrical power system considering the influence of traffic congestion on a hypothetical scenario of electrified transportation system in New York state. IEEE Trans Intell Transp Syst 22(1):142–155. https://doi.org/10.1109/TITS.2019.2955359

    Article  Google Scholar 

  • Xiao F (2019) A distance measure for intuitionistic fuzzy sets and its application to pattern classification problems. IEEE Trans Syst Man Cybern Syst. https://doi.org/10.1109/TSMC.2019.2958635

  • Xiao F (2019) EFMCDM: evidential fuzzy multicriteria decision making based on belief entropy. IEEE Trans Fuzzy Syst 28:1477–1491

    Google Scholar 

  • Xiao F (2020) A new divergence measure for belief functions in D-S evidence theory for multisensor data fusion. Inf Sci 514:462–483

    Article  MathSciNet  Google Scholar 

  • Xue Y, Deng Y (2020) On the conjunction of possibility measures under intuitionistic evidence sets. J Ambient Intell Hum Comput. https://doi.org/10.1007/s12652-020-02508-8

    Article  Google Scholar 

  • Yager RR (1987) On the Dempster–Shafer framework and new combination rules. Inf Sci 41(2):93–137

    Article  MathSciNet  Google Scholar 

  • Yager RR, Petry F (2016) An intelligent quality-based approach to fusing multi-source probabilistic information. Inf Fusion 31:127–136

    Article  Google Scholar 

  • Ye Y, Cheong K, Cen Y, Ng X (2016) Effects of behavioral patterns and network topology structures on parrondo’s paradox. Sci Rep 6:37028. https://doi.org/10.1038/srep37028

    Article  Google Scholar 

  • Ye Y, Hang XR, Koh JM, Miszczak JA, Cheong KH, Gang Xie N (2020) Passive network evolution promotes group welfare in complex networks. Chaos Solitons Fractals 130:109464. https://doi.org/10.1016/j.chaos.2019.109464

    Article  MathSciNet  Google Scholar 

  • Yong D, WenKang S, ZhenFu Z, Qi L (2004) Combining belief functions based on distance of evidence. Decis Support Syst 38(3):489–493

    Article  Google Scholar 

  • Zadeh LA (1986) A simple view of the Dempster–Shafer theory of evidence and its implication for the rule of combination. Ai Mag 7(2):85–90

    Google Scholar 

  • Zhang Z, Liu T, Chen D, Zhang W (2014) Novel algorithm for identifying and fusing conflicting data in wireless sensor networks. Sensors 14(6):9562–9581

    Article  Google Scholar 

Download references

Acknowledgements

The authors greatly appreciate meticulous suggestions of anonymous reviewers and the encouragement of editor. This research is supported by the Fundamental Research Funds for the Central Universities (No. SWU1909785) and Training Program of Innovation and Entrepreneurship for Undergraduates of Chongqing City (No. S202010635174).

Author information

Authors and Affiliations

  1. School of Computer and Information Science, Southwest University, No. 2 Tiansheng Road, BeiBei District, Chongqing, 400715, China

    Hanwen Li

  2. Business College, Southwest University, No.160 Xueyuan Road, Rongchang District, Chongqing, 402460, China

    Rui Cai

Authors
  1. Hanwen Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rui Cai
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rui Cai.

Ethics declarations

Conflict of interest

All the authors certify that there is no conflict of interest with any individual or organization for the present work. This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, H., Cai, R. An improved expression for information quality of basic probability assignment and its application in target recognition. Soft Comput 25, 6681–6690 (2021). https://doi.org/10.1007/s00500-021-05666-9

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-021-05666-9

Keywords

Search

Navigation