Abstract
Density peaks clustering (DPC) algorithm is a novel algorithm that efficiently deals with the complex structure of the data sets by finding the density peaks. It needs neither iterative process nor more parameters. The density–distance is utilized to find the density peaks in the DPC algorithm. But unfortunately, it will divide one cluster into multiple clusters if there are multiple density peaks in one cluster and ineffective when data sets have relatively higher dimensions. To overcome the first problem, we propose a FDPC algorithm based on a novel merging strategy motivated by support vector machine. First, the strategy utilizes the support vectors to calculate the feedback values between every two clusters after clustering based on the DPC. Then, it merges clusters to obtain accurate clustering results in a recursive way according to the feedback values. To address the second limitation, we introduce nonnegative matrix factorization into the FDPC to preprocess high-dimensional data sets before clustering. The experimental results on real-world data sets and artificial data sets demonstrate that our algorithm is robust and flexible and can recognize arbitrary shapes of the clusters effectively regardless of the space dimension and outperforms DPC.












Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Bai L, Cheng X, Liang J et al (2017) Fast density clustering strategies based on the k-means algorithm. Pattern Recogn 71:375–386
Birant D, Kut A (2007) ST-DBSCAN: an algorithm for clustering spatial-temporal data. Data Know Eng 60(1):208–221
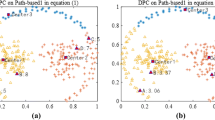
Chang H, Yeung DY (2008) Robust path-based spectral clustering. Pattern Recogn 41(1):191–203
Deng L (2012) The MNIST database of handwritten digit images for machine learning research. IEEE Signal Process Mag 29(6):141–142
Ding S, Jia H, Shi Z (2014) Spectral clustering algorithm based on adaptive Nystrom sampling for big data analysis. J Softw 25(9):2037–2049
Ding S, Zhang X, Yu J (2016) Twin support vector machines based on fruit fly optimization algorithm. J Int J Mach Learn Cybern 7(2):193–203
Ding S, Du M, Sun T et al (2017) An entropy-based density peaks clustering algorithm for mixed type data employing fuzzy neighborhood. Know Based Syst 133:294–313
Du M, Ding S, Jia H (2016) Study on density peaks clustering based on k-nearest neighbors and principal component analysis. Knowl Based Syst 99:135–145
Fraley C, Raftery A (2011) Model-based clustering, discriminant analysis, and density estimation. J Am Stat Assoc 97(458):611–631
Frey BJ, Dueck D (2007) Clustering by passing messages between data points. Science 315(5814):972
Gionis A, Mannila H, Tsaparas P (2007) Clustering aggregation. Acm Trans Know Discov Data 1(1):341–352
Gu B, Sheng V (2016) A Robust regularization path algorithm for \(\nu \)-support vector classification. IEEE Trans Neural Netw Learn Syst 1:1–8
Gu B, Sheng V, Wang Z et al (2015) Incremental learning for \(\nu \)-support vector regression. Neural Netw Off J Int Neural Netw Soc 67:140–150
Jia H, Ding S, Du M (2015) Self-tuning p-spectral clustering based on shared nearest neighbors. Cognit Comput 7(5):1–11
Kanungo T, Mount D, Netanyahu NS et al (2002) An efficient k-means clustering algorithm: analysis and implementation. IEEE Trans Pattern Anal Mach Intell 24(7):881–892
Lee DD, Seung HS (2000) Algorithms for non-negative matrix factorization. In: International conference on neural information processing systems. MIT Press, pp 535–541
Lee D, Seung H (1999) Learning the parts of objects by non-negative matrix factorization. Nature 401(6755):788–791
Lee N, Tang R, Priebe C et al (2016) A model selection approach for clustering a multinomial sequence with non-negative factorization. IEEE Trans Pattern Anal Mach Intell 38(12):2345–2358
Li C, Li L, Zhang J et al (2012) Highly efficient and exact method for parallelization of grid-based algorithms and its implementation in DelPhi. J Comput Chem 33(24):1960–1966
Ma Y, Cheng G, Liu Z et al (2017) Fuzzy nodes recognition based on spectral clustering in complex networks. Phys A 465:792–797
Mehmood R, Zhang G, Bie R et al (2016) Clustering by fast search and find of density peaks via heat diffusion. Neurocomputing 208(6191):210–217
Morris K, Mcnicholas P (2016) Clustering, classification, discriminant analysis, and dimension reduction via generalized hyperbolic mixtures. Comput Stat Data Anal 97:133–150
Papadimitriou CH, Steiglitz K (1982) Combinatorial optimization: algorithms and complexity. IEEE Trans Acoust Speech Signal Process 32(6):1258–1259
Rodríguez A, Laio A (2014) Clustering by fast search and find of density peaks. Science 344(6191):1492–1496
Ros F, Guillaume S (2016) DENDIS: a new density-based sampling for clustering algorithm. Expert Syst Appl 56:349–359
Samaria F, Harter A (1994) Parameterisation of a stochastic model for human face identification. Proc Second IEEE Workshop Appl Comput Vis 1995:138–142
Sampat M, Wang Z, Gupta S et al (2009) Complex wavelet structural similarity: a new image similarity index. IEEE Trans Image Process 18(11):2385–2401
Trigeorgis G, Bousmalis K, Zafeiriou S et al (2017) A deep matrix factorization method for learning attribute representations. IEEE Trans Pattern Anal Mach Intell 39(3):417–429
Wang XF, Xu Y (2015) Fast clustering using adaptive density peak detection. Stat Methods Med Res 26(6):2800–281
Xie J, Gao H, Xie W et al (2016) Robust clustering by detecting density peaks and assigning points based on fuzzy weighted K -nearest neighbors. Inf Sci 354:19–40
Zhang Y, Cheny S, Yu G (2016) Efficient Distributed Density Peaks for Clustering Large Data Sets in MapReduce. IEEE Trans Knowl Data Eng 28(12):3218–3230
Zhou L, Pei C (2016) Delta-distance based clustering with a divide-and-conquer strategy: 3DC clustering. Pattern Recogn Lett 73:52–59
Acknowledgements
This work is supported by the Fundamental Research Funds for the Central Universities (No. 2017XKQY076)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest:
All the authors declare that they have no conflict of interest.
Human and animal rights:
This article does not contain any studies with human or animal subjects performed by the any of the authors.
Informed consent:
All procedures followed were in accordance with the ethical standards of the responsible committee on human experimentation (institutional and national) and with the Helsinki Declaration of 1975, as revised in 2008 (5). Additional informed consent was obtained from all patients for which identifying information is included in this article.
Additional information
Communicated by V. Loia.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Xu, X., Ding, S., Xu, H. et al. A feasible density peaks clustering algorithm with a merging strategy. Soft Comput 23, 5171–5183 (2019). https://doi.org/10.1007/s00500-018-3183-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-018-3183-0