Hamilton Circuits and Essential Girth of Claw Free Graphs

Abstract

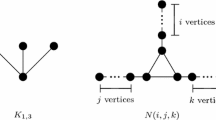
Let $G$ be a $K_{1,3}$-free graph. A circuit of $G$ is essential if it contains a non-locally connected vertex $v$ and passes through both components of $N(v)$. The essential girth of $G$, denoted by $g_e(G)$, is the length of a shortest essential circuit. It can be seen easily that, by Ryjáček closure operation, the essential girth of $G$ is closely related to the girth of $H$ where $H$ is the Ryjáček closure of $G$ and is a line graph. A generalized net, denoted by $N_{i_1,i_2,i_3}$, is a graph obtained from a triangle $C_3$ and three disjoint paths $P_{i_\mu +1}$ ($\mu =1,2,3$), by identifying each vertex $v_\mu$ of $C_3=v_1v_2v_3v_1$ with an end vertex of the path $P_{i_\mu +1}$, for every $\mu = 1,2,3$. In this paper, we prove that every $2$-connected $\{ K_{1,3}, N_{1,1,g_e(G)-4}\}$-free (and $\{ K_{1,3}, N_{1,0,g_e(G)-3}\}$-free) graph $G$ contains a Hamilton circuit. With the additional parameter $g_e$, these results extend some earlier theorems about Hamilton circuits in $\{ K_{1,3}, N_{a,b,c}\}$-free graphs (for some small integers $a, b$ and $c$).