On the modelling of the vibration behaviors via discrete singular convolution method for a high-order sector annular system

Abstract

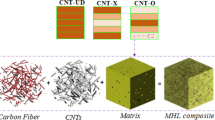
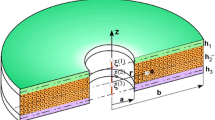
This research presents a numerical investigation on the dynamic information of the axisymmetric sandwich annular sector plate via a higher-order continuum elasticity theory. The sandwich annular sector plate comprises multi-hybrid nanocomposite reinforced (MHCR) face sheets in the top, bottom layers, and a honeycomb core. For modeling the thermal situation and the thickness of the structure, three-kinds of thermal loading are presented. For simulating MHCR face sheets, the role of the mixture and Halpin–Tsai micromechanics model is utilized. For obtaining the governing equations and various boundary conditions, first-order shear deformation theory (FSDT), as well as Hamilton’s principle, are presented. For solving the equations and obtaining eigenvalue, and eigenvector of the current structure, discrete singular convolution method (DSCM) as a numerical one is investigated. Consequently, a parametric study is carried out to examine the impacts of honeycomb network angle, thickness to length ratio of the honeycomb, honeycomb to face sheet thickness ratio, fibers angel, outer to inner radius ratio, and weight fraction of CNTs on the dynamics of the current sandwich structure. The results show that for clamped edge and each t_h/l_h, increasing $\theta_{h} /\pi$ is a reason for decreasing the natural frequency of the disk. Another consequence is that the impact of temperature changes on the frequency of the disk is hardly dependent on the fiber angle. It means that the effect of temperature changes on the frequencies of the current system is more considerable at 0.2 ≤ θ_f ⁄π ≤ 0.4 and 0.6 ≤ θ_f ⁄π ≤ 0.8.

Appendix

The variation of Eqs. (18a–18c) can be achieved as below:

$$ \begin{aligned} \delta O^{*\chi } & = \int\limits_{V} {\rho^{\chi } \left( {\partial_{t} D_{1} \partial_{t} \delta D_{1} + \partial_{t} D_{2} \partial_{t} \delta D_{2} + \partial_{t} D_{3} \partial_{t} \delta D_{3} } \right)}^{\chi } \,{\text{d}}V \\ \delta O^{*\chi } & = \int\limits_{{R_{1} }}^{{R_{2} }} {\int\limits_{0}^{\theta } {\left[ \begin{gathered} \left\{ { - I^{0} \partial_{t}^{2} u_{0} - I^{1} \partial_{t}^{2} u_{1} } \right\}\delta u_{0} + \left\{ { - I^{1} \partial_{t}^{2} u_{0} - I^{2} \partial_{t}^{2} u_{1} } \right\}\delta u_{1} \hfill \\ \left\{ { - I^{0} \partial_{t}^{2} v_{0} - I^{1} \partial_{t}^{2} v_{1} } \right\}\delta v_{0} + \left\{ { - I^{1} \partial_{t}^{2} v_{0} - I^{2} \partial_{t}^{2} v_{1} } \right\}\delta v_{1} + \left\{ { - I^{0} \partial_{t}^{2} w_{0} } \right\}\delta w_{0} \hfill \\ \end{gathered} \right]^{\chi } r{\text{d}}r{\text{d}}\theta } } , \\ \end{aligned} $$

(39)

$$ \begin{aligned} \delta \Theta^{*\chi } & = \frac{1}{2}\iiint\limits_{V} {\sigma_{ij}^{\chi } \delta \varepsilon_{ij}^{\chi } {\text{d}}V} \\ & = \int\limits_{A} {\left[ \begin{gathered} \left( {N^{rr} \partial_{r} \delta u_{\,0\,} + M^{rr} \partial_{r} \delta u_{\,1\,} } \right) \hfill \\ + \left( {\frac{{N^{\theta \theta } }}{r}\partial_{\theta } \delta v_{\,0\,} + \frac{{M^{\theta \theta } }}{r}\partial_{\theta } \delta v_{\,1\,} + \frac{{N^{\theta \theta } }}{r}\delta u_{0\,} + \frac{{M^{\theta \theta } }}{r}\delta u_{1\,} } \right) \hfill \\ + \left( \begin{gathered} N^{r\theta } \partial_{r} \delta v_{\,0\,} + M^{r\theta } \partial_{r} \delta v_{\,1\,} + \frac{{N^{r\theta } }}{r}\partial_{\theta } \delta u_{\,0\,} + \frac{{M^{r\theta } }}{r}\partial_{\theta } \delta u_{\,1\,} \hfill \\ - \frac{{N^{r\theta } }}{r}\delta v_{0} - \frac{{M^{r\theta } }}{r}\delta v_{1} \hfill \\ \end{gathered} \right) \hfill \\ + \left( {(N^{rz} )\left( {\delta u_{1\,} + \partial_{r} \delta w_{\,0\,} } \right)} \right) + \left( {(N^{\theta z} )\left( {\delta v_{1\,} + \frac{1}{r}\partial_{\theta } \delta w_{\,0\,} } \right)} \right) \hfill \\ \end{gathered} \right]}^{\chi } {\text{d}}A \\ \end{aligned} $$

(40)

$$ \delta \Upsilon^{*\chi } = \int {\left[ {N^{T} \frac{{\partial w_{0} }}{\partial r}\frac{{\partial \delta w_{0} }}{\partial r} + \frac{{N^{T} }}{r}\frac{{\partial w_{0} }}{\partial r}\delta w_{0} + \frac{{N^{T} }}{{r^{2} }}\frac{{\partial w_{0} }}{\partial \theta }\frac{{\partial \delta w_{0} }}{\partial \theta }} \right]^{\chi } {\text{d}}A} , $$

(41)

where:

$$ \left\{ {I^{i} } \right\} = \int\limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\rho_{\chi } \left( z \right)\left\{ {z^{i} } \right\}{\text{d}}Z} ,\quad i = 0:2, $$

(42)

$$ \begin{aligned} \left\{ {N^{rr} ,M^{rr} } \right\}^{\chi } & = \int_{z} {\left\{ {\sigma^{rr} ,z\sigma^{rr} } \right\}^{\chi } } {\text{d}}z; \\ \left\{ {N^{\theta \theta } ,M^{\theta \theta } } \right\}^{\chi } & = \int_{z} {\left\{ {\sigma^{\theta \theta } ,z\sigma^{\theta \theta } } \right\}^{\chi } } {\text{d}}z;\, \\ \left\{ {N^{rz} ,M^{rz} ,Q^{rz} } \right\}^{\chi } & = \int_{z} {\left\{ {\sigma^{rz} ,z\sigma^{rz} ,z^{2} \sigma^{rz} } \right\}^{\chi } } {\text{d}}z; \\ \left\{ {N^{r\theta } ,M^{r\theta } ,Q^{r\theta } } \right\}^{\chi } & = \int_{z} {\left\{ {\sigma^{r\theta } ,z\sigma^{r\theta } ,z^{2} \sigma^{r\theta } } \right\}}^{\chi } {\text{d}}z; \\ \left\{ {N^{\theta z} ,M^{\theta z} ,Q^{\theta z} } \right\}^{\chi } & = \int_{z} {\left\{ {\sigma^{\theta z} ,z\sigma^{\theta z} ,z^{2} \sigma^{\theta z} } \right\}^{\chi } } {\text{d}}z. \\ \end{aligned} $$

(43)

Motion equation of the system can be achieved as follows:

$$ \delta u_{0}^{\chi } :\,\,\partial_{r} N_{\chi }^{rr} - \frac{{N_{\chi }^{\theta \theta } - N_{\chi }^{rr} }}{r} + \frac{1}{r}\partial_{\theta } N_{\chi }^{r\theta } = I_{\chi }^{0} \partial_{t}^{\left( 2 \right)} u_{0}^{\chi } + I_{\chi }^{1} \partial_{t}^{\left( 2 \right)} u_{1}^{\chi } , $$

(44)

$$ \delta v_{0}^{\chi } :\,\,\frac{1}{r}\partial_{\theta } N_{\chi }^{\theta \theta } + \frac{{2N_{\chi }^{r\theta } }}{r} + \partial_{r} N_{\chi }^{r\theta } = I_{\chi }^{0} \partial_{t}^{\left( 2 \right)} v_{0}^{\chi } + I_{\chi }^{1} \partial_{t}^{\left( 2 \right)} v_{1}^{\chi } , $$

(45)

$$ \delta w_{0}^{\chi } :\,\partial_{r} Q_{\chi }^{r} + \frac{1}{r}\partial_{\theta } Q_{\chi }^{\theta r} + \,\frac{1}{r}Q_{\chi }^{r} - N^{T} \partial_{r}^{\left( 2 \right)} w_{0}^{\chi } - \frac{{N^{T} }}{r}\partial_{r} w_{0}^{\chi } - \frac{{N^{T} }}{{r^{2} }}\partial_{\theta }^{\left( 2 \right)} w_{0}^{\chi } = I_{\chi }^{0} \partial_{t}^{\left( 2 \right)} w_{0}^{\chi } , $$

(46)

$$ \delta u_{1}^{\chi } :\,\partial_{r} M_{\chi }^{rr} - \frac{{M_{\chi }^{\theta \theta } - M_{\chi }^{rr} }}{r} + \frac{1}{r}\partial_{\theta } M_{\chi }^{r\theta } - Q_{\chi }^{r} = I_{\chi }^{1} \partial_{t}^{\left( 2 \right)} u_{0}^{\chi } + I_{\chi }^{2} \partial_{t}^{\left( 2 \right)} u_{1}^{\chi } , $$

(47)

$$ \delta v_{1}^{\chi } :\,\frac{1}{r}\partial_{\theta } M_{\chi }^{\theta \theta } + \frac{2}{r}M_{\chi }^{r\theta } + \partial_{\theta } M_{\chi }^{r\theta } - Q_{\chi }^{\theta } = I_{\chi }^{1} \partial_{t}^{\left( 2 \right)} v_{0}^{\chi } + I_{\chi }^{2} \partial_{t}^{\left( 2 \right)} v_{1}^{\chi } . $$

(48)

In addition, the general boundary conditions can be formulated as the following relations:

$$ \delta u_{0}^{\chi } = 0\quad {\text{or}}\quad N_{\chi }^{rr} n_{r} + \frac{1}{r}N_{\chi }^{r\theta } n_{\theta } = 0; $$

(49)

$$ \delta v_{0}^{\chi } = 0\quad {\text{or}}\quad N_{\chi }^{r\theta } n_{r} + \frac{1}{r}N_{\chi }^{\theta \theta } n_{\theta } = 0; $$

(50)

$$ \delta w_{0}^{\chi } = 0\quad {\text{or}}\quad Q_{\chi }^{r} n_{r} + \frac{{Q_{\chi }^{\theta } }}{r}n_{\theta } = 0; $$

(51)

$$ \delta u_{1}^{\chi } = 0\quad {\text{or}}\quad M_{\chi }^{rr} n_{r} + \frac{{M_{\chi }^{r\theta } }}{r}n_{\theta } = 0; $$

(52)

$$ \delta v_{1}^{\chi } = 0\quad {\text{or}}\quad M_{\chi }^{r\theta } n_{r} + \frac{{M_{\chi }^{\theta \theta } }}{r}n_{\theta } = 0. $$

(53)

Based on the compatibility conditions, have:

$$ u^{c} (z_{c} = - h_{c} /2) = u^{b} (z_{b} = h_{b} /2), $$

(54)

$$ v^{c} (z_{c} = - h_{c} /2) = v^{b} (z_{b} = h_{b} /2), $$

(55)

$$ w^{c} (z_{c} = - h_{c} /2) = w^{b} (z_{p} = h_{b} /2), $$

(56)

$$ w^{c} (z_{c} = - h_{c} /2) = w^{b} (z_{p} = h_{b} /2), $$

(57)

$$ u^{c} (z_{c} = h_{c} /2) = u^{t} (z_{t} = - h_{t} /2), $$

(58)

$$ v^{c} (z_{c} = h_{c} /2) = v^{t} (z_{t} = - h_{t} /2), $$

(59)

$$ w^{c} (z_{c} = h_{c} /2) = w^{t} (z_{t} = - h_{t} /2). $$

(60)

It should be noted that, according to the Eqs. (54–60), the unknown variables numbers are decreased from 15 to 9. Finally, by solving this 9 equations, the eigenvectors and eigenvalues of the structure can be achieved.