iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://unpaywall.org/10.1007/S00224-014-9591-3
On Minimum- and Maximum-Weight Minimum Spanning Trees with Neighborhoods | Theory of Computing Systems Skip to main content
Springer Nature Link
Log in

On Minimum- and Maximum-Weight Minimum Spanning Trees with Neighborhoods

  • Published:
Theory of Computing Systems Aims and scope Submit manuscript

Abstract

We study optimization problems for the Euclidean Minimum Spanning Tree (MST) problem on imprecise data. To model imprecision, we accept a set of disjoint disks in the plane as input. From each member of the set, one point must be selected, and the MST is computed over the set of selected points. We consider both minimizing and maximizing the weight of the MST over the input. The minimum weight version of the problem is known as the Minimum Spanning Tree with Neighborhoods (MSTN) problem, and the maximum weight version (max-MSTN) has not been studied previously to our knowledge. We provide deterministic and parameterized approximation algorithms for the max-MSTN problem, and a parameterized algorithm for the MSTN problem. Additionally, we present hardness of approximation proofs for both settings.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Notes

  1. For an informal discussion of sum-of-square-roots-hard problems, see [14].

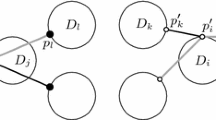
  2. Separability is similar in spirit to the notion of a well-separated pair; see [8]

  3. Note that the number of edges in the construction is a polynomial in the size of the input. Since all we need to determine is whether the weight of the solution is at least 0.34 units less than w tot, we can round the measure of the total weight to a number of bits that is logarithmic in the size of the input.

  4. If the Z D configurations were maintained, then the e-wire could be joined sub-optimally to the variable gadget with weight 5.5, since the assignment is not satisfying. However, a larger MST can be achieved by deviating from the Z D configuration in the variable gadget.

  5. Using this construction, pairs of disks of the gadget trivially intersect at a single point, which simplifies our analysis. To achieve strict disjointedness, the disks of the gadget may be contracted to have radius 1−γ so that the tangent point is now distance γ from the nearest point in the adjacent disks. Any path which uses the tangent point in our analysis will have less than 2γ units of additional weight on these shrunken disks, and there are fewer than n(8m + 6) disks, where n and m are the number of variables and clauses respectively. Choosing an appropriate value of γ so that 2γ n(8m + 6) ≪ 0.0735 achieves the same result as our simplified analysis.

  6. D i+2 may be more generally indexed as D i+2+4c , where there is a block of 4c disks in the variable gadget joined to the interior of the gadget in a truth configuration opposite of that of the neighboring disks in the variable gadget. This does not affect the analysis, it simply relocates the singleton disk. Recall that by Lemma 9, such singletons would exist rather than having three disks connected by a path to a single edge of the interior of the gadget.

  7. Note that the number of edges in the construction is a polynomial in the size of the input. Since all we need to determine is whether the weight of the solution is at least 0.0735 units greater than w tot, we can round the measure of the total weight to a number of bits logarithmic in the size of the input.

References

  1. Arkin, E., Hassin, R.: Approximation algorithms for the geometric covering salesman problem. Discret. Appl. Math. 55(3), 197–218 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  2. Arora, S.: Polynomial time approximation schemes for Euclidean traveling salesman and other geometric problems. J. ACM 45(5), 753–782 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  3. Bajaj, C.: Geometric optimization and computational complexity. Ph.D. thesis, Cornell University (1984)

  4. Bajaj, C.: The algebraic degree of geometric optimization problems. Discret. Comput. Geom. 3(1), 177–191 (1988)

    Article  MATH  MathSciNet  Google Scholar 

  5. de Berg, M., Gudmundsson, J., Katz, M., Levcopoulos, C., Overmars, M., van der Stappen, A.: TSP with neighborhoods of varying size. J. Algorithm. 57(1), 22–36 (2005)

    Article  MATH  Google Scholar 

  6. Biedl, T., Kaufmann, M.: Area-efficient static and incremental graph drawings In: Proceedings of the European Symposium on Algorithms, Lecture Notes in Computer Science, vol. 1284, pp. 37–52 (1997)

  7. Blömer, J.: Computing sums of radicals in polynomial time. In: Proceedings of the Symposium on Foundations of Computer Science (FOCS), pp. 670–677. IEEE Computer Society (1991)

  8. Callahan, P.B., Kosaraju, S.R.: A decomposition of multidimensional point sets with applications to k-nearest-neighbors and n-body potential fields. J. ACM 42(1), 67–90 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  9. Chambers, E., Erickson, A., Fekete, S., Lenchner, J., Sember, J., Venkatesh, S., Stege, U., Stolpner, S., Weibel, C., Whitesides, S.: Connectivity graphs of uncertainty regions In: Proceedings of the International Symposium on Algorithms and Computation (ISAAC), Lecture Notes in Computer Science, vol. 6507, pp. 434–445 (2010)

  10. Chou, C.C.: An efficient algorithm for relay placement in a ring sensor networks. Expert Syst. Appl. 37(7), 4830–4841 (2010)

    Article  Google Scholar 

  11. Dumitrescu, A., Mitchell, J.S.: Approximation algorithms for TSP with neighborhoods in the plane. J. Algorithm 48(1), 135–159 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  12. Durocher, S., Kirkpatrick, D.: The projection median of a set of points. Comput. Geom. 42(5), 364–375 (2009). Special Issue on the Canadian Conference on Computational Geometry (CCCG 2005 and CCCG 2006)

    Article  MATH  MathSciNet  Google Scholar 

  13. Erickson, J., (user J εffE): Sum-of-square-roots-hard problems? Theoretical Computer Science on StackExchange, http://cstheory.stackexchange.com/questions/4053/sum-of-square-roots-hard-problems (2011)

  14. Erlebach, T., Hoffmann, M., Krizanc, D., Mihalák, M., Raman, R.: Computing minimum spanning trees with uncertainty In: Proceedings of the Symposium on Theoretical Aspects of Computer Science (STACS), pp. 277–288 (2008)

  15. de Fermat, P.: Oeuvres de Fermat (Tome 1). Gauthier-Villars et Fils, Paris (1891)

    Google Scholar 

  16. Fiala, J., Kratochvíl, J., Proskurowski, A.: Systems of distant representatives. Discret. Appl. Math. 145(2), 306–316 (2005)

    Article  MATH  Google Scholar 

  17. Fischetti, M., Hamacher, H.W., Jørnsten, K., Maffioli, F.: Weighted k-cardinality trees: Complexity and polyhedral structure. Networks 24(1), 11–21 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  18. Graham, R.L., Hell, P.: On the history of the minimum spanning tree problem. IEEE Ann. Hist. Comput. 7(1), 43–57 (1985)

    Article  MATH  MathSciNet  Google Scholar 

  19. Jarník, V.: O jistém problému minimálním (About a certain minimal problem). Práca Moravské Prírodovedecké Spolecnosti 6, 57–63 (1930). (in Czech, German summary)

    Google Scholar 

  20. Lichtenstein, D.: Planar formulae and their uses. SIAM J. Comput. 11(2), 329–343 (1982)

    Article  MATH  MathSciNet  Google Scholar 

  21. Löffler, M., van Kreveld, M.: Largest and smallest convex hulls for imprecise points. Algorithmica 56(2), 235–269 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  22. Sekino, J.: n-ellipses and the minimum distance sum problem. Am. Math. Mon. 106(3), 193–202 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  23. Yang, Y.: On several geometric network design problems. Ph.D. thesis, State University of New York at Buffalo (2008)

  24. Yang, Y., Lin, M., Xu, J., Xie, Y.: Minimum spanning tree with neighborhoods In: Proceedings of Algorithmic Aspects in Information and Management (AAIM), Lecture Notes in Computer Science, vol. 4508, pp. 306–316 (2007)

Download references

Author information

Authors and Affiliations

  1. Dalhousie University, Halifax, Canada

    Reza Dorrigiv & Meng He

  2. University of Manitoba, Winnipeg, Canada

    Robert Fraser

  3. University of Waterloo, Waterloo, Canada

    Shahin Kamali & Alejandro López-Ortiz

  4. University of Tokyo, Tokyo, Japan

    Akitoshi Kawamura

  5. University of Concepción, Concepción, Chile

    Diego Seco

Authors
  1. Reza Dorrigiv
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Robert Fraser
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Meng He
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Shahin Kamali
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Akitoshi Kawamura
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Alejandro López-Ortiz
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Diego Seco
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Robert Fraser.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dorrigiv, R., Fraser, R., He, M. et al. On Minimum- and Maximum-Weight Minimum Spanning Trees with Neighborhoods. Theory Comput Syst 56, 220–250 (2015). https://doi.org/10.1007/s00224-014-9591-3

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00224-014-9591-3

Keywords

Search

Navigation