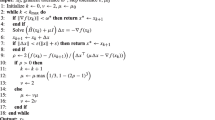iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://unpaywall.org/10.1007/BF02577874
A singular loop transformation framework based on non-singular matrices | International Journal of Parallel Programming Skip to main content
Springer Nature Link
Log in

A singular loop transformation framework based on non-singular matrices

  • Published:
International Journal of Parallel Programming Aims and scope Submit manuscript

Abstract

In this paper, we discuss a loop transformation framework that is based on integer non-singular matrices. The transformations included in this framework are called Λ-transformations and include permutation, skewing and reversal, as well as a transformation calledloop scaling. This framework is more general than existing ones; however, it is also more difficult to generate code in our framework. This paper shows how integer lattice theory can be used to generate efficient code. An added advantage of our framework over existing ones is that there is a simple completion algorithm which, given a partial transformation matrix, produces a full transformation matrix that satisfies all dependences. This completion procedure has applications in parallelization and in the generation of code for NUMA machines.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. D. Padua and M. Wolfe, Advanced compiler optimizations for supercomputers,Comm. of ACM,29(12):1184–1201 (December 1986).

    Article  Google Scholar 

  2. R. Allen and K. Kennedy, Automatic translation of FORTRAN programs to vector form.ACM Trans. on Programming Languages and Syst.,9(4):491–542 (October 1987).

    Article  MATH  Google Scholar 

  3. M. Wolfe,Optimizing Supercompilers for supercomputers, Pitman Publishing, London (1989).

    MATH  Google Scholar 

  4. U. Banerjee, Unimodular transformations of double loops,Proc. of the Workshop on Advances in Languages and Compilers for Parallel Processing, pp. 192–219 (August 1990).

  5. M. Wolf and M. Lam, A data locality optimizing algorithmProc. ACM SIGPLAN Conf. on Programming Language Design and Implementation, pp. 30–44 (June 1991).

  6. M. Wolf and M. Lam, A loop transformation theory and an algorithm to maximize parallelism,IEEE Trans. on Parallel and Distrib. Syst. (October 1991).

  7. W. Li and K. Pingali, Access Normalization: Loop restructuring for NUMA compilers,Proc. 5th Int'l Conf. on Archit. Support for Programming Languages and Oper. Syst. (October 1992).

  8. J. W. S. Cassels,An Introduction to the Geometry of Numbers, Berlin, Springer (1959).

    MATH  Google Scholar 

  9. A. Schrijver,Theory of Linear and Integer Programming, John Wiley and Sons (1986).

  10. G. B. Dantzig and B. C. Eaves, Fourier-motzkin elimination and its dual,J. of Combinatorial Theory(A),14:288–297 (1973).

    Article  MATH  MathSciNet  Google Scholar 

  11. C. Ancourt and F. Irigoin, Scanning polyhedra with DO loops,Third ACM Symp. on Principles and Practice of Parallel Programming, pp. 39–50 (April 1991).

  12. L. Lu, A unified framework for systematic loop transformations,3rd ACM SIGPLAN Symp. on Principles and Practice of Parallel Programming, pp. 28–38 (April 1991).

  13. K. Gallivan, W. Jalby, and D. Gannon, On the problem of optimizing data transfers for complex memory systems,Int'l. Conf. on Supercomputing, pp. 238–253 (1988).

  14. G. H. Golub and C. F. Van Loan,Matrix Computations, Johns Hopkins University Press (1989).

  15. L. Lamport, The parallel execution of do loops,Comm. of the ACM, pp. 83–93 (February 1974).

  16. M. Dowling, Optimal code parallelization using unimodular transformations,Parallel Computing,16:157–171 (1990).

    Article  MathSciNet  Google Scholar 

  17. J. Ramanujam, Non-unimodular transformations of nested loops,Proc. of Supercomputing (1992).

  18. M. Barnett and C. Lengauer, Loop parallelization and unimodularity, Technical Report ECS-LFCS-92-197, University of Edinburgh (1992).

  19. V. Sarkar and R. Thekkath, A general framework for iteration-reordering loop transformations,Proc. ACM SIGPLAN Conf. on Programming Language Design and Implementation (1992).

Download references

Author information

Authors and Affiliations

  1. Department of Computer Science, Cornell University, 14853, Ithaca, New York

    Wei Li & Keshav Pingali

Authors
  1. Wei Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Keshav Pingali
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

This work was supported by the Cornell Theory Center, NSF Presidential Young Investigator award #CCR-8958543. by NSF Grant #CCR-9008526, and by a grant from the Hewlett-Packard Company.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Li, W., Pingali, K. A singular loop transformation framework based on non-singular matrices. Int J Parallel Prog 22, 183–205 (1994). https://doi.org/10.1007/BF02577874

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02577874

Key Words

Search

Navigation