Abstract
Hash Proof Systems or Smooth Projective Hash Functions (SPHFs) are a form of implicit arguments introduced by Cramer and Shoup at Eurocrypt’02. They have found many applications since then, in particular for authenticated key exchange or honest-verifier zero-knowledge proofs. While they are relatively well understood in group settings, they seem painful to construct directly in the lattice setting.
Only one construction of an SPHF over lattices has been proposed in the standard model, by Katz and Vaikuntanathan at Asiacrypt’09. But this construction has an important drawback: it only works for an ad-hoc language of ciphertexts. Concretely, the corresponding decryption procedure needs to be tweaked, now requiring q many trapdoor inversion attempts, where q is the modulus of the underlying Learning With Errors (LWE) problem.
Using harmonic analysis, we explain the source of this limitation, and propose a way around it. We show how to construct SPHFs for standard languages of LWE ciphertexts, and explicit our construction over a tag-IND-CCA2 encryption scheme à la Micciancio-Peikert (Eurocrypt’12). We then improve our construction and our analysis in the case where the tag is known in advance or fixed (in the latter case, the scheme is only IND-CPA) with a super-polynomial modulus, to get a stronger type of SPHF, which was never achieved before for any language over lattices.
Finally, we conclude with applications of these SPHFs: password-based authenticated key exchange, honest-verifier zero-knowledge proofs, and a relaxed version of witness encryption.
O. Blazy—This work has been supported by the French ANR project ID-FIX (ANR-16-CE39-0004).
L. Ducas—This work has been supported by a Veni Grant from NWO.
W. Quach—Research supported in part by NSF grants CNS-1314722, CNS-1413964. This work was partly realized during an internship program at CWI.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Harmonic analysis is a powerful tool in geometry of numbers, especially in combination with Gaussian measure, which has lead to important progress on transference theory [3]. Those tools also played a crucial role for the foundation of lattice-based cryptography, being at the heart of proofs of worst-case hardness for lattice problems, such as the Short Integer Solution problem (SIS) and the Learning with Errors (LWE) problem [14, 28, 29]. Later, security proofs relied on a few convenient lemmas in a black-box manner, and for most applications this was sufficient: lattice-based cryptography quickly caught up with pairing-based cryptography, for example with the constructions of (Hierarchical) Identity Based Encryption’s [9, 14, 27] and beyond [8, 15, 16].
There nevertheless remains one primitive for which lattice-based cryptography is still far behind: Hash Proof Systems or Smooth Projective Hash Functions (SPHFs) [11]. Beyond the original Chosen-Ciphertext secure encryption scheme of Cramer and Shoup [10], SPHFs give rise to generalized classes of Authenticated Key Exchange (Password-based, Language-based, ...) [2, 4, 13, 23]. They also have been used in Oblivious Transfer [18, 21], One-Time Relatively-Sound Non-Interactive Zero-Knowledge Arguments [20], and Zero-Knowledge Arguments [5].
An SPHF can be seen as an implicit (designated-verifier) zero-knowledge proof for a language. The most useful languages for SPHFs are the languages of ciphertexts of a given plaintext M.
To our knowledge, there is only one construction of SPHF for a lattice-based encryption scheme in the standard model, given by Katz and Vaikuntanathan [22]. There is also a subsequent work by Zhang and Yu who propose an interesting new lattice-based SPHF in [30]. But the language of the SPHF relies on simulation-sound non-interactive zero-knowledge proofs which we do not know how to construct just under lattice-based assumptions without random oracle.
Unfortunately, the only standard-model lattice-based SPHF construction in [22] has a main drawback: the language of the SPHF is not simply defined as the set of valid standard LWE ciphertexts. Naturally, the set of valid ciphertexts of 0 should correspond to the set of ciphertexts close to the lattice defined by the public key. Instead, their language includes all the ciphertexts \(\varvec{c}\) such that at least one integer multiple is close to the public lattice. This makes the decryption procedure very costly (about q trapdoor inversions), and forbids the use of super-polynomial modulus q. This limitation is a serious obstacle to the construction of a stronger type of SPHF introduced in [23], namely word-independent SPHF for which the projection key (which can be seen as the public key of the SPHF) does not depend on the ciphertext \(\varvec{c}\) (a.k.a., word in the SPHF terminology).Footnote 1
This strongly contrasts with SPHFs in a group-based setting, which can handle classical ElGamal or Cramer-Shoup encryption schemes—for example [11, 13]—without any modification of the decryption procedure. This is a technical hassle to carry when building on top of such an SPHF.
We therefore view as an important question to determine whether this caveat is inherent to lattice-based SPHFs, or if it can be overcome. We shall find an answer by re-introducing some harmonic analysis.
Contributions. Our main contribution consists in constructing SPHFs for standard lattice-based encryption schemes. We provide general theorems to ease the proofs of correctness and security (a.k.a., smoothness or universality) of SPHFs over standard lattice-based encryption schemes. We detail two particular instantiations: one over an IND-CCA2 encryption scheme à la Micciancio-Peikert [27], and one over an IND-CPA restriction of the same scheme. While the second instantiation is over a simpler language, it is a word-independent SPHF. To our knowledge, this is the first word-independent SPHF over any lattice-based language. We remark that while Zhang and Yu construct an interesting approximate word-independent SPHF over a lattice-based language in [30], its correctness is only approximate contrary to our SPHF; and its language also relies on simulation-sound non-interactive zero-knowledge proofs, which we do not know how to construct just from lattice assumptions in the standard model.
As with many zero-knowledge-type primitives in the lattice setting [24, 25] and as with the SPHFs of [22] and of [30], there is a gap between the correctness property and the smoothness property. Concretely, smoothness holds for ciphertexts which do not decrypt to a given message, while correctness holds only for honestly generated ciphertexts. However, contrary to [22], we use a standard encryption scheme and do not need to tweak the decryption procedure nor the language. We thus avoid the main caveat of the latter paper.
Applications. Having built these new SPHFs, we can now proceed with several applications showing that the gap between smoothness (or universality) and correctness is not an issue in most cases. We start by proposing an efficient password-authenticated key exchange (PAKE) scheme in three flows. We do so by plugging our first SPHF in the framework from [22]. Following the GK-PAKE construction from [1] which is an improvement of the Groce-Katz framework [17, 19], we also obtain a PAKE in two flows over lattices in the standard model. Finally, using our word-independent SPHF together with simulation-sound non-interactive zero-knowledge proofs (SS-NIZK), by following [23], we obtain a one-round PAKE.
Compared to the recent work of Zhang and Yu [30], which proposes the first two-round lattice-based PAKE assuming in addition SS-NIZK, our two-round PAKE does not require SS-NIZK. While there exist very efficient SS-NIZKs in the random oracle model for the languages considered by Zhang and Yu, constructing SS-NIZK in the standard model under a lattice-based assumption remains an important open problem. Our two-round PAKE is thus the first two-round PAKE solely based on lattice assumptions in the standard model. In addition, our one-round PAKE assuming LWE and SS-NIZK is the first one-round PAKE in this setting and closes an open problem of [30].
In addition to PAKE, we also show how to construct honest-verifier zero-knowledge proofs for any NP language from lattice-based SPHF. We conclude by showing a relaxed version of witness encryption for some lattice-based languages. Witness encryption is a very recent primitive introduced in [12] which enables a user to encrypt a message to a given word of some NP language. The message can be decrypted using a witness for the word.
Technical Overview. Let us now give a technical overview of our main contribution, namely the constructions of new lattice-based SPHFs. We focus on the language of dual-Regev ciphertexts \(\varvec{c}\) of 0: \(\varvec{c} = \varvec{A} \varvec{s} + \varvec{e} \in \mathbb {Z}_q^m\), where \(\varvec{A} \in \mathbb {Z}_q^{m \times n}\) is a public matrix, while \(\varvec{s} \in \mathbb {Z}_q^n\) and \(\varvec{e} \in \mathbb {Z}_q^m\) correspond to the randomness of the ciphertext. The vector \(\varvec{e}\) is supposed to be small, i.e., \(\varvec{c}\) is close to the q-ary lattice \(\varLambda \) generated by \(\varvec{A}\).
Intuitively, an SPHF allows a prover knowing \(\varvec{s}\) and \(\varvec{e}\) to prove to a verifier that \(\varvec{c}\) is indeed a ciphertext of 0. The naive and natural construction works as follows.Footnote 2 The verifier generates a small random vector \(\mathsf {hk}= \varvec{h} \in \mathbb {Z}_q^m\) called a hashing key. It then “hashes” the ciphertext into a hash value \(\mathsf {H}= R(\langle \varvec{h}, \varvec{c} \rangle ) \in {\{0,1\}}\), where R is a rounding function from \(\mathbb {Z}_q\) to \({\{0,1\}}\) to be chosen later. The verifier also derives from \(\mathsf {hk}= \varvec{h}\), a projection key \(\mathsf {hp}= \varvec{p} = \varvec{A}^t \varvec{h} \in \mathbb {Z}_q^n\) that it sends to the prover. The prover can then compute the projected hash value \(\mathsf {pH}= R(\langle \varvec{p}, \varvec{s} \rangle )\) from the projection key \(\varvec{p}\) and the randomness of the ciphertext \(\varvec{s}\) and \(\varvec{e}\). It can send this projected hash value to the verifier which will accept the proof, if \(\mathsf {pH}\) matches its hash value \(\mathsf {H}\).
We remark that if indeed \(\varvec{c} = \varvec{A} \varvec{s} + \varvec{e}\) with \(\varvec{e}\) small enough (recall that \(\varvec{h}\) is small as well):
Hence, if R is carefully chosen, we can ensure that with high probability (e.g., at least 3/4), \(\mathsf {H}= \mathsf {pH}\), and the verifier will accept the prover’s “proof.” This property is called approximate correctness. An SPHF also needs to satisfy a security property to be useful, called smoothness or universality, which ensures that if \(\varvec{c}\) is far from the q-ary lattice \(\varLambda \) generated by \(\varvec{A}\) (in particular if it is an encryption of 1), then given the projection key \(\varvec{p}\) (and \(\varvec{A}\) and \(\varvec{c}\)), the prover cannot guess the hash value \(\mathsf {H}\) with probability more than \(1/2 + {{\mathrm{negl}}}(n)\). In [22], Katz and Vaikuntanathan argued universality for ciphertexts \(\varvec{c}\), for which every multiple of \(\varvec{c}\) is far from the lattice \(\varLambda \). To be useful in their PAKE application, the decryption procedure of the encryption scheme therefore needs to be tweaked to try to decrypt not only the ciphertext itself but also all its multiples. In particular, their construction cannot work with super-polynomial moduli.
The question we wish to answer is whether universality holds without this tweak. In other words, is the condition that \(j\varvec{c}\) is far from \(\varLambda \) for all \(j \ne 0\) truly necessary or is it is an artifact of the proof? To approach this question, let us discuss two case studies.
Two case studies. Let us first take a look at the special case where q is even, and where \(\varvec{c}\) is a perfect encryption of 1: \(\varvec{c} = \varvec{A} \varvec{s} + (0, \dots , 0, q/2)^t\) for some \(\varvec{s}\in \mathbb {Z}_q^n\). We observe that
where \(h_m\) is the last coordinate of \(\varvec{h}\). In particular, the distribution of \(\langle \varvec{h}, \varvec{c} \rangle \), when \(\varvec{h}\) is drawn from a discrete Gaussian (over \(\mathbb {Z}^m\)), conditioned on \(\varvec{A}, \varvec{c}\) and \(\varvec{A}^t \varvec{h} = \varvec{p}\), is concentrated on merely 2 values out of q and is therefore far from uniform.
Yet, assuming the discrete Gaussian has large enough parameter (more precisely, twice as large as the smoothing parameter of \(\mathbb {Z}\)), we note that \(h_m\) is close to uniform modulo 2. In that case we observe that while \(\langle \varvec{h}, \varvec{c} \rangle \) is not itself uniform, the rounding \(R(\langle \varvec{h}, \varvec{c} \rangle )\) is close to uniform when choosing the typical rounding function \(R: x \in \mathbb {Z}_q \mapsto \lfloor 2x/q \rceil \mod 2\), regardless of the value of \(\langle \varvec{p}, \varvec{s} \rangle \). So it seems that the rounding function does not only help in ensuring approximate correctness, but it can also improve universality of the scheme as well!
Unfortunately, we cannot always expect universality from this trick. Now assume that q is divisible by 3, and set \(\varvec{c} = \varvec{A} \varvec{s} + (0, \dots , 0, q/3)^t\). This time,
is (almost) uniformly distributed over three values, separated by q/3. In particular \(R(\langle \varvec{h}, \varvec{c} \rangle )\) will take one value with probability (roughly) 1/3, and the other value with probability (roughly) 2/3. Despite imperfect universality, this still guarantees some entropy in \(\mathsf {Hash}(\varvec{h}, \varvec{A}, \varvec{c})\) knowing \(\varvec{A}, \varvec{c}\), and \(\varvec{p}\).
Harmonic analysis. The core of our work consists in using harmonic analysis to better understand the caveat of [22], namely that universality is only proven when all the multiples of the ciphertext are far from the lattice. For that, we extend the rounding function R to a q-periodic signal \(\mathbb R \rightarrow \mathbb R\).
We proceed to a general analysis (Theorem 3.1), which shows that universality holds for ciphertexts \(\varvec{c}\) such that its multiples \(j \varvec{c}\) are far away from the lattice \(\varLambda \), for all non-zero integers j corresponding to non-zero real harmonics of the rounding signal R.
This unravels the causes of the caveat in [22]: the weight of the j-th harmonic of the naive rounding function \(R:x \in \mathbb {Z}_q \mapsto \lfloor 2x/q \rceil \bmod 2\) (seen as a q-periodic signal, as in Fig. 1a) is as large as \(\varTheta (1/j)\) for odd integers j.
First solution (Universality, Approximate Correctness, Sect. 3 ). Having identified the source of the caveat, it becomes clear how to repair it: the rounding should be randomized, with a weight signal for which only the first harmonic is non-zero (in addition to the average), namely with a pure cosine weight:
This choice ensures universality as soon as just \(1 \cdot \varvec{c} = \varvec{c}\) is far from the lattice \(\varLambda \) (Corollary 3.2 and Theorem 3.4).
This solution nevertheless only provides approximate correctness (correctness holds with probability \(3/4 +o(1)\), see Lemma 3.3), which is also problematic for some applications. This can be solved using correctness amplification via error-correcting codes, but at the price of preventing the resulting SPHF to be word-independent.
Second solution (Imperfect Universality, Statistical Correctness, Sect. 4 ). In our second instantiation, we therefore proceed to construct an almost-square rounding function (see Fig. 1d, \(\odot \) denotes the convolution operator), which offers statistical correctnessFootnote 3 and imperfect universality (namely the probability that a prover knowing only \(\mathsf {hp}= \varvec{p}\) can guess the hash value \(\mathsf {H}\) is at most \(1/3 + o(1)\), as proved in Theorem 4.5). This instantiation requires a more subtle analysis, taking account of destructive interferences.
We can then amplify universality to get statistical universality (i.e., the above probability of guessing is at most \(1/2 + {{\mathrm{negl}}}(n)\) as in our first solution) while keeping a statistical correctness. Contrary to the correctness amplification, this transformation preserves the independence of the projection key from the ciphertext. In particular, if the ciphertexts are from an IND-CPA scheme such as dual-Regev, then we get the first word-independent SPHF over a lattice-based language.
We remark that our word-independent SPHF uses a super-polynomial modulus q, to get statistical correctness. It seems hard to construct such an SPHF for a polynomial modulus, as a word-independent SPHF for an IND-CPA encryption scheme directly yields a one-round key exchange (where each party sends a ciphertext of 0 and a projection key, and where the resulting session key is the xor of the two corresponding hash values) and we do not know of any lattice-based one-round key exchange using a polynomial modulus.
Open Question. We see as the main open question to extend our techniques to their full extent in the ring-setting. More precisely, our SPHF only produces one-bit hashes, and is easily extended to the ring-setting still asking with 1-bit hash values. This requires costly repetitions for applications, and one would hope that a ring setting variant could directly produce \(\varTheta (n)\)-bit hash values.
Another important open question is to understand whether our techniques can further be refined to construct lattice-based IND-CCA encryption schemes without trapdoor, using ideas from the Cramer-Shoup encryption scheme [10, 11] for example.
Road Map. We start by some preliminaries on lattices and SPHFs in Sect. 2. In particular, we define several variants of lattice-based (approximate) SPHFs (in particular universal bit-PHFs) and formally show various transformations which were only implicit in [22]. We also define the IND-CCA2 encryption scheme “à la Micciancio-Peikert” we will be using. In Sect. 3, we then show step-by-step how to construct an SPHF for IND-CCA2 ciphertexts à la Micciancio-Peikert and how to avoid the caveat of the construction of [22]. In Sect. 4, we construct a word-independent SPHF for ciphertexts under an IND-CPA scheme à la Micciancio-Peikert, when the modulus is super-polynomial. In Sect. 5, we conclude by exhibiting several applications.
Figure 2 summarizes our results and the paper road map. All the notions in this figure are formally defined in Sect. 2.
2 Preliminaries
2.1 Notations
The security parameter is denoted n. The notation \({{\mathrm{negl}}}(n)\) denotes any function f such that \(f(n) = n^{-\omega (1)}\). For a probabilistic algorithm \(\mathsf {alg}(\mathsf {inputs})\), we may explicit the randomness it uses with the notation \(\mathsf {alg}(\mathsf {inputs} \, ; \, \mathsf {coins})\), otherwise the random coins are implicitly fresh.
Column vectors will be denoted by bold lower-case letters, e.g., \(\varvec{x}\), and matrices will be denoted by bold upper-case letters, e.g., \(\varvec{A}\). If \(\varvec{x}\) is vector and \(\varvec{A}\) is a matrix, \(\varvec{x}^t\) and \(\varvec{A}^t\) will denote their transpose. We use \([\varvec{A} | \varvec{B}]\) for the horizontal concatenation of matrices, and \([\varvec{A} \,;\, \varvec{B}] = [\varvec{A}^t | \varvec{B}^t]^t\) for the vertical concatenation. For \(\varvec{x} \in \mathbb {R}^m, \Vert \varvec{x}\Vert \) will denote the canonical euclidean norm of \(\varvec{x}\). We will use \(\mathcal {B}\) to denote the euclidean ball of radius 1, where, unless specifically stated otherwise, the ball is m-dimensional. If \(\varvec{x}, \varvec{y} \in \mathbb {R}^m, \langle \varvec{x}, \varvec{y} \rangle \) will denote their canonical inner product, and \(d(\varvec{x}, \varvec{y}) = \Vert \varvec{x} - \varvec{y} \Vert \) their distance. If \(E \subset \mathbb {R}^m\) is countable and discrete, we will denote \(d(\varvec{x}, E) = \min _{\varvec{y} \in E} d(\varvec{x}, \varvec{y})\). For a function \(f :E\rightarrow \mathbb {C}\) or \(f :E\rightarrow \mathbb {R}, f(E)\) will denote the sum \(\sum _{\varvec{x} \in E} f(x)\). For \(a,b \in \mathbb R\),  will denote the closed real interval with endpoints a and \(b, \lfloor a \rfloor , \lceil a \rceil \), and \(\lfloor a \rceil \) will respectively denote the largest integer smaller than a, the smallest integer greater than a, and the closest integer to a (the largest one if there are two). The xor of two bit strings \(a,b \in {\{0,1\}}^k\) is denoted by \(a \oplus b\). The cardinal of a finite set S is denoted |S|.
will denote the closed real interval with endpoints a and \(b, \lfloor a \rfloor , \lceil a \rceil \), and \(\lfloor a \rceil \) will respectively denote the largest integer smaller than a, the smallest integer greater than a, and the closest integer to a (the largest one if there are two). The xor of two bit strings \(a,b \in {\{0,1\}}^k\) is denoted by \(a \oplus b\). The cardinal of a finite set S is denoted |S|.
The modulus \(q \in \mathbb {Z}\) will be taken as an odd prime, for simplicity.
2.2 Lattices and Gaussians
Lattices. An m-dimensional lattice \(\varLambda \) is a discrete subgroup of \(\mathbb {R}^m\). Equivalently, \(\varLambda \) is a lattice if it can be written  where \(n \le m\), for some \(\varvec{B} \in \mathbb {R}^{m\times n}\), where the columns of \(\varvec{B}\) are linearly independent. In that case, \(\varvec{B}\) is called a basis of \(\varLambda \). Then, we define the determinant of \(\varLambda \) as \(\det (\varLambda ) = \sqrt{\det (\varvec{B}^t \varvec{B})}\), which does not depend on the choice of the basis \(\varvec{B}\).
where \(n \le m\), for some \(\varvec{B} \in \mathbb {R}^{m\times n}\), where the columns of \(\varvec{B}\) are linearly independent. In that case, \(\varvec{B}\) is called a basis of \(\varLambda \). Then, we define the determinant of \(\varLambda \) as \(\det (\varLambda ) = \sqrt{\det (\varvec{B}^t \varvec{B})}\), which does not depend on the choice of the basis \(\varvec{B}\).
We define the dual lattice of \(\varLambda \) as

Recall the identity \({(\varLambda ^*)}^* = \varLambda \). Given \(\varvec{A} \in \mathbb {Z}_q^{m \times n}\) where \(m \ge n\), and modulus \(q \ge 2\), we define the following q-ary lattices:

Note that up to a scaling factor, \(\varLambda (\varvec{A})\) and \(\varLambda ^\bot (\varvec{A})\) are dual of each other: \(\varLambda (\varvec{A}) = q \cdot \varLambda ^\bot (\varvec{A})^*\). For a syndrome \(\varvec{p} \in \mathbb {Z}_q^n\), we define the coset of \(\varLambda ^\bot (\varvec{A})\):

When there is no confusion about which matrix \(\varvec{A}\) is used, we will simply denote these lattices \(\varLambda , \varLambda ^\bot \), and \(\varLambda ^\bot _{\varvec{p}}\) respectively.
Gaussians. If \(s>0\) and \(\varvec{c} \in \mathbb {R}^m\), we define the Gaussian weight function on \(\mathbb {R}^m\) as
Similarly, if \(\varLambda \) is an m-dimensional lattice, we define the discrete Gaussian distribution over \(\varLambda \), of parameter s and centered in \(\varvec{c}\) by:
When \(\varvec{c} = \varvec{0}\), we will simply write \(\rho _s\) and \(D_{\varLambda ,s}\). We recall the tail-bound of Banaszczyk for discrete Gaussians:
Lemma 2.1
([3, Lemma 1.5], as stated in [28, Lemma 2.10]). For any \(c > 1/\sqrt{2\pi }, m\)-dimensional lattice \(\varLambda \) and any vector \(\varvec{v} \in \mathbb R^m\):
where \(C = c \sqrt{2 \pi e} \cdot e^{-\pi c^2} < 1\).
An important quantity associated to a lattice is its smoothing parameter, introduced by Micciancio and Regev [28]:
Definition 2.2
(Smoothing parameter [28]). For \(\epsilon > 0\), the smoothing parameter of a lattice \(\varLambda \), denoted \(\eta _\epsilon (\varLambda )\), is the smallest \(s>0\) such that \(\rho _{1/s}(\varLambda ^* \setminus \{0 \}) \le \epsilon \).
The following lemma states that if the parameter of the discrete Gaussian is above the smoothing parameter of the lattice, then the Gaussian weight of the cosets of \(\varLambda \) are essentially the same:
Lemma 2.3
[29, Claim 3.8]. For any lattice \(\varLambda \subset \mathbb R^m, \varvec{c} \in \mathbb {R}^m\), and \(s \ge \eta _\epsilon (\varLambda )\):
The smoothing parameter of the dual of a random q-ary lattice can be controlled using the following:
Lemma 2.4
(Corollary of [27, Lemma 2.4]). Fix parameters n, q a prime, and \(m \ge \varTheta (n\log q)\). Let \(\epsilon \ge 2^{-O(n)}\) and \(s > 2\eta _\epsilon (\mathbb {Z}^m)\). Fix \(0 < \delta \le 1\). Then, for \(\varvec{A}\) uniformly random in \(\mathbb {Z}_q^{m\times n}\), we have \(s \ge \eta _{2\epsilon / \delta }(\varLambda ^\bot (\varvec{A}))\) except with probability at most \(\delta \) over the choice of \(\varvec{A}\).
To instantiate the above, we recall the smoothing parameter of \(\mathbb {Z}^m\).
Lemma 2.5
(Corollary of [28, Lemma 3.3]). For all integer \(m\ge 1, \epsilon \in (0,1/2)\), the smoothing parameter of \(\mathbb {Z}^m\) satisfies \(\eta _\epsilon (\mathbb {Z}^m) \le C\sqrt{\log (m / \epsilon )}\) for some universal constant \(C>0\).
Harmonic analysis. Let us recall the exponential basis of periodic functions and their vectorial analogues:
The Fourier transform of \(f : \mathbb {R}^m \rightarrow \mathbb {C}\) is defined by:
The Fourier transform of the Gaussian weight function \(\rho _s\) is \(\widehat{\rho _s} = s^m \rho _{1/s}\). Recall the time-shift-phase-shift identity: if \(g(\varvec{x}) = f(\varvec{x})e_{\varvec{z}}(\varvec{x})\) for some \(\varvec{z} \in \mathbb {R}^m\), then \(\hat{g}(\varvec{\xi }) = \hat{f}(\varvec{\xi } - \varvec{z})\). Similarly, if \(g(\varvec{x}) = f(\varvec{x} + \varvec{t})\) for some \(\varvec{t} \in \mathbb {R}^m\), then \(\hat{g}(\varvec{\xi }) = \hat{f}(\varvec{\xi }) e_{\varvec{t}}(\varvec{\xi })\). For two functions \(f,g:\mathbb {R}^m \rightarrow \mathbb {C}\), we will denote by \(f \odot g\) their convolution product:
The Fourier transform turns convolutions into pointwise products, and conversely:
Finally, let us recall the Poisson summation formula:
Lemma 2.6
(Poisson summation formula). For any lattice \(\varLambda \) and \(f{:}\,\mathbb {R}^m \!\rightarrow \! \mathbb {C}\), we have \(f(\varLambda ) = \det (\varLambda ^*) \hat{f}(\varLambda ^*)\).
Learning with Errors
Definition 2.7
(Learning with Errors (LWE)). Let \(q \ge 2\), and \(\chi \) be a distribution over \(\mathbb {Z}\). The Learning with Errors problem LWE\(_{\chi , q}\) consists in, given polynomially many samples, distinguishing the two following distributions:
-
\((\varvec{a}, \langle \varvec{a}, \varvec{s} \rangle + e)\), where \(\varvec{a}\) is uniform in \(\mathbb {Z}_q^n\),
 , and \(\varvec{s} \in \mathbb {Z}_q^n\) is a fixed secret chosen uniformly,
, and \(\varvec{s} \in \mathbb {Z}_q^n\) is a fixed secret chosen uniformly, -
\((\varvec{a}, b)\), where \(\varvec{a}\) is uniform in \(\mathbb {Z}_q^n\), and b is uniform in \(\mathbb {Z}_q\).
In [29], Regev showed that for \(\chi = D_{\mathbb {Z}, \sigma }\), for any \(\sigma \ge 2 \sqrt{n}\), and q such that \(q/\sigma = {{\mathrm{poly}}}(n)\), LWE\(_{\chi , q}\) is at least as hard as solving worst-case SIVP for polynomial approximation factors.
Trapdoor for LWE. Throughout this paper, we will use the trapdoors introduced in [27] to build our public matrix \(\varvec{A}\). Define \(g_{\varvec{A}}(\varvec{s}, \varvec{e}) = \varvec{A} \varvec{s} + \varvec{e}\), let \(\varvec{G}^t = \varvec{I}_n \otimes \varvec{g}^t\), where \(\varvec{g}^t = [1,2,\dots , 2^{k} ] \) and \(k = \lceil \log q \rceil -1\), and let \(\varvec{H} \in \mathbb {Z}_q^{n\times n}\) be invertible.
Lemma 2.8
[27, Theorems 5.1 and 5.4]. There exist two PPT algorithms \(\mathsf {TrapGen}\) and \(g^{-1}_{(\cdot )}\) with the following properties assuming \(q \ge 2\) and \(m \ge \varTheta (n \log q)\):
-
\(\mathsf {TrapGen}(1^n,1^m,q)\) outputs \((\varvec{T}, \varvec{A}_0)\), where the distribution of the matrix \(\varvec{A}_0\) is at negligible statistical distance from uniform in \(\mathbb {Z}_q^{m\times n}\), and such that \(\varvec{T} \varvec{A}_0 = \varvec{0}\), where \(s_1(\varvec{T}) \le O(\sqrt{m})\) and where \(s_1(\varvec{T})\) is the operator norm of \(\varvec{T}\), which is defined as \(\max _{\varvec{x} \ne 0} \Vert \varvec{T} \varvec{x}\Vert / \Vert \varvec{x}\Vert \).Footnote 4
-
Let
 . Let \(\varvec{A}_{\varvec{H}} = \varvec{A}_0 + [\varvec{0} \,; \, \varvec{G} \varvec{H}]\) for some invertible matrix \(\varvec{H}\) called a tag. Then, we have \(\varvec{T} \varvec{A}_{\varvec{H}} = \varvec{G} \varvec{H}\). Furthermore, if \(\varvec{x} \in \mathbb {Z}_q^m\) can be written as \(\varvec{A}_{\varvec{H}} \varvec{s} + \varvec{e}\) where
. Let \(\varvec{A}_{\varvec{H}} = \varvec{A}_0 + [\varvec{0} \,; \, \varvec{G} \varvec{H}]\) for some invertible matrix \(\varvec{H}\) called a tag. Then, we have \(\varvec{T} \varvec{A}_{\varvec{H}} = \varvec{G} \varvec{H}\). Furthermore, if \(\varvec{x} \in \mathbb {Z}_q^m\) can be written as \(\varvec{A}_{\varvec{H}} \varvec{s} + \varvec{e}\) where 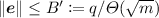 , then \(g_{\varvec{ A_{\varvec{H}}}}^{-1}(\varvec{T}, \varvec{x}, \varvec{H})\) outputs \((\varvec{s},\varvec{e})\).
, then \(g_{\varvec{ A_{\varvec{H}}}}^{-1}(\varvec{T}, \varvec{x}, \varvec{H})\) outputs \((\varvec{s},\varvec{e})\).
More precisely, to sample \((\varvec{T}, \varvec{A}_0)\) with \(\mathsf {TrapGen}\), we sample a uniform \(\varvec{\bar{A}} \in \mathbb {Z}_q^{\bar{m} \times n}\) where \(\bar{m} = m - nk = \varTheta (n\log q)\), and some  , where the distribution \(\mathcal {D}^{nk \times \bar{m}}\) assigns probability 1/2 to 0, and 1/4 to \({\pm }1\). We output \(\varvec{T} = [ -\varvec{R} \,| \, \varvec{I}_{nk} ]\) along with \(\varvec{A}_0 = [ \varvec{\bar{A}} \,;\, \varvec{R} \varvec{\bar{A}}]\). Then, given a tag \(\varvec{H}\), we have: \(\varvec{T} (\varvec{A}_0 + [\varvec{0} \,; \, \varvec{G} \varvec{H}]) \!=\! \varvec{G} \varvec{H}\).
, where the distribution \(\mathcal {D}^{nk \times \bar{m}}\) assigns probability 1/2 to 0, and 1/4 to \({\pm }1\). We output \(\varvec{T} = [ -\varvec{R} \,| \, \varvec{I}_{nk} ]\) along with \(\varvec{A}_0 = [ \varvec{\bar{A}} \,;\, \varvec{R} \varvec{\bar{A}}]\). Then, given a tag \(\varvec{H}\), we have: \(\varvec{T} (\varvec{A}_0 + [\varvec{0} \,; \, \varvec{G} \varvec{H}]) \!=\! \varvec{G} \varvec{H}\).
Tag-IND-CCA2 LWE Encryption à la Micciancio-Peikert. For our applications, we will need a (labelled) encryption scheme that is IND-CCA2. This can be built generically and efficiently from a tag-IND-CCA2 encryption scheme. The formal definitions and the latter transformation are recalled in the full version [6]. Below, we describe a simplified variant of the scheme of [27, Sect. 6.3].
For this scheme, we assume q to be an odd prime. We set an encoding function for messages \(\mathsf {Encode}(\mu \in \{0,1\}) = \mu \cdot (0, \dots 0, \lceil q/2 \rceil )^t\). Note that \(2 \cdot \mathsf {Encode}(\mu ) = (0, \dots , 0, \mu )^t \bmod q\).
Let \(\mathcal {R}\) be a ring with a subset \(\mathcal {U} \subset \mathcal {R^\times }\) of invertible elements, of size \(2^n\), and with the unit differences property: if \(u_1 \ne u_2 \in \mathcal {U}\), then \(u_1 - u_2\) is invertible in \(\mathcal {R}\). Let h be an injective ring homomorphism from \(\mathcal {R}\) to \(\mathbb {Z}_q^{n\times n}\) (see [27, Sects. 6.1 and 6.3] for an explicit construction). Note that if \(u_1 \ne u_2 \in \mathcal {U}\), then \(h(u_1 - u_2)\) is invertible, and thus an appropriate tag \(H = h(u_1-u_2)\) for the trapdoor.
Let  . The public encryption key is \(\mathsf {ek}= \varvec{A}_0\), and the secret decryption key is \(\mathsf {dk}= \varvec{T}\).
. The public encryption key is \(\mathsf {ek}= \varvec{A}_0\), and the secret decryption key is \(\mathsf {dk}= \varvec{T}\).
-
\(\mathsf {Encrypt}(\mathsf {ek}= \varvec{A}_0,\; u\in \mathcal U,\; \mu \in \{0,1\})\) encrypts the message \(\mu \) under the public key \(\mathsf {ek}\) and for the tag u, as follows: Let \(\varvec{A}_u = \varvec{A}_0 + [\varvec{0} \,;\, \varvec{G} h(u)]\). Pick \(\varvec{s} \in \mathbb {Z}_q^n\),
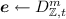 where \(t = \sigma \sqrt{m} \cdot \omega (\sqrt{\log n})\). Restart if \(\Vert \varvec{e}\Vert > B\), where
where \(t = \sigma \sqrt{m} \cdot \omega (\sqrt{\log n})\). Restart if \(\Vert \varvec{e}\Vert > B\), where  .Footnote 5 Output the ciphertext: $$\begin{aligned} \varvec{c} = \varvec{A}_u \varvec{s} + \varvec{e} + \mathsf {Encode}(\mu ) \bmod q . \end{aligned}$$
.Footnote 5 Output the ciphertext: $$\begin{aligned} \varvec{c} = \varvec{A}_u \varvec{s} + \varvec{e} + \mathsf {Encode}(\mu ) \bmod q . \end{aligned}$$ -
\(\mathsf {Decrypt}(\mathsf {dk}= \varvec{T},\; u\in \mathcal U,\; \varvec{c} \in \mathbb {Z}_q^m)\) decrypts the ciphertext \(\varvec{c}\) for the tag u using the decryption key \(\mathsf {dk}\) as follows: OutputFootnote 6
$$\begin{aligned} {\left\{ \begin{array}{ll} \mu &{}\text {if } g^{-1}_{\varvec{A}_u}(\varvec{T}, 2\varvec{c}, h(u)) = 2\varvec{e} + (0, \dots ,0 , \mu ) \text { where } \varvec{e} \in \mathbb {Z}^m \text { and } \Vert \varvec{e}\Vert \le B' , \\ \bot &{}\text {otherwise.} \end{array}\right. } \end{aligned}$$
Since \(\lceil q/2 \rceil \) is the inverse of \(2 \bmod q\), we have:

Suppose that \(m \ge \varTheta (n\log q)\). Note that \(d(\mathsf {Encode}(1),\varLambda (\varvec{A}_u)) > B'\) simultaneously for all u with overwhelming probability over the randomness of \(\mathsf {TrapGen}\) (using a union bound, as in [14, Lemma 5.3] for instance). Then, by Lemma 2.8, the scheme is correct as long as \(B \le B'\), or equivalently \(\sigma m^{3/2} \cdot \omega (\sqrt{\log n}) \le q\).
Theorem 2.9
Assume \(m \ge \varTheta (n \log q)\). The above scheme is tag-IND-CCA2 assuming the hardness of the LWE\(_{\chi , q}\) problem for \(\chi = D_{\mathbb {Z}, \sigma }\).
The precise definition for tag-IND-CCA2 and the proof of the above theorem are provided in the full version [6].
Remark 2.10
If a constant tag u is hardcoded in \(\mathsf {Encrypt}\) and \(\mathsf {Decrypt}\), then the resulting encryption scheme is just an IND-CPA scheme using trapdoors from [27].
Lemma 2.11
Assume \(m \ge \varTheta (n \log q)\). With \(\varvec{A}_0\) sampled as above, except with probability \(2^{-n}\), it holds that for all \(u \in \mathcal U, \eta _{2^{-n}}(\varLambda ^\perp (\varvec{A}_u)) \le C \sqrt{n}\) for some universal constant C.
Proof
Note that \(\varvec{A}_0\) is (about) uniform under the randomness of \(\mathsf {TrapGen}\), and so is \(\varvec{A}_u\) for a fixed \(u \in \mathcal U\). Apply Lemmas 2.4 and 2.5 with \(\epsilon =8^{-n} / 2\) and \(\delta =4^{-n}\) to \(\varvec{A}_u\), ensuring that \(\eta _{2^{-n}}(\varLambda ^\perp (\varvec{A}_u)) \le C \sqrt{n}\) except with probability \(\delta \). Conclude by the union bound over the \(2^n\) elements \(u \in \mathcal U\). \(\square \)
2.3 Approximate Smooth Projective Hash Functions
We consider approximate smooth projective hash functions (approximate SPHFs) defined in [22].
Languages. We consider a family of languages \({(\mathscr {L}_{{\mathsf {lpar}},\mathsf {ltrap}})}_{{\mathsf {lpar}},\mathsf {ltrap}}\) indexed by some parameter \({\mathsf {lpar}}\) and some trapdoor \(\mathsf {ltrap}\), together with a family of NP languages \({(\widetilde{\mathscr {L}}_{{\mathsf {lpar}}})}_{{\mathsf {lpar}}}\) indexed by some parameter \({\mathsf {lpar}}\), with witness relation \(\widetilde{\mathscr {R}}_{{\mathsf {lpar}}}\), such that:

where \({(\mathcal {X}_{\mathsf {lpar}})}_{\mathsf {lpar}}\) is a family of sets. The trapdoor \(\mathsf {ltrap}\) and the parameter \({\mathsf {lpar}}\) are generated by a polynomial-time algorithm \(\mathsf {Setup.lpar}\) which takes as input a unary representation of the security parameter n. We suppose that membership in \(\mathcal {X}_{\mathsf {lpar}}\) and \(\widetilde{\mathscr {R}}_{{\mathsf {lpar}}}\) can be checked in polynomial time given \({\mathsf {lpar}}\) and that membership in \(\mathscr {L}_{{\mathsf {lpar}},\mathsf {ltrap}}\) can be checked in polynomial time given \({\mathsf {lpar}}\) and \(\mathsf {ltrap}\). The parameters \({\mathsf {lpar}}\) and \(\mathsf {ltrap}\) are often omitted when they are clear from context.
We are mostly interested in languages of ciphertexts.
Example 2.12
(Languages of Ciphertexts). Let \((\mathsf {KeyGen},\mathsf {Encrypt},\mathsf {Decrypt})\) be a labeled encryption scheme. We define the following languages (\(\mathsf {Setup.lpar}= \mathsf {KeyGen}\) and \((\mathsf {ltrap},{\mathsf {lpar}}) = (\mathsf {dk},\mathsf {ek})\)):

where the witness relation \(\widetilde{\mathscr {R}}\) is implicitly defined as: \(\widetilde{\mathscr {R}}( (\mathsf {label}, C, M),\rho ) = 1\) if and only if \(C = \mathsf {Encrypt}(\mathsf {ek}, \mathsf {label}, M; \rho )\).
Approximate SPHFs. Let us now define approximate SPHFs following [22].
Definition 2.13
Let \({(\widetilde{\mathscr {L}}_{{\mathsf {lpar}}} \subseteq \mathscr {L}_{{\mathsf {lpar}},\mathsf {ltrap}} \subseteq \mathcal {X}_{{\mathsf {lpar}}})}_{{\mathsf {lpar}},\mathsf {ltrap}}\) be languages defined as above. An approximate smooth projective hash function (SPHF) for these languages is defined by four probabilistic polynomial-time algorithms:
-
\(\mathsf {HashKG}({\mathsf {lpar}})\) generates a hashing key \(\mathsf {hk}\) for the language parameter \({\mathsf {lpar}}\);
-
 derives a projection key \(\mathsf {hp}\) from the hashing key \(\mathsf {hk}\), the language parameter \({\mathsf {lpar}}\), and the word
derives a projection key \(\mathsf {hp}\) from the hashing key \(\mathsf {hk}\), the language parameter \({\mathsf {lpar}}\), and the word  ;
; -
 outputs a hash value \(\mathsf {H}\in {\{0,1\}}^\nu \) (for some positive integer \(\nu = \varOmega (n)\)) from the hashing key \(\mathsf {hk}\), for the word
outputs a hash value \(\mathsf {H}\in {\{0,1\}}^\nu \) (for some positive integer \(\nu = \varOmega (n)\)) from the hashing key \(\mathsf {hk}\), for the word  and the language parameter \({\mathsf {lpar}}\);
and the language parameter \({\mathsf {lpar}}\); -
 outputs a projected hash value \(\mathsf {pH}\in {\{0,1\}}^\nu \) from the projection key \(\mathsf {hp}\), and the witness
outputs a projected hash value \(\mathsf {pH}\in {\{0,1\}}^\nu \) from the projection key \(\mathsf {hp}\), and the witness  , for the word
, for the word  (i.e.,
(i.e., 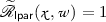 ) and the language parameter \({\mathsf {lpar}}\);
) and the language parameter \({\mathsf {lpar}}\);
which satisfy the following properties:
-
Approximate correctness. For any \(n \in \mathbb {N}\), if
 , with overwhelming probability over the randomness of \(\mathsf {Setup.lpar}\), for any
, with overwhelming probability over the randomness of \(\mathsf {Setup.lpar}\), for any  (and associated witness
(and associated witness  ), the value \(\mathsf {H}\) output by
), the value \(\mathsf {H}\) output by  is approximately determined by
is approximately determined by 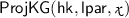 relative to the Hamming metric. More precisely, writing \(\mathsf {HW}(a,b)\) the Hamming distance between two strings \(a,b \in {\{0,1\}}^\nu \), the SPHF is \(\epsilon \)-correct, if:
relative to the Hamming metric. More precisely, writing \(\mathsf {HW}(a,b)\) the Hamming distance between two strings \(a,b \in {\{0,1\}}^\nu \), the SPHF is \(\epsilon \)-correct, if: 
where the probability is taken over the choice of
 and the random coins of \(\mathsf {Hash}\) and \(\mathsf {ProjHash}\).Footnote 7
and the random coins of \(\mathsf {Hash}\) and \(\mathsf {ProjHash}\).Footnote 7
-
Smoothness. For any \(n \in \mathbb {N}\), if
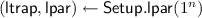 , with overwhelming probability over the randomness of \(\mathsf {Setup.lpar}\), for all
, with overwhelming probability over the randomness of \(\mathsf {Setup.lpar}\), for all 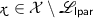 the following distributions have statistical distance negligible in n:
the following distributions have statistical distance negligible in n: 
Finally, an approximate SPHF is called an SPHF if it is 0-correct. In that case, we also say that the SPHF is statistically correct.
Approximate Word-Independent SPHFs. For some applications, in particular the one-round PAKE from [23], a stronger notion of SPHF is required, where the projection key \(\mathsf {hp}\) does not depend on the word  and the smoothness holds even if the word is chosen adaptively after seeing the projection key. We call such SPHFs approximate word-independent SPHFs and we formally define them in the full version [6].
and the smoothness holds even if the word is chosen adaptively after seeing the projection key. We call such SPHFs approximate word-independent SPHFs and we formally define them in the full version [6].
Approximate Universal Bit-PHFs. Instead of directly building (approximate) (word-independent) SPHF, we actually build what we call (approximate) (word-independent) universal bit-PHF.
Definition 2.14
An approximate universal bit projective hash function (bit-PHF) is defined as in Definition 2.13 except that the hash values are bits (\(\nu = 1\)), and that approximate correctness and smoothness are replaced by the following properties:
-
Approximate correctness. The bit-PHF is \(\epsilon \)-correct if for any \(n \in \mathbb {N}\), if
 , with overwhelming probability over the randomness of \(\mathsf {Setup.lpar}\), for any
, with overwhelming probability over the randomness of \(\mathsf {Setup.lpar}\), for any  :
: 
where the probability is taken over the choice of
 and the random coins of \(\mathsf {Hash}\) and \(\mathsf {ProjHash}\).
and the random coins of \(\mathsf {Hash}\) and \(\mathsf {ProjHash}\). -
Universality. Footnote 8 The bit-PHF is \(\epsilon \)-universal if, for any \(n \in \mathbb {N}\), if
 , with overwhelming probability over the randomness of \(\mathsf {Setup.lpar}\), for any word
, with overwhelming probability over the randomness of \(\mathsf {Setup.lpar}\), for any word 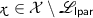 , any projection key \(\mathsf {hp}\):
, any projection key \(\mathsf {hp}\): 
where the probability is taken over the choice of
 and the random coins of \(\mathsf {Hash}\). The bit-PHF is said to be statistically universal if it is \({{\mathrm{negl}}}(n)\)-universal. Otherwise, the bit-PHF is said to be imperfectly universal.
and the random coins of \(\mathsf {Hash}\). The bit-PHF is said to be statistically universal if it is \({{\mathrm{negl}}}(n)\)-universal. Otherwise, the bit-PHF is said to be imperfectly universal.
An approximate bit-PHF is called a bit-PHF if it is \({{\mathrm{negl}}}(n)\)-correct. In that case, the bit-PHF is said to be statistically correct. Furthermore, an (approximate) bit-PHF is called an (approximate) (word-independent) bit-PHF, if \(\mathsf {hp}\) does not depend on the word  .
.
From Bit-PHFs to SPHFs. In the full version [6], we show how to generically convert an approximate \(\epsilon \)-correct \({{\mathrm{negl}}}(n)\)-universal bit-PHF into an approximate \((\epsilon +\epsilon ')\)-correct SPHF (for any positive constant \(\epsilon '\)) and then into an SPHF. This is used in our first construction in Sect. 3. These transformations were implicit in [22]. We should point out that even if the original bit-PHF was word-independent, the resulting (approximate) SPHF would still not be word-independent: its projection key depends on the word  . If there was way to avoid this restriction, we actually would get the first one-round key exchange based on LWE with polynomial modulus.
. If there was way to avoid this restriction, we actually would get the first one-round key exchange based on LWE with polynomial modulus.
In the full version [6], we also show how to generically convert an \(\epsilon \)-universal word-independent bit-PHF into a word-independent SPHF, by amplifying the smoothness or universality property (assuming \(1-\epsilon \ge 1/{{\mathrm{poly}}}(n)\)). We should point out that the original word-independent bit-PHF is supposed to be statistically correct, contrary to the previous transformation where it could just be approximately correct.
We recall that the above transformations were summarized in Fig. 2 together with our results.
3 SPHF for IND-CCA2 Ciphertexts
As we have shown in Sect. 2.3, there exists a generic transformation from approximate bit-PHF to a regular approximate SPHF or even classical SPHF. So, in this section, we are going to focus on building such an approximate bit-PHF. For the sake of simplicity, in this section we often call such an approximate bit-PHF simply a bit-PHF.
3.1 Languages and Natural Bit-PHF
Languages. We want to construct an (approximate) bit-PHF for the language of ciphertexts (Example 2.12) for our IND-CCA2 LWE encryption à la Micciancio-Peikert described in Sect. 2.2. More generally our approach works with typical trapdoored LWE encryption schemes [9, 14].
We first remark that it is sufficient to construct a bit-PHF for the tag-IND-CCA2 version, i.e., for the following languages:

where \(u \in \mathcal U, \varvec{c} \in \mathbb {Z}_q^m, \mu \in {\{0,1\}}\),  , and where \(\mathsf {Encrypt}, \mathsf {Decrypt}, B\), and \(B'\) are defined in Sect. 2.2. Indeed, the signature parts, used to transform the tag-IND-CCA2 encryption scheme into a labeled IND-CCA2 encryption scheme (see the full version [6]), can be publicly checked by anyone, therefore one can generically adapt the bit-PHF by overriding \(\mathsf {Hash}\) to a fresh uniform random value when the signature is invalid.
, and where \(\mathsf {Encrypt}, \mathsf {Decrypt}, B\), and \(B'\) are defined in Sect. 2.2. Indeed, the signature parts, used to transform the tag-IND-CCA2 encryption scheme into a labeled IND-CCA2 encryption scheme (see the full version [6]), can be publicly checked by anyone, therefore one can generically adapt the bit-PHF by overriding \(\mathsf {Hash}\) to a fresh uniform random value when the signature is invalid.
We can now fix the tag \(u \in \mathcal U\) for the rest of this section, and will simply denote \(\varvec{A}\) for \(\varvec{A}_u\) and \(\varLambda \) for \(\varLambda (\varvec{A}_u)\). Also, note that \((u, \varvec{c}, 1) \in \widetilde{\mathscr {L}}\) (resp. \(\mathscr {L}\)) is equivalent to \((u, \varvec{c} - \mathsf {Encode}(1), 0) \in \widetilde{\mathscr {L}}\) (resp \(\mathscr {L}\)). Therefore we can focus only on the languages of ciphertexts of 0 for a fixed tag u, and we restrict our languages to

for the rest of this section.
Natural Bit-PHF. A natural approach to define an approximate bit-PHF is the following:
-
\(\mathsf {HashKG}(\varvec{A})\) outputs
 ;
; -
\(\mathsf {ProjKG}(\varvec{h}, \varvec{A})\) outputs \(\mathsf {hp}= \varvec{p} = \varvec{A}^t \varvec{h}\);
-
\(\mathsf {Hash}(\varvec{h}, \varvec{A}, \varvec{c})\) outputs \(\mathsf {H}= R(\langle \varvec{h}, \varvec{c} \rangle )\);
-
\(\mathsf {ProjHash}(\varvec{p}, \varvec{A}, \varvec{c}, (\varvec{s}, \varvec{e}))\) outputs \(\mathsf {pH}= R(\langle \varvec{p}, \varvec{s} \rangle )\);
where R is a rounding function to be chosen later and \(s > 0\) is a parameter to be chosen later too.
3.2 Universality
Naive Approach. For now let us just assume \(R : \mathbb {Z}_q \rightarrow \mathbb {Z}_2\) to be the usual rounding function \(R(x) = \lfloor 2x/q \rceil \bmod 2\), as in [22]. We have:
which guarantees correctness whenever \(c \in \widetilde{\mathscr {L}}\). Indeed \(\langle \varvec{h}, \varvec{c} \rangle \) is almost uniform for large enough parameter s, therefore \(R(\langle \varvec{h}, \varvec{c} \rangle ) = R(\langle \varvec{p}, \varvec{s} \rangle )\) will hold except with probability \({\approx }2|\langle \varvec{h}, \varvec{e} \rangle |/q\).
For universality, we need to prove that \(\mathsf {Hash}(\varvec{h}, \varvec{A}, \varvec{c}) = \langle \varvec{h}, \varvec{c} \rangle \) is uniform given the knowledge of \(\varvec{A}, \varvec{p}\) and \(\varvec{c}\), when \(\varvec{c} \not \in \mathscr {L}\). Unfortunately, this seems to require a stronger assumption than \(\varvec{c} \not \in \mathscr {L}\), more precisely, that \(j \cdot \varvec{c} \not \in \mathscr {L}\) for all \(j \in \mathbb {Z}_q^*\): this is the key lemma [14, Lemma 5.3] (from [22, Lemma 2]).
The caveat is that it is necessary not only for \(\varvec{c}\) to be far from \(\varLambda \), but also for all its non-zero multiples modulo q: the language is extended to  . Algorithmically, the price to pay is that the decryption function must be changed, and that the usual LWE decryption now must be attempted for each multiple \(j \varvec{c}\) of \(\varvec{c}\) to ensure universality for words outside \(\mathscr {L}'\). This makes the new decryption very inefficient since q is typically quite a large \({{\mathrm{poly}}}(n)\). This change of language is also a technical hassle for constructing protocols above the bit-PHF (or the resulting SPHF).
. Algorithmically, the price to pay is that the decryption function must be changed, and that the usual LWE decryption now must be attempted for each multiple \(j \varvec{c}\) of \(\varvec{c}\) to ensure universality for words outside \(\mathscr {L}'\). This makes the new decryption very inefficient since q is typically quite a large \({{\mathrm{poly}}}(n)\). This change of language is also a technical hassle for constructing protocols above the bit-PHF (or the resulting SPHF).
Note that the key lemma ensures uniformity of \(\langle \varvec{h}, \varvec{c} \rangle \), while we only need the uniformity of \(R(\langle \varvec{h}, \varvec{c} \rangle )\). We show in the technical overview of the introduction that this condition is truly necessary and is not an artifact of the proof, at least for \(j = 3\) by considering \(\varvec{c} = \varvec{A} \varvec{s} + (0, \dots , 0, q/3)^t\) (with q assumed to be divisible by 3 for the sake of simplicity).
But what should happen in more general cases?
Harmonic Analysis. Let us fix \(\varvec{p} \in \mathbb {Z}_q^n\) and \(\varvec{c} \in \mathbb {Z}_q^m\). For the rest of the section, we restrict the rounding function R to have binary values \(\{0,1\}\), yet this function may be probabilistic.
We want to study the conditional probability  , where the probability is taken over the randomness of R and the distribution of \(\varvec{h}\) (conditioned on \( \varvec{h}^t \varvec{A} = \varvec{p}^t\)); we want P to be not too far from 1/2 when \(\varvec{c} \not \in \mathscr {L}\). For \(x \in \mathbb {Z}\), denote by r(x) the probability that \(R(x \bmod q) = 1\). Because \(r: \mathbb {Z}\rightarrow [0,1]\) is q-periodic, it can be interpolated over the reals by a function of the form:
, where the probability is taken over the randomness of R and the distribution of \(\varvec{h}\) (conditioned on \( \varvec{h}^t \varvec{A} = \varvec{p}^t\)); we want P to be not too far from 1/2 when \(\varvec{c} \not \in \mathscr {L}\). For \(x \in \mathbb {Z}\), denote by r(x) the probability that \(R(x \bmod q) = 1\). Because \(r: \mathbb {Z}\rightarrow [0,1]\) is q-periodic, it can be interpolated over the reals by a function of the form:
where the complex values \(\hat{r}_j \in \mathbb C\) are the Fourier coefficients of \(r :\mathbb Z \rightarrow [0,1]\). Note that as we are only interested in the restriction of r on \(\mathbb {Z}\) (which is q-periodic), we only need q harmonics to fully describe r. Also note that \(r(x) \in [0,1]\) for all \(x \in \mathbb {Z}_q\), so that \(|\hat{r}_j| \le 1\) for all j.
We rewrite:
where \(\varvec{h}_0\) is any vector of the coset \(\varLambda ^\bot _{\varvec{p}}\). We will now apply the Poisson Summation Formula (Lemma 2.6): \(f(\varLambda ^\bot ) = \det ({(\varLambda ^\bot )}^*) \hat{f}({(\varLambda ^\bot )}^*) = \det (\frac{1}{q}\varLambda ) \hat{f}(\frac{1}{q} \varLambda )\). Set \(f(\varvec{h}) = (\rho _s \cdot e_{j \varvec{c} / q})(\varvec{h} + \varvec{h}_0)\). We have:
We proceed:
Assuming \(s \ge \eta _\epsilon (\varLambda ^\bot )\) for some negligible \(\epsilon \) ensures that \(\frac{\det ({(\varLambda ^\bot )}^*) s^m}{\rho _s(\varLambda ^\bot _{\varvec{p}})} = 1 + O(\epsilon )\) by Lemma 2.3. We shall split the sum into three parts:
-
\(j = 0, \varvec{y} = \varvec{0}\), contributing exactly \(\hat{r}_0\) (where \(\hat{r}_0 = \frac{1}{q}\sum _{x\in \mathbb {Z}_q} r(x) \in [0,1]\)),
-
\(j = 0, \varvec{y} \ne \varvec{0}\), contributing at most \(|\hat{r}_0| \rho _{q/s}(\varLambda \setminus \{\varvec{0}\})\) in absolute value,
-
\(j \ne 0\), contributing at most \(|\hat{r}_j| \rho _{q/s}(\varLambda - j\varvec{c})\) in absolute value for each j.
We can now bound P:
We now want to bound the right-hand side using Lemma 2.1, with \(c=1\) for simplicity. Fix \(j \in \mathbb {Z}_q \setminus \{0 \}\), and let \(\alpha = q \sqrt{m}/s\). If \(\alpha < d(j\varvec{c}, \varLambda )\), then \((\varLambda -j\varvec{c}) \setminus \alpha \mathcal B = (\varLambda - j\varvec{c})\). Also, note that \(\rho _{q/s}(\varLambda ) = \rho _{1/s}(\frac{1}{q}\varLambda ) = \rho _{1/s}({(\varLambda ^\bot )}^*)\). So, as long as \(s\ge \eta _\epsilon (\varLambda ^\bot )\) for some negligible \(\epsilon \) (which we already assumed earlier), it holds that \(\rho _{q/s}(\varLambda ) \le 1+ \epsilon \) by definition of \(\eta _{\epsilon }(\varLambda ^\bot )\). Under those conditions, \(\rho _{q/s}(\varLambda - j\varvec{c}) = \rho _{q/s}((\varLambda -j \varvec{c}) \setminus \alpha \mathcal {B}) \le 2C^m \rho _{q/s}(\varLambda ) \le 2C^m (1+\epsilon )\) is negligible. Using Lemma 2.1, we deduce the following:
Theorem 3.1
Fix \(\varvec{A} \in \mathbb {Z}_q^{m\times n}, \varvec{c} \in \mathbb {Z}^m_{q}\), and \(\varvec{p} \in \mathbb {Z}^n_{q}\), where m is polynomial in n. Fix a probabilistic rounding function \(R:\mathbb {Z}_q \rightarrow \{0,1\}\) such that for all \(x\in \mathbb {Z}_q\),
where \(J \subseteq \mathbb {Z}_q\) and \(\hat{r}_j \in \mathbb {C}\). Let \(s \ge \eta _\epsilon (\varLambda ^\bot (\varvec{A}))\) for some \(\epsilon = {{\mathrm{negl}}}(n)\). Assume furthermore that
Denote  , where the probability is taken over the randomness of R, and the distribution of
, where the probability is taken over the randomness of R, and the distribution of  , conditioned on \(\varvec{h}^t \varvec{A} = \varvec{p}^t\). Then:
, conditioned on \(\varvec{h}^t \varvec{A} = \varvec{p}^t\). Then:
Setting up the Rounding Function. If one wishes to avoid having to attempt decryption of many multiples of the ciphertext \(\varvec{c}\), one should choose a probabilistic rounding function with a small number of harmonics.
In particular, the typical deterministic rounding function \(R(x) = \lfloor 2x/q \rceil \bmod 2\)—the so-called square-signal—and has harmonic coefficients \(\hat{r}_j\) decreasing as \(\varTheta (1/j)\) in absolute value (for odd \(j \in \{\lceil -q/2 \rceil ,\dots ,\lfloor q/2 \rfloor \}\)). With such a rounding function, one would still need to attempt trapdoor inversion for q/2 many multiples of \(\varvec{c}\), as it was already the case in [22].
On the contrary, one may easily avoid costly harmonics by setting the rounding function so that \(2 r(x) = 1 + \cos (2 \pi x/q)\), which has Fourier coefficients \(\hat{r}_0 = 1/2, \hat{r}_1 = \hat{r}_{-1} = 1/4\), and \(\hat{r}_j = 0\) for any other j.Footnote 9 More precisely, we have the following corollary by remarking that when \(\varvec{c} \notin \mathscr {L}\) and \(\alpha = q \sqrt{m}/s < B'\), we have \(d(\varvec{c}, \varLambda ) \ge B'\) and \((\varLambda - \varvec{c}) \setminus (\alpha \mathcal {B}) = (\varLambda - \varvec{c})\).
Corollary 3.2
Let \(\varvec{A} \in \mathbb {Z}_q^{m\times n}\) with \(m = \varTheta (n \log q)\), and fix \(\varvec{p} \in \mathbb {Z}_q^n\). Let \(B' = q/\varTheta ( \sqrt{m})\), and  . Suppose that R satisfies:
. Suppose that R satisfies:
and let \(s \ge \eta _\epsilon (\varLambda ^\bot (\varvec{A}))\) for some \(\epsilon = {{\mathrm{negl}}}(n)\). Suppose also that: \(s > \frac{q \sqrt{m}}{B'}\).
Denote again  , where the probability is taken over the randomness of R, and the distribution of
, where the probability is taken over the randomness of R, and the distribution of  , conditioned on \(\varvec{h}^t \varvec{A} = \varvec{p}^t\). Then, for all \(\varvec{c} \not \in \mathscr {L}\):
, conditioned on \(\varvec{h}^t \varvec{A} = \varvec{p}^t\). Then, for all \(\varvec{c} \not \in \mathscr {L}\):
where \(C = \sqrt{2\pi e} \cdot e^{-\pi } < 1\).
3.3 Approximate Correctness
Let us check that the scheme above achieves approximate correctness, that is, for all \(\varvec{c} \in \widetilde{\mathscr {L}}, \mathsf {Hash}(\varvec{h}, \varvec{A}, \varvec{c}) = \mathsf {ProjHash}(\varvec{p}, \varvec{A}, \varvec{c}, (\varvec{s}, \varvec{e}))\) with probability substantially greater than 1/2. Using our rounding function R, this means that we want \(R(\langle \varvec{h}, \varvec{c} \rangle )\) and \(R(\langle \varvec{p}, \varvec{s} \rangle )\) to output the same bit with some probability Q substantially greater than 1/2, where the two applications of R use independent coins.
Recall that r(x) is the probability that the rounding function R outputs 1 on input x, and that for \(\varvec{c} \in \widetilde{\mathscr {L}}\), we can write \(\langle \varvec{h}, \varvec{c} \rangle = \langle \varvec{p}, \varvec{s} \rangle + \langle \varvec{h}, \varvec{e} \rangle \), where \(\varvec{c} = \varvec{A} \varvec{s} + \varvec{e}\). We argue that as long as \(\langle \varvec{h}, \varvec{e} \rangle \) is small with respect to q, then our scheme achieves approximate correctness:
Lemma 3.3
Fix \(\varvec{A} \in \mathbb {Z}_q^{m\times n}\) and \(\varvec{c} = \varvec{A} \varvec{s} + \varvec{e} \in \widetilde{\mathscr {L}}\), where m and q are polynomial in n, and where \(\Vert \varvec{e}\Vert \le B = 2 t \sqrt{m}\). Let \(s\ge \eta _\epsilon (\varLambda ^\bot (\varvec{A}))\) for some \(\epsilon = {{\mathrm{negl}}}(n)\). Assume that R is the cosine rounding function (Eq. (1)). Let Q be the probability that \( R(\langle \varvec{A}^t \varvec{h}, \varvec{s} \rangle ; \mathsf {coins}_1)\) and \(R(\langle \varvec{h}, \varvec{c} \rangle ;\mathsf {coins}_2)\) output the same bit, over the randomness of  , and the randomness of the two independent coins \(\mathsf {coins}_1\) and \(\mathsf {coins}_2\) used by R. If \( t s m = o(q)\), then \(Q = 3/4 + o(1)\).
, and the randomness of the two independent coins \(\mathsf {coins}_1\) and \(\mathsf {coins}_2\) used by R. If \( t s m = o(q)\), then \(Q = 3/4 + o(1)\).
Proof
As \(s\ge \eta _\epsilon (\varLambda ^\bot )\) for \(\epsilon = {{\mathrm{negl}}}(n)\), the distribution of \(\varvec{h}^t \varvec{A} \), when  , is at negligible statistical distance from uniform.
, is at negligible statistical distance from uniform.
Therefore, Q is negligibly close to \( \Pr [R(x;\mathsf {coins}_1) = R(x + \langle \varvec{h}, \varvec{e} \rangle ; \mathsf {coins}_2)] \) where the probability is taken over uniform \(x \in \mathbb {Z}_q\),  , and the randomness of the two independent coins \(\mathsf {coins}_1\) and \(\mathsf {coins}_2\) used by R.
, and the randomness of the two independent coins \(\mathsf {coins}_1\) and \(\mathsf {coins}_2\) used by R.
Then:
As \(t s m = o(q)\), we have \(\langle \varvec{h}, \varvec{e} \rangle = o(q)\) with overwhelming probability. As \(\cos \) is a Lipschitz continuous function, we can approximate the sum by an integral: \(Q = \frac{1}{2} + \frac{1}{2}\int _{0}^{1} \cos ^{2}(2\pi x) dx + o(1)= \frac{3}{4} + o(1)\). \(\square \)
3.4 Wrap-Up
Consider the bit-PHF described in Sect. 3.1 instantiating R with the cosine rounding function (Eq. (1)), together with the encryption scheme of Sect. 2.2. Let us now show that all the parameters can be instantiated to satisfy security and correctness of the encryption scheme, simultaneously with statistical universality and approximate correctness of the bit-PHF.
IND-CCA2. To base the security of the scheme described in Sect. 2.2 on LWE\(_{\chi , q}\) for \(\chi = D_{\mathbb {Z},\sigma }\) and \(\sigma = 2\sqrt{n}\),Footnote 10 we apply Theorem 2.9 with \(m = \varTheta (n \log q)\) and \(t = \sqrt{mn} \cdot \omega (\sqrt{\log n})\).
Decryption Correctness. For the encryption scheme to be correct, we want \(B < B'\), recalling that  and
and  .
.
Universality. In Corollary 3.2, we used the hypothesis \(s \ge \eta _{\epsilon }(\varLambda ^\bot (\varvec{A}_u))\) for some negligible \(\epsilon \). Assuming \(s \ge \varTheta (\sqrt{n})\), one can apply Lemma 2.11, to ensure the above hypothesis for \(\epsilon = 2^{-n}\) simultaneously for all \(u \in \mathcal U\) except with probability \(2^{-n}\) over the randomness of \(\mathsf {TrapGen}\).
Still in Corollary 3.2, we also needed \(s > q \sqrt{m} / B'\), where \( B' = {q}/{\varTheta (\sqrt{m})} \). This holds for \(s = \varTheta (m) \).
Approximate correctness. For Lemma 3.3, we assumed that \(t s m = o(q)\). Equivalently, it is sufficient that \(s m^{3/2} n^{1/2} \omega (\sqrt{\log n}) = o(q)\).
Summary. Therefore, all the desired conditions can be satisfied with \(q = \tilde{\varTheta }(n^3)\), \(m = \tilde{\varTheta }(n)\), \(s = \tilde{\varTheta }(n)\), and \(t = \tilde{\varTheta }(n)\). We have proved the following:
Theorem 3.4
Set parameters \(q = \tilde{\varTheta }(n^3), m = \tilde{\varTheta }(n), s = \tilde{\varTheta }(n), t = \tilde{\varTheta }(n)\). Define a probabilistic rounding function \(R:\mathbb {Z}_q \rightarrow \{0,1 \}\) such that \(\Pr [R(x)=1] = 1/2 + \cos \left( 2\pi x/ q \right) / 2 \). Then, (i) the encryption scheme of Sect. 2.2 is correct and tag-IND-CCA2 under the hardness of LWE\(_{\chi , q}\) for \(\chi = D_{\mathbb {Z}, 2\sqrt{n}}\); and (ii) the bit-PHF described in Sect. 3.1 achieves statistical universality and \((1/4-o(1))\)-correctness.
4 Word-Independent SPHF for IND-CPA Ciphertexts
4.1 Overview
In the previous section, we built a bit-PHF with \({{\mathrm{negl}}}(n)\)-universality but approximate correctness. Even though correctness can be amplified, the transformation inherently makes the new projection key depend on the word we want to hash, even if that was not the case for the initial bit-PHF.
We now build a bit-PHF with statistical correctness and K-universality for some universal constant \(K<1\) (but using a super-polynomial LWE modulus q). The main benefit of such a construction is that amplifying universality can be done regardless of the word we want to hash, that is, the projection key will not depend on the word. When the tag u of the ciphertext \(\varvec{c}\) is known in advance or is constant (in which case, the encryption scheme is only IND-CPA instead of IND-CCA2), we therefore get a word-independent bit-PHF which can be transformed into a word-independent SPHF. This is the first word-independent SPHF for any lattice-based language.
We use the same natural approach as described in Sect. 3.1. The only differences with the construction in the previous section are the probabilistic rounding function we use, and the parameters necessary to argue correctness and universality. Recall that in the last section, we used a rounding function with only low order harmonics to get \({{\mathrm{negl}}}(n)\)-universality.
The starting point is the observation that, for the naive square rounding introduced in the previous section, the correctness is statistical, but clearly not \({{\mathrm{negl}}}(n)\)-universal, depending on which word \(\varvec{c}\) is hashed (as seen in the two case studies in the technical overview in the introduction, where \(j\cdot \varvec{c}\) is close to \(\varLambda \) for some \(j\in \mathbb {Z}_q^*\)). However, the distribution of \(R(\langle \varvec{h}, \varvec{c}\rangle )\) conditioned on \(\varvec{h}^t \varvec{A}\) might still have enough entropy to give us K-universality, for some constant \(K<1\). In other words, we can hope that  for all \(\varvec{c} \in \mathbb {Z}_q^{m}\).
for all \(\varvec{c} \in \mathbb {Z}_q^{m}\).
Let \(R^\sharp \) be a rounding function defined by: \(R^\sharp (x) = 1 + \lfloor 2x/q \rceil \bmod 2\), that is:
Using this rounding function gives good correctness: when \(s\ge \eta _\epsilon (\varLambda ^{\bot }), \langle \varvec{h}, \varvec{c} \rangle \) is statistically close to uniform in \([-q/2, q/2]\), and therefore \(R^\sharp (\langle \varvec{h}, \varvec{c} \rangle )\) is a uniform bit up to some statistical distance \(O(\epsilon + 1/q)\) (due to the fact that q is odd). So for super-polynomial q, we get statistical correctness using \(R^\sharp \) as rounding function, as long as \(\langle \varvec{h}, \varvec{e}\rangle \) is sufficiently small with respect to q.
For universality, we express the probability distribution defined by \(R^\sharp \), seen as a q-periodic function over \(\mathbb R\), as a Fourier series:

where \(\hat{r}^\sharp _j\) are the Fourier coefficients of the q-periodic function \(r^\sharp :\mathbb {R} \rightarrow \mathbb {R}\).
However, one can show that \(|\hat{r}^\sharp _j| = \varTheta (1/j)\) (for odd integers j). Therefore, it is not clear how to show universality with a similar analysis as in Sect. 3.2: the total contribution of harmonics j such that \(j\cdot \varvec{c}\) is close to \(\varLambda \) could potentially be arbitrarily large!
To solve this issue, we consider a new rounding function R, which has the same probability distribution as \(R^\sharp \) but on a negligible fraction of integer points (so that statistical correctness is preserved), and such that its Fourier coefficients of high enough order have small enough amplitude.
Then, we use the observation that the set of integers j such that \(j\cdot \varvec{c}\) is in \(\varLambda \) is an ideal of \(\mathbb {Z}\), which is proper if \(\varvec{c}\) itself is not in \(\varLambda \). More generally, the set of small integers \(j \in \mathbb {Z}\) such that \(j\cdot \varvec{c}\) is close to \(\varLambda \) is contained in an ideal of \(\mathbb {Z}\); furthermore, if \(\varvec{c}\) is far from \(\varLambda \), then the smallest such ideal is a proper ideal of \(\mathbb {Z}\). This will allow us to discard all harmonics whose order is not in this ideal. As we will show, the remaining harmonics necessarily have destructive interferences, which allows us to establish K-universality for some constant \(K<1\).
The roadmap follows. First, in Sect. 4.2, we smooth the discontinuities of the probability distribution of the square rounding function \(r^\sharp \) so that the Fourier coefficients of high order have small magnitude, but such that we keep statistical correctness. Then to prove universality, in Sect. 4.3, we show that for \(\varvec{c}\) far from \(\varLambda \), the set of small \(j \in \mathbb {Z}\) such that \(j\cdot \varvec{c}\) is close to \(\varLambda \) is contained in a proper ideal of \(\mathbb {Z}\). Finally, in Sect. 4.4 we show that the distribution of \(R(\langle \varvec{h}, \varvec{c}\rangle )\) conditioned on \(\varvec{h}^t \varvec{A}\) has some bounded min entropy.
4.2 Smoothing the Discontinuities: A New Rounding Function
In the following, unless specified otherwise, we will see \(\mathbb {Z}_q\) as embedded in \(\{\lceil -q/2 \rceil ,\dots , \lfloor q/2 \rfloor \}\), and the canonical period we use for q-periodic functions will be \([-q/2, q/2]\). Recall that \(r^\sharp \) satisfies:

In particular, \(r^\sharp \) has two discontinuities on q/4 and on \(-q/4\). To smooth those discontinuities, we consider the convolution product of the square signal \(r^\sharp \) with a rectangular signal of appropriate width T such that \(T/q = {{\mathrm{negl}}}(n)\). More precisely, consider the q-periodic function \(r^\flat \) defined on \([-q/2, q/2]\) by:
We define a new rounding function R such that for all  (see Fig. 1):
(see Fig. 1):

where, in this context, \(\odot \) corresponds to the convolution of q-periodic functions.
Intuitively, this corresponds to replace the discontinuities on \(r^\sharp (\pm q/4)\) by a linear slope ranging from \(\pm q/4 - T\) to \(\pm q/4 + T\) (see Fig. 1). Therefore, over \([-q/2,q/2]\), the functions r and \(r^\sharp \) only differ on at most \(4\lceil T \rceil \) integer points (the points on the slope). Recall that if \(s\ge \eta _\epsilon (\varLambda ^\bot )\) for some negligible \(\epsilon \), then \(\langle \varvec{h}, \varvec{c} \rangle \) is statistically close to uniform in \(\{\lceil -q/2 \rceil ,\dots , \lfloor q/2 \rfloor \}\). Therefore, if \(\langle \varvec{h}, \varvec{e} \rangle /q\) and T/q are negligible, then:
and we get statistical correctness using such a rounding function.
Lemma 4.1
(Correctness). Suppose that \(s\ge \eta _\epsilon (\varLambda ^\bot )\) for some \(\epsilon = {{\mathrm{negl}}}(n), t s m/q = {{\mathrm{negl}}}(n)\), and \(T/q = {{\mathrm{negl}}}(n)\). Assume that R satisfies: \(\Pr [R(x)=1] = r(x) = (r^\sharp \odot r^\flat )(x)\). Then the approximate bit-PHF defined in Sect. 3.1 achieves statistical correctness.
Furthermore, r is q-periodic, and can therefore be expressed as a Fourier series:
with Fourier coefficients \(\hat{r}_j\). As \(r = r^\sharp \odot r^\flat \), we have \(\hat{r}_j = q \cdot \hat{r}^\sharp _j \cdot \hat{r}^\flat _j\) for \(j \in \mathbb {Z}\), where \(\hat{r}^\sharp _j\) and \(\hat{r}^\flat _j\) are the Fourier coefficients of the q-periodic functions \(r^\sharp \) and \(r^\flat \) respectively. Thus, \(\hat{r}_0 = 1/2\), and for \(j \in \mathbb {Z}\setminus \{0\}\), the jth harmonic of r is:
4.3 Inclusion of Contributing Harmonics in a Proper Ideal
In the following, we focus on showing that even though we do not have \({{\mathrm{negl}}}(n)\)-universality using this new rounding function, we still have some K-universality for some constant \(K < 1\) (that we can amplify).
We start by a simple useful lemma:
Lemma 4.2
Let \(N=kq/ T\) for some k. Then \(\sum _{\begin{array}{c} j\in \mathbb {Z},\;|j|>N \end{array}} |\hat{r}_j| \le 1/k\).
Proof
It follows from Eq. (2) and the fact that for all \(N>2\): \(\sum _{k=N}^{+\infty } \frac{1}{k^2} \le \sum _{k=N}^{+\infty } \left( \frac{1}{k-1} - \frac{1}{k}\right) = \frac{1}{N-1}\). \(\square \)
Suppose now that \(d(\varvec{c}, \varLambda ) \ge B'\). Consider the set of \(j \in \mathbb {Z}\) such that \(d(j\cdot \varvec{c}, \varLambda ) \le \delta \) for some appropriately chosen \(\delta \). Let  , for our new rounding function R. For any \(\varvec{h_0} \in \varLambda ^{\bot }_{\varvec{p}}\), we can show similarly to Sect. 3.2, that:
, for our new rounding function R. For any \(\varvec{h_0} \in \varLambda ^{\bot }_{\varvec{p}}\), we can show similarly to Sect. 3.2, that:
where \(\frac{\det ({(\varLambda ^\bot )}^*) s^m}{\rho _s(\varLambda ^\bot _{\varvec{p}})} = (1+O(\epsilon ))\) as long as \(s\ge \eta _\epsilon (\varLambda ^\bot )\). Note that \(\sum _{|j|\ge N} |\hat{r}_j|\) can be made arbitrarily small for appropriate N, by Lemma 4.2. Thus only the terms of the sum corresponding to \(|j|\le N\) will have a substantial contribution to the sum above (recall that \(\rho _{q/s}(\varLambda - j\varvec{c}) \le 1+\epsilon \) for all \(\varvec{c}\), for appropriate parameters). Therefore we only consider those small j such that \(|j|<N\) for some appropriately chosen N (with respect to q). Furthermore, for large enough \(\delta \), the terms corresponding to indices j such that \(d(j\cdot \varvec{c},\varLambda ) > \delta \) also have a negligible contribution to the sum by Lemma 2.1. For appropriate parameters N and \(\delta \) to be instantiated later, let:

As a subset of \(\mathbb {Z}, J\) is contained in the ideal \(j_0 \mathbb {Z}\) of \(\mathbb {Z}\), where \(j_0 = \gcd (J)\). Let us show that it is a proper ideal of \(\mathbb {Z}\), i.e., \(j_0 \ne 1\). To do so, we rely on the existence of small Bézout coefficients.
Lemma 4.3
(Corollary of [26, Theorem 9]). Let \(a_1,\dots , a_k \in \mathbb {Z}\), and let \(g=\gcd (a_1,\dots , a_k)\). Then there exists \(u_1,\dots ,u_k \in \mathbb {Z}\) such that the following conditions hold:

We can now prove that J is a proper ideal of \(\mathbb {Z}\):
Lemma 4.4
Suppose that \(\delta N^2 < B'\). Then, for \(\varvec{c} \in \mathbb {Z}_q^m\) such that \(d(\varvec{c}, \varLambda ) > B'\), the set  is contained in a proper ideal of \(\mathbb {Z}\).
is contained in a proper ideal of \(\mathbb {Z}\).
Proof
Let \(j_0 = \gcd (J)\). By definition, \(J\subseteq j_0 \mathbb {Z}\). Suppose by contradiction that \(j_0=1\). By Lemma 4.3, there exists a set of integers \(\{u_j,j\in J\}\) such that \(\sum _{j\in J} u_j\cdot j = 1\) and then \(\sum _{j \in J} u_j \cdot (j \cdot \varvec{c}) = \varvec{c}\). But by definition of \(J, d(j\cdot \varvec{c}, \varLambda ) \le \delta \) for all \(j\in J\), and therefore:
which is absurd as we assumed \(d(\varvec{c}, \varLambda ) > B'\). \(\square \)
4.4 Imperfect Universality from Destructive Interferences
We now want to quantify how biased \(R(\langle \varvec{h}, \varvec{c}\rangle )\) conditioned on \(\varvec{h}^t \varvec{A}\) can be when \(\varvec{c}\) is far from \(\varLambda \). We start from Eq. (3):
where \(\frac{\det ({(\varLambda ^\bot )}^*) s^m}{\rho _s(\varLambda ^\bot _{\varvec{p}})} = 1+O(\epsilon )\) as long as \(s\ge \eta _\epsilon (\varLambda ^\bot )\).
We split the sum into three parts \(P = P_1+P_2+P_3\):
- \(P_1\).:
-
\(|j| > N \wedge j \not \in j_0\mathbb {Z}\): those indices have a negligible contribution to the sum by Lemma 4.2.
- \(P_2\).:
-
\(|j| \le N \wedge j \not \in j_0\mathbb {Z}\): those indices contribute negligibly since \(\rho _{q/s}(\varLambda - j\varvec{c})\) is small as \(j\varvec{c}\) is far from \(\varLambda \) (by definition of \(\delta \) and \(J \subset j_0\mathbb {Z}\)).
- \(P_3\).:
-
\(j \in j_0\mathbb {Z}\): the contributing terms. Unlike the previous ones we won’t use absolute bounds for each term, and must consider destructive interferences.
It remains to study \(P_3\), for which a similar computation as in Sect. 3.2 gives:
If we were to have \(j_0=1\) (i.e. \(j_0\mathbb {Z}= \mathbb {Z}\)), we could compute the inner sum simply by inverse Fourier transform, evaluating r at \(x=\langle \varvec{h}, \varvec{c} \rangle \). Instead, we note that selecting only the harmonics in \(j_0\mathbb {Z}\), corresponds in the temporal domain to averaging the function r over all its temporal shifts by multiples of \(q/j_0\). More formally, recall the identity:
We may now rewrite:
Note that \(\frac{1}{j_0} \sum _{k=0}^{j_0 -1} r^\sharp (x + k\frac{q}{j_0})\) is not too far away from 1/2: if \(j_0\) is even, this is exactly 1/2 (for all x), and if \(j_0=2k+1\), this is either \(k/j_0\) or \((k+1)/j_0\) (depending on x), which is at distance \(1/(2 j_0) \le 1/6\) from 1/2 (recall that \(j_0 > 1\) by Lemma 4.4). Furthermore, we have:
which gives, for all \(x \in [-q/2,q/2]\):
Therefore, \(P_3\) is also not too far from 1/2 as a convex combination of values not too far from 1/2. More precisely we have \(| P_3 - 1/2 | \le 1/6\).
Putting everything together, we can quantify the distance from P to 1/2:
Theorem 4.5
(Universality). Let \(\varvec{A} \in \mathbb {Z}_q^{m\times n}\) with \(m = \varTheta (n \log q)\), and fix \(\varvec{p} \in \mathbb {Z}_q^n\). Let \(B' = q/\varTheta ( \sqrt{m})\), and  . Let R be as defined in Sect. 4.2 and let \(s \ge \eta _\epsilon (\varLambda ^\bot (\varvec{A}))\) for some \(\epsilon = {{\mathrm{negl}}}(n)\). Suppose also that parameters \(T, N, \delta \), and k satisfy \(\delta > \frac{q \sqrt{m}}{s}, N= \frac{kq}{T}\), and \(\delta N^2 < B'\).
. Let R be as defined in Sect. 4.2 and let \(s \ge \eta _\epsilon (\varLambda ^\bot (\varvec{A}))\) for some \(\epsilon = {{\mathrm{negl}}}(n)\). Suppose also that parameters \(T, N, \delta \), and k satisfy \(\delta > \frac{q \sqrt{m}}{s}, N= \frac{kq}{T}\), and \(\delta N^2 < B'\).
Denote again  , where the probability is taken over the randomness of R, and the distribution of
, where the probability is taken over the randomness of R, and the distribution of  , conditioned on \(\varvec{h}^t \varvec{A} = \varvec{p}^t\). Then, for all \(\varvec{c} \not \in \mathscr {L}\):
, conditioned on \(\varvec{h}^t \varvec{A} = \varvec{p}^t\). Then, for all \(\varvec{c} \not \in \mathscr {L}\):
where \(C = \sqrt{2\pi e} \cdot e^{-\pi } < 1\).
Remark 4.6
Informally, this theorem states that the second case study of the technical overview of the introduction is essentially the worst case.
Proof
Writing \(P = P_1 + P_2 + P_3\) as above, we showed that \(|P_3-1/2| \le 1/6\). Moreover, as \(s \ge \eta _\epsilon (\varLambda ^\bot (\varvec{A}))\), we have:
and, for any \(j \in \mathbb {Z}\) and \(\varvec{c}\), we also have:
Therefore, by Lemma 4.2, and as \(\epsilon = {{\mathrm{negl}}}(n)\), we have:
Furthermore, as \(\delta > \frac{q \sqrt{m}}{s}\), and \(|\hat{r}_j| \le 1\) for all j, Lemma 2.1 gives us that \(|P_2| \le 4 N C^m (1+O(\epsilon ))\), which concludes the proof. \(\square \)
4.5 Wrap-Up
Let us now show that all the parameters can be instantiated to get approximate smoothness and correctness for the SPHF, using a rounding function R defined by \(\Pr [R(x)=1] = r^\sharp \odot r^\flat (x)\).
IND-CPA. To apply Theorem 2.9 with Remark 2.10, we can use the fact that \(m = \varTheta (n \log q)\) and \(t = \sqrt{mn} \cdot \omega (\sqrt{\log n})\).
Decryption Correctness. For the encryption scheme to be correct, we want \(B<B'\), with \(B= 2t \sqrt{m}\) and \(B'=q/\varTheta (\sqrt{m})\).
Correctness. For correctness of the bit-PHF, we need a super-polynomial modulus q, and require T/q to be negligible. Furthermore, we need tsm/q to be negligible, so that \(\langle \varvec{h}, \varvec{e} \rangle \) can only take a negligible fraction of values in \(\mathbb {Z}_q\). Also, we need \(s \ge \eta _\epsilon (\varLambda ^\bot (\varvec{A}_u))\), which is satisfied with high probability by Lemma 2.11 for \(\epsilon = 2^{-n}\) as long as \(s \ge \varTheta (\sqrt{n})\).
Bounding the amplitude of high frequencies. The parameter N which upper bounds the elements of J must be taken so that \(\sum _{|j|\ge N} |\hat{r}_j|\) is small. By Lemma 4.2, by taking \(N = k q/T\), this sum is \(\le 1/k\).
Threshold distance to \(\varLambda \) defining J . The parameter \(\delta \), which denotes how close \(j\cdot \varvec{c}\) is close to \(\varLambda \) for \(j \in J\) (Eq. (4)) has to be chosen so that \(N \cdot \rho _{q/s}(\varLambda - \varvec{v})\) must be small whenever \(d(\varvec{v}, \varLambda ) \ge \delta \). As in the analysis for the cosine rounding function, setting \(\delta = q \sqrt{m}/s\) implies that \(\rho _{q/s}(\varLambda - \varvec{v}) \le 2C^m (1+O(\epsilon ))\) by Lemma 2.1.
Showing that \(j_0\ne 1\) . We also required \(\delta N^2 < B'\) to conclude that J was included in a proper ideal of \(\mathbb {Z}\). As we have \(\delta N^2 = \varTheta \left( \frac{q^3 k \sqrt{m}}{s T^2}\right) \), this holds as long as \(s \ge \varOmega (\frac{m k^2 q^2}{T^2}\)).
Putting everything together, we get the following theorem:
Theorem 4.7
Suppose \(q=O(2^n)\) is superpolynomial in \(n, m=\varTheta (n\log q)\). Set parameters: (i) T such that T/q and \(q/T^2\) are both negligible in n (using \(T = q^{2/3}\) for instance), (ii) \(k = \varTheta (n)\), and (iii) \(s\ge \varTheta (\sqrt{n})\) such that \(s/q = {{\mathrm{negl}}}(n)\) and \(s = \varOmega (\frac{m k^2 q^2}{T^2})\), which exists by construction of T. Define a probabilistic rounding function \(R:\mathbb {Z}_q \rightarrow \{0,1 \}\) such that \(\Pr [R(x)=1] = r^\sharp \odot r^\flat (x)\). Then the bit-PHF described in Sect. 3.1 achieves \((1/3 + o(1))\)-universality and statistical correctness.
Proof
The theorem follows from the discussion above and Theorem 4.5 using: (i) \(N = kq/T\) (in which case \(N C^m\) is negligible in n), and (ii) \(\delta = \frac{q\sqrt{m}}{s}\). \(\square \)
5 Applications
In this section, we present several applications of our new construction. It underlines the importance of revisiting this primitive.
5.1 Password-Authenticated Key Exchange
3-Round PAKE. Gennaro and Lindell proposed in [13] a generic framework for building 3-round PAKE protocols based on an IND-CCA2 encryption scheme and an associated SPHF. Later in [22], Katz and Vaikuntanathan refined it to be compatible with approximate SPHF over a CCA2-secure encryption scheme.
We can instantiate the construction in [22] using the encryption scheme à la Micciancio-Peikert in Sect. 2.2 together with an approximate SPHF generically derived from the approximate bit-PHF constructed in Sect. 3. This allows us to achieve a PAKE protocol in three flows, with a polynomial modulus.
Moving to a 2-Round PAKE. An interesting optimization in cryptography is to reduce the number of rounds, so that each user only has to speak once. Is it possible to achieve a PAKE, where each user sends simply one flow?
In [1], the authors revisited the Groce-Katz framework [17]. Their construction (called GK-PAKE) uses a pseudo-random generator, an IND-CPA encryption scheme, with a simple regular SPHF on one hand, and an IND-PCA (Indistinguishable against Plaintext-Checkable Attacks) encryption on the other.
Every IND-CCA2 encryption being also IND-PCA, we can trivially meet the requirements and achieve the expected 2-rounds efficiency, using our SPHF from Sect. 3.Footnote 11 Contrary to the construction of Zhang and Yu [30], we do not need a simulation-sound non-interactive proof (SS-NIZK), which we do not know how to construct from lattice assumptions in the standard model.
Achieving a 1-Round PAKE. Actually, if we allow ourselves to use SS-NIZK, we can construct a 1-round PAKE by combining our word-independent SPHF with the ideas in [23], which solves an open problem in [30]. Concretely, we use the first instantiation of [23], except that the ElGamal encryption scheme and its associated SPHF are replaced by our IND-CPA LWE-based encryption scheme à la Micciancio-Peikert and the word-independent SPHF is the one from Sect. 4. The SS-NIZK can be a simple variant of the one in [30]. Details are provided in the full version [6].
5.2 Honest-Verifier Zero-Knowledge
Following the methodology from [7], using our SPHF in Sect. 3, we can construct honest-verifier zero-knowledge proofs for any NP language of the form  where \(\ddot{\mathscr {R}}\) is a polynomial-size circuit. At a very high level, the prover simply encrypts each wire of the circuit using an IND-CPA encryption schemeFootnote 12 and then shows the correct evaluation at each gate, using SPHFs.
where \(\ddot{\mathscr {R}}\) is a polynomial-size circuit. At a very high level, the prover simply encrypts each wire of the circuit using an IND-CPA encryption schemeFootnote 12 and then shows the correct evaluation at each gate, using SPHFs.
For the sake of simplicity, we suppose that all gates of the circuit \(\ddot{\mathscr {R}}\) are NAND gates. We just need to construct an SPHF for the languages \(\widetilde{\mathscr {L}}\subseteq \mathscr {L}\) of ciphertexts \(C_{1},C_{2},C_{3}\) encrypting values \((b_1,b_2,b_3)\) so that \(b_3 = \text {NAND}(b_1,b_2)\), such that \(\widetilde{\mathscr {L}}\) is the set of encryptions of \(b_i\) that fits the NAND gate evaluation, while \(\mathscr {L}\) is the set of ciphertexts whose decryptions fit the gate evaluation. We can do that by combining our SPHFs using the classical techniques described in [2]. Details are provided in the full version [6].
5.3 Witness Encryption
Witness encryption [12] allows to encrypt a message, with respect to a particular word  and a language \(\mathscr {L}\), instead of using a classical public key. If the word is in the language, then a user knowing a witness for the word can decrypt the ciphertext, otherwise the ciphertext hides the message.
and a language \(\mathscr {L}\), instead of using a classical public key. If the word is in the language, then a user knowing a witness for the word can decrypt the ciphertext, otherwise the ciphertext hides the message.
An SPHF can be used to construct such a primitive as follows: To encrypt a message M with respect to a word  and a language \(\mathscr {L}\), use an SPHF for \(\mathscr {L}\) to generate a hashing key \(\mathsf {hk}\), a projection key \(\mathsf {hp}\), and a hash value \(\mathsf {H}\), and output the ciphertext \(C=(\mathsf {hp}, \mathsf {H}\oplus M)\). To decrypt such a ciphertext, simply use the witness
and a language \(\mathscr {L}\), use an SPHF for \(\mathscr {L}\) to generate a hashing key \(\mathsf {hk}\), a projection key \(\mathsf {hp}\), and a hash value \(\mathsf {H}\), and output the ciphertext \(C=(\mathsf {hp}, \mathsf {H}\oplus M)\). To decrypt such a ciphertext, simply use the witness  associated with the word
associated with the word  together with the projection key \(\mathsf {hp}\) to compute the projected hash value and recover M. Details are available in the full version [6].
together with the projection key \(\mathsf {hp}\) to compute the projected hash value and recover M. Details are available in the full version [6].
Notes
- 1.
- 2.
- 3.
More precisely, the probability of error is \({{\mathrm{poly}}}(n, \sigma )/q\), which is \({{\mathrm{negl}}}(n)\) for super-polynomial approximation factors \(q/\sigma \).
- 4.
The bound on \(\varvec{s}_1(\varvec{T})\) holds except with probability at most \(2^{-n}\) in the original construction, but for convenience we assume the algorithm restarts if it does not hold.
- 5.
This happens only with exponentially small probability \(2^{-\varTheta (n)}\) by Lemma 2.1.
- 6.
Note that the inversion algorithm \(g^{-1}_{(\cdot )}\) can succeed even if \(\Vert \varvec{e}\Vert > B'\), depending on the randomness of the trapdoor. It is crucial to reject decryption nevertheless when \(\Vert \varvec{e}\Vert > B'\) to ensure CCA2 security. We also recall that
 .
. - 7.
Contrary to previously known SPHFs, some of our SPHFs have randomized algorithms \(\mathsf {Hash}\) and \(\mathsf {ProjHash}\).
- 8.
Our definition of universality is equivalent to the one of Cramer and Shoup in [11], up to the use of language parameters.
- 9.
Of course, one could also obtain perfect universality by setting a constant rounding function \(r(x) = 1/2\), and even avoid the first harmonic, but there is no way to reach correctness even with amplification in that case.
- 10.
This is the smallest parameter \(\sigma \) for which LWE\(_{\chi , q}\) is known reduce to a worst-case problem. One may of course choose to use a different width for the LWE error, and derive different appropriate parameters.
- 11.
- 12.
We actually will use our IND-CCA2 encryption scheme à la Micciancio-Peikert.
References
Abdalla, M., Benhamouda, F., Pointcheval, D.: Public-key encryption indistinguishable under plaintext-checkable attacks. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 332–352. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_15
Abdalla, M., Chevalier, C., Pointcheval, D.: Smooth projective hashing for conditionally extractable commitments. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 671–689. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_39
Banaszczyk, W.: New bounds in some transference theorems in the geometry of numbers. Math. Ann. 296(1), 625–635 (1993)
Ben Hamouda, F., Blazy, O., Chevalier, C., Pointcheval, D., Vergnaud, D.: Efficient UC-secure authenticated key-exchange for algebraic languages. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 272–291. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36362-7_18
Benhamouda, F., Blazy, O., Chevalier, C., Pointcheval, D., Vergnaud, D.: New techniques for SPHFs and efficient one-round PAKE protocols. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 449–475. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_25
Benhamouda, F., Blazy, O., Ducas, L., Quach, W.: Hash proof systems over lattices revisited. Cryptology ePrint Archive, Report 2017/997 (2017). http://eprint.iacr.org/2017/997
Benhamouda, F., Couteau, G., Pointcheval, D., Wee, H.: Implicit zero-knowledge arguments and applications to the malicious setting. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part II. LNCS, vol. 9216, pp. 107–129. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_6
Boyen, X.: Attribute-based functional encryption on lattices. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 122–142. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_8
Cash, D., Hofheinz, D., Kiltz, E., Peikert, C.: Bonsai trees, or how to delegate a lattice basis. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 523–552. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_27
Cramer, R., Shoup, V.: A practical public key cryptosystem provably secure against adaptive chosen ciphertext attack. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 13–25. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055717
Cramer, R., Shoup, V.: Universal hash proofs and a paradigm for adaptive chosen ciphertext secure public-key encryption. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 45–64. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_4
Garg, S., Gentry, C., Sahai, A., Waters, B.: Witness encryption and its applications. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 467–476. ACM Press, June 2013
Gennaro, R., Lindell, Y.: A framework for password-based authenticated key exchange. ACM Trans. Inf. Syst. Secur. 9(2), 181–234 (2006)
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: Ladner, R.E., Dwork, C. (eds.) 40th ACM STOC, pp. 197–206. ACM Press, May 2008
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 545–554. ACM Press, June 2013
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Predicate encryption for circuits from LWE. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part II. LNCS, vol. 9216, pp. 503–523. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_25
Groce, A., Katz, J.: A new framework for efficient password-based authenticated key exchange. In: Al-Shaer, E., Keromytis, A.D., Shmatikov, V. (eds.) ACM CCS 10, pp. 516–525. ACM Press, October 2010
Halevi, S., Kalai, Y.T.: Smooth projective hashing and two-message oblivious transfer. J. Cryptol. 25(1), 158–193 (2012)
Jiang, S., Gong, G.: Password based key exchange with mutual authentication. In: Handschuh, H., Hasan, M.A. (eds.) SAC 2004. LNCS, vol. 3357, pp. 267–279. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30564-4_19
Jutla, C., Roy, A.: Relatively-sound NIZKs and password-based key-exchange. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 485–503. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-30057-8_29
Kalai, Y.T.: Smooth projective hashing and two-message oblivious transfer. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 78–95. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_5
Katz, J., Vaikuntanathan, V.: Smooth projective hashing and password-based authenticated key exchange from lattices. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 636–652. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_37
Katz, J., Vaikuntanathan, V.: Round-optimal password-based authenticated key exchange. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 293–310. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_18
Lyubashevsky, V.: Lattice-based identification schemes secure under active attacks. In: Cramer, R. (ed.) PKC 2008. LNCS, vol. 4939, pp. 162–179. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78440-1_10
Lyubashevsky, V.: Fiat-Shamir with aborts: applications to lattice and factoring-based signatures. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 598–616. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_35
Majewski, B.S., Havas, G.: The complexity of greatest common divisor computations. In: Adleman, L.M., Huang, M.-D. (eds.) ANTS 1994. LNCS, vol. 877, pp. 184–193. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-58691-1_56
Micciancio, D., Peikert, C.: Trapdoors for lattices: simpler, tighter, faster, smaller. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 700–718. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_41
Micciancio, D., Regev, O.: Worst-case to average-case reductions based on Gaussian measures. In: 45th FOCS, pp. 372–381. IEEE Computer Society Press, October 2004
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Gabow, H.N., Fagin, R. (eds.) 37th ACM STOC, pp. 84–93. ACM Press, May 2005
Zhang, J., Yu, Y.: Two-round PAKE from approximate SPH and instantiations from lattices. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017, Part III. LNCS, vol. 10626, pp. 37–67. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70700-6_2
Acknowledgments
We would like to sincerely thank Zvika Brakerski for many useful and interesting discussions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Benhamouda, F., Blazy, O., Ducas, L., Quach, W. (2018). Hash Proof Systems over Lattices Revisited. In: Abdalla, M., Dahab, R. (eds) Public-Key Cryptography – PKC 2018. PKC 2018. Lecture Notes in Computer Science(), vol 10770. Springer, Cham. https://doi.org/10.1007/978-3-319-76581-5_22
Download citation
DOI: https://doi.org/10.1007/978-3-319-76581-5_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-76580-8
Online ISBN: 978-3-319-76581-5
eBook Packages: Computer ScienceComputer Science (R0)








 , and
, and  . Let
. Let 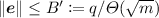 , then
, then 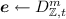 where
where  .
. derives a projection key
derives a projection key  ;
; outputs a hash value
outputs a hash value  and the language parameter
and the language parameter  outputs a projected hash value
outputs a projected hash value  , for the word
, for the word  (i.e.,
(i.e., 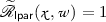 ) and the language parameter
) and the language parameter  , with overwhelming probability over the randomness of
, with overwhelming probability over the randomness of  (and associated witness
(and associated witness  ), the value
), the value  is approximately determined by
is approximately determined by 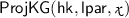 relative to the Hamming metric. More precisely, writing
relative to the Hamming metric. More precisely, writing 
 and the random coins of
and the random coins of 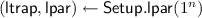 , with overwhelming probability over the randomness of
, with overwhelming probability over the randomness of 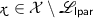 the following distributions have statistical distance negligible in n:
the following distributions have statistical distance negligible in n: 
 , with overwhelming probability over the randomness of
, with overwhelming probability over the randomness of  :
: 
 and the random coins of
and the random coins of  , with overwhelming probability over the randomness of
, with overwhelming probability over the randomness of 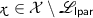 , any projection key
, any projection key 
 and the random coins of
and the random coins of  ;
; .
.