A Formal Model for Multi SPLs

Abstract

A Software Product Line (SPL) is a family of similar programs generated from a common artifact base. A Multi SPL (MPL) is a set of interdependent SPLs that are typically managed and developed in a decentralized fashion. Delta-Oriented Programming (DOP) is a flexible and modular approach to implement SPLs. This paper presents new concepts that extend DOP to support the implementation of MPLs. These extensions aim to accommodate compositional analyses. They are presented by means of a core calculus for delta-oriented MPLs of Java programs. Suitability for MPL compositional analyses is demonstrated by compositional reuse of existing SPL analysis techniques.

This work has been partially supported by: EU Horizon 2020 project HyVar (www.hyvar-project.eu), GA No. 644298; ICT COST Action IC1402 ARVI (www.cost-arvi.eu); and Ateneo/CSP D16D15000360005 project RunVar (runvar-project.di.unito.it).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Highly-configurable software systems can be described as Software Product Lines (SPLs). An SPL is a family of similar programs, called variants, that have a well-documented variability and are generated from a common artifact base [2, 7, 19]. An SPL consists of: (i) a feature model defining the set of variants in terms of features (each feature represents an abstract description of functionality and each variant is identified by a set of features, called a product); (ii) an artifact base providing language dependent reusable code artifacts that are used to build the variants; and (iii) configuration knowledge which connects feature model and artifact base by defining how to derive variants from the code artifacts given the products (thus inducing a mapping from products to variants, called the generator of the SPL).

Delta-Oriented Programming (DOP) [2, Sect. 6.6.1], [21] is a flexible and modular approach to implement SPLs. The artifact base of a delta-oriented SPL consists of a base program (that might be empty) and of a set of delta modules (deltas for short), which are containers of modifications to a program (e.g., for Java programs, a delta can add, remove or modify classes and interfaces). The configuration knowledge of a delta-oriented SPL defines the generator by associating to each delta an activation condition over the features (i.e., a set of products) and specifying an application ordering between deltas. DOP supports the automatic generation of variants based on a selection of features: once a user selects a product, the corresponding variant is derived by applying the deltas with a satisfied activation condition to the base program according to the application ordering. Moreover, DOP is a generalization of Feature-Oriented Programming (FOP) [2, Sect. 6.1], [4] a previously proposed approach to implement SPLs where deltas correspond one-to-one to features and do not contain remove operations.

Modern software systems often out-grow the scale of SPLs by involving the notion of Multi SPLs (MPLs), i.e., sets of interdependent SPLs that need to be managed in a decentralized fashion by multiple teams and stakeholders [13]. There are two main motivations to build such MPLs: either to structure a complex SPL into more manageable modules, or to reuse existing SPLs into a bigger project. In this paper we give, to the best of our knowledge, the first formal model of MPLs that spans feature model, artifact base and configuration knowledge. Our model is constructed around the concepts of SPL signature, Dependent SPL and SPL composition. It builds on recent work done by Schröter et al. [24] on compositional analysis of feature models, and on the delta-oriented programming core calculus IF$\varDelta$J by Bettini et al. [5], which is extended here to enable the construction of MPLs. The main achievement of our model is the ability to modularly compose and analyze SPLs by means of Dependent SPLs, which are SPLs with explicit dependencies, modeled by SPL signatures, that can be filled by SPLs (or Dependent SPLs) satisfying the given signatures.

Section 2 provides some background. Section 3 formalizes the main concepts proposed in the paper by introducing the Imperative Featherweight Multi Delta Java (IFM$\varDelta$J) calculus, which extends IF$\varDelta$J to implement MPLs. Section 4 illustrates how the concepts of SPL signature, dependent SPL, and SPL composition support compositionality of existing SPL analysis, like feature model analysis or type checking. Section 5 discusses related work.

2 Background and Running Example

2.1 IF$\varDelta$J: A Formal Foundation for Delta-Oriented SPLs

IF$\varDelta$J [5] is a core calculus for delta-oriented SPLs where variants are written in IFJ (an imperative version of FJ [14]). The abstract syntax of IFJ is given in Fig. 1 (explanations are given in the caption)—following [14], we use the overline notation for (possibly empty) sequences of elements: for instance $\overline{e}$ stands for a sequence of expressions. The empty sequence is denoted by $\emptyset$. Type system, operational semantics, and type soundness for IFJ are given in [5].

The abstract syntax of IF$\varDelta$J SPLs is given in Fig. 2 (explanations are given in the caption). The deltas in the artifact base must have distinct names, the class operations in a delta must act on distinct classes, and the attribute operations in a class operation must act on distinct attributes. In IF$\varDelta$J there is no concrete syntax for the feature model and the configuration knowledge. As usual, to simplify the formalization, we represent feature models $\mathcal {M}$ as pairs (set of features, set of products) and configuration knowledges $\mathcal {K}$ as pairs (mapping from deltas to activation conditions, delta application ordering).

Fig. 1.

Syntax of IFJ. A program P is a sequence of class declarations $\overline{CD}$. A class declaration comprises the name C of the class, the name of the superclass (which must always be specified, even if it is the built-in class $\texttt {Object}$), and a list of attribute (field or method) declarations $\overline{AD}$. Variables x include the special variable this (implicitly bound in any method declaration MD), which may not be used as the name of a method’s formal parameter. All fields and methods are public, there is no field shadowing, there is no method overloading, and each class is assumed to have an implicit constructor that initialized all fields to null. The subtyping relation $\mathrel {{<}{:}}$ on classes, which is the reflexive and transitive closure of the immediate subclass relation (given by the extends clauses in class declarations), is supposed to be acyclic.

Fig. 2.

Syntax of IF $\varDelta$ J SPLs. An SPL declaration comprises the name $\texttt {L}$ of the product line, a feature model $\mathcal {M}$, configuration knowledge $\mathcal {K}$, and an artifact base AB. The artifact base comprises a (possibly empty) IFJ program P, and a set of deltas $\overline{DD}$. A delta declaration DD comprises the name $\texttt {d}$ of the delta and class operations $\overline{CO}$ representing the transformations performed when the delta is applied to an IFJ program. A class operation can add, remove, or modify a class. A class can be modified by (possibly) changing its super class and performing attribute operations $\overline{AO}$ on its body. An attribute name a is either a field name ${\texttt {f}}$ or a method name $\texttt {m}$. An attribute operation can add or remove fields and methods, and modify the implementation of a method by replacing its body. The new body may call the special method $\texttt {original}$, which is implicitly bound to the previous implementation of the method and may not be used as the name of a method.

Definition 1

(Feature model). A feature model $\mathcal {M}_x$ is a pair $(\mathcal {F}_x,\mathcal {P}_x)$ where $\mathcal {F}_x$ is a set of features and $\mathcal {P}_x\subseteq 2^{\mathcal {F}_x}$ is a set of products. $\mathcal {M}_{\emptyset } = (\emptyset ,\emptyset )$ is the empty feature model.

Definition 2

(Configuration knowledge). A configuration knowledge $\mathcal {K}_x$ is a pair $(\alpha _x,<_x)$ where $\alpha _x$ is a map that associates to each delta declaration the set of products that activate it (the activation condition), and $<_x$ is an ordering between deltas (the application ordering).

These representations simplify stating and proving results independently from implementation details. However, they do not scale well in actual implementations. In the examples, we represent feature models also as feature diagrams (which are diagrams that illustrate feature dependencies by organizing features in a tree structure with cross tree-constraints) or as propositional formulas $\varPhi$ where variables are feature names $\textit{f}$ (see, e.g., [3] for a discussion on other possible representations):

$$\begin{aligned} \varPhi \,{::}\!\!=\,\mathbf{true}\,\, | \,\,f \,\, |\,\, \varPhi \, \Rightarrow \, \varPhi \,\,|\,\,\lnot \varPhi \,\,|\,\,\varPhi \wedge \varPhi \,\,|\,\,\varPhi \vee \varPhi \end{aligned}$$

To avoid over-specification, the ordering $<_x$ may be partial. We assume unambiguity of the SPL, i.e., for each product, any total ordering of the activated deltas that respects $<_x$ generates the same variant (see [5, 18] for effective means to ensure unambiguity). In examples, we represent activation conditions as propositional formulas (see above) and application orderings as total orderings on a partition of the set of delta names.

Feature model, configuration knowledge and artifact base of an SPL named $\mathtt {L}$ are denoted by $\mathcal {M}_\mathtt {L}=(\mathcal {F}_\mathtt {L},\mathcal {P}_\mathtt {L})$, $\mathcal {K}_\mathtt {L}=(\alpha _\mathtt {L},<_\mathtt {L})$ and $AB_\mathtt {L}$, respectively. In order to define the generator $\mathcal {G}_\mathtt {L}$ of an SPL $\mathtt {L}$, we first introduce the auxiliary notions of delta applicability and delta application. A delta $\mathtt {d}$ is applicable to a program ${ P}$ iff each class to be added does not exist; each class to be removed or modified exists; and (for every class-modify operation): each method or field to be added does not exist; each method or field to be removed exists; each method to be modified exists and has the same header specified in the method-modify operation. If $\mathtt {d}$ is applicable to ${ P}$, then the application of $\mathtt {d}$ to ${ P}$ is the program, denoted by $\mathtt {d}({ P})$, obtained from ${ P}$ by applying all the operations in $\mathtt {d}$—otherwise $\mathtt {d}({ P})$ is undefined.

Definition 3

(Generator of an SPL [5]). The generator of $\mathtt {L}$, denoted by $\mathcal {G}_\mathtt {L}$, is the mapping that associates each product p of $\mathtt {L}$ to the IFJ program $\mathtt {d}_n(\cdots$ $\mathtt {d}_1({ P})\cdots )$, where ${ P}$ is the base program of $\mathtt {L}$ and $\mathtt {d}_1\ldots ,\mathtt {d}_n$ $(n \ge 0)$ are the deltas of $\mathtt {L}$ activated by p, listed according to the application order.

Fig. 3.

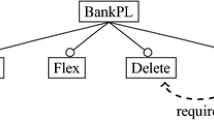
Left: CapitalAccount SPL: feature model $\mathcal {M}_{\textsf {CapitalAccount}}$ (top), configuration knowledge $\mathcal {K}_{\textsf {CapitalAccount}}$ (middle), and artifact base $\textit{AB}_{\textsf {CapitalAccount}}$ (bottom). This SPL provides a class CapAccount for money managing bank accounts. The mandatory feature BalanceInfo provides some basic fields (identity, balance and lastUpdate) and a method withdraw (method deposit, which is similar, is omitted). InterestRate and YearlyFees provide two alternative bank-policies: one and only one of them, must be selected. The former manages accrued interests and operation-fees (applied to each withdraw), the second manages fixed fees per year (and no bank interests). The optional feaure Overdraft, which allows to withdraw more money than that available, requires feaure InterestRate in order to apply a negative interest. Right: FinancialAccount SPL: $\mathcal {M}_{\textsf {FinancialAccount}}$ (top), $\mathcal {K}_{\textsf {FinancialAccount}}$ (middle), and $\textit{AB}_{\textsf {FinancialAccount}}$ (bottom). This SPL provides a class FinAccount for investment product managing bank accounts. The mandatory feature AmountInfo provides basic fields (identity, liquidity). It must be flanked by at least one feature between Portfolio and Welfare. The latter provides a list of welfare products. The former provides a list of financial products.

The generator $\mathcal {G}_\mathtt {L}$ may be partial since, for some product of $\mathtt {L}$, a delta $\textit{DD}_i$ $(1\le i\le n)$ may not be applicable to the intermediate variant $\textit{DD}_{i-1}(\cdots$ $\textit{DD}_1({ P})\cdots )$ thus making $\mathcal {G}_\mathtt {L}$ undefined for that product.

The running example of this paper is based on bank accounts. Figure 3 illustrates an SPL of capital accounts (CapitalAccount, on the left) and an SPL of financial accounts (FinancialAccount, on the right)—explanations are given in the caption. To make the example more readable, in the artifact bases we use Java syntax for field initialization, primitive data types, strings and sequential composition—encoding in IF$\varDelta$J syntax is straightforward (see [5]).

Remark 1

(Base program and empty product). In order to simplify the presentation, the formal definitions in the rest of this document assume that: (i) the base program is always the empty program; (ii) no delta $\mathtt {d}$ is activated by the empty product (i.e., $\emptyset \not \in \alpha _{\mathtt {L}}(\mathtt {d})$ for all $\mathtt {d}$); and (iii) $\mathcal {G}_\mathtt {L}(\emptyset )=\emptyset$, even when $\emptyset$ is not a product. Note that these assumptions are not restrictive. In particular, the base program of any SPL $\mathtt {L}$ can be always encoded as an extra delta (the base delta) with distinguished name $\mathtt {d}_\mathtt {L}$ such that $\alpha _\mathtt {L}(\mathtt {d}_\mathtt {L})=\mathcal {P}_\mathtt {L}$ and $\mathtt {d}_\mathtt {L}$ is the minimum according to $<_\mathtt {L}$.

2.2 Feature Model Composition and Feature Model Interfaces

Recently, Schröter et al. [24] considered a notion of feature model composition through aggregation (i.e., by inclusion of one feature model into another feature model [20]) and proposed to use it in combination with a notion of feature model interface in order to support compositional analyses of feature models.

Definition 4

(Feature model composition [24]). Let $\mathcal {M}_x=(\mathcal {F}_x, \mathcal {P}_x)$, $\mathcal {M}_y=(\mathcal {F}_y, \mathcal {P}_y)$, and $\mathcal {M}_{\textit{Glue}}=(\mathcal {F}_{\textit{Glue}}, \mathcal {P}_{\textit{Glue}})$ be feature models that satisfy the glue-proviso $\mathcal {F}_{\textit{Glue}}\subseteq \mathcal {F}_x\cup \mathcal {F}_y$. The composition of $\mathcal {M}_x$ and $\mathcal {M}_y$ is the feature model, denoted as $\mathcal {M}_{x/y}$, defined as follows by using composition operation $\circ$, the auxiliary join operation $\bullet$, and the auxiliary operation $\mathcal {R}$:

$$\begin{array}{rcl} \mathcal {M}_{x/y} &{} = &{} \circ (\mathcal {M}_x, \mathcal {M}_y, \mathcal {M}_{\textit{Glue}}) = \mathcal {M}_x \circ _{\mathcal {M}_{\textit{Glue}}} \mathcal {M}_y = (\mathcal {M}_x \bullet \mathcal {R}(\mathcal {M}_y)) \bullet \mathcal {M}_{\textit{Glue}} \\ \mathcal {R}(\mathcal {M}_y) &{} = &{} (\mathcal {F}_y , \mathcal {P}_y \cup \{\emptyset \}) \\ \mathcal {M}_x \bullet \mathcal {M}_y &{} = &{} (\mathcal {F}_x \cup \mathcal {F}_y , \{p \cup q \, |\, p \in \mathcal {P}_x, q \in \mathcal {P}_y , p \cap \mathcal {F}_y = q \cap \mathcal {F}_x \}) \end{array}$$

Operation $\mathcal {R}$ takes one feature model $\mathcal {M}_y$ as input and converts it to a new feature model in which the empty product is a valid product (thus $\mathcal {P}_y$ core features are not necessarily core in the composed feature model). Operation $\bullet$ is similar to a cross product from relational algebra and creates all combinations between both product sets.

The feature model $\mathcal {M}_{\textit{Glue}}$ describes a parent-child relationship and other constraints between $\mathcal {M}_x$ and $\mathcal {M}_y$ in order to connect them.

Definition 5

(Feature model interface [24]). A feature model $\mathcal {M}_{\textit{Int}}=(\mathcal {F}_{\textit{Int}},$ $\mathcal {P}_{\textit{Int}})$ is an interface of feature model $\mathcal {M}_x=(\mathcal {F}_x,\mathcal {P}_x)$, denoted as $\mathcal {M}_{\textit{Int}}\preceq \mathcal {M}_x$, iff $\mathcal {F}_{\textit{Int}}\subseteq \mathcal {F}_x$ and $\mathcal {P}_{\textit{Int}}=\{p\cap \mathcal {F}_{\textit{Int}} |p\in \mathcal {P}_x\}$.

Remark 2

(Feature disjointness). As pointed out in [24, Sect. 4.1, second to last paragraph] the compositional results about $\circ$ “are based on the assumption that $\mathcal {F}_x$ and $\mathcal {F}_y$ do not share features (i.e. $\mathcal {F}_x\cap \mathcal {F}_y=\emptyset$)”. In the rest of this document, the use of $\circ$ always relies on this feature disjointedness assumption.

3 IFM$\varDelta$J: A Core Calculus for MPLs

The example presented in Fig. 3 introduces two SPLs, CapitalAccount and FinancialAccount, describing two kinds of bank accounts: it would make perfect sense to combine these two SPLs in order to obtain an SPL describing a bank account with functionalities described in both SPLs.

In a first approach, one could define a new SPL DualAccount that uses (i.e., depends on) the two bank account SPLs presented in Fig. 3 to define a new class that implements the different features defined in the two SPLs. We call an SPL with such dependencies a Dependent SPL. However, such an approach is not satisfactory as it couples too strongly DualAccount to its SPLs: DualAccount is set to use the CapitalAccount and FinancialAccount SPLs and cannot change even if a more efficient implementation of these SPLs comes up. To deal with this issue, we introduce the notion of SPL signature which is used to specify the APIs on which a Dependent SPL depends; then any SPL that implements such signature can fulfill the dependencies of a Dependent SPL.

Hence, our approach to define the DualAccount Dependent SPL follows the structure presented on the right: DualAccount depends on two SPL signatures: CapAccInt specifies the API requested by DualAccount for the capital account backend implementation, while FinAccInt specifies the API requested by DualAccount for the financial account implementation. Then these two signatures are implemented by CapitalAccount and FinancialAccount respectively, and possibly other SPLs.

We structure the presentation of our model as follows: first we introduce the concept of SPL signature (SPLS) and formally define when an SPL implements an SPL signature; second we define the notion of Dependent SPL (DPL) as we just presented; and finally, we demonstrate how to generate the variants of a DPL.

Fig. 4.

Syntax of IFM $\varDelta$ J. Program signatures (top). SPL signature declarations (middle). Dependent SPL declarations (bottom)—the extensions with respect to IF$\varDelta$J SPLs (given in Fig. 2, with the syntax of artifact bases $\textit{AB}$) are highlighted in grey.

3.1 SPL Signatures

An SPL signature (SPLS) describes the API of an SPL and is structured like an SPL with a feature model, configuration knowledge, and an artifact base. Its difference with an SPL lies in the fact that its artifact base does not include the implementation of methods. Figure 4 (middle) gives the abstract syntax of SPLSs which uses program signatures, presented in Fig. 4 (top), to construct their artifact bases. A program signature is a program deprived of method bodies. An SPLS declaration LS comprises the name $\mathtt {Z}$ of the SPLS, a feature model $\mathcal {M}$, configuration knowledge $\mathcal {K}$ and an artifact base signature ABS which, in turn, comprises a program signature PS and a set of delta signatures $\overline{DS}$—a delta signature DS is a delta deprived of method-modifies operations and method bodies.

An SPL $\mathtt {L}$ implements an SPLS $\mathtt {Z}$ when all the declarations in $\mathtt {Z}$ are implemented in $\mathtt {L}$. I.e., when all the products of $\mathtt {Z}$ can be extended in a product of $\mathtt {L}$ and for each variant of $\mathtt {Z}$, all of its declared elements are implemented in the corresponding variant of $\mathtt {L}$. We first define the generator of an SPLS (in order to define what are its variants and their declaration), and then present the definition of the interface relation, defining when an SPL implements an SPLS.

Definition 6

(Generator of an SPLS). The generator of an SPLS $\mathtt {Z}$, denoted by $\mathcal {G}_{\mathtt {Z}}$, is a mapping from products to program signatures defined similarly to the generator of an SPL (see Definition 3).

Definition 7

(Program interface). A program signature $PS_{\textit{Int}}$ is an interface of program P, denoted as $PS_{\textit{Int}}\preceq P$, iff $PS_{\textit{Int}}$ is obtained from P by dropping some class or attributes, the body of the remaining methods and by replacing some ${{\mathbf {\mathsf{{extends}}}}}$  $\mathtt {C} \, clause \, by \,$ extends $\mathtt {C'}$ $\, where\,$ $\mathtt {C'}$ $\,\, is \, a \, superclass \, of \,$ $\mathtt {C}$.

Fig. 5.

Left: CapAccInt SPLS: $\mathcal {M}_{\textsf {CapAccInt}}$ (top), $\mathcal {K}_{\textsf {CapAccInt}}$ (middle), and $AB_{\textsf {CapAccInt}}$ (bottom). This SPLS is an interface of the CapitalAccount SPL if Fig. 3 (left). It hides features BalanceInfo and YearlyFees. Right: FinAccInt SPLS: $\mathcal {M}_{\textsf {FinAccInt}}$ (top), $\mathcal {K}_{\textsf {FinAccInt}}$ (middle), and $AB_{\textsf {FinAccInt}}$ (bottom). This SPLS is an interface of the FinancialAccount SPL of Fig. 3 (right). It hides feature AmountInfo.

Definition 8

(SPL interface). An SPLS $\mathtt {Z}_{\textit{Int}}$ is an interface of an SPL $\mathtt {L}$, denoted as $\mathtt {Z}_{\textit{Int}}\preceq \mathtt {L}$, iff: (i) $\mathcal {M}_{\mathtt {Z}_{\textit{Int}}}\preceq \mathcal {M}_{\mathtt {L}}$; and (ii) the generators $\mathcal {G}_{\mathtt {Z}_{\textit{Int}}}$ and $\mathcal {G}_{\mathtt {L}}$ are total and for each $p\in \mathcal {P}_{\mathtt {L}}$, $\mathcal {G}_{\mathtt {Z}_{\textit{Int}}}(p\cap \mathcal {F}_{\mathtt {Z}_{\textit{Int}}})\preceq \mathcal {G}_{\mathtt {L}}(p)$.

We say that an SPL $\mathtt {L}$ implements an SPLS $\mathtt {Z}$ when $\mathtt {Z}$ is an interface of $\mathtt {L}$.

Figure 5 represents an interface of SPL CapitalAccount (CapAccInt, on the left) and an interface of SPL FinancialAccount (FinAccInt, on the right), explanations are given in the caption.

3.2 Dependent SPLs

A Dependent SPL (DPL) is an SPL extended with dependencies modeled by SPLSs. The abstract syntax of IFM$\varDelta$J DPLs is given in Fig. 4 (bottom). A DPL declaration comprises the name $\mathtt {L}$ of the DPL, a sequence of SPLS names $\overline{\mathtt {Z}}=\mathtt {Z}_1,\dots ,\mathtt {Z}_n$ specifying its dependencies, a pair of feature models $\mathcal {M}_{\textit{Main}}$ and $\mathcal {M}_{\textit{Glue}}$, configuration knowledge $\mathcal {K}$ and an artifact base $\textit{AB}$. The two feature models $\mathcal {M}_{\textit{Main}}$ and $\mathcal {M}_{\textit{Glue}}$ structure the actual feature model $\mathcal {M}_\mathtt {L}$ of $\mathtt {L}$ in two parts: $\mathcal {M}_{\textit{Main}}$ describes the part of $\mathcal {M}_\mathtt {L}$ that is local to $\mathtt {L}$, while $\mathcal {M}_{\textit{Glue}}$ states how the features of $\mathcal {M}_\mathtt {L}$ are related with the features of $\mathtt {L}$’s dependencies. Formally, the feature model of $\mathtt {L}$ is defined as a composition of $\mathcal {M}_{\textit{Main}}$ and the feature models $\mathcal {M}_{\mathtt {Z}_1},\dots ,\mathcal {M}_{\mathtt {Z}_n}$, glued together with $\mathcal {M}_{\textit{Glue}}$: $\mathcal {M}_\mathtt {L}=\mathcal {M}_{\textit{Main}/\overline{\mathtt {Z}}}=\mathcal {M}_{\textit{Main}} \circ _{\mathcal {M}_{\textit{Glue}}} \mathcal {M}_{\overline{\mathtt {Z}}}$ where $\mathcal {M}_{\overline{\mathtt {Z}}}=\mathcal {R}(\mathcal {M}_{\mathtt {Z}_1})$ $\bullet$ $\cdots$ $\bullet$ $\mathcal {R}(\mathcal {M}_{\mathtt {Z}_n})$. Lemma 1 below guarantees that the order of $\mathtt {Z}_1$,...,$\mathtt {Z}_n$ is immaterial.

Lemma 1

(Join operation). The join operation $\bullet$ is associative and commutative, with $\mathcal {M}_{ Id }= \mathcal {R}(\mathcal {M}_\emptyset )=\mathcal {R}((\emptyset ,\emptyset ))=(\emptyset ,\{\emptyset \})$ as identity.

Figure 6 presents the DPL DualAccount with dependencies CapAccInt and FinAccInt —explanations are given in the caption.

Remark 3

(DPL conservatively extends SPL). In order to ensure that the concept of DPL is a conservative extension of the concept of SPL (cf. Sect. 2.1), we assume that if a DPL $\mathtt {L}$ has no dependencies (i.e., $\overline{\mathtt {Z}}=\emptyset$) then $\mathcal {M}_{\textit{Glue}}=\mathcal {M}_{ Id }$ (cf. Lemma 1). Therefore: (i) any DPL $\mathtt {L}$ without dependencies can be seen as an SPL with feature model $\mathcal {M}_\mathtt {L}=\mathcal {M}_{\textit{Main}}$; and (ii) any SPL $\mathtt {L}$ can be seen as a DPL with $\mathcal {M}_{\textit{Main}}=\mathcal {M}_\mathtt {L}$ and $\mathcal {M}_{\textit{Glue}}=\mathcal {M}_{ Id }$.

Definition 9

(Multi Software Product Lines). A Multi Software Product Line (MPL) is a set of SPL Signatures and Dependent SPLs.

Sanity Conditions. To simplify the manipulation of our model in the rest of the document, we give here a set of standard sanity conditions that are supposed to be satisfied by the MPLs that we consider in this paper. First, we suppose that all the DPL and SPLS names used in an MPL are declared exactly once in the MPL. Second, we suppose that a DPL depends only once on an SPLS, i.e., the list of dependencies $(\overline{\mathtt {Z}})$ in the DPL syntax does not contain duplicates. Finally, we suppose that a class can only be declared and modified by at most one DPL in an MPL. Note that class disjointness enforces a boundary between different DPLs and rules out class name clashes between variants of different DPLs. Moreover, without loss of generality, we assume that the scope of the name of a delta is limited to the DPL or SPLS that contain its declaration (i.e., each delta name may belong to a unique DPL or SPLS).

3.3 DPLs Composition

The concept of DPL-SPLs composition formalizes composition of software product lines through aggregation by means of the concepts of DPL and SPL interface (i.e., by inclusion of some SPLs into a DPL to fulfill its dependencies)—thus extending the concept of feature model composition to encompass the configuration knowledge and the artifact base.

Fig. 6.

DualAccount DPL is declared as:                                                                   line DualAccount(CapAccInt,FinAccInt) {$\mathcal {M}_{\textit{Main}_{\textsf {DualAccount}}}$ $\mathcal {M}_{\textit{Glue}_{\textsf {DualAccount}}}$ $\mathcal {K}_{\textsf {DualAccount}}$ $\textit{AB}_{\textsf {DualAccount}}$}. It has feature model $\mathcal {M}_{\textsf {DualAccount}}$ $=$ $\mathcal {M}_{\textit{Main}_{\textsf {DualAccount}}/\textsf {CapAccInt},\textsf {FinAccInt}}=\mathcal {M}_{\textit{Main}_{\textsf {DualAccount}}}\circ _{\mathcal {M}_{\textit{Glue}_{\textsf {DualAccount}}}} \mathcal {M}_{\textsf {CapAccInt},\textsf {FinAccInt}}$ (depicted as a feature diagram at the top of the figure); configuration knowledge $\mathcal {K}_{\textsf {DualAccount}}$ (middle); and artifact base $\textit{AB}_{\textsf {DualAccount}}$ (bottom). It provides a class DualAccount that combines two bank accounts that satisfy the dependencies CapAccInt and FinAccInt (given in Fig. 5), respectively. The feature model $\mathcal {M}_{\textsf {DualAccount}}$ is the composition of four feature models. (i) The feature model $\mathcal {M}_{\textit{Main}_{\textsf {DualAccount}}}$, which comprises the mandatory feature DualAccount and the optional feature LogBook (that ensures that transactions are traced). (ii)-(iii) The feature models of the dependencies CapAccInt and FinAccInt (given in Fig. 5). (iv) The feature model $\mathcal {M}_{\textit{Glue}_{\textsf {DualAccount}}}$, which has features DualAccount, LogBook, CapitalAccount,FinancialAccount, InterestRate, Portfolio and expresses the constraints $\textsf {FinancialAccount}\vee \textsf {CapitalAccount}$, $\textsf {CapitalAccount}\rightarrow \textsf {InterestRate}$ $\textsf {FinancialAccount}\rightarrow \textsf {Portfolio}$ (represented by the parts colored in red of the feature diagram) and $\textsf {CapitalAccount}\wedge \textsf {FinancialAccount} \rightarrow \textsf {LogBook}$ (represented by the cross-tree constraint, also colored in red). The dashed rectangles depict the feature diagrams representing the feature model obtained from $\mathcal {M}_{\textsf {CapAccInt}}$ and $\mathcal {M}_{\textsf {FinAccInt}}$ by adding the constraints provided by the feature model $\mathcal {M}_{\textit{Glue}_{\textsf {DualAccount}}}$, respectively. (color figure online)

Definition 10

(DPL-SPLs composition). Let $\mathtt {L}$ be a DPL with dependencies $\overline{\mathtt {Z}}=\mathtt {Z}_1,...,\mathtt {Z}_n$ ($n\ge 0$) and $\overline{\mathtt {L}}=\mathtt {L}_1,...,\mathtt {L}_n$ be SPLs such that $\mathtt {Z}_i\preceq \mathtt {L}_i$ ($1\le i\le n)$. The composition of $\mathtt {L}$ with $\overline{\mathtt {L}}$ is the SPL (cf. Remark 3) $\mathtt {L}_{0}=\mathtt {L}(\overline{\mathtt {L}})$ such that:¹

• $\mathcal {M}_{ Main _{\mathtt {L}_{0}}}=\mathcal {M}_{ Main _\mathtt {L}/\overline{\mathtt {L}}}=\mathcal {M}_{ Main _\mathtt {L}} \circ _{\mathcal {M}_{ Glue _\mathtt {L}}} \mathcal {M}_{\overline{\mathtt {L}}}$ ;

• $\mathcal {K}_{\mathtt {L}_{0}} = (\alpha _{\mathtt {L}_{0}},<_{\mathtt {L}_{0}}) = (\alpha '_{\mathtt {L}}\cup \big (\bigcup _{i\in \{1,...,n\}}\alpha '_{\mathtt {L}_i}\big ),<_{\mathtt {L}}\cup \big (\bigcup _{i\in \{1,...,n\}}<_{\mathtt {L}_i}\big ))$ where

  –:

  $\alpha '_{\mathtt {L}}(\mathtt {d})=\{p\in \mathcal {P}_{\mathtt {L}_{0}} \;|\;$ $p\cap \mathcal {F}_{\mathtt {L}}\in \alpha _{\mathtt {L}}(\mathtt {d})\}$ for all deltas $\mathtt {d}$ of $\mathtt {L}$;

  –:

  $\alpha '_{\mathtt {L}_i}(\mathtt {d})=\{p\in \mathcal {P}_{\mathtt {L}_{0}} \;|\;$ $p\cap \mathcal {F}_{\mathtt {L}_i}\in \alpha _{\mathtt {L}_i}(\mathtt {d})\}$ for all deltas $\mathtt {d}$ of $\mathtt {L}_i$;

• $\textit{AB}_{\mathtt {L}_{0}}=\textit{AB}_{\mathtt {L}}\cup \big (\bigcup _{i\in \{1,...,n\}}\textit{AB}_{\mathtt {L}_i}\big )$; and

• $\mathcal {M}_{ Glue _{\mathtt {L}_{0}}}=\mathcal {M}_{ Id }$.

Note that, if $\mathtt {L}$ has no dependencies (i.e., $n=0$), then $\mathcal {G}_{\mathtt {L}(\overline{\mathtt {L}})}=\mathcal {G}_{\mathtt {L}(\emptyset )}=\mathcal {G}_\mathtt {L}$ (so, $\mathtt {L}(\overline{\mathtt {L}})$ and $\mathtt {L}$ have the same variants). For example, the DPL DualAccount can be composed with the SPLs CapitalAccount and FinancialAccount to obtain the SPL DualAccount(CapitalAccount,FinancialAccount).

The following theorems shed light on DPL-SPLs composition. Theorem  1 states that the variants of the composed SPL $\mathtt {L}(\overline{\mathtt {L}})$ can be generated by building the composed feature model $\mathcal {M}_{\mathtt {L}(\overline{\mathtt {L}})}$ and then using the generators of the DPL $\mathtt {L}$ and of the SPLs $\overline{\mathtt {L}}$—thus, there is no need to actually build the whole $\mathtt {L}(\overline{\mathtt {L}})$. Theorem 2 states that fulfilling the dependencies of a DPL preserves the set of implemented interfaces.

Theorem 1

(Generator of the composed product line). Let $\mathtt {L}_{0}=\mathtt {L}(\overline{\mathtt {L}})$. For each product $p\in \mathcal {P}_{\mathtt {L}_{0}}$, $\mathcal {G}_{\mathtt {L}_{0}}(p) = \mathcal {G}_{\mathtt {L}}(p\cap \mathcal {F}_{\mathtt {L}})\cup \big (\bigcup _{\mathtt {L}_i\in \overline{\mathtt {L}} }\mathcal {G}_{\mathtt {L}_i}(p\cap \mathcal {F}_{\mathtt {L}_{i}})\big )$.

Theorem 2

(DPL-SPLs composition preserves interfacing). Let $\mathtt {Z}$ be an SPLS, $\mathtt {L}$ be a DPL with dependencies $\overline{\mathtt {Z}}=\mathtt {Z}_1,...,\mathtt {Z}_n$ ($n\ge 0$), and $\overline{\mathtt {L}}=\mathtt {L}_1,...,\mathtt {L}_n$ be SPLs. If $\mathtt {Z}\preceq \mathtt {L}$ and $\mathtt {Z}_i\preceq \mathtt {L}_i$ ($1\le i\le n)$, then $\mathtt {Z}\preceq \mathtt {L}(\overline{\mathtt {L}})$.

In the following, we show that composition can also be done between DPLs: we just need to define the interface relation on DPLs and then extend the DPL-SPLs composition to DPL-DPL as well.

Definition 11

(DPL interface). An SPLS $\mathtt {Z}_{\textit{Int}}$ is an interface of an DPL $\mathtt {L}$ with dependencies $\overline{\mathtt {Z}}$, denoted as $\mathtt {Z}_{\textit{Int}}\preceq \mathtt {L}$, iff (i) $\mathcal {M}_{\mathtt {Z}_{\textit{Int}}}\preceq \mathcal {M}_{\mathtt {L}}$; and (ii) the generators $\mathcal {G}_{\mathtt {Z}_{\textit{Int}}}$, $\mathcal {G}_{\mathtt {L}}$ and $\mathcal {G}_{\overline{\mathtt {Z}}}$ are total and for each $p\in \mathcal {P}_{\mathtt {L}}$, $\mathcal {G}_{\mathtt {Z}_{\textit{Int}}}(p\cap \mathcal {F}_{\mathtt {Z}_{\textit{Int}}})\preceq \bigcup \mathcal {G}_{\mathtt {Z}}^\star (p\cap \mathcal {F}_{\mathtt {Z}})\cup \mathcal {G}_{\mathtt {L}}(p)$, where $\mathcal {G}_{\mathtt {Z}}^\star (p\cap \mathcal {F}_{\mathtt {Z}})$ is equal to $\mathcal {G}_{\mathtt {Z}}(p\cap \mathcal {F}_{\mathtt {Z}})$ with all method declarations extended with the body {return null;}.

The following definition extends the concept of DPL-SPLs composition (Definition 10) by accepting DPLs as arguments and yielding a DPL as result.

Definition 12

(DPL-DPLs composition). Let $\mathtt {L}$ be a DPL with dependencies $\overline{\mathtt {Z}}=\mathtt {Z}_1,...,\mathtt {Z}_n$ ($n\ge 0$) and $\overline{\mathtt {L}}=\mathtt {L}_1,...,\mathtt {L}_n$ be DPLs such that $\mathtt {Z}_i\preceq \mathtt {L}_i$ ($1\le i\le n)$. Let $\overline{\mathtt {Z}}^{(i)}=\mathtt {Z}_{i,1},...,\mathtt {Z}_{i,n_i}$ ($n_i\ge 0$) be the dependencies of $\mathtt {L}_i$ ($1\le i\le n$). The composition of $\mathtt {L}$ with $\overline{\mathtt {L}}$ is the DPL $\mathtt {L}_{0}=\mathtt {L}(\overline{\mathtt {L}})$, with dependencies $\overline{\mathtt {Z}}^{(1)},...,\overline{\mathtt {Z}}^{(n)}$, such that $\mathcal {M}_{ Main _{\mathtt {L}_{0}}}$, $\mathcal {K}_{\mathtt {L}_{0}}$ and $\textit{AB}_{\mathtt {L}_{0}}$ are defined as in Definition 10, and $\mathcal {M}_{ Glue _{\mathtt {L}_{0}}}$ is defined by $\mathcal {M}_{ Glue _{\mathtt {L}_{0}}}=\mathcal {M}_{ Glue _{\mathtt {L}_1}}\bullet \cdots \bullet \mathcal {M}_{ Glue _{\mathtt {L}_n}}$.

Note that, if the DPLs $\mathtt {L}_i$ ($1\le i\le n$) have no dependencies (i.e., $\overline{\mathtt {Z}}^{(i)}=\emptyset$ and $\mathcal {M}_{ Glue _{\mathtt {L}_{i}}}=\mathcal {M}_{ Id }$), then $\mathcal {M}_{ Glue _{\mathtt {L}_{0}}}=\mathcal {M}_{ Id }$ (like in Definition 10). Thus Definition 12 conservatively extends Definition 10. Moreover, Theorem 1 also holds when $\overline{\mathtt {L}}$ and $\mathtt {L}_{0}=\mathtt {L}(\overline{\mathtt {L}})$ are DPLs, and Theorem 2 can be extended as follows:

Theorem 3

(DPL-DPLs composition preserves interfacing). Let $\mathtt {Z}$ be an SPLS, $\mathtt {L}$ be a DPL with dependencies $\overline{\mathtt {Z}}=\mathtt {Z}_1,...,\mathtt {Z}_n$ ($n\ge 0$), and $\overline{\mathtt {L}}=\mathtt {L}_1,...,\mathtt {L}_n$ be DPLs. If $\mathtt {Z}\preceq \mathtt {L}$ and $\mathtt {Z}_i\preceq \mathtt {L}_i$ ($1\le i\le n)$, then $\mathtt {Z}\preceq \mathtt {L}(\overline{\mathtt {L}})$.

4 Compositionality of Existing SPL Analyses

In this section, we give two initial results illustrating the fact that our MPL model is well-suited for compositional analysis. First, we show that the results about the compositionality of existing analyses of feature models (void feature model, core features, dead features, void partial configuration, and atomic sets) given in [24, Sect. 5] can be used as-is in our model. Second, we show how to extend existing type systems for SPLs to ensure well-typedness in our model.

Compositional Analysis of Feature Models. The following theorem shows that the construction of the feature model of a DPL can be expressed as a sequence of $\circ$ operations. This, plus the fact that an SPLS $\mathtt {Z}$ is an interface of a DPL $\mathtt {L}$ only when $\mathcal {M}_\mathtt {Z}\preceq \mathcal {M}_\mathtt {L}$ ensures that the results presented in [24, Sect. 5] can be used as-is to analyse the feature models constructed in DPL-DPL compositions by analysing each feature model independently.

Theorem 4

Let $\mathcal {M}_x=(\mathcal {F}_x, \mathcal {P}_x)$, $\mathcal {M}_{y_1}=(\mathcal {F}_{y_1}, \mathcal {P}_{y_1})$,...,$\mathcal {M}_{y_n}=(\mathcal {F}_{y_n}, \mathcal {P}_{y_n})$, with $n\ge 1$, be feature models with pairwise feature disjointness (cf. Remark 2) and $\mathcal {M}_{\overline{y}} = \mathcal {R}(\mathcal {M}_{y_1}) \bullet \cdots \bullet \mathcal {R}(\mathcal {M}_{y_n})$. Then (for every permutation $w_1,...,w_n$ of $y_1,...,y_n$): $\mathcal {M}_{x/\overline{y}} = \mathcal {M}_x \circ _{\mathcal {M}_{ Glue }} \mathcal {M}_{\overline{y}} = ((\mathcal {M}_{x} \circ _{\mathcal {M}_{ Id }} \mathcal {M}_{w_1})\cdot \cdot \cdot \circ _{\mathcal {M}_{ Id }} \mathcal {M}_{w_{n-1}})\circ _{\mathcal {M}_{ Glue }} \mathcal {M}_{w_n}$.

Compositional Type System for MPLs. Type checking an SPL means to check that all its variants can be generated and are well-typed programs. Performing this check by generating each variant and type checking it does not scale (a product line with n features can have up to $2^n$ products). Therefore, several SPL type checking approaches have been proposed in the literature [27]. Three type checking approaches for delta-oriented SPLs have been proposed and formalized [5, 8, 9] by means of the IF$\varDelta$J calculus.

In our MPL model, we add two structures that can be type-checked: DPLs and DPL-DPL compositions. However, due to the fact that the artifact base of a DPL depends on code defined in other DPLs, it is too restrictive to require that its variants are well-typed programs: they can indeed contain missing dependencies. The following definition extends the notion of well-typedness to DPL to deal with the missing dependency problem:

Definition 13

(Well-typed DPL). The stub-completion of an SPLS $\mathtt {Z}$, written $\mathtt {Z}^\star$, is the SPL obtained by adding the body {return null;} to all the method declarations in $\mathtt {Z}$. The stub-completion of a DPL $\mathtt {L}$ with dependencies $\overline{\mathtt {Z}}=\mathtt {Z}_1,...,\mathtt {Z}_n$ ($n\ge 0$) is the SPL $\mathtt {L}^\star =\mathtt {L}(\mathtt {Z}_1^\star ,...,\mathtt {Z}_n^\star )$ obtained by composing $\mathtt {L}$ with the stub-completion of its dependencies. We say that a DPL is well-typed iff its stub-completion is well-typed.

Note that this definition generalizes the notion of well-typedness for SPLs: when the set of dependencies of the DPL $\mathtt {L}$ is empty ($n=0$), $\mathtt {L}$ is well-typed iff it is well-typed in the SPL-sense of the term. Moreover, with this definition, extending the exisiting type-checking algorithms for SPL to manage DPL simply requires a pre-processing of the DPL to transform it in an SPL as described in the definition. An additional important property of this definition is that it is enough to type-check in isolation the DPLs in a DPL-DPL composition to ensure that the resulting DPL is well-typed:

Theorem 5

(Compositionality of DPL-DPLs composition type checking). Let $\mathtt {L}$ be a DPL with dependencies $\overline{\mathtt {Z}}=\mathtt {Z}_1,...,\mathtt {Z}_n$ ($n\ge 0$) and $\overline{\mathtt {L}}=\mathtt {L}_1,...,\mathtt {L}_n$ be DPLs such that $\mathtt {Z}_i\preceq \mathtt {L}_i$ ($1\le i\le n)$. If each of the DPLs $\mathtt {L},\mathtt {L}_1,...,\mathtt {L}_n$ type checks, then $\mathtt {L}(\mathtt {L}_1,...,\mathtt {L}_n)$ type checks.

Note that the SPLs CapitalAccount and FinancialAccount (in Fig. 3), and the DPL DualAccount (in Fig. 6) type check: we can then conclude that the SPL DualAccount(CapAccount,FinAccount) type checks as well.

Checking the Interface Relation. The compositional analysis of feature models and the well-typedness of a DPL-DPL composition $\mathtt {L}(\overline{\mathtt {L}})$ presented previously heavily rely on the interface relation being satisfied between the dependencies of $\mathtt {L}$ and the DPLs $\overline{\mathtt {L}}$. It is possible to automatically check this relation between any SPLS $\mathtt {Z}$ and any DPL $\mathtt {L}$ using a predicate formula written ${\texttt {match}}(\mathtt {Z},\mathtt {L})$. Due to lack of space, we cannot give the definition of this formula, we simply state the following theorem:

Theorem 6

(DPL interface checking). If the SPLS $\mathtt {Z}$ and DPL$\mathtt {L}$ type check and $\mathcal {M}_{\mathtt {Z}}\preceq \mathcal {M}_{\mathtt {L}}$ holds, then ${\texttt {match}}(\mathtt {Z},\mathtt {L})$ is valid if and only if $\mathtt {Z}\preceq \mathtt {L}$ holds.

5 Related Work and Conclusions

An extension of DOP to implement MPLs has been outlined in [10] by proposing linguistic constructs for defining an MPL as an SPL that imports other SPLs. The feature model and the artifact base of the importing SPL is deeply integrated with the feature models and the artifact bases of the imported SPLs, respectively. This extension is very flexible, but it does not enforce any boundary between different SPLs—thus providing no support for compositional analyses.

Schröter et al. [25] advocated investigating suitable interfaces in order to support compositional analyses of MPLs for different stages of the development process. In particular, syntactical interfaces, which build on feature model interfaces to provide a view of reusable programming artifacts, and behavioral interfaces, which in turn build on syntactical interfaces to support formal verification. More recently, Schröter et al. [24] proposed a concept of feature model interface that consists of a subset of features (thus it hides all other features and dependencies) and used it in combination with a concept of feature model composition through aggregation to support compositional analyses of feature models—see Sect. 2.2. In this paper we build on [24] and propose the concepts of SPLS, DPL, and DPL-DPLs composition and show how to use them to support compositional type checking of delta-oriented MPL. An SPL signature is a syntactical interface that provides a variability-aware API, expressed in the flexible and modular DOP approach, specifying which classes and members of the variants of a DPL are intended to be accessible by variants of other DPLs.

Feature-context interfaces [26] are aimed at supporting type checking SPLs developed according to the FOP approach which, as pointed out in Sect. 1, is encompassed by DOP (see [22] for a detailed comparison between FOP and DOP). A feature-context interface supports type checking a feature module in the context of a set of features FC. It provides an invariable API specifying classes and members of the feature modules corresponding to the features in FC that are intended to be accessible. In contrast, our concept of SPLS represents a variability-aware API that supports compositional type checking of MPLs. Notably, since DOP is an extension of FOP, our results apply also to FOP SPLs.

Kästner et al. [16] proposed a variability-aware module system, where each module represents an SPL, that allows for type checking modules in isolation. Variability inside each module and its interface is expressed by means of #ifdef preprocessor directives and variable linking, respectively. In contrast to our SPLSs, module interfaces do not support hiding features and dependencies. A major difference with respect to our proposal is in the approach used to implement variability (i.e., to build variants): [16] considers an annotative approach (#ifdef preprocessor directives), while we consider a transformational approach (DOP)—we refer to [23, 27] for classification and survey of different approaches for implementing variability.

Schröter et al. [24] defined a slice function for feature models (similar to the operator proposed by Acher et al. [1]) that generates a feature-model interface by removing a given set of features. In future work we would like to generalize the slice function for feature models to DPLs, thus providing an automatic means for generating an interface for a given DPL.

Recently, Thüm et al. [28] proposed a notion of behavioral interface for supporting compositional verification of FOP SPLs via variability encoding [29]. In future work we would like to enrich SPLSs with method contracts (thus promoting them to behavioral interfaces) in order to support compositional verification of delta-oriented DPLs by building on recently proposed proof systems and techniques for the verification of delta-oriented SPLs [6, 11, 12].

We plan to implement our approach for both DeltaJ 1.5 [17] (a prototypical implementation of DOP that supports full Java 1.5) and the Abstract Behavioral Specification modeling language [15].