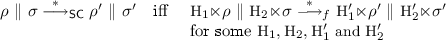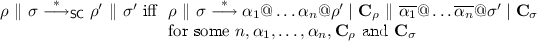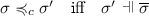Abstract
Behavioral contracts are abstract descriptions of the communications that clients and servers perform. Behavioral contracts come naturally equipped with a notion of compliance: when a client and a server follow compliant contracts, their interaction is guaranteed to progress or successfully complete. We study two extensions of contracts, dealing respectively with backtracking and with speculative execution. We show that the two extensions give rise to the same notion of compliance. As a consequence, they also give rise to the same subcontract relation, which determines when one server can be replaced by another preserving compliance. Moreover, compliance and subcontract relation are both decidable in polynomial time.
This work was partially supported by the COST Action IC1405 on “Reversible computation - extending horizons of computing”. The first and third authors were partially supported also by the COST Action EUTYPES CA-15123 and, respectively, Project FIR 1B8C1 of the University of Catania and Project FORMS 2015 of Turin. We thank Mariangiola Dezani-Ciancaglini for interesting discussions and useful suggestions.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Operational Semantic
- Label Transition System
- Conservative Extension
- Speculative Execution
- Speculative Contract
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Binary behavioral contracts [14, 15, 27] and binary session types [22] are abstractions of programs used to statically ensure that a client and a server interact successfully (see the survey in [24]). Along the years, the basic theory has been extended to deal with many features of clients and servers, such as exceptions [12], time [9], and so on. We consider here two new features: backtracking, allowing one to go back to previous stages of the interaction, and speculative execution [30], allowing one to try different alternatives concurrently. These two features have quite different origin and aims. Backtracking is used to avoid failures due to wrong past decisions in a wide range of settings, from the undo button in web browsers, to the execution model of Prolog, to techniques for rollback-recovery [1]. Speculative execution is used for efficiency reasons in different areas, from simulation [13], to thread-level optimization [31], to web services [16].
We present two extensions of binary contracts (Sect. 2): retractable contracts capturing backtracking, and speculative contracts capturing speculative execution. The two extensions are based on the same syntax, but naturally have different semantics. Essentially, they add to the session contracts of [3, 10] (called first-order session behaviors in [3]) an operator of external choice among output operations. The most interesting case is when an external choice among outputs and an external choice among inputs interact. In the retractable semantics, the client and the server agree on which option to explore, but they rollback and try a different possibility if the computation gets stuck. In the speculative semantics all the possibilities are explored concurrently, and it is enough for one of them to succeed to guarantee the success of the whole computation.
This paper defines retractable and speculative contracts, and studies the related theory, considering the notions of compliance (Sect. 3), guaranteeing that the interaction progresses or successfully completes, subcontract relation (Sect. 4), determining when a server (resp. client) can be replaced by another server (resp. client) preserving compliance, and dual contract (Sect. 4), that is the most general contract (in terms of the subcontract relation) compliant with a given contract. Our analysis provides two main insights:
-
Even if retractable contracts and speculative contracts have different semantics and give rise to different client-server interactions, the relations of compliance, subcontract and duality in the two settings do coincide. While surprising at first sight, this can be explained by noticing that in both the cases different alternatives are explored (sequentially for retractable contracts, in parallel for speculative contracts) and the success of one of them guarantees the success of the whole computation. In other terms, the two semantics provide different implementations of angelic nondeterminism, first described by Hoare [21].
-
While retractable/speculative contracts are strictly more expressive than session contracts (indeed they are a conservative extension, see Sect. 3.1), their theory preserves the main good properties of the theory of session contracts. In particular, compliance and subcontract relations are both decidable (Sect. 3) in polynomial time (Sect. 5), and the dual of a contract always exists and has a simple syntactic characterization (Sect. 4).
A natural way to ensure the existence of the dual contract is to introduce an operator of internal choice among inputs. While this operator has limited practical impact, it makes the model more symmetric and the mathematical treatment simpler.
A few preliminary results on the topic of this paper have been presented in a workshop paper [7], which considers retractable session contracts, i.e., retractable contracts without internal choice among inputs. The main result of [7] is the decidability of the compliance relation (while we study here also the complexity), which was obtained via an algorithm that we now know to be exponential. Here we present a more refined, polynomial one (Fig. 7). In [7] the subcontract relation and the dual contract were not studied, and indeed the dual contract did not exist due to the absence of internal choice among inputs.
Proofs, additional examples and additional background material are available in a companion technical report [8].
2 Contracts for Retractable and Speculative Interactions
We present below a uniform syntax for retractable and speculative contracts, with two semantics. It can be obtained from the syntax of session contracts of [3, 10] (called first-order session behaviors in [3]), that we dub here \(\mathsf {SC}\), just adding external retractable/speculative choice among outputs and internal choice among inputs. As a matter of fact our contracts can also be seen as an extension of the retractable session contracts of [7], that we dub here \(\mathbf {r}\mathsf {C}\), simply adding internal choice among inputs. Basics of session contracts and retractable session contracts are recalled in the companion technical report [8].
Definition 1
(Retractable/Speculative Contracts). Let \(\mathcal{N}\) (set of names) be some countable set of symbols and let \(\overline{\mathcal{N}}\) (set of conames) be \(\{\overline{a} \mid a \in \mathcal{N}\}\), with \(\mathcal{N}\cap \overline{\mathcal{N}}= \emptyset \). The set \(\mathbf {rs}\mathsf {C}\) of retractable/speculative contracts is defined as the set of the closed expressions generated by the following grammar,
where I is non-empty and finite, the names and the conames in choices are pairwise distinct and \(\sigma \) is not a variable in \(\mathsf{rec} \, x.\sigma \).
Recursion in \(\mathbf {rs}\mathsf {C}\) is guarded and hence contractive in the usual sense. We take an equi-recursive view of recursion by equating \(\mathsf{rec} \, x.\sigma \) with \(\sigma [\mathsf{rec} \, x.\sigma /x]\). We use \(\alpha \) to range over \(\mathcal{N}\cup \overline{\mathcal{N}}\), with the convention \(\overline{\alpha }= \overline{a}\) if \(\alpha =a\), and \(\overline{\alpha }=a \) if \(\alpha =\overline{a}\). We write \(\alpha _1.\sigma _1 + \alpha _2.\sigma _2\) for binary external input/output choice and \(\alpha _1.\sigma _1 \oplus \alpha _2.\sigma _2\) for binary internal input/output choice. They are both commutative by definition. Also, \(\alpha .\sigma \) denotes both internal and external unary choice. This is not a source of confusion since internal and external choices do coincide in the unary case. We also write \(\alpha _k.\sigma _k + \sigma '\) for \(\sum _{i\in I} \alpha _i.\sigma _i\) where \(k\in I\) and \(\sigma '=\sum _{i\in (I\setminus \{k\})} \alpha _i.\sigma _i\) (and similarly for internal choices). When no ambiguity can arise, we call just contracts the expressions in \(\mathbf {rs}\mathsf {C}\). They are written by omitting all trailing \(\mathbf{1}\)’s.
We discuss below the two interpretations and the two semantics for our contracts: the retractable one, and the speculative one.
2.1 Retractable Semantics
The main novelty of the retractable semantics is that when an external choice among outputs and an external choice among inputs interact, the client and the server agree on which option to explore, but they rollback and try a different possibility if the computation gets stuck.
In order to deal with rollbacks, we decorate contracts with their history, which memorizes, for past choices, the alternatives that have been discharged and that can be tried upon rollback. We use ‘\(\circ \)’ to stand for no-remaining-alternatives.
Definition 2
(Contracts with History). Let \(\mathsf{Histories}\) be the expressions generated by the grammar \(\small {\textsc {H}}\,{:}{:=}\, \langle \;\rangle \mid \small {\textsc {H}}\!:\!\sigma \), where \(\sigma \in \mathbf {rs}\mathsf {C}\cup \{\circ \}\) and \(\circ \not \in \mathbf {rs}\mathsf {C}\). \(\mathsf{Histories}\) are hence stacks of contracts and \(\circ \). Then the set of contracts with history is defined by: \(\mathbf {rs}\mathsf {C}\mathsf{H}= \{ \small {\textsc {H}}{\ltimes }\sigma \mid \small {\textsc {H}}\in \mathsf{Histories}, \sigma \in \mathbf {rs}\mathsf {C}\cup \{\circ \}\, \}.\)
We write just \(\sigma _1\!:\!\cdots \!:\!\sigma _k\) for the stack \((\cdots (\langle \;\rangle \!:\!\sigma _1) \!:\!\cdots )\!:\!\sigma _{k}\).
As standard for contracts, the definition of the retractable semantics is in two stages: we first define a labeled transition system (LTS) for contracts with history (Definition 3), and then we use it to define a reduction semantics for pairs of contracts representing one client and one server (Definition 4).
Definition 3
(Semantics of Contracts with History).
In the transition rule for external choice (\(+\)), the action \(\alpha \) is executed, and the discharged branches in \(\sigma '\) are memorized. In internal choice (\(\oplus \)), instead, the selection of one branch is represented by a label \(\tau \), and the history \(\small {\textsc {H}}\) is unchanged. When a single action is executed \((\alpha )\), a ‘\(\circ \)’ is added to the history, meaning that the only possible branch has been tried and no alternative is left. Rule \(({\textsf {rb}})\) pops the contract at the top of the stack, replacing the current one with it.
The client/server interaction is modeled by the reduction of their parallel composition, that can be either forward, consisting of CCS-style synchronizations and single internal choices, or backward, only when there is no possible forward reduction, and the client is not satisfied, i.e., it is different from \(\mathbf{1}\).
Definition 4
(Semantics of Retractable Client/Server Pairs).
The following rules, plus the rule symmetric to \((\tau )\) w.r.t. \(\Vert \), define the relation  over pairs of contracts with history:
over pairs of contracts with history:

Rule \((\mathsf {rbk})\) applies only if neither \((\mathsf {comm})\) nor \((\tau )\) do.
The forward reduction  is the relation generated by rules (\(\tau \)) and (\(\textsf {comm}\)).
is the relation generated by rules (\(\tau \)) and (\(\textsf {comm}\)).
Remark 1
The semantics defined above for retractable client/server pairs can be seen as an instantiation on contracts of the standard reversible semantics for process calculi, see, e.g., [17, 25, 26, 29]. In particular, the semantics would become a classic uncontrolled semantics (according to the terminology in [26]) by removing the four control mechanisms below:
-
1.
the fact that only external choices are retractable;
-
2.
the side condition \(\rho \ne \mathbf{1}\) in rule \(({{{\textsf {\textit{rbk}}}}})\), which disallows backtrack after success;
-
3.
the fact that rule \(({{{\textsf {\textit{rbk}}}}})\) can be applied only if no other rule applies, ensuring that backtrack is enabled only when no forward reduction is possible;
-
4.
the fact that in external choices the selected path is not stored in the history, so that each path can be tried at most once.
These mechanisms provide a semantic control of reversibility [26], specifying which rollback steps are allowed, and when. We discuss in Remark 2 the impact that removing the above control mechanisms would have on retractable contracts and on their theory.
Example 1
Retractable contracts allow one to first try a preferred alternative, but to accept also another alternative if the first one proves to be impossible to obtain. In cloud computing settings, companies may hire virtual machines and storing facilities from cloud providers with some agreed Quality of Service (QoS). A company is willing to hire at some medium or low price a certain amount of machines for online elaboration during day time, but, if the price is too high, it is also willing to switch to offline night elaboration. In this last case it is only willing to pay a low price.
A retractable contract with this behavior may be written as:
Notice that the contract does not specify which alternative the client prefers: this aspect of the client behavior is abstracted away. A sample server is:

A sample interaction is described in Fig. 1, where we assume that
2.2 Speculative Semantics
The main idea of the speculative semantics is that in an external output choice all the options are tried concurrently: if at least one of them succeeds, then the whole computation succeeds. In order to represent concurrent trials we need runtime contracts featuring multiple threads.
Definition 5
(Contracts with Threads). Contracts with threads \(\mathbf {C}\), used as runtime syntax for contracts, are parallel compositions of threads \(\mathbf {T}\). Each thread is a contract prefixed by a sequence (possibly empty) of actions uniquely identifying it.
We assume the operator ‘ \(\mid \)’ to be associative and commutative.
As for the retractable semantics, the definition of the speculative semantics is in two stages: we first define an LTS for contracts with threads (Definition 6), and then we use it to define a reduction semantics for pairs of contracts with threads representing one client and one server (Definition 7).
Definition 6
(Semantics of Contracts with Threads).
In the LTS below, we use as labels actions \(\alpha \,{:}{:=}\, a \mid \overline{a}\), sequences of actions \(\beta \,{:}{:=}\, \alpha \mid \alpha \beta \), and complex labels \(\beta _{\tau } \,{:}{:=}\, \tau \mid \beta \mid \beta , \mathbf {T}\).

In the rule for external choice (Fork), when an action \(\alpha \) is executed, its continuation \(\sigma \) is prefixed by it. The other branches \(\sigma '\) need to be executed in a freshly spawned thread. Since such thread needs to be installed at top level, \(\sigma '\) is added to the label, and the actual installation is performed at the level of speculative client/server pairs (see rule (comm) in Definition 7). The rule for internal choice \((\oplus )\) simply selects one of the available options. A unary choice \((\alpha )\) executes the action \(\alpha \) and prefixes with it the continuation \(\sigma \).
Because of rules \((@\text{- }\alpha )\), \((@\text{- }\alpha \text{- }T)\), and \((@\text{- }\tau )\), execution is allowed below an @ prefix. In rule \((@\text{- }\alpha )\), the prefix itself is added to the label \(\beta \). Prefixes uniquely identify threads, and ensure that each thread interacts only with the one with dual prefix which is running on the communication partner. This is specified in Definition 7 below. Rule \((@\text{- }\alpha \text{- }T)\) is analogous to rule \((@\text{- }\alpha )\), but the label also contains a thread \(\mathbf {T}''\), and the prefix \(\alpha \) is added to both \(\beta \) and \(\mathbf {T}''\). No prefix is added to \(\tau \) actions, propagated by rule \((@\text{- }\tau )\). Rule (ParL) simply allows components of a parallel composition to execute (a symmetric rule is not needed thanks to the commutativity of \(\mid \)).
The interaction of a client with a server is modeled by the reduction of their parallel composition.
Definition 7
(Semantics of Speculative Client/Server Pairs).
The following rules, plus the rule symmetric to \((\tau )\) w.r.t. \(\Vert \), define the relation  over pairs of contracts with threads. In the LTS below, \(? \mathbf {T}\) denotes either the thread \(\mathbf {T}\) or nothing. Hence, \(\beta , ? \mathbf {T}\) and \(\mathbf {C}\mid ? \mathbf {T}\) are respectively \(\beta \) and \(\mathbf {C}\) if \(? \mathbf {T}\) is nothing, and \(\beta , \mathbf {T}\) and \(\mathbf {C}\mid \mathbf {T}\) otherwise. Also, the duality operator extends from actions to sequences: \(\overline{\alpha \beta }=\overline{\alpha }\overline{\beta }\).
over pairs of contracts with threads. In the LTS below, \(? \mathbf {T}\) denotes either the thread \(\mathbf {T}\) or nothing. Hence, \(\beta , ? \mathbf {T}\) and \(\mathbf {C}\mid ? \mathbf {T}\) are respectively \(\beta \) and \(\mathbf {C}\) if \(? \mathbf {T}\) is nothing, and \(\beta , \mathbf {T}\) and \(\mathbf {C}\mid \mathbf {T}\) otherwise. Also, the duality operator extends from actions to sequences: \(\overline{\alpha \beta }=\overline{\alpha }\overline{\beta }\).

Rule (comm) allows threads performing dual sequences of actions to interact. This implies that both the actual actions and the prefixes of the threads performing them should be dual. Threads in the labels, if present, are installed in parallel. Rule \((\tau )\) simply propagates the \(\tau \) action.
Example 2
A server provides access to multiple algorithms for SAT solving [35]. A client first sends the problem instance to be solved, then selects the algorithm, and finally sends the relevant parameters. The server computes the solution according to the received commands, and sends it back. Since the most efficient technique depends on the problem instance [34], the server supports speculative execution, to allow one to try different algorithms at the same time (this is called the portfolio approach). The server contract is described by:
A simple client that tries both the DPLL approach and the walksat approach can be modeled as follows:
A sample computation proceeds as described in Fig. 2, assuming that the server supports both DPLL and walksat. To keep the example simple we drop the choice of parameters. Let us see in more details how the creation of threads is managed. The first reduction in Fig. 2 is due to rule (comm), since
and
The second reduction is also due to rule (comm), since, on the client side

whereas, on the server side,

3 Compliance
The compliance relation for session contracts [3, 10] consists in requiring that, whenever no reduction is possible, all client’s requests and offers have been satisfied, i.e. the client is in the success state \(\mathbf{1}\). For retractable contracts, thanks to the retractable operational semantics taking care of forward and backward reductions, we can adopt the same definition. We use \(\mathop {\longrightarrow }\limits ^{*}\) to denote the reflexive and transitive closure of  , and
, and  to specify that no
to specify that no  reduction exists.
reduction exists.
Definition 8
(Retractable Compliance Relation
 ).
).
-
(i)
The relation
 on contracts with history is defined by:
on contracts with history is defined by: 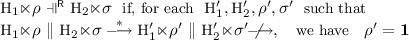
-
(ii)
The relation
 on contracts is defined by:
on contracts is defined by: 
For speculative contracts we need to take into account the fact that the whole computation succeeds if at least one of its branches succeeds.
Definition 9
(Speculative Compliance Relation
 ).
).
The relation  on contracts is defined by:
on contracts is defined by:

We now provide a formal system characterizing compliance on both retractable and speculative contracts.
Definition 10
(Formal System for Compliance \(\vartriangleright \) ).
Judgments in the formal system \({\vartriangleright }\) are expressions of the form  , where the environment \(\varGamma \) is a finite set of expressions of the form
, where the environment \(\varGamma \) is a finite set of expressions of the form  , with \(\rho ,\sigma ,\delta ,\gamma \in \mathbf {rs}\mathsf {C}\). Axioms and rules are as in Fig. 3.
, with \(\rho ,\sigma ,\delta ,\gamma \in \mathbf {rs}\mathsf {C}\). Axioms and rules are as in Fig. 3.
The only non standard rule of system \(\vartriangleright \) is \((+\cdot +)\), which ensures compliance of two external choices when they contain respectively (at least) one \(\alpha \) and the corresponding \(\overline{\alpha }\), followed by compliant contracts. This contrasts with the rules \((\oplus \cdot +)\) and \((+\cdot \oplus )\), where each \(\alpha \) in an internal choice must have a corresponding \(\overline{\alpha }\) in the external choice, followed by compliant contracts. No rule is provided for the case \((\oplus \cdot \oplus )\) since two internal choices are compliant only if both of them are unary choices (otherwise they may always get stuck by choosing incompatible actions). Since unary internal choice coincides with unary external choice, this case is taken into account by the rules we already have. Notice that rule \((+\cdot +)\) implicitly represents the fact that, in the decision procedure for two contracts made of external choices, the possible synchronizing branches have to be tried, until either a successful one is found or all fail. Looking at a derivation bottom-up, at each application of a rule, the considered pair of contracts is added to the environment \(\varGamma \). In this way, if the same pair is reached again due to the equi-recursive view of contracts, the derivation can be closed using rule \(({\textsc {Hyp}})\). Rule \(({{\textsc {Ax}}})\) instead closes the derivation when the client reaches the success state \(\mathbf{1}\). We write  instead of
instead of  when \(\varGamma \) is empty.
when \(\varGamma \) is empty.
Derivability in system \(\vartriangleright \) is decidable, since it is syntax-directed and proof reconstruction does terminate.
Theorem 1
Derivability in the formal system \(\vartriangleright \) is decidable.
We can prove the soundness and the completeness of the formal system \(\vartriangleright \) w.r.t. both the retractable and the speculative semantics (see [8] for the proofs).
Theorem 2
(Retractable Soundness and Completeness).

Theorem 3
(Speculative Soundness and Completeness).

By the soundness and completeness of system \(\vartriangleright \) w.r.t. both the relations of retractable and speculative compliance, we immediately get that the two compliance relations do coincide.
Corollary 1
(Retractable and Speculative Compliances Coincide).

By the above, from now on we write  instead of
instead of  or
or  . So the following also easily follows.
. So the following also easily follows.
Corollary 2
(Compliance Decidability). The relation  is decidable.
is decidable.
Remark 2
We now discuss the impact on the compliance relation of the four mechanisms for controlling reversibility in the semantics of retractable client/server pairs (see Remark 1). In particular, we analyze what would happen by dropping each one of them in isolation:
- Drop “Not all reductions are retractable”::
-
each reduction could be undone. From the compliance point of view, all the choices would be retractable. Hence, retractable contracts would not be a conservative extension (see Subsect. 3.1) of session contracts any more. The case we consider is strictly more general, since we allow for both retractable and unretractable choices.
- Drop the side condition \(\rho \ne \mathbf{1}\) in rule \(({{\mathbf {\mathsf{{rbk}}}}})\) of Definition 4::
-
any forward finite interaction would be followed by a rollback. In particular, most of the client/server pairs without recursion (except a few trivial ones, like \(\langle \;\rangle {\ltimes }\mathbf{1}~\Vert ~\langle \;\rangle {\ltimes }\sigma \)) would end into \(\langle \;\rangle {\ltimes }\circ ~\Vert ~\langle \;\rangle {\ltimes }\circ \). Thus all these pairs of contracts would not be compliant.
- Drop “rule \(({{\mathbf {\mathsf{{rbk}}}}})\) can be applied only if no other rule applies”::
-
interactions could rollback before succeeding. As in the case above, most client/server pairs (except a few trivial ones, but including recursive ones) could reduce to \(\langle \;\rangle {\ltimes }\circ ~\Vert ~\langle \;\rangle {\ltimes }\circ \). Again all these pairs of contracts would not be compliant.
- Drop “in choices the chosen path is not memorized”::
-
any client/server pair that would not normally succeed with at least one retractable choice could diverge by undoing and redoing the choice forever, thus trivially ensuring compliance.
None of the last three scenarios provides a reasonable setting. The first one would be reasonable, but the case we consider is strictly more general.
3.1 Conservativity Results
It is possible to show that all the relations on our retractable and speculative contracts (\(\mathbf {rs}\mathsf {C}\)) are conservative extensions of corresponding notions on (first-order) session contracts (\(\mathsf {SC}\)) as defined in [3, 10], and on the retractable session contracts (\(\mathbf {r}\mathsf {C}\)) as defined in [7].
As previously said, it is not difficult to check that session contracts \(\mathsf {SC}\) are a subset of retractable session contracts \(\mathbf {r}\mathsf {C}\), which, in turn, are a subset of the contracts \(\mathbf {rs}\mathsf {C}\) we are presently investigating, namely: \(\mathsf {SC}\subsetneq \mathbf {r}\mathsf {C}\subsetneq \mathbf {rs}\mathsf {C}.\) Obviously the strict inclusion \(\mathsf {SC}\subsetneq \mathbf {rs}\mathsf {C}\) is not enough, by itself, to guarantee the retractable and speculative operational semantics for \(\mathbf {rs}\mathsf {C}\) to be conservative extensions of the operational semantics of \(\mathsf {SC}\). We prove that it is so in the following Proposition 1. Informally, it states that both the forward retractable semantics  and the speculative semantics
and the speculative semantics  of pairs of contracts in \(\mathsf {SC}\) are annotated versions of their semantics in \(\mathsf {SC}\)(recalled in the companion technical report [8]).
of pairs of contracts in \(\mathsf {SC}\) are annotated versions of their semantics in \(\mathsf {SC}\)(recalled in the companion technical report [8]).
Proposition 1
(Operational Semantics Conservativity). Let \(\rho ,\sigma \in \mathsf {SC}\).
-
(i)
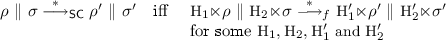
-
(ii)
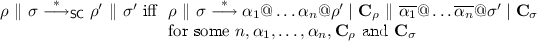
where  denotes the reduction relation on \(\mathsf {SC}\) pairs in the theory of session contracts.
denotes the reduction relation on \(\mathsf {SC}\) pairs in the theory of session contracts.
We do not take into account conservativity of the retractable operational semantics for \(\mathbf {rs}\mathsf {C}\) over the one for \(\mathbf {r}\mathsf {C}\) because it is quite trivial, since the rules in the two semantics are essentially the same. A conservativity result of the speculative operational semantics for \(\mathbf {rs}\mathsf {C}\) over the one for \(\mathbf {r}\mathsf {C}\) would instead consist in a rather cumbersome and uninteresting statement.
The conservativity result for the operational semantics is not enough, in itself, to guarantee the theory of retractable compliance for \(\mathbf {rs}\mathsf {C}\) to be a conservative extension of both the theory of compliance for \(\mathbf {r}\mathsf {C}\) and for \(\mathsf {SC}\). Also in this case, however, we can prove it to be so, that is, the compliance relation for session contracts \(\mathsf {SC}\) is the restriction of the compliance relation  for our contracts to pairs of session contracts \(\mathsf {SC}\), and similarly for the restriction of
for our contracts to pairs of session contracts \(\mathsf {SC}\), and similarly for the restriction of  to retractable session contracts \(\mathbf {r}\mathsf {C}\).
to retractable session contracts \(\mathbf {r}\mathsf {C}\).
Proposition 2
(Compliances Conservativity).
-
(i)
Let

-
(ii)
Let

4 Duality and the Subcontract Relation
Unlike the retractable session contracts of [7], in the present setting it is possible to get a natural notion of duality. The dual \(\overline{\sigma }\) of an element \(\sigma \) of \(\mathbf {rs}\mathsf {C}\) is obtained, as for session contracts, by interchanging any name a with \(\overline{a}\) and \(+\) with \(\oplus \).
The notion of dual contract allows one to combine pairs of contracts in the compliance relation, as follows:
Proposition 3
For any \(\rho ,\sigma ,\sigma '\in \mathbf {rs}\mathsf {C}\), 
We will provide further properties of duality using the notion of subcontract relation. Indeed, the notion of compliance naturally induces a substitutability relation on servers, denoted \(\preccurlyeq _s\), that we call subcontract relation for servers. Such a relation may be used for implementing contract-based query engines (see [28] for a detailed discussion). An analogous subcontract relation, denoted \(\preccurlyeq _c\), can be defined for clients.
Definition 11
(Subcontract Relations for Servers and for Clients). Let \(\sigma , \sigma ' \in \mathbf {rs}\mathsf {C}\). We define
-
(i)

-
(ii)

Using Proposition 3 we can characterize both \(\preccurlyeq _s\) and \(\preccurlyeq _c\) in terms of duality and compliance, relate them and get their decidability.
Theorem 4
For any \(\sigma , \sigma '\in \mathbf {rs}\mathsf {C}\):
-
(i)

-
(ii)
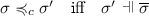
-
(iii)
\(\sigma \preccurlyeq _s\sigma ' ~~ \text{ iff } ~~ \overline{\sigma '} \preccurlyeq _c\overline{\sigma }\)
-
(iv)
\(\sigma \preccurlyeq _s\sigma '\) and \(\sigma \preccurlyeq _c\sigma '\) are decidable.
By item (iii) above, from now on we can simply concentrate on the relation \(\preccurlyeq _s\).
We can now characterize duality in terms of the subcontract relation for servers: given a client \(\rho \), its dual \(\overline{\rho }\) is a least element among all its possible servers, that is it is a possible server, and it is smaller than all the other possible servers.
Proposition 4
(Dual as a Least Element w.r.t. \(\preccurlyeq _s\) ).
Let \(\rho \in \mathbf {rs}\mathsf {C}\). Then \(\overline{\rho }\) is a server for \(\rho \), namely  , and more precisely it is a least element in the set of the servers of \(\rho \), that is,
, and more precisely it is a least element in the set of the servers of \(\rho \), that is,

Since we have not yet proved that the subcontract relation is a partial order, we do not know yet whether \(\overline{\rho }\) is also a minimal, i.e. there is no smaller element, neither whether other least elements or minimal elements exist. These questions will be answered by Proposition 5.
As done for the compliance relation, we characterize now the subcontract relation for servers in terms of derivability in the following formal system, where the symbol \(\ll \) is used as syntactical counterpart of the relation \(\preccurlyeq _s\).
Definition 12
(Formal System for Subcontract \(\blacktriangleright \) ). Judgments in the formal system \(\blacktriangleright \) are expressions of the form \(\varGamma \,{\blacktriangleright }\, \rho \ll \sigma \), where the environment \(\varGamma \) is a finite set of expressions of the form \(\delta \ll \gamma \), with \(\rho ,\sigma ,\delta ,\gamma \in \mathbf {rs}\mathsf {C}\). Axioms and rules are as in Fig. 4.
The rules in system \(\blacktriangleright \) can be read as a translation of the rules in system \(\vartriangleright \) via Theorem 4(i). As for \(\vartriangleright \), in \(\varGamma \,{\blacktriangleright }\, \rho \ll \sigma \) we may drop \(\varGamma \) if empty.
System \(\blacktriangleright \) is sound and complete for the subcontract relation \(\preccurlyeq _s\).
Theorem 5
(Soundness and Completeness of \(\blacktriangleright \) ). \({\blacktriangleright }\, \sigma {\ll }\sigma ' ~ \text{ iff } ~ \sigma {\preccurlyeq _s}\sigma '\)
System \(\blacktriangleright \) can be used to show that \(\preccurlyeq _s\) is a partial order and hence, by antisymmetry, \(\overline{\rho }\) is also the minimum server of \(\rho \): it is minimal, hence there is no smaller server, and there is a unique minimal.
Proposition 5
\(\preccurlyeq _s\) is a partial order \(\wedge \) \(\forall \rho {\in } \mathbf {rs}\mathsf {C}\), \(\overline{\rho }\) is the minimum server of \(\rho \).
The structure of the partial order is shown in Fig. 5, where the relations between terms with a unique choice among actions a, b, c, \(\overline{a}\), \(\overline{b}\) and \(\overline{c}\) are pictured.
Remark 3
Analogously to what done in Subsect. 3.1, one can show the subcontract relation \(\preccurlyeq _s\) to be a conservative extension of the corresponding notion in \(\mathsf {SC}\). Moreover, the restriction of \(\preccurlyeq _s\) to \(\mathbf {r}\mathsf {C}\) provides a suitable notion of subcontract for \(\mathbf {r}\mathsf {C}\) (which has never been studied before).
5 Complexity Issues
One can define a decision procedure for compliance as the recursive proof-search algorithm obtained by reading bottom-up the rules of the formal system for compliance in Fig. 3. A similar algorithm is described in [7]. We show below that such an algorithm is strictly exponential.
To show it, roughly, it is possible to adapt the example presented in [20](Sect. 11) concerning the subtyping relation for recursive arrow and product types.
For each \(n\in \mathbb {N}\) we define two contracts \(\rho _n\) and \(\sigma _n\) by induction, as follows.
As for the example in [20], the size of \(\rho _n\) and \(\sigma _n\) is linear in n, since \(\rho _n\) and \(\sigma _n\) appear just once in the definitions of \(\rho _{n+1}\) and \(\sigma _{n+1}\), respectively. By complete induction over n it is possible to prove that, for any n,  . By recursive breadth-first search, a derivation for
. By recursive breadth-first search, a derivation for  is built in an actual exponential number of calls. Given n, the first part of the recursive-call tree looks as follows (where we denote by “Ps” the Proof-search algorithm)
is built in an actual exponential number of calls. Given n, the first part of the recursive-call tree looks as follows (where we denote by “Ps” the Proof-search algorithm)

where  . So, any call of the shape
. So, any call of the shape  produces two calls
produces two calls  and
and  with \(\varGamma '\ne \varGamma ''\); overall there are at least \(2^n\) calls.
with \(\varGamma '\ne \varGamma ''\); overall there are at least \(2^n\) calls.
However, the complexity of the compliance decision procedure can be drastically reduced down to a polynomial complexity as detailed below.
A polynomial decision algorithm.
We first define a non-well founded, but equivalent version of system \(\vartriangleright \).
Definition 13
(The non-well founded system  ). We write
). We write  whenever there exists a finite or infinite derivation tree formed by the rules in Fig. 6 having
whenever there exists a finite or infinite derivation tree formed by the rules in Fig. 6 having  as conclusion, and such that each finite branch ends with an instance of axiom \(({{\textsc {Ax}}}_\infty )\).
as conclusion, and such that each finite branch ends with an instance of axiom \(({{\textsc {Ax}}}_\infty )\).
Lemma 1
(Systems \(\vartriangleright \) and  are equivalent).
are equivalent). 
In Fig. 7 we present a decision algorithm  , based on the procedures \(\mathbf P \) and \(\mathbf P \!^{\varvec{+}}\). A run of the algorithm resembles a computation tree of an alternating Turing machine, where nodes corresponding to rules \((\oplus \cdot +_\infty )\) and \((+\cdot \oplus _\infty )\) are universal, and nodes corresponding to \((+\cdot +_\infty )\) are existential; \(\mathbf P (\textsf {A}, \mathsf {F}, \mathsf {L}, \mathsf {b})\) attempts to prove all statements in its goal list \(\mathsf {L}\), while \(\mathbf P \!^{\varvec{+}}(\textsf {A}, \mathsf {F}, \mathsf {L}, \mathsf {b})\) succeeds if at least one goal in \(\mathsf {L}\) is satisfiable.
, based on the procedures \(\mathbf P \) and \(\mathbf P \!^{\varvec{+}}\). A run of the algorithm resembles a computation tree of an alternating Turing machine, where nodes corresponding to rules \((\oplus \cdot +_\infty )\) and \((+\cdot \oplus _\infty )\) are universal, and nodes corresponding to \((+\cdot +_\infty )\) are existential; \(\mathbf P (\textsf {A}, \mathsf {F}, \mathsf {L}, \mathsf {b})\) attempts to prove all statements in its goal list \(\mathsf {L}\), while \(\mathbf P \!^{\varvec{+}}(\textsf {A}, \mathsf {F}, \mathsf {L}, \mathsf {b})\) succeeds if at least one goal in \(\mathsf {L}\) is satisfiable.
The Provability procedure \(\mathbf P \) is an adaptation of the concrete subtyping algorithm for recursive arrow and product types of [20](Sect. 10) to the present, more complex context. It consists of a proof reconstruction procedure for  using a depth-first technique. \(\mathbf P \) accumulates in its first argument \(\textsf {A}\) all the judgments it encounters during the search, in order to avoid looping over the same judgments (a role similar to \(\varGamma \) in system \(\vartriangleright \)). With respect to the algorithm in [20](Sect. 10) we have two further parameters, \(\mathsf {F}\) and \(\mathsf {b}\). The argument \(\mathsf {F}\) accumulates the judgments for which it has been found that no derivation exists. When a rule (\(+\cdot +\)) is encountered, the algorithm proceeds by calling the procedure \(\mathbf P \!^{\varvec{+}}\) which, in case a premise is unprovable, goes on checking the other premises. The negative information inferred about unprovable judgments is stored in \(\mathsf {F}\) and it is carried along by the procedure \(\mathbf P \!^{\varvec{+}}\) (as well as the positive information stored in \(\textsf {A}\)) in order not to duplicate work. The argument \(\mathsf {b}\), that can be either \(\mathbf{ok }\) or \(\mathbf{fail }\), is used to record whether the last call was successful or not, and it is used by \(\mathbf P \!^{\varvec{+}}\) to know whether it has to stop with success, or to check a new premise.
using a depth-first technique. \(\mathbf P \) accumulates in its first argument \(\textsf {A}\) all the judgments it encounters during the search, in order to avoid looping over the same judgments (a role similar to \(\varGamma \) in system \(\vartriangleright \)). With respect to the algorithm in [20](Sect. 10) we have two further parameters, \(\mathsf {F}\) and \(\mathsf {b}\). The argument \(\mathsf {F}\) accumulates the judgments for which it has been found that no derivation exists. When a rule (\(+\cdot +\)) is encountered, the algorithm proceeds by calling the procedure \(\mathbf P \!^{\varvec{+}}\) which, in case a premise is unprovable, goes on checking the other premises. The negative information inferred about unprovable judgments is stored in \(\mathsf {F}\) and it is carried along by the procedure \(\mathbf P \!^{\varvec{+}}\) (as well as the positive information stored in \(\textsf {A}\)) in order not to duplicate work. The argument \(\mathsf {b}\), that can be either \(\mathbf{ok }\) or \(\mathbf{fail }\), is used to record whether the last call was successful or not, and it is used by \(\mathbf P \!^{\varvec{+}}\) to know whether it has to stop with success, or to check a new premise.
Let us note that, contrary to the previous treatment, while studying the algorithm  , we abandon the equi-recursive view of recursion, and we represent a contract by a particular explicit (possibly) recursive expression.
, we abandon the equi-recursive view of recursion, and we represent a contract by a particular explicit (possibly) recursive expression.
Proposition 6
(Complexity of Deciding Compliance/Subcontract).
Given two contracts \(\rho ,\sigma \in \mathbf {rs}\mathsf {C}\), deciding whether  (or \(\rho \preccurlyeq _s\sigma \)) holds has a complexity \(\mathcal {O}(n^5)\), where n is the maximum size of \(\rho \) and \(\sigma \).
(or \(\rho \preccurlyeq _s\sigma \)) holds has a complexity \(\mathcal {O}(n^5)\), where n is the maximum size of \(\rho \) and \(\sigma \).
Remark 4
It is worth noticing that the polynomial decision procedure  applies also to the formalism of retractable session contracts of [7] (in this case clauses at lines -8- and -12- are never used) and to the formalism of sessions contracts (some more clauses are never used).
applies also to the formalism of retractable session contracts of [7] (in this case clauses at lines -8- and -12- are never used) and to the formalism of sessions contracts (some more clauses are never used).
6 Related Work and Conclusion
We have presented two conservative extensions of the session contracts of [2, 3, 10], a formalism interpreting session types [22] into a subset of contracts [14, 15, 27]. One extension deals with backtracking and one with speculative execution. We have shown that they both give rise to the same compliance relation, and, as a consequence, to the same subcontract (both for servers and for clients) and duality relations. For each of these relations we provided syntactic characterizations of the semantic concepts, allowing for efficient ways of checking them.
We discussed in the Introduction the improvements w.r.t. the preliminary results about retractable session contracts in [7]. Another closely related work is [5, 6], where a different form of contracts with rollback is presented. Our retractable contracts depart from that model on three main aspects: (1) we use rollback in a disciplined way to tolerate failures in the interaction (in [5, 6] it is an internal decision of a participant), thus improving compliance; (2) we embed checkpoints in the structure of contracts, avoiding explicit checkpoints; (3) we keep a stack of “pasts”, instead of just a single past as in [5, 6].
Reversibility, generalizing backtracking by allowing one to go back to any past state, has also been studied in the setting of binary session types [32, 33]. There however the emphasis is on defining the reversible engine, based on causal-consistent reversibility [26], and not on studying compliance or subtyping (which would correspond to our subcontract relation).
Similarly to our retractable contracts, long running transactions with compensations, and in particular interacting transactions [18], allow one to undo past agreements. In interacting transactions, however, abort (which corresponds to our backtracking) can occur at any time, not only when an agreement cannot be found as in our case. Also, each transaction offers just two possibilities, and they are sorted: first the normal execution, then the compensation. Finally, compliance of interacting transactions has never been studied.
In [4] a game-theoretical interpretation of the retractable session contracts of [7] has been provided. Such an interpretation is likely to extend to the retractable contracts presented here.
We plan also to investigate whether our approach can be extended to multi-party sessions [23]. An investigation of multi-party sessions with rollbacks and named checkpoints has been already undertaken in [19]. In such a paper, however, the cause of a rollback is not a synchronization failure, but it is completely transparent to the calculus. Moreover, chosen branches are not discarded and can be retried upon rollback.
Because of the relevance of higher-order features in type systems, and of session delegation in type systems with sessions in particular, also higher-order session contracts, i.e. session contracts with delegation, have been investigated [3, 11]. It is hence worth studying the integration of backtracking (or speculative execution) and session delegation.
A last line of future work is the study of how to extract retractable or speculative contracts from actual software based on backtracking or on speculative parallelism, and how to propagate the results on contracts to the original software.
References
Avizienis, A., Laprie, J.-C., Randell, B., Landwehr, C.E.: Basic concepts and taxonomy of dependable and secure computing. IEEE Trans. Dep. Sec. Comput. 1(1), 11–33 (2004)
Barbanera, F., de’Liguoro, U.: Two notions of sub-behaviour for session-based client/server systems. In: PPDP, pp. 155–164. ACM Press (2010)
Barbanera, F., Liguoro, U.: Sub-behaviour relations for session-based client/server systems. MSCS 25(6), 1339–1381 (2015)
Barbanera, F., de’Liguoro, U.: A game interpretation of retractable contracts. In: Lluch Lafuente, A., Proença, J. (eds.) COORDINATION 2016. LNCS, vol. 9686, pp. 18–34. Springer, Cham (2016). doi:10.1007/978-3-319-39519-7_2
Barbanera, F., Dezani-Ciancaglini, M., de’Liguoro, U.: Compliance for reversible client/server interactions. In: BEAT, EPTCS, vol. 162, pp. 35–42 (2014)
Barbanera, F., Dezani-Ciancaglini, M., de’Liguoro, U.: Reversible client/server interactions. Formal Asp. Comput. 28(4), 697–722 (2016)
Barbanera, F., Dezani-Ciancaglini, M., Lanese, I., de’Liguoro, U.: Retractable contracts. In: PLACES 2015, EPTCS, vol. 203, pp. 61–72. Open Publishing Association (2016)
Barbanera, F., Lanese, I., de’Liguoro, U.: Retractable and speculative contracts (TR) (2017). http://www.cs.unibo.it/~lanese/tmp/TR-coord2017.pdf
Bartoletti, M., Cimoli, T., Murgia, M., Podda, A.S., Pompianu, L.: Compliance and subtyping in timed session types. In: Graf, S., Viswanathan, M. (eds.) FORTE 2015. LNCS, vol. 9039, pp. 161–177. Springer, Cham (2015). doi:10.1007/978-3-319-19195-9_11
Bernardi, G.T., Hennessy, M.: Modelling session types using contracts. Math. Struct. Comput. Sci. 26(3), 510–560 (2016)
Bernardi, G.T., Hennessy, M.: Using higher-order contracts to model session types. Logical Methods Comput. Sci. 12(2), 1–43 (2016)
Carbone, M., Honda, K., Yoshida, N.: Structured interactional exceptions in session types. In: Breugel, F., Chechik, M. (eds.) CONCUR 2008. LNCS, vol. 5201, pp. 402–417. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85361-9_32
Carothers, C.D., Perumalla, K.S., Fujimoto, R.: Efficient optimistic parallel simulations using reverse computation. ACM Trans. Model. Comput. Simul. 9(3), 224–253 (1999)
Carpineti, S., Castagna, G., Laneve, C., Padovani, L.: A formal account of contracts for web services. In: Bravetti, M., Núñez, M., Zavattaro, G. (eds.) WS-FM 2006. LNCS, vol. 4184, pp. 148–162. Springer, Heidelberg (2006). doi:10.1007/11841197_10
Castagna, G., Gesbert, N., Padovani, L.: A theory of contracts for web services. ACM Trans. Prog. Lang. Syst. 31(5), 19:1–19:61 (2009)
Preda, M., Gabbrielli, M., Lanese, I., Mauro, J., Zavattaro, G.: Graceful interruption of request-response service interactions. In: Kappel, G., Maamar, Z., Motahari-Nezhad, H.R. (eds.) ICSOC 2011. LNCS, vol. 7084, pp. 590–600. Springer, Heidelberg (2011). doi:10.1007/978-3-642-25535-9_45
Danos, V., Krivine, J.: Reversible communicating systems. In: Gardner, P., Yoshida, N. (eds.) CONCUR 2004. LNCS, vol. 3170, pp. 292–307. Springer, Heidelberg (2004). doi:10.1007/978-3-540-28644-8_19
Vries, E., Koutavas, V., Hennessy, M.: Communicating transactions. In: Gastin, P., Laroussinie, F. (eds.) CONCUR 2010. LNCS, vol. 6269, pp. 569–583. Springer, Heidelberg (2010). doi:10.1007/978-3-642-15375-4_39
Dezani-Ciancaglini, M., Giannini, P.: Reversible multiparty sessions with checkpoints. In: EXPRESS/SOS 2016, EPTCS, vol. 222, pp. 60–74 (2016)
Gapeyev, V., Levin, M.Y., Pierce, B.C.: Recursive subtyping revealed. J. Funct. Program. 12(6), 511–548 (2002)
Hoare, C.A.R.: Communicating Sequential Processes. Prentice-Hall, New York (1985)
Honda, K., Vasconcelos, V.T., Kubo, M.: Language primitives and type discipline for structured communication-based programming. In: Hankin, C. (ed.) ESOP 1998. LNCS, vol. 1381, pp. 122–138. Springer, Heidelberg (1998). doi:10.1007/BFb0053567
Honda, K., Yoshida, N., Carbone, M.: Multiparty asynchronous session types. In: POPL, pp. 273–284. ACM Press (2008)
Hüttel, H., et al.: Foundations of session types and behavioural contracts. ACM Comput. Surv. 49(1), 3:1–3:36 (2016)
Lanese, I., Mezzina, C.A., Stefani, J.-B.: Reversibility in the higher-order \(\pi \)-calculus. Theor. Comput. Sci. 625, 25–84 (2016)
Lanese, I., Mezzina, C.A., Tiezzi, F.: Causal-consistent reversibility. Bull. EATCS 114 (2014)
Laneve, C., Padovani, L.: The must preorder revisited. In: Caires, L., Vasconcelos, V.T. (eds.) CONCUR 2007. LNCS, vol. 4703, pp. 212–225. Springer, Heidelberg (2007). doi:10.1007/978-3-540-74407-8_15
Padovani, L.: Contract-based discovery of web services modulo simple orchestrators. Theoret. Comput. Sci. 411, 3328–3347 (2010)
Phillips, I.C.C., Ulidowski, I.: Reversing algebraic process calculi. J. Logic Alg. Program. 73(1–2), 70–96 (2007)
Prabhu, P., Ramalingam, G., Vaswani, K.: Safe programmable speculative parallelism. In: PLDI, pp. 50–61. ACM (2010)
Quiñones, C.G., et al.: Mitosis compiler: an infrastructure for speculative threading based on pre-computation slices. In: PLDI, pp. 269–279. ACM (2005)
Tiezzi, F., Yoshida, N.: Towards reversible sessions. In: PLACES, EPTCS, vol. 155. pp. 17–24 (2014)
Tiezzi, F., Yoshida, N.: Reversible session-based pi-calculus. J. Log. Algebr. Meth. Program. 84(5), 684–707 (2015)
Xu, L., Hutter, F., Hoos, H.H., Leyton-Brown, K.: Satzilla: Portfolio-based algorithm selection for SAT. J. Artif. Intell. Res. (JAIR) 32, 565–606 (2008)
Zhang, L., Malik, S.: The quest for efficient boolean satisfiability solvers. In: Brinksma, E., Larsen, K.G. (eds.) CAV 2002. LNCS, vol. 2404, pp. 17–36. Springer, Heidelberg (2002). doi:10.1007/3-540-45657-0_2
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 IFIP International Federation for Information Processing
About this paper
Cite this paper
Barbanera, F., Lanese, I., de’Liguoro, U. (2017). Retractable and Speculative Contracts. In: Jacquet, JM., Massink, M. (eds) Coordination Models and Languages. COORDINATION 2017. Lecture Notes in Computer Science(), vol 10319. Springer, Cham. https://doi.org/10.1007/978-3-319-59746-1_7
Download citation
DOI: https://doi.org/10.1007/978-3-319-59746-1_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-59745-4
Online ISBN: 978-3-319-59746-1
eBook Packages: Computer ScienceComputer Science (R0)








 on contracts with history is defined by:
on contracts with history is defined by: 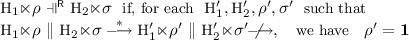
 on contracts is defined by:
on contracts is defined by: