Abstract
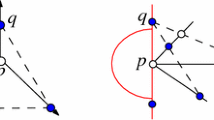
In this paper we show that the problem of deciding whether the visibility graph of a point set is 5-colourable, is NP-complete. We give an example of a point visibility graph that has chromatic number 6 while its clique number is only 4.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Cardinal, J., Hoffmann, U.: Recognition and complexity of point visibility graphs. In: Symposium of Computational Geometry, pp. 171–185 (2015)
Chazelle, B., Guibas, L.J., Lee, D.T.: The power of geometric duality. BIT 25, 76–90 (1985)
Cibulka, J., Kyncl, J., Valtr, P.: On planar point sets with the pentagon property. In: Proceedings of the Twenty-Ninth Annual Symposium on Computational Geometry, pp. 81–90 (2013)
De Berg, M., Cheong, O., Kreveld, M., Overmars, M.: Computational Geometry, Algorithms and Applications, 3rd edn. Springer, Heidelberg (2008)
Diwan, A.A., Roy, B.: Partitions of planar point sets into polygons. In: Proceedings of the 28th Canadian Conference on Computational Geometry, pp. 147–154 (2016)
Edelsbrunner, H., O’Rourke, J., Seidel, R.: Constructing arrangements of lines and hyperplanes with applications. SIAM J. Comput. 15, 341–363 (1986)
Garey, M.R., Johnson, D.S.: Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H Freeman and Company, New York (1979)
Ghosh, S.K.: Visibility Algorithms in the Plane. Cambridge University Press, New York (2007)
Ghosh, S.K., Goswami, P.P.: Unsolved problems in visibility graphs of points, segments and polygons. ACM Comput. Surv. 46(2), 22:1–22:29 (2013)
Ghosh, S.K., Roy, B.: Some results on point visibility graphs. Theor. Comput. Sci. 575, 17–32 (2015)
Kára, J., Pór, A., Wood, D.R.: On the chromatic number of the visibility graph of a set of points in the plane. Discret. Comput. Geom. 34(3), 497–506 (2005)
Lozano-Perez, T., Wesley, M.A.: An algorithm for planning collision-free paths among polyhedral obstacles. Commun. ACM 22, 560–570 (1979)
Mycielski, J.: Sur le coloriage des graphes. Colloq. Math. 3, 161–162 (1955)
Payne, M.S., Pór, A., Valtr, P., Wood, D.R.: On the connectivity of visibility graphs. Discret. Comput. Geom. 48(3), 669–681 (2012)
Pfender, F.: Visibility graphs of point sets in the plane. Discret. Comput. Geom. 39(1), 455–459 (2008)
Roy, B.: Point visibility graph recognition is NP-hard. Int. J. Comput. Geom. Appl. 26(1), 1–32 (2016)
Shapiro, L.G., Haralick, R.M.: Decomposition of two-dimensional shape by graph-theoretic clustering. IEEE Trans. Pattern Anal. Mach. Intell. PAMI-1, 10–19 (1979)
Acknowledgements
The authors are grateful to the referees for their valuable comments and specially pointing out reference [15].
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Diwan, A.A., Roy, B. (2017). On Colouring Point Visibility Graphs. In: Gaur, D., Narayanaswamy, N. (eds) Algorithms and Discrete Applied Mathematics. CALDAM 2017. Lecture Notes in Computer Science(), vol 10156. Springer, Cham. https://doi.org/10.1007/978-3-319-53007-9_14
Download citation
DOI: https://doi.org/10.1007/978-3-319-53007-9_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-53006-2
Online ISBN: 978-3-319-53007-9
eBook Packages: Computer ScienceComputer Science (R0)