Abstract
In this paper we explore the design of sequent calculi operating on graphs. For this purpose, we introduce logical connectives allowing us to extend the well-known correspondence between classical propositional formulas and cographs. We define sequent systems operating on formulas containing such connectives, and we prove, using an analyticity argument based on cut-elimination, that our systems provide conservative extensions of multiplicative linear logic (without and with mix) and classical propositional logic. We conclude by showing that one of our systems captures graph isomorphism as logical equivalence and that it is sound and complete for the graphical logic \(\textsf{GS}\).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
In theoretical computer science, formulas play a crucial role in describing complex abstract objects. At the syntactical level, the formulas of a logic describe complex structures by means of unary and binary operators, usually thought of as connectives and modalities respectively. On the other hand, graph-based syntaxes are often favored in formal representation, as they provide an intuitive and canonical description of properties, relations and systems. By means of example, consider the two graphs below:

It follows from results in [21, 62] that describing any of the above graphs by means of formulas only employing binary connectives would require repeating at least one vertex. As a consequence, formulas describing complex graphs are usually long and convoluted, and specific encodings are needed to standardize such formulas.
Since graphs are ubiquitous in theoretical computer science and its applications, a natural question to ask is whether it is possible to define formalisms having graphs, instead of formulas, as first-class terms of the syntax. Such a paradigm shift would allow the design of efficient automated tools, reducing the need to handle the bureaucracy introduced in order to deal with the encoding required to represent graphs. At the same time, a graphical syntax would provide a useful tool for investigations such as the ones in [36] or [25, 27], where the authors restrain their framework to sequential-parallel orders, as these can be represented by means of formulas with at most binary connectives.
Two recent lines of work have generalized proof theoretical methodologies to graphs, extending the correspondence between classical propositional formulas and cographs. In these works, systems operating on graphs are defined via local and context-free rewriting rules, similar to the approach in deep inference systems [8, 33, 34]. The first line of research, carried out by Calk, Das, Rice and Waring in various works, explores the use of maximal stable sets/cliques-preserving homomorphisms to define notions of entailmentFootnote 1, and study the resulting proof theory [16, 17, 23, 24, 63]. Here, the use of a deep inference formalism is natural, since the rules of the calculus are local rewritings. The second line of research, investigated by the author, Horne, Mauw and Straßburger in several contributions [3,4,5], studies the (sub-)structural proof theory of arbitrary graphs, with an approach inspired by linear logic [29] and deep inference [33]. The main goal of this line of research, partially achieved with the system \(\mathsf {GV^{sl}}\) operating on mixed graphs [3], is to obtain a generalization of the completeness result of the logic \(\textsf{BV}\) with respect to pomset inclusion. The logic \(\textsf{BV}\) contains a non-commutative binary connective \(\triangleleft \) allowing to represent series-parallel partial order multisets as formulas in the syntax (as in Retoré’s \(\textsf{Pomset}\) logic [57]), and to capture order inclusion as logical implication. However, as shown in [60], no cut-free sequent system for \(\textsf{BV}\) can exist – therefore neither for \(\textsf{Pomset}\) logic, which strictly contains it [53, 54]. For this reason, the aforementioned line of work focused on deep inference systems, and the question about the existence of a cut-free sequent calculus for \(\textsf{GS}\) (the restriction of \(\mathsf {GV^{sl}}\) on undirected graphs originally defined in [4]) was left open.
In this paper, we focus on the definition of sequent calculi for graphical logics, and we positively answer the above question by providing, among other results, a cut-free sound and complete sequent calculus for \(\textsf{GS}\). By using standard techniques in sequent calculus, we thus obtain a proof of analyticity for this logic which is simpler and more concise with respect to the one in [5].
To achieve these results, we introduce graphical connectives, which are operators that can be naturally interpreted as graphs. We then define the sequent calculi \(\textsf{MGL}\), \(\textsf{MGL}^\circ \) and \(\textsf{KGL}\), containing rules to handle these connectives. After showing that cut-elimination holds for these systems, we prove that \(\textsf{MGL}\), \(\textsf{MGL}^\circ \) and \(\textsf{KGL}\) define conservative extensions of multiplicative linear logic, multiplicative linear logic with mix and classical propositional logic respectively. We then prove that formulas interpreted as the same graph are logically equivalent, thus justifying the fact that we consider these systems as operating on graphs rather than formulas. We conclude by showing that \(\textsf{MGL}^\circ \) is sound and complete with respect to the logic \(\textsf{GS}\), thus providing a simple sequent calculus for the logic.
The paper is structured as follows. In Sect. 2 we show how to use the notion of modular decomposition for graphs from [28, 41] to define graphical connectives. In this way, we extend to general graphs the well-known correspondence between classical propositional formulas and cographs [21, 28, 41]. Then, in Sect. 3, we introduce the proof systems \(\textsf{MGL}\), \(\textsf{MGL}^\circ \) and \(\textsf{KGL}\), and we prove their cut-elimination and analyticity. This section also discusses the conservativity results. In Sect. 4 we show that formulas representing isomorphic graphs are logically equivalent in these logics. Finally, in Sect. 5 we prove that \(\textsf{MGL}^\circ \) is sound and complete with respect to the graphical logic \(\textsf{GS}\). We conclude with Sect. 6, by discussing future research directions and applications. Due to space limitations, details of certain proofs have been omitted from this manuscript However, detailed proofs can be found in [2].
2 From Graphs to Formulas
In this section we first recall standard results from the literature on graphs, the notion of modular decomposition and the one of cographs, which are graphs whose modular decomposition only contains two prime graphs which can be naturally interpreted as (binary) conjunction and disjunction. We then introduce the notion of graphical connectives, allowing us to extend the correspondence between cographs and propositional formulas to general graphs, allowing us to represent graphs via formulas constructed using graphical connectives.
2.1 Graphs and Modules
In this work are interested in using (labeled) graphs to represent patterns of interactions by means of the binary relations (edges) between their components (vertices). We recall the standard notion of identity on labeled graphs (i.e., isomorphism) and define the rougher notion of similarity (isomorphism up-to vertex labels).
Definition 1
A \(\boldsymbol{\mathcal {L}}\) -labeled graph (or simply graph)
 is given by a finite set of vertices \(V_{G}\), a partial labeling function \(\ell _G:V_{G}\rightarrow \mathcal {L}\) associating a label \(\ell _{}(v)\) from a given set of labels \(\mathcal {L}\) to each vertex \(v\in V_{G}\) (we may represent \(\ell _G\) as a set of equations of the form \(\ell _{}(v)= \ell _v \) and denote by \(\varnothing \) the empty function), and a non-reflexive symmetric edge relation
is given by a finite set of vertices \(V_{G}\), a partial labeling function \(\ell _G:V_{G}\rightarrow \mathcal {L}\) associating a label \(\ell _{}(v)\) from a given set of labels \(\mathcal {L}\) to each vertex \(v\in V_{G}\) (we may represent \(\ell _G\) as a set of equations of the form \(\ell _{}(v)= \ell _v \) and denote by \(\varnothing \) the empty function), and a non-reflexive symmetric edge relation
 whose elements, called edges, may be denoted vw instead of (v, w). The empty graph \(\langle \varnothing ,\varnothing ,\varnothing \rangle \) is denoted \(\varnothing \) and we define the edge relation
whose elements, called edges, may be denoted vw instead of (v, w). The empty graph \(\langle \varnothing ,\varnothing ,\varnothing \rangle \) is denoted \(\varnothing \) and we define the edge relation
 .
.
A similarity between two graphs \(G\) and \(G'\) is a bijection \(f:V_{G}\rightarrow V_{G'}\) such that
 iff
iff
 for any \(x,y\in V_{G}\). A symmetry is a similarity of a graph with itself. An isomorphism is a similarity f such that \(\ell _{}(v)=\ell _{}(f(v))\) for any \(v\in V_{G}\). Two graphs \(G\) and \(G'\) are similar (denoted \(G\sim _{}G'\)) if there is a similarity between \(G\) and \(G'\). They are isomorphic (denoted \(G=G'\)) if there is an isomorphism between \(G\) and \(G'\). From now on, we consider two isomorphic graphs to be the same graph.
for any \(x,y\in V_{G}\). A symmetry is a similarity of a graph with itself. An isomorphism is a similarity f such that \(\ell _{}(v)=\ell _{}(f(v))\) for any \(v\in V_{G}\). Two graphs \(G\) and \(G'\) are similar (denoted \(G\sim _{}G'\)) if there is a similarity between \(G\) and \(G'\). They are isomorphic (denoted \(G=G'\)) if there is an isomorphism between \(G\) and \(G'\). From now on, we consider two isomorphic graphs to be the same graph.
Two vertices v and w in \(G\) are connected if there is a sequence \(v=u_0,\ldots , u_n=w\) of vertices in \(G\) (called path) such that
 for all \(i\in \{1,\ldots ,n\}\). A connected component of \(G\) is a maximal set of connected vertices in \(G\). A graph \(G\) is a clique (resp. a stable set) iff
for all \(i\in \{1,\ldots ,n\}\). A connected component of \(G\) is a maximal set of connected vertices in \(G\). A graph \(G\) is a clique (resp. a stable set) iff
 (resp.
(resp.
 ).
).
Note 1
When drawing a graph or an unlabeled graph we draw
 whenever
whenever
 , we draw no edge at all whenever
, we draw no edge at all whenever
 . We may represent a vertex by using its label instead of its name. For example, the single-vertex graph \(G=\langle \{v\},\ell _G,\varnothing \rangle \) may be represented either by the vertex (name) v or by the vertex label \(\ell _G(v)\) (in this case we may write \(\bullet \) if \(\ell _G(v) \) is not defined).
. We may represent a vertex by using its label instead of its name. For example, the single-vertex graph \(G=\langle \{v\},\ell _G,\varnothing \rangle \) may be represented either by the vertex (name) v or by the vertex label \(\ell _G(v)\) (in this case we may write \(\bullet \) if \(\ell _G(v) \) is not defined).
Example 1
Consider the following graphs:

We have \(F\sim _{}G\sim _{}H\) and
 .
.
Note 2
Whenever we say that two graphs are the same, we assume they share the same set of vertices and labeling function, therefore implicitly assuming the isomorphism f to be given. This allows us to verify whether two graphs are isomorphic (i.e., the same) in polynomial time on the number of vertices.
We recall the notion of module [26, 28, 35, 41, 45, 48], allowing us to represent a graph using a tree-like syntax. A module is a subset of vertices of a graph having the same edge-relation with any vertex outside the subset, generalizing what can usually be observed in formulas, where, in the formula tree, each literal in a subformula has the same least common ancestor with a given literal not belonging to the subformula itself.
Definition 2
Let \(G=\langle V_{G},\ell _G,E_G\rangle \) be a graph and \(W\subseteq V_{G}\). The graph induced by W is the graph
 where \(\ell _G|_{W}(v){:}{=}\ell _G(v)\) for all \(v\in W\).
where \(\ell _G|_{W}(v){:}{=}\ell _G(v)\) for all \(v\in W\).
A module of a graph \(G\) is a subset M of \(V_{G}\) such that
 iff
iff
 for any \(x,y\in M\), \(z\in V_{G}\setminus M\). A module M is trivial if \(M=\varnothing \), \(M=V_{G}\), or \(M=\{x\}\) for some \(x\in V_{G}\). From now on, we identify a module \(M\) of a graph \(G\) with the induced subgraph \(G|_{M}\).
for any \(x,y\in M\), \(z\in V_{G}\setminus M\). A module M is trivial if \(M=\varnothing \), \(M=V_{G}\), or \(M=\{x\}\) for some \(x\in V_{G}\). From now on, we identify a module \(M\) of a graph \(G\) with the induced subgraph \(G|_{M}\).
Remark 1
A connected component of a graph \(G\) is a module of \(G\).
Note 3
We may optimize graph representations by bordering vertices of a same module by a closed line. An edge connected to such a closed line denotes the existence of an edge to each vertex inside it (see Fig. 1). By means of example, consider the following graph and its more compact modular representation.

The notion of module is related to a notion of context, which can be intuitively formulated as a graph with a “hole”.
Definition 3
A context \(\mathcal {C}[\Box ]\) is a (non-empty) graph containing a single occurrence of a special vertex \(\Box \) (with \(\ell _{}(\Box )\) undefined). It is trivial if \(\mathcal {C}[\Box ]=\Box \). If \(\mathcal {C}[\Box ]\) is a context and \(G\) a graph, we define \(\mathcal {C}[G]\) as the graph obtained by replacing \(\Box \) by \(G\). Formally,

Remark 2
The notion of context and the one of module are interdefinable. In fact, a set of vertices \(M\) is a module of a graph \(G\) iff there is a context \(\mathcal {C}[\Box ]\) such that \(G=\mathcal {C}[M]\).
Note that \(M\) is a module of a graph \(G\) iff there is a context \(\mathcal {C}[\Box ]\) such that \(G=\mathcal {C}[M]\). We generalize this idea of replacing a vertex of a graph with a module by defining the operations of composition-via a graph, where all vertices of a graph are replaced in a “modular way” by modules.
Definition 4
Let \(G\) be a graph with \(V_{G}=\{v_1,\ldots ,v_n\}\) and let \(H_1,\ldots ,H_n\) be graphs. We define the composition of \(H_1,\ldots ,H_n\) via \(G\) as the graph \(G\llparenthesis H_1,\ldots ,H_n\rrparenthesis \) obtained by replacing each vertex \(v_i\) of \(G\) with a module \(H_i\) for all \(i\in \{1,\ldots ,n\}\). Formally,

The subgraphs \(H_1,\ldots , H_n\) are called factors of \(G\llparenthesis H_1,\ldots , H_n\rrparenthesis \) and, by definition, are (possibly not maximal) modules of \(G\llparenthesis H_1,\ldots , H_n\rrparenthesis \).
Remark 3
The operation of composition-via \(G\) forgets the information carried by the labeling function \(\ell _G\). Moreover, if \(\sigma \) is a similitude between two graphs \(G\) and \(G'\), then \(G\llparenthesis H_1,\ldots ,H_n\rrparenthesis =G'\llparenthesis H_{\sigma (1)},\ldots ,H_{\sigma (n)}\rrparenthesis \).
In order to establish a connection between graphs and formulas, from now on we only consider graphs whose set of labels belong to the set \(\mathcal {L}=\left\{ a,a^\bot \mid a\in \mathcal {A}\right\} \) where \(\mathcal {A}\) is a fixed set of propositional variables. We then define the dual of a graph.
Definition 5
Let \(G=\langle V_{G},\ell _G,E_G\rangle \) be a graph. We define the dual graph of \(G\) as the graph
 with \(\ell _{G^\bot }(v)=\left( \ell _G(v)\right) ^\bot \) (assuming \(a^{\bot \bot }=a\) for all \(a\in \mathcal {A}\)).
with \(\ell _{G^\bot }(v)=\left( \ell _G(v)\right) ^\bot \) (assuming \(a^{\bot \bot }=a\) for all \(a\in \mathcal {A}\)).
2.2 Classical Propositional Formulas as Cographs
The set of classical (propositional) formulas is generated from a set of propositional variable \(\mathcal {A}\) using the negation \((\cdot )^\bot \), the disjunction \(\vee \) and the conjunction \(\wedge \) using the following grammar:
We define a map from literals to single-vertex graphs, which extends to formulas via the composition-via the unlabeled two-vertices stable set and two-vertices clique.
Definition 6
Let \(\phi \) be a classical formula, and let \(\textsf{S}_2=\langle \{v_1, v_2\},\varnothing ,\varnothing \rangle \) and \(\textsf{K}_2=\langle \{v_1, v_2\},\varnothing ,\{v_1v_2\}\rangle \). We define the graph \(\left[ \!\left[ \phi \right] \!\right] \) as follows:
where we denote by a the single-vertex graph, whose vertex is labeled by a. A cograph is a graph \(G\) such that there is a classical formula \(\phi \) such that \(G=\left[ \!\left[ \phi \right] \!\right] \).
Example 2
Let \(\phi \) and \(\psi \) classical formulas containing occurrences of atoms \(\{a_1,\ldots , a_n\}\) and \(\{b_1,\ldots b_m\}\) respectively. Then the graph \(\left[ \!\left[ \phi \wedge \psi \right] \!\right] \) can be represented as follows:

Note that an equivalent definition of cographs can be given using only the graph \(\textsf{S}_2\) (or \(\textsf{K}_2\)) and duality.
We can easily observe that the map \(\left[ \!\left[ \cdot \right] \!\right] \) well-behaves with respect to the equivalence over formulas generated by the associativity and commutativity of connectives and the de Morgan laws below.

Proposition 1
Let \(\phi \) and \(\psi \) be classical formulas. Then \(\phi \equiv \psi \) iff \(\left[ \!\left[ \phi \right] \!\right] =\left[ \!\left[ \psi \right] \!\right] \).
We finally recall an alternative definition of cographs as graphs containing no induced subgraph of a specific shape, and we recall the theorem establishing the relation between
Definition 7
A graph \(G\) is P\(_{\boldsymbol{4}}\) -free if there it contains no four vertices \(v_1,v_2,v_3,v_4\) such that the induced subgraph \(G|_{\{v_1,v_2,v_3,v_4\}}\) is similar to the graph
 .
.
Theorem 1
([28]). Let \(G\) be a graph. Then \(G\) is a cograph iff \(G\) is \(\mathsf {P_4}\)-free.
2.3 Modular Decomposition of Graphs
We recall the notion of prime graph, allowing us to provide canonical representatives of graphs via modular decomposition. (see e.g., [26, 28, 35, 41, 45, 48]).
Definition 8
A graph \(G\) is prime if \(|V_{G}|> 1\) and all its modules are trivial.
We recall the following standard result from the literature.
Theorem 2
([41]). Let \(G\) be a graph with at least two vertices. Then there are non-empty modules \( M_1, \dots , M_n \) of \(G\) and a prime graph \(P\) such that \(G=P\llparenthesis M_1, \dots , M_n\rrparenthesis \).
This result allows us to describe graphs using its modular decomposition, that is, using single-vertex graphs and operations of composition-via prime graphs only.
Definition 9
Let \(G\) be a non-empty graph. A modular decomposition of \(G\) is a way to write \(G\) using single-vertex graphs and the operation of composition-via prime graphs:
-
if \(G\) is a graph with a single vertex x labeled by a, then \(G=a\);
-
if \(H_1, \ldots , H_n\) are maximal modules of \(G\) such that \(V_{G}=\biguplus _{i=1}^nV_{H_i}\), then there is a unique prime graph \(P\) such that \(G=P\llparenthesis H_1, \ldots , H_n\rrparenthesis \).
Ambiguity arises in modular decomposition due to the presence of cliques or stable sets with more than three vertices, graph symmetries, and the presence of symmetric but non-isomorphic graphs. The first two ambiguities are akin to the one observed in propositional logic, where conjunction and disjunction are considered associative and commutative. These are addressed similarly in the framework we discuss in this paper. However, to reduce the latter source of ambiguity, we introduce the notion of basis of graphical connectives.
Definition 10
A graphical connective
 (with arity \(n=|V_{\mathcal {C}}|\)) is given by a finite list of vertices \(V_{\mathcal {C}}=\langle v_1,\ldots ,v_n\rangle \) and a non-reflexive symmetric edge relation
(with arity \(n=|V_{\mathcal {C}}|\)) is given by a finite list of vertices \(V_{\mathcal {C}}=\langle v_1,\ldots ,v_n\rangle \) and a non-reflexive symmetric edge relation
 over the set of vertices occurring in \(V_{\mathcal {C}}\). We denote by \(G_C\) the graph corresponding to \(C\), that is, the graph
over the set of vertices occurring in \(V_{\mathcal {C}}\). We denote by \(G_C\) the graph corresponding to \(C\), that is, the graph
 . The composition-via a graphical connective is defined as the composition-via the graph \(G_C\). A graphical connective is prime if \(G_C\) is a prime graph. A set \(\mathcal {P}\) of prime graphical connectives is a basis if for each prime graph \(P\) there is a unique connective \(C\in \mathcal {P}\) such that \(P\sim G_C\).
. The composition-via a graphical connective is defined as the composition-via the graph \(G_C\). A graphical connective is prime if \(G_C\) is a prime graph. A set \(\mathcal {P}\) of prime graphical connectives is a basis if for each prime graph \(P\) there is a unique connective \(C\in \mathcal {P}\) such that \(P\sim G_C\).
Given an n-ary connective \(C\), we define the groupFootnote 2 of symmetries of \(C\) (\(\mathfrak S(C)\)) and the set of dualizing symmetries of \(C\) (\(\mathfrak S^\bot (C)\)) as the following sets of permutations over the set \(\{1,\ldots ,n\}\):
We introduce the following graphical connectives:

We can reformulate the standard result on modular decomposition as follows.
Theorem 3
Let \(G\) be a non-empty graph and \(\mathcal {P}\) a basis. Then there is a unique way (up to symmetries of graphical connectives and associativity of
 and \(\mathop \otimes \)) to write \(G\) using single-vertex graphs and the graphical connectives in \(\mathcal {P}\).
and \(\mathop \otimes \)) to write \(G\) using single-vertex graphs and the graphical connectives in \(\mathcal {P}\).
Corollary 1
Two graphs are isomorphic iff they admit a same modular decomposition.
2.4 Graphs as Formulas
In order to represent graphs as formulas, we define new connectives beyond conjunction and disjunction to represent graphical connectives in a basis \(\mathcal {P}\). From now on, we assume to be fixed a basis \(\mathcal {P}\) containing the graphical connectives in Eq. (7).
Definition 11
The set of formulas is generated by the set of propositional atoms \(\mathcal {A}\), a unit \(\circ \), and a basis of graphical connective \(\mathcal {P}\) using the following syntax:
We simply denote
 (resp. \(\mathop \otimes \)) the binary connective
(resp. \(\mathop \otimes \)) the binary connective
 (resp. \(\kappa _{\mathop \otimes }\)) and we write
(resp. \(\kappa _{\mathop \otimes }\)) and we write
 instead of
instead of
 (resp. \(\phi \mathop \otimes \psi \) instead of \(\kappa _{\mathop \otimes }\llparenthesis \phi ,\psi \rrparenthesis \)). The arity of the connective \(\kappa _{P}\) is the arity \(n_P\) of \(P\). A literal is a formula of the form a or \(a^\bot \) for an atom \(a\in \mathcal {A}\). The set of literals is denoted \(\mathcal {L}\). A formula is unit-free if it contains no occurrences of \(\circ \) and vacuous if it contains no atoms. A formula is pure if non-vacuous and such that its vacuous subformulas are \(\circ \). A MLL -formula is a formula containing only occurrences of connectives
(resp. \(\phi \mathop \otimes \psi \) instead of \(\kappa _{\mathop \otimes }\llparenthesis \phi ,\psi \rrparenthesis \)). The arity of the connective \(\kappa _{P}\) is the arity \(n_P\) of \(P\). A literal is a formula of the form a or \(a^\bot \) for an atom \(a\in \mathcal {A}\). The set of literals is denoted \(\mathcal {L}\). A formula is unit-free if it contains no occurrences of \(\circ \) and vacuous if it contains no atoms. A formula is pure if non-vacuous and such that its vacuous subformulas are \(\circ \). A MLL -formula is a formula containing only occurrences of connectives
 and \(\mathop \otimes \). A context formula (or simply context) \(\zeta [\Box ]\) is a formula containing an hole \(\Box \) taking the place of an atom. Given a context \(\zeta [\Box ]\), the formula \(\zeta [\phi ]\) is defined by simply replacing the atom \(\Box \) with the formula \(\phi \). For example, if
and \(\mathop \otimes \). A context formula (or simply context) \(\zeta [\Box ]\) is a formula containing an hole \(\Box \) taking the place of an atom. Given a context \(\zeta [\Box ]\), the formula \(\zeta [\phi ]\) is defined by simply replacing the atom \(\Box \) with the formula \(\phi \). For example, if
 , then
, then
 .
.
For each \(\phi \) formula (or context), the graph \(\left[ \!\left[ \phi \right] \!\right] \) is defined as follows:

Note 4
We may consider a formula \(\phi \) over the set of occurrences of literals \(\{x_1,\ldots ,x_n\}\) as a synthetic connective \(\phi \) with arity n. That is, we may denote by \(\phi \llparenthesis \psi _1,\ldots , \psi _n\rrparenthesis \) the formula obtained by replacing each literal \(x_i\) (with \(i\in \{1,\ldots ,n\}\)) with a formula \(\psi _i\). The set of symmetries of \(\phi \) (denoted \(\mathfrak S(\phi )\)) is the set of permutations \(\sigma \) over \(\{1,\ldots ,n\}\) such that \(\left[ \!\left[ \phi \llparenthesis x_1,\ldots ,x_n\rrparenthesis \right] \!\right] =\left[ \!\left[ \phi \llparenthesis x_{\sigma (1)},\ldots ,x_{\sigma (n)}\rrparenthesis \right] \!\right] \).
Definition 12
The equivalence relation \(\equiv \) over formulas is generated by the following:

for each \(P\in \mathcal {P}\) (with arity \(n_P=|V_{P}|\)), and for each \(\sigma \in \mathfrak S(P)\) and \(\rho \in \mathfrak S^\bot (P)\).
The (linear) negation over formulas is defined by letting
where \(Q\) is the (unique) prime connective in \(\mathcal {P}\) such that we have \(\left[ \!\left[ \kappa _{P}\llparenthesis a_1,\ldots , a_n\rrparenthesis \right] \!\right] =Q\llparenthesis a^\bot _{\sigma (1)},\ldots , a^\bot _{\sigma (n)}\rrparenthesis \) for a permutation \(\sigma \) over the set \(\{1,\ldots ,n\}\).Footnote 3
The linear implication \(\phi \multimap \psi \) is defined as
 , while the logical equivalence
, while the logical equivalence
 is defined as \((\phi \multimap \psi )\mathop \otimes (\psi \multimap \phi )\).
is defined as \((\phi \multimap \psi )\mathop \otimes (\psi \multimap \phi )\).
Remark 4
As explained in [5] (Sect. 9), the graphical connectives we discuss in this paper are multiplicative connectives (in the sense of [6, 22, 32, 47]) but they are not the same as the connectives-as-partitions discussed in these works. In fact, there is a unique 4-ary graphical connective \(\mathsf {P_4}\), which has the symmetry group \(\{\textsf{id},(1,4)(2,3)\}\), while, as shown in [6, 47], there is a unique pair of dual non-decomposable (i.e., which cannot be described using smaller connectives) 4-ary multiplicative connectives-as-partitions \(\mathsf G_4\) and \(\mathsf G_4^\bot \), and \(\mathfrak S(\mathsf {P_4})\subsetneq \mathfrak S(\mathsf G_4)=\mathfrak S(\mathsf G_4^\bot )\).
The following result is a consequence of Theorem 2.
Proposition 2
Let \(\phi \) and \(\psi \) be formulas. If \(\phi \equiv \psi \), then \(\left[ \!\left[ \phi \right] \!\right] =\left[ \!\left[ \psi \right] \!\right] \). Moreover, if \(\phi \) and \(\psi \) are unit-free, then \(\phi \equiv \psi \) iff \(\left[ \!\left[ \phi \right] \!\right] =\left[ \!\left[ \psi \right] \!\right] \).
For an example of why the equivalence result does not hold in the presence of units, consider the (non-equivalent) formulas \(\circ \mathop \otimes \circ \) and
 .
.
3 Sequent Calculi over Graphs-as-Formulas
We assume the reader to be familiar with the definition of sequent calculus derivations as trees of sequents (see, e.g., [61]) but we recall here some definitions.
Definition 13
A sequent is a set of occurrences of formulas. A sequent system \(\textsf{S}\) is a set of sequent rules as the ones in Fig. 2. A derivation (resp. open derivation) over \(\textsf{S}\) is a tree of sequents such that each node (resp. each node except some leaves, called open premises) is the conclusion of a rule with premises its children. In a sequent rule \(\textsf{r}\), we say that a formula is active (resp. principal) if it occurs in one of its premises (resp. in its conclusion) but not in its conclusion (resp. but in none of its premises) A proof of a sequent \(\varGamma \) is a derivation with root \(\varGamma \) denoted
 . We denote by
. We denote by
 an open derivation with conclusion \(\varGamma \) and a single open premise \(\varGamma '\). A rule is admissible in \(\textsf{S}\) if there is a derivation of the conclusion of the rule whenever all premises of the rule are derivable. A rule is derivable in \(\textsf{S}\), if there is a derivation in \(\textsf{S}\) from the premises to the conclusion of the rule.
an open derivation with conclusion \(\varGamma \) and a single open premise \(\varGamma '\). A rule is admissible in \(\textsf{S}\) if there is a derivation of the conclusion of the rule whenever all premises of the rule are derivable. A rule is derivable in \(\textsf{S}\), if there is a derivation in \(\textsf{S}\) from the premises to the conclusion of the rule.
Definition 14
We define the following sequent systems using the rules axiom (\(\textsf{ax}\)), par (
 ), tensor (\(\mathop \otimes \)), weakening (\(\mathsf w\)), contraction (\(\mathsf c\)), mix (\(\textsf{mix}\)), dual connectives (\(\textsf {d}-\kappa _{}\)) unitor (\(\textsf{u}_{\kappa _{}}\)), and weak-distributivity (\(\textsf{wd}_{\mathop \otimes }\)) in Fig. 2.
), tensor (\(\mathop \otimes \)), weakening (\(\mathsf w\)), contraction (\(\mathsf c\)), mix (\(\textsf{mix}\)), dual connectives (\(\textsf {d}-\kappa _{}\)) unitor (\(\textsf{u}_{\kappa _{}}\)), and weak-distributivity (\(\textsf{wd}_{\mathop \otimes }\)) in Fig. 2.

Remark 5
Rules axiom (\(\textsf{ax}\)), par (
 ), tensor (\(\mathop \otimes \)), cut (\(\textsf{cut}\)), and mix (\(\textsf{mix}\)) are the standard as in multiplicative linear logic with mix. Note that \(\textsf{ax}\) is restricted to atomic formulas. The rule \(\textsf {d}-\kappa _{}\) handles a pair of dual connectives at the same time, as it may be done by rules in focused proof systems (see, e.g. [9, 50, 51]) or rules for modalities in modal logic and linear logic (see, e.g., [12, 14, 31, 44]). Intuitively, while in standard two-sided sequent calculi the right-conjunction rule (\(\wedge _R\) below) internalizes a meta-conjunction between the premises of the rule, that is,
), tensor (\(\mathop \otimes \)), cut (\(\textsf{cut}\)), and mix (\(\textsf{mix}\)) are the standard as in multiplicative linear logic with mix. Note that \(\textsf{ax}\) is restricted to atomic formulas. The rule \(\textsf {d}-\kappa _{}\) handles a pair of dual connectives at the same time, as it may be done by rules in focused proof systems (see, e.g. [9, 50, 51]) or rules for modalities in modal logic and linear logic (see, e.g., [12, 14, 31, 44]). Intuitively, while in standard two-sided sequent calculi the right-conjunction rule (\(\wedge _R\) below) internalizes a meta-conjunction between the premises of the rule, that is,

the rule \(\textsf {d}-\kappa _{}\) internalizes a meta-\(\kappa _{}\)-connective between the premises by introducing the same connective on both sides of the sequent, as shown below in the case \(\kappa _{}=\mathsf {P_4}\).

Note that in the rule \(\wedge _R\) in Eq. (11) only a single occurrence of the connective \(\wedge \) occurs in the conclusion, on the right-hand side of \(\vdash \). This because the absence of the conjunction \(\wedge \) on the left-hand side is irrelevant since a two-sided sequent \(\varGamma \vdash \varDelta \) is interpreted as the formula \(\left( \bigwedge _{\phi \in \varGamma }\phi ^\bot \right) \vee \left( \bigvee _{\psi \in \varDelta }\psi \right) \).
The names of the rules unitor (\(\textsf{u}_{\kappa _{}}\)) and weak-distributivity (\(\textsf{wd}_{\mathop \otimes }\)) are inspired by the literature of monoidal categories [46] and weakly distributive categories [19, 20, 59]. The rule \(\textsf{u}_{\kappa _{}}\) internalizes the fact that the unit \(\circ \) is the neutral element for all connectives (its side condition prevents the creation of non-pure formulas). Under the assumption of the existence of a \(\circ \) which is the unit of both \(\mathop \otimes \) and
 , the rule \(\textsf{wd}_{\mathop \otimes }\) generalizes the weak-distributive law of the \(\mathop \otimes \) over the
, the rule \(\textsf{wd}_{\mathop \otimes }\) generalizes the weak-distributive law of the \(\mathop \otimes \) over the
 , that is,
, that is,

to the weak-distributive law of \(\mathop \otimes \) over any connective (see below on the top)

Note that an additional law is required to formalize the weak-distributive law of all connectives over
 (see the bottom of Eq. (14)). This law corresponds to the rule
(see the bottom of Eq. (14)). This law corresponds to the rule
 in Fig. 3.
in Fig. 3.
3.1 Properties of the Sequent Systems
We start by observing that these systems are initial coherent [10, 50], that is, we can derive the implication \(\phi \multimap \phi \) for any pure formula \(\phi \) only using atomic axioms. To prove this result we observe that the generalized version of \(\textsf {d}-\kappa _{}\) (that is, the rule \(\textsf {d}-\chi \)) is derivable by induction on the structure of \(\chi \) using the rule \(\textsf {d}-\kappa _{}\)
Lemma 1
Let \(\chi \) be a pure formula. Then rule \(\textsf {d}-\chi \) is derivable.
Corollary 2
The rule \(\textsf{AX}\) is derivable in \(\textsf{MGL}\) and in \(\textsf{MGL}^\circ \).
Theorem 4
\(\textsf{MGL}\), \(\textsf{MGL}^\circ \), and \(\textsf{KGL}\) are initial coherent w.r.t. pure formulas.
The admissibility of \(\textsf{cut}\) is proven via cut-elimination.
Theorem 5
Let \(\textsf{X}_{}\in \{\textsf{MGL},\textsf{MGL}^\circ ,\textsf{KGL}\}\). The rule \(\textsf{cut}\) is admissible in \(\textsf{X}_{}\).
Proof
We define the size of a formula as the sum of the number of \(\circ \), connectives and twice the number of literals in it. The size of a derivation is the sum of the sizes of the active formulas in all \(\textsf{cut}\)-rules. In Fig. 4 we only provide the less standard cut-elimination steps: the ones for \(\textsf{ax}\), \(\mathsf w\), \(\mathsf c\), and
 are the standard ones, while \(\textsf {d}-\kappa _{}-{vs}-\textsf {d}-\kappa _{}\) and \(\textsf{u}_{\kappa _{}}-{vs}-\textsf{u}_{\kappa _{}}\) (where both \(\textsf{u}_{\kappa _{}}\) rules introduce a \(\circ \) in the same “position”) are as expected, that is, by cutting each of the corresponding premises of the rules. The result for \(\textsf{MGL}\) and \(\textsf{MGL}^\circ \) follows by the fact that each cut-elimination step applied to any \(\textsf{cut}\)-rule reduces the size of a derivation, while for \(\textsf{KGL}\) we have to consider also weak-normalization result via a cut-elimination strategy prioritizing the elimination of top-most \(\textsf{cut}\)-rules.
are the standard ones, while \(\textsf {d}-\kappa _{}-{vs}-\textsf {d}-\kappa _{}\) and \(\textsf{u}_{\kappa _{}}-{vs}-\textsf{u}_{\kappa _{}}\) (where both \(\textsf{u}_{\kappa _{}}\) rules introduce a \(\circ \) in the same “position”) are as expected, that is, by cutting each of the corresponding premises of the rules. The result for \(\textsf{MGL}\) and \(\textsf{MGL}^\circ \) follows by the fact that each cut-elimination step applied to any \(\textsf{cut}\)-rule reduces the size of a derivation, while for \(\textsf{KGL}\) we have to consider also weak-normalization result via a cut-elimination strategy prioritizing the elimination of top-most \(\textsf{cut}\)-rules.
Note that to ensure that both active formulas of a \(\textsf{cut}\)-rule are principal with respect to the rule immediately above it, we also need to consider among the standard commutative cut-elimination steps (independent rule permutations) and the special step in Fig. 5. The treatment of these steps, as well as the definition of a size taking into account them, is not covered in detail here because it is standard in the literature.
Corollary 3
Let \(\textsf{X}_{}\in \{\textsf{MGL},\textsf{MGL}^\circ ,\textsf{KGL}\}\). If \(\mathord {\vdash _{\textsf{X}_{}}\,}\phi \multimap \psi \) and \(\mathord {\vdash _{\textsf{X}_{}}\,}\psi \multimap \chi \), then \(\mathord {\vdash _{\textsf{X}_{}}\,}\phi \multimap \chi \).
The admissibility of the \(\textsf{cut}\)-rule implies analyticity of \(\textsf{MGL}\) and \(\textsf{KGL}\) via the standard sub-formula property, that is, all formulas occurring in a premise of a rule are subformulas of the ones in the conclusion. However, as already observed in [3,4,5], the same result does not hold for \(\textsf{MGL}^\circ \) because the rule \(\textsf{u}_{\kappa _{}}\) and more-than-binary connectives introduce the possibility of having sub-connectives, that is, connectives with smaller arity behaving as if certain entries of the connective are fixed to be units.
Definition 15
Let \(P\) and \(Q\) be prime graphs and let \(i_1<\ldots <i_k\) be integers in \(\{1,\ldots ,|P|\}\). If \(P\llparenthesis \circ ,\ldots ,\circ , v_{i_1},\circ ,\ldots ,\circ , v_{i_k},\circ ,\ldots ,\circ \rrparenthesis \sim _{}Q\llparenthesis v_1,\dots , v_n\rrparenthesis \) for (any) single-vertex graphs \(v_1, \ldots ,v_n\), then we say that the connective \(\kappa _{Q}\) is a sub-connective of \(\kappa _{P}\) and we may write \(\kappa _{P|_{i_1,\ldots , i_k}}=\kappa _{Q}\). A quasi-subformula of a formula \(\phi =\kappa _{P}\llparenthesis \psi _1,\ldots ,\psi _n\rrparenthesis \) is a formula of the form \(\kappa _{P'|_{i_1,\ldots , i_k}}\llparenthesis \psi '_{i_1},\ldots ,\psi '_{i_k}\rrparenthesis \) with \(\psi '_{i_j}\) a quasi-subformula of \(\psi _{i_j}\) for all \(i_j\in \{i_1,\ldots ,i_k\}\).
Corollary 4
(Conservativity). \(\textsf{MGL}\) is a conservative extension of
 . \(\textsf{MGL}^\circ \) is a conservative extension of
. \(\textsf{MGL}^\circ \) is a conservative extension of
 . \(\textsf{KGL}\) is a conservative extension of \(\textsf{LK}=\textsf{MLL}\cup \{\mathsf w,\mathsf c\}\).
. \(\textsf{KGL}\) is a conservative extension of \(\textsf{LK}=\textsf{MLL}\cup \{\mathsf w,\mathsf c\}\).
Proof
The results for \(\textsf{MGL}\) and \(\textsf{KGL}\) follow from the fact that these systems satisfy the standard sub-formula property for \(\textsf{cut}\)-free derivations, therefore no connective other than
 and \(\mathop \otimes \) can be introduced during proof search. The result for \(\textsf{MGL}^\circ \) follows from the fact that it satisfies the quasi-subformula property (i.e., every formula in the premise of a rule is a quasi-subformula a formula in its conclusion), and that
and \(\mathop \otimes \) can be introduced during proof search. The result for \(\textsf{MGL}^\circ \) follows from the fact that it satisfies the quasi-subformula property (i.e., every formula in the premise of a rule is a quasi-subformula a formula in its conclusion), and that
 and \(\mathop \otimes \) have no sub-connectives.
and \(\mathop \otimes \) have no sub-connectives.
For both \(\textsf{MGL}\) and \(\textsf{MGL}^\circ \) we have the following splitting result, ensuring that it is always possible, during proof search, to apply a rule removing a connective after having applied certain rules in the context. Note that, in the literature of linear logic, the splitting lemma is usually formulated as a special case of the next lemma, ensuring that an occurrence of the connective \(\mathop \otimes \) can be removed (by applying a \(\mathop \otimes \)-rule), but without requiring the possibility of the need of applying rules to the context.
Lemma 2
(Splitting). Let \(\varGamma , \kappa _{}\llparenthesis \phi _1, \ldots , \phi _n\rrparenthesis \) be a sequent and let \(\textsf{X}_{}\in \{\textsf{MGL},\textsf{MGL}^\circ \}\). If \(\mathord {\vdash _{\textsf{X}_{}}\,}\varGamma ,\kappa _{}\llparenthesis \phi _1, \ldots , \phi _n\rrparenthesis \), then there is a derivation of the following shape

Proof
By case analysis of the last rule occurring in a proof \(\pi \) of \(\varGamma , \kappa _{}\llparenthesis \phi _1, \ldots , \phi _n\rrparenthesis \).
We conclude this section by proving the admissibility of rules
 and \(\textsf{deep}\).
and \(\textsf{deep}\).
Lemma 3
The rule
 is admissible in \(\textsf{MGL}^\circ \).
is admissible in \(\textsf{MGL}^\circ \).
Proof
In Fig. 6 we provide a procedure to remove (top-down) all occurrences of
 . Similar to cut-elimination, this procedure requires the use the commutative steps to ensure that the active formula of a
. Similar to cut-elimination, this procedure requires the use the commutative steps to ensure that the active formula of a
 we aim at removing is principal with respect to the rule immediately above it.
we aim at removing is principal with respect to the rule immediately above it.
Lemma 4
The rule \(\textsf{deep}\) is admissible in \(\textsf{MGL}^\circ \).
Proof
By induction on the structure of \(\zeta [\Box ]\). The case with \(\zeta [\Box ]=\Box \) is an application of \(\textsf{wd}_{\mathop \otimes }\), otherwise we conclude using Lemma 2.
3.2 A Decomposition Result for \(\textsf{KGL}\)
We can extend the decomposition result for deep inference systems in the context of classical logic [13, 15] to \(\textsf{KGL}\) using the deep inference (structural) rules from Fig. 7, including the generalized medial rule proposed in [17].
Theorem 6
(Decomposition). Let \(\varGamma \) be a sequent. If \(\mathord {\vdash _{\textsf{KGL}}\,}\varGamma \), then:
-
1.
there is a sequent \(\varGamma '\) such that \(\mathord {\vdash _{\textsf{MGL}}\,}\varGamma ' \mathord {\vdash _{\{\mathsf w\mathord {\downarrow },\mathsf c\mathord {\downarrow }\}}\,}\varGamma \)
-
2.
there are sequent \(\varGamma '\), \(\varDelta '\), and \(\varDelta \) such that \(\mathord {\vdash _{\textsf{MGL}}\,}\varGamma ' \mathord {\vdash _{\{\mathsf m\}}\,}\varDelta ' \mathord {\vdash _{\{\textsf{ac}\mathord {\downarrow }\}}\,}\varDelta \mathord {\vdash _{\{\mathsf w\mathord {\downarrow }\}}\,}\varGamma \)
Proof
The proof of Item 1 is immediate by replacing structural rules with deep ones, and applying rule permutations. Item 2 is a consequence of the previous point after showing (by induction) that each instance of \(\mathsf c\mathord {\downarrow }\)-rule can be replaced by a derivation containing \(\mathsf m\) and \(\textsf{ac}\mathord {\downarrow }\) only, and conclude by applying rule permutations to push \(\textsf{ac}\)-rules below \(\mathsf m\)-rules, and \(\mathsf w\mathord {\downarrow }\) to the bottom of a derivation. For a reference, see [7].
4 Graph Isomorphism as Logical Equivalence
In this section we show that two pure formulas \(\phi \) and \(\psi \) are interpreted by the same graph (i.e., \(\left[ \!\left[ \phi \right] \!\right] =\left[ \!\left[ \psi \right] \!\right] \)) iff they are logically equivalent (i.e.,
 ).
).
Theorem 7
Let \(\phi \) and \(\psi \) be formulas.
-
1.
If \(\phi \) and \(\psi \) are unit-free, then \(\left[ \!\left[ \phi \right] \!\right] =\left[ \!\left[ \psi \right] \!\right] \) iff
 .
. -
2.
If \(\phi \) and \(\psi \) are pure, then \(\left[ \!\left[ \phi \right] \!\right] =\left[ \!\left[ \psi \right] \!\right] \) iff
 .
.
Proof
After Proposition 2, to prove Item 1 it suffices to show that each De Morgan law \(\phi \equiv \psi \) in Definition 12 (with \(\phi \) and \(\psi \) unit-free) corresponds to a logical equivalence
 which is derivable in \(\textsf{MGL}\). We then conclude by Corollary 3. To prove Item 2, we first show that we can find unit-free formulas \(\phi '\) and \(\psi '\) such that
which is derivable in \(\textsf{MGL}\). We then conclude by Corollary 3. To prove Item 2, we first show that we can find unit-free formulas \(\phi '\) and \(\psi '\) such that
 and
and
 are derivable in \(\textsf{MGL}^\circ \) (using \(\textsf{AX}\), \(\textsf {d}-\kappa _{}\), and \(\textsf{u}_{\kappa _{}}\) only), and we then conclude using the previous point.
are derivable in \(\textsf{MGL}^\circ \) (using \(\textsf{AX}\), \(\textsf {d}-\kappa _{}\), and \(\textsf{u}_{\kappa _{}}\) only), and we then conclude using the previous point.
5 Soundness and Completeness of \(\textsf{MGL}^\circ \) with Respect to \(\textsf{GS}\)
In this section, we show that the graphical logic \(\textsf{GS}\) from [4, 5], defined by a deep inference system operating on graphs, is the set of graphs corresponding to formulas that are provable in \(\textsf{MGL}^\circ \). Note that we here consider the system
 defined by the rules in Fig. 8, which have a slightly different formulation with respect to [4, 5]: we consider \(\textsf{p}\)-rules with a stronger side condition which is balanced by the presence of \(\textsf{s}_{\mathop \otimes }\) in the system.Footnote 4
defined by the rules in Fig. 8, which have a slightly different formulation with respect to [4, 5]: we consider \(\textsf{p}\)-rules with a stronger side condition which is balanced by the presence of \(\textsf{s}_{\mathop \otimes }\) in the system.Footnote 4
To prove the main result of this section, we use the admissibility of
 and \(\textsf{deep}\) (Lemmas 3 and 4) to prove that if \(H\) and \(G\) are graphs such that there is an application of a rule
and \(\textsf{deep}\) (Lemmas 3 and 4) to prove that if \(H\) and \(G\) are graphs such that there is an application of a rule
 , \(\textsf{s}_{\mathop \otimes }\), or \(\textsf{p}\mathord {\downarrow }\) (even deep in a context) with premise \(H\) and conclusion \(G\), then there are formulas \(\phi \) and \(\psi \), with \(\left[ \!\left[ \phi \right] \!\right] =H\) and \(\left[ \!\left[ \psi \right] \!\right] =G\), such that \(\psi \multimap \phi \).
, \(\textsf{s}_{\mathop \otimes }\), or \(\textsf{p}\mathord {\downarrow }\) (even deep in a context) with premise \(H\) and conclusion \(G\), then there are formulas \(\phi \) and \(\psi \), with \(\left[ \!\left[ \phi \right] \!\right] =H\) and \(\left[ \!\left[ \psi \right] \!\right] =G\), such that \(\psi \multimap \phi \).
Lemma 5
Let
 . If
. If
 , then there are formulas \(\phi \) and \(\psi \) with \(\left[ \!\left[ \phi \right] \!\right] ={G}\) and \(\left[ \!\left[ \psi \right] \!\right] ={H}\) such that \(\mathord {\vdash _{\textsf{MGL}^\circ }\,}\psi ^\bot , \phi \).
, then there are formulas \(\phi \) and \(\psi \) with \(\left[ \!\left[ \phi \right] \!\right] ={G}\) and \(\left[ \!\left[ \psi \right] \!\right] ={H}\) such that \(\mathord {\vdash _{\textsf{MGL}^\circ }\,}\psi ^\bot , \phi \).
Proof
If \(\mathcal {C}[\Box ]=\Box \), then the following implications trivially hold in \(\textsf{MGL}^\circ \):

If \(\mathcal {C}[\Box ]=\kappa _{P}\llparenthesis \mathcal {C}'[\Box ], M_1, \ldots , M_n\rrparenthesis \ne \Box \), then we assume w.l.o.g., there is a context formula \(\zeta [\Box ]=\kappa _{P}\llparenthesis \zeta '[\Box ], \mu _1, \ldots , \mu _n\rrparenthesis \) such that \(\left[ \!\left[ \zeta [\Box ] \right] \!\right] =\mathcal {C}[\Box ]\) and \(\left[ \!\left[ \zeta '[\Box ] \right] \!\right] =\mathcal {C}'[\Box ]\) . We conclude since, by inductive hypothesis on \(\mathcal {C}[\Box ]\), there is a derivation as follows:

We are now able to prove the main result of this section, that is, establishing a correspondence between graphs provable in \(\textsf{GS}\) and graphs which are the image via \(\left[ \!\left[ \cdot \right] \!\right] \) of formulas provable in \(\textsf{MGL}^\circ \).
Theorem 8
Let \(\phi \) a pure formula and let \(G=\left[ \!\left[ \phi \right] \!\right] \ne \varnothing \). Then \(\mathord {\vdash _{\textsf{GS}}\,}G\) iff \(\mathord {\vdash _{\textsf{MGL}^\circ }\,}\phi \).
Proof
If there is a derivation \(\pi \) of \(\varGamma \) in \(\textsf{MGL}^\circ \), then we define a derivation \(\left[ \!\left[ \pi \right] \!\right] \) of \(\left[ \!\left[ \varGamma \right] \!\right] \) in \(\textsf{GS}\) by induction by induction on the last rule \(\textsf{r}\) in \(\pi \). The translation translates a \(\textsf{ax}\) into an instance of \(\textsf{ai}\mathord {\downarrow }\), a
 , \(\textsf{mix}\) and \(\textsf{u}_{\kappa _{}}\) into no rule (using properties of the open deduction formalism, and the fact premise and conclusion sequents correspond to the same graph), \(\mathop \otimes \) and \(\textsf {d}-\kappa _{}\) into an instance of \(\textsf{p}\mathord {\downarrow }\), and \(\textsf{wd}_{\mathop \otimes }\) into an instance of \(\textsf{p}\mathord {\downarrow }\).
, \(\textsf{mix}\) and \(\textsf{u}_{\kappa _{}}\) into no rule (using properties of the open deduction formalism, and the fact premise and conclusion sequents correspond to the same graph), \(\mathop \otimes \) and \(\textsf {d}-\kappa _{}\) into an instance of \(\textsf{p}\mathord {\downarrow }\), and \(\textsf{wd}_{\mathop \otimes }\) into an instance of \(\textsf{p}\mathord {\downarrow }\).
Conversely, if \(\mathcal {D}\) is a proof of \(G\ne \varnothing \) in \(\textsf{GS}\), then we define a proof \(\pi _\mathcal {D}\) of \(\phi \) by induction on the number n of rules in \(\mathcal {D}\), where \(n\ne 0\) because we are assuming \(G\ne \varnothing \).
-
If \(n=1\), then
 and
and
 .
. -
If \(n>1\), then the derivation \(\mathcal {D}\) is of the form
 and by inductive hypothesis we have a proof \(\pi _{\mathcal {D}'}\) of a formula \(\psi \) such that \(\left[ \!\left[ \psi \right] \!\right] =H\). If
and by inductive hypothesis we have a proof \(\pi _{\mathcal {D}'}\) of a formula \(\psi \) such that \(\left[ \!\left[ \psi \right] \!\right] =H\). If
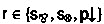 , then by Lemma 5 we have a derivation with \(\textsf{cut}\) as the one below on the left of a formula \(\phi \) such that \(\left[ \!\left[ \phi \right] \!\right] =G\). Thus we conclude by Theorem 5.
, then by Lemma 5 we have a derivation with \(\textsf{cut}\) as the one below on the left of a formula \(\phi \) such that \(\left[ \!\left[ \phi \right] \!\right] =G\). Thus we conclude by Theorem 5. 
Otherwise \(\textsf{r}=\textsf{ai}\mathord {\downarrow }\), then it must have been applied deep inside a context \(\mathcal {C}[\Box ]=\left[ \!\left[ \zeta [\Box ] \right] \!\right] \ne \Box \) such that \(\mathcal {C}[\varnothing ]=H=\left[ \!\left[ \psi \right] \!\right] \). Therefore
 . We conclude by applying Lemma 4 to the derivation above on the right.
. We conclude by applying Lemma 4 to the derivation above on the right.
Remark 6
In a different line of work [17] the authors define the boolean graphical logic (or \(\textsf{GBL}\)), as a graphical logic conservatively extending \(\textsf{LK}\) defined by maximal-clique-preserving graph morphisms. As a consequence of Corollary 4 and theorem 8, we conclude that \(\textsf{KGL}\) and \(\textsf{GBL}\) are not the same since the following counterexample from [5] (for \(\textsf{GS}\)) is in \(\textsf{GBL}\) but not in \(\textsf{KGL}\)
 .
.
6 Conclusion and Future Works
In this paper we have provided foundations for the design of proof systems operating on graphs by defining graphical connectives, a class of logical operators generalizing the classical conjunction and disjunction, and whose semantics is solely defined by their interpretation as prime graphs. We introduced cut-free sequent calculi operating on formulas containing graphical connectives, where graph isomorphism can be captured by logical equivalence. We also discussed the relationship of these systems with graphical logics studied in the literature [4, 5, 17].
We illustrate below a number of future research directions originating from this work different from the suggestions of the respective authors of using the graphical logic \(\textsf{GS}\) to extend the works in [11, 18, 49], where the authors suggest the possibility of extending their current results by generalizing their methods based on “classical” formulas to graphs.
Categorical Semantics. Unit-free star-autonomous and IsoMix categories [19, 20] provide categorical models of \(\textsf{MLL}\) and \(\textsf{MLL}^{\circ }\) respectively. We conjecture that categorical models for \(\textsf{MGL}\) and \(\textsf{MGL}^\circ \) can be defined by enriching such structures with additional n-ary monoidal products and natural transformations, reflecting the symmetries observed in the symmetry groups of prime graphs.
Digraphs, Games and Event Structures. In this work we have extended the correspondence between classical propositional and cographs from [21] to the case of general (undirected) graphs using graphical connectives, and the same idea can be found in [3] where mixed graphs generalize relation webs used to encode \(\textsf{BV}\)-formulas [33]. Similarly, we foresee the definition of proof systems operating on directed graphs as conservative extensions of intuitionistic propositional logic beyond arenas – directed graphs used in Hyland-Ong game semantics [40] to encode propositional intuitionistic formulas, which are characterized by the absence of induced subgraphs of a specific shape. This would provide new insights on the proof theory connected to concurrent games [1, 58, 64], and could be used to define automated tools operating on event structures [55].
On the left: the same proof net in the original Girard’s syntax and Retoré’s one. On the right: an RB-proof net of \(\kappa _{\mathsf {P_4}}\llparenthesis a,b,c,d\rrparenthesis \multimap \kappa _{\mathsf {P_4}}\llparenthesis a,b,c,d\rrparenthesis \) containing the chorded æ-cycle \(a\cdot b \cdot b^\bot \cdot d^\bot \cdot d \cdot c \cdot c^\bot \cdot a^\bot \).
Proof Nets and Automated Proof Search. We plan to design proof nets [22, 29, 30] for \(\textsf{MGL}\) and \(\textsf{MGL}^\circ \), as well as combinatorial proofs [38, 39] for \(\textsf{KGL}\). For this purpose, we envisage extending Retoré’s handsome proof net syntax, where proof nets are represented by two-colored graphs (see the left of Fig. 9). In Retoré’s syntax, the graph induced by the vertices corresponding to the inputs of a
 -gate (or a \(\mathop \otimes \)-gate) is similar to the corresponding prime graph
-gate (or a \(\mathop \otimes \)-gate) is similar to the corresponding prime graph
 (resp. \(\mathop \otimes \)). Thus, gates for graphical connectives could be easily defined by extending this correspondence (see the proof net on the right of Fig. 9). The standard correctness condition defined via acyclicity fails for these proof nets, as shown in the right-hand side of Fig. 9: the (correct) proof-net of the sequent \(\mathsf {P_4}\llparenthesis a,b,c,d\rrparenthesis \multimap \mathsf {P_4}\llparenthesis a,b,c,d\rrparenthesis \) contains a cycle. We foresee the possibility of using results on the primeval decomposition of graphs [37, 42] to isolate those cycles witnessing unsoundness, as proposed in [52]. This may provide a methodology to develop machine-learning guided automated theorem provers using the methods in [43].
(resp. \(\mathop \otimes \)). Thus, gates for graphical connectives could be easily defined by extending this correspondence (see the proof net on the right of Fig. 9). The standard correctness condition defined via acyclicity fails for these proof nets, as shown in the right-hand side of Fig. 9: the (correct) proof-net of the sequent \(\mathsf {P_4}\llparenthesis a,b,c,d\rrparenthesis \multimap \mathsf {P_4}\llparenthesis a,b,c,d\rrparenthesis \) contains a cycle. We foresee the possibility of using results on the primeval decomposition of graphs [37, 42] to isolate those cycles witnessing unsoundness, as proposed in [52]. This may provide a methodology to develop machine-learning guided automated theorem provers using the methods in [43].
Notes
- 1.
A similar approach was proposed in [56] for studying pomsets.
- 2.
It can be easily shown that \(\mathfrak {S}_{n}\) contains the identity permutation (denoted \(\textsf{id}\)) and is a subgroup of the group of permutations over the set \(\{1,\ldots ,n\}\).
- 3.
Note that the permutation \(\sigma \) may be not unique. If we consider formulas up-to the equivalence relation \(\equiv \), this is irrelevant. Otherwise, in the definition of the linear negation we should also provide a specific permutation \(\sigma _P\) for each prime connective \(P\in \mathcal {P}\).
- 4.
References
Abramsky, S., Mellies, P.A.: Concurrent games and full completeness. In: Proceedings. 14th Symposium on Logic in Computer Science (Cat. No. PR00158), pp. 431–442. IEEE (1999)
Acclavio, M.: Graphical proof theory I: sequent systems on undirected graphs (2023)
Acclavio, M., Horne, R., Mauw, S., Straßburger, L.: A graphical proof theory of logical time. In: Felty, A.P. (ed.) 7th International Conference on Formal Structures for Computation and Deduction (FSCD 2022). Leibniz International Proceedings in Informatics (LIPIcs), vol. 228, pp. 22:1–22:25. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, Dagstuhl, Germany (2022). https://doi.org/10.4230/LIPIcs.FSCD.2022.22, https://drops.dagstuhl.de/opus/volltexte/2022/16303
Acclavio, M., Horne, R., Straßburger, L.: Logic beyond formulas: a proof system on graphs. In: Proceedings of the 35th Annual ACM/IEEE Symposium on Logic in Computer Science. LICS ’20, pp. 38–52. Association for Computing Machinery, New York, NY, USA (2020). https://doi.org/10.1145/3373718.3394763
Acclavio, M., Horne, R., Straßburger, L.: An analytic propositional proof system on graphs. Logical Methods Comput. Sci. 18(4) (2022). https://doi.org/10.46298/lmcs-18(4:1)2022, https://lmcs.episciences.org/10186
Acclavio, M., Maieli, R.: Generalized connectives for multiplicative linear logic. In: Fernández, M., Muscholl, A. (eds.) 28th EACSL Annual Conference on Computer Science Logic (CSL 2020). LIPIcs, vol. 152, pp. 6:1–6:16. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, Dagstuhl, Germany (2020). https://doi.org/10.4230/LIPIcs.CSL.2020.6, https://drops.dagstuhl.de/opus/volltexte/2020/11649
Acclavio, M., Straßburger, L.: From syntactic proofs to combinatorial proofs. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS (LNAI), vol. 10900, pp. 481–497. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_32
Aler Tubella, A., Straßburger, L.: Introduction to Deep Inference, August 2019. https://hal.inria.fr/hal-02390267, lecture
Andreoli, J.M.: Logic programming with focusing proofs in linear logic. J. Log. Comput. 2(3), 297–347 (1992)
Avron, A., Lev, I.: Canonical propositional Gentzen-type systems. In: Goré, R., Leitsch, A., Nipkow, T. (eds.) IJCAR 2001. LNCS, vol. 2083, pp. 529–544. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45744-5_45
Bellandi, V., Frati, F., Siccardi, S., Zuccotti, F.: Management of uncertain data in event graphs. In: Ciucci, D., et al. (eds.) IPMU 2022. CCIS, vol. 1601, pp. 568–580. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-08971-8_47
Blackburn, P., De Rijke, M., Venema, Y.: Modal logic: graph. Darst, vol. 53. Cambridge University Press (2001)
Brünnler, K.: Locality for classical logic. Notre Dame J. Formal Logic 47(4), 557–580 (2006). http://www.iam.unibe.ch/~kai/Papers/LocalityClassical.pdf
Brünnler, K., Straßburger, L.: Modular sequent systems for modal logic. In: Giese, M., Waaler, A. (eds.) TABLEAUX 2009. LNCS (LNAI), vol. 5607, pp. 152–166. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02716-1_12
Bruscoli, P., Straßburger, L.: On the length of medial-switch-mix derivations. In: Kennedy, J., de Queiroz, R.J.G.B. (eds.) WoLLIC 2017. LNCS, vol. 10388, pp. 68–79. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-55386-2_5
Calk, C.: A graph theoretical extension of Boolean logic. Bachelor’s thesis (2016). http://www.anupamdas.com/graph-bool.pdf
Calk, C., Das, A., Waring, T.: Beyond formulas-as-cographs: an extension of Boolean logic to arbitrary graphs (2020)
Chaudhuri, K., Donato, P., Massacci, L., Werner, B.: Certifying proof-by-linking. In: Working Paper or Preprint, September 2022. https://inria.hal.science/hal-04317972
Cockett, J., Seely, R.: Proof theory for full intuitionistic linear logic, bilinear logic, and mix categories. Theory Appl. Categories 3(5), 85–131 (1997)
Cockett, J., Seely, R.: Weakly distributive categories. J. Pure Appl. Algebra 114, 133–173 (1997)
Corneil, D., Lerchs, H., Burlingham, L.: Complement reducible graphs. Discrete Appl. Math. 3(3), 163–174 (1981). https://doi.org/10.1016/0166-218X(81)90013-5, https://www.sciencedirect.com/science/article/pii/0166218X81900135
Danos, V., Regnier, L.: The structure of multiplicatives. Arch. Math. Logic 28(3), 181–203 (1989). https://doi.org/10.1007/BF01622878
Das, A.: Complexity of evaluation and entailment in Boolean graph logic (2019, preprint). http://www.anupamdas.com/complexity-graph-bool-note.pdf
Das, A., Rice, A.A.: New minimal linear inferences in Boolean logic independent of switch and medial. In: Kobayashi, N. (ed.) 6th International Conference on Formal Structures for Computation and Deduction. FSCD 2021, 17–24 July 2021, Buenos Aires, Argentina (Virtual Conference). LIPIcs, vol. 195, pp. 14:1–14:19. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2021). https://doi.org/10.4230/LIPIcs.FSCD.2021.14
Deniélou, P.-M., Yoshida, N.: Buffered communication analysis in distributed multiparty sessions. In: Gastin, P., Laroussinie, F. (eds.) CONCUR 2010. LNCS, vol. 6269, pp. 343–357. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15375-4_24
Ehrenfeucht, A., Harju, T., Rozenberg, G.: The Theory of 2-Structures a Framework for Decomposition and Transformation of Graphs. World Scientific, Singapore (1999). https://doi.org/10.1142/4197
Fu, X., Bultan, T., Su, J.: Analysis of interacting BPEL web services. In: Proceedings of the 13th International Conference on World Wide Web, pp. 621–630. ACM (2004)
Gallai, T.: Transitiv orientierbare Graphen. Acta Mathematica Academiae Scientiarum Hungarica 18(1–2), 25–66 (1967)
Girard, J.Y.: Linear logic. Theor. Comput. Sci. 50, 1–102 (1987). https://doi.org/10.1016/0304-3975(87)90045-4
Girard, J.Y.: Proof-nets: the parallel syntax for proof-theory. In: Ursini, A., Agliano, P. (eds.) Logic and Algebra. Marcel Dekker, New York (1996)
Girard, J.Y.: Light linear logic. Inf. Comput. 143, 175–204 (1998)
Girard, J.Y.: On the meaning of logical rules II: multiplicatives and additives. NATO ASI Seri. F: Comput. Syst. Sci. 175, 183–212 (2000)
Guglielmi, A.: A system of interaction and structure. ACM Trans. Comput. Log. 8(1), 1–64 (2007). https://doi.org/10.1145/1182613.1182614
Guglielmi, A., Gundersen, T., Parigot, M.: A proof calculus which reduces syntactic bureaucracy. In: Lynch, C. (ed.) Proceedings of the 21st International Conference on Rewriting Techniques and Applications. LIPIcs, vol. 6, pp. 135–150. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, Dagstuhl, Germany (2010). https://doi.org/10.4230/LIPIcs.RTA.2010.135, http://drops.dagstuhl.de/opus/volltexte/2010/2649
Habib, M., Paul, C.: A survey of the algorithmic aspects of modular decomposition. Comput. Sci. Rev. 4(1), 41–59 (2010). https://doi.org/10.1016/j.cosrev.2010.01.001, https://www.sciencedirect.com/science/article/pii/S157401371000002X
van Heerdt, G., Kappé, T., Rot, J., Silva, A.: Learning Pomset Automata. In: FOSSACS 2021. LNCS, vol. 12650, pp. 510–530. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-71995-1_26
Hougardy, S.: On the P4-structure of perfect graphs. Citeseer (1996)
Hughes, D.: Proofs without syntax. Ann. Math. 164(3), 1065–1076 (2006). https://doi.org/10.4007/annals.2006.164.1065
Hughes, D.: Towards Hilbert’s 24\({}^{\text{ th }}\) problem: combinatorial proof invariants: (preliminary version). Electr. Notes Theor. Comput. Sci. 165, 37–63 (2006)
Hyland, J.M.E., Ong, C.H.L.: On full abstraction for PCF: I. Models, observables and the full abstraction problem, II. Dialogue games and innocent strategies, III. A fully abstract and universal game model. Inf. Comput. 163, 285–408 (2000)
James, L.O., Stanton, R.G., Cowan, D.D.: Graph decomposition for undirected graphs. In: Proceedings of the Third Southeastern Conference on Combinatorics, Graph Theory, and Computing (Florida Atlantic Univ., Boca Raton, Fla., 1972). pp. 281–290 (1972)
Jamison, B., Olariu, S.: P-components and the homogeneous decomposition of graphs. SIAM J. Discret. Math. 8(3), 448–463 (1995)
Kogkalidis, K., Moortgat, M., Moot, R.: Neural proof nets. In: Fernández, R., Linzen, T. (eds.) Proceedings of the 24th Conference on Computational Natural Language Learning, pp. 26–40. Association for Computational Linguistics, Online (2020). https://doi.org/10.18653/v1/2020.conll-1.3, https://aclanthology.org/2020.conll-1.3
Lellmann, B., Pimentel, E.: Modularisation of sequent calculi for normal and non-normal modalities. ACM Trans. Comput. Logic 20(2) (2019). https://doi.org/10.1145/3288757
Lovász, L., Plummer, M.D.: Matching Theory, vol. 367. American Mathematical Society, Providence (2009)
Mac Lane, S.: Categories for the Working Mathematician. Graduate Texts in Mathematics, vol. 5. Springer, New York (1971). https://doi.org/10.1007/978-1-4757-4721-8
Maieli, R.: Non decomposable connectives of linear logic. Ann. Pure Appl. Logic 170(11), 102709 (2019). https://doi.org/10.1016/j.apal.2019.05.006, http://www.sciencedirect.com/science/article/pii/S0168007219300600
McConnell, R.M., Spinrad, J.P.: Linear-time modular decomposition and efficient transitive orientation of comparability graphs. In: Proceedings of the Fifth Annual ACM-SIAM Symposium on Discrete Algorithms. SODA ’94, pp. 536–545. Society for Industrial and Applied Mathematics, USA (1994)
Mell, S., Bastani, O., Zdancewic, S.: Ideograph: a language for expressing and manipulating structured data. In: Grabmayer, C. (ed.) Proceedings Twelfth International Workshop on Computing with Terms and Graphs, TERMGRAPH@FSCD 2022, Technion, Haifa, Israel, 1st August 2022. EPTCS, vol. 377, pp. 65–84 (2022). https://doi.org/10.4204/EPTCS.377.4
Miller, D., Pimentel, E.: A formal framework for specifying sequent calculus proof systems. Theor. Comput. Sci. 474, 98–116 (2013)
Miller, D., Saurin, A.: From proofs to focused proofs: a modular proof of focalization in linear logic. In: Duparc, J., Henzinger, T.A. (eds.) CSL 2007. LNCS, vol. 4646, pp. 405–419. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74915-8_31
Nguyên, L.T.D., Seiller, T.: Coherent interaction graphs: a non-deterministic geometry of interaction for MLL (2019)
Nguyên, L.T.D., Straßburger, L.: A system of interaction and structure III: the complexity of BV and Pomset logic. In: Working Paper or Preprint (2022). https://hal.inria.fr/hal-03909547
Nguyên, L.T.D., Straßburger, L.: BV and Pomset logic are not the same. In: Manea, F., Simpson, A. (eds.) 30th EACSL Annual Conference on Computer Science Logic (CSL 2022). Leibniz International Proceedings in Informatics (LIPIcs), vol. 216, pp. 3:1–3:17. Schloss Dagstuhl – Leibniz-Zentrum für Informatik, Dagstuhl, Germany (2022). https://doi.org/10.4230/LIPIcs.CSL.2022.3, https://drops.dagstuhl.de/opus/volltexte/2022/15723
Nielsen, M., Plotkin, G., Winskel, G.: Petri nets, event structures and domains, part I. Theor. Comput. Sci. 13(1), 85–108 (1981)
Pratt, V.: Modeling concurrency with partial orders. Int. J. Parallel Prog. 15, 33–71 (1986)
Retoré, C.: Pomset logic: the other approach to noncommutativity in logic. In: Joachim Lambek: The Interplay of Mathematics, Logic, and Linguistics, pp. 299–345 (2021)
Rideau, S., Winskel, G.: Concurrent strategies. In: 2011 IEEE 26th Annual Symposium on Logic in Computer Science, pp. 409–418. IEEE (2011)
Seely, R.: Linear logic, *-autonomous categories and cofree coalgebras. Contemp. Math. 92 (1989)
Tiu, A.F.: A system of interaction and structure II: the need for deep inference. Logic. Methods Comput. Sci. 2(2), 1–24 (2006). https://doi.org/10.2168/LMCS-2(2:4)2006
Troelstra, A.S., Schwichtenberg, H.: Basic Proof Theory, 2nd edn. Cambridge University Press, Cambridge (2000)
Valdes, J., Tarjan, R.E., Lawler, E.L.: The recognition of series parallel digraphs. In: Proceedings of the Eleventh Annual ACM Symposium on Theory of Computing, pp. 1–12. ACM (1979)
Waring, T.: A graph theoretic extension of Boolean logic. Master’s thesis (2019). http://anupamdas.com/thesis_tim-waring.pdf
Winskel, G., Rideau, S., Clairambault, P., Castellan, S.: Games and strategies as event structures. Logic. Methods Comput. Sci. 13 (2017)
Acknowledgments
The author thanks the anonymous reviewers for the feedback which helped improve the final version of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Acclavio, M. (2024). Sequent Systems on Undirected Graphs. In: Benzmüller, C., Heule, M.J., Schmidt, R.A. (eds) Automated Reasoning. IJCAR 2024. Lecture Notes in Computer Science(), vol 14740. Springer, Cham. https://doi.org/10.1007/978-3-031-63501-4_12
Download citation
DOI: https://doi.org/10.1007/978-3-031-63501-4_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-63500-7
Online ISBN: 978-3-031-63501-4
eBook Packages: Computer ScienceComputer Science (R0)












 rules.
rules.
 .
. .
.
 and
and
 .
. and by inductive hypothesis we have a proof
and by inductive hypothesis we have a proof 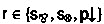 , then by Lemma
, then by Lemma 
 . We conclude by applying Lemma
. We conclude by applying Lemma 
 (as in [
(as in [