Abstract
This paper connects the following three apparently unrelated topics: an epistemic framework fighting logical omniscience, a class of generalized graphs without the arities of relations, and a family of non-normal modal logics rejecting the aggregative axiom. Through neighborhood frames as their meeting point, we show that, among many completeness results obtained in this paper, the limit of a family of weakly aggregative logics is both exactly the modal logic of hypergraphs and also the epistemic logic of local reasoning with veracity and positive introspection. The logics studied are shown to be decidable based on a filtration construction.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
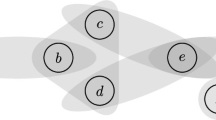
The graph is a variant of an example in [3], where hypergrphs are used to represent semi-public broadcasting channels for interacting agents.
References
Apostoli, P.: Modal aggregation and the theory of paraconsistent filters. Math. Logic Q. 42(1), 175–190 (1996)
Apostoli, P., Brown, B.: A solution to the completeness problem for weakly aggregative modal logic. J. Symbol. Logic 60(3), 832–842 (1995)
Apt, K.R., Witzel, A., Zvesper, J.A.: Common knowledge in interaction structures. In: Proceedings of TARK 2009, pp. 4–13. Association for Computing Machinery, New York (2009)
Baltag, A., Bezhanishvili, N., Özgün, A., Smets, S.: Justified belief and the topology of evidence. In: Väänänen, J., Hirvonen, Å., de Queiroz, R. (eds.) WoLLIC 2016. LNCS, vol. 9803, pp. 83–103. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-52921-8_6
van Benthem, J., Fernández-Duque, D., Pacuit, E.: Evidence and plausibility in neighborhood structures. Ann. Pure Appl. Logic 165(1), 106–133 (2014)
Berge, C.: Hypergraphs: Combinatorics of Finite Sets, vol. 45. Elsevier (1984)
Chellas, B.F.: Modal Logic: An Introduction. Cambridge University Press, Cambridge (1980)
Dabrowski, A., Moss, L.S., Parikh, R.: Topological reasoning and the logic of knowledge. Ann. Pure Appl. Logic 78(1–3), 73–110 (1996)
Fagin, R., Halpern, J.Y.: Belief, awareness, and limited reasoning. Artif. Intell. 34(1), 39–76 (1988)
Gu, T., Wang, Y.: “knowing value” logic as a normal modal logic. In: Proceedings of AiML, vol. 11, pp. 362–381 (2016)
Hansen, H.H.: Monotonic modal logics. Master’s thesis, Institute for Logic, Language and Computation (ILLC), University of Amsterdam (2003)
Liu, J., Wang, Y., Ding, Y.: Weakly aggregative modal logic: characterization and interpolation. In: Blackburn, P., Lorini, E., Guo, M. (eds.) LORI 2019. LNCS, vol. 11813, pp. 153–167. Springer, Heidelberg (2019). https://doi.org/10.1007/978-3-662-60292-8_12
Nicholson, D.: A dualization of neighbourhood structures. In: Jennings, R.E., Schotch, P.K., Brown, B. (eds.) On Preserving: Essays on Preservationism and Paraconsistent Logic, pp. 49–60. University of Toronto Press (2009)
Nicholson, T., Jennings, R.E., Sarenac, D.: Revisiting completeness for the \({K}_{n}\) modal logics: a new proof. Logic J. IGPL 8(1), 101–105 (2000)
Pacuit, E.: Neighborhood Semantics for Modal Logic. Springer, Cham (2017)
Schotch, P., Jennings, R.: Modal logic and the theory of modal aggregation. Philosophia 9(2), 265–278 (1980)
Urquhart, A.: Weakly additive algebras and a completeness problem. In: Jennings, R.E., Schotch, P.K., Brown, B. (eds.) On Preserving: Essays on Preservationism and Paraconsistent Logic, pp. 33–48. University of Toronto Press (2009)
Yamamoto, K.: Correspondence, canonicity, and model theory for monotonic modal logics. Studia Logica 109(2), 397–421 (2021)
Acknowledgment
The authors thank the anonymous reviewers for pointing out some related work. Jixin Liu thanks China Postdoctoral Science Foundation (2020M683344) for support. Yanjing Wang gratefully acknowledges the support from NSSF (grant 19BZX135).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Ding, Y., Liu, J., Wang, Y. (2021). Hypergraphs, Local Reasoning, and Weakly Aggregative Modal Logic. In: Ghosh, S., Icard, T. (eds) Logic, Rationality, and Interaction. LORI 2021. Lecture Notes in Computer Science(), vol 13039. Springer, Cham. https://doi.org/10.1007/978-3-030-88708-7_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-88708-7_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-88707-0
Online ISBN: 978-3-030-88708-7
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)