Abstract
Causal consistent reversibility blends causality and reversibility. For a concurrent system, it says that an action can be undone provided this has no consequences, thereby making it possible to bring the system back to a past consistent state. Time reversibility is considered instead in the performance evaluation field. A continuous-time Markov chain is time reversible if its behavior remains the same when the direction of time is reversed. We try to bridge these two theories by showing the conditions under which both causal consistent reversibility and time reversibility can be achieved in the setting of a stochastic process algebra.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The interest into computation reversibility dates back to the 60’s, when it was observed that irreversible computations cause heat dissipation into circuits [16]. This suggested that low energy consumption could be achieved by resorting to reversible computing, in which there is no information loss [3]. Nowadays, reversible computing has several applications ranging from biochemical reactions [29, 30] and parallel discrete-event simulation [27, 32] to robotics [22], control theory [33], fault tolerant systems [6, 17, 35, 36], and program debugging [7, 20].
In a reversible system, we can observe two directions of computation: a forward one, coinciding with the normal way of computing, and a backward one, which is able to undo the effects of the forward one. In the literature, there exist different meanings of reversibility. For instance, in a Petri net model reversibility means that one can always reach the initial marking [2], while in distributed systems it amounts to the capability of returning to a past consistent state [5]. In contrast, in the performance evaluation field, reversibility is intended as time reversibility and is instrumental to develop efficient analysis methods [13].
Our focus is on the relationship between causal consistent reversibility and time reversibility, from a process algebraic perspective. On the one hand, quantitative aspects have been disregarded in the setting of causal consistent reversibility. On the other hand, the theory of time reversibility has been applied to concurrent systems without explicitly taking causality into account.
In this paper, instead, we aim at bridging these two theories, by showing how causal consistent reversibility and time reversibility can be jointly obtained. To this purpose, we consider a stochastic process calculus in which every action is equipped with a positive real number expressing the rate at which the action is executed. As is well known in the literature [10], the stochastic process underlying the calculus turns out to be a continuous-time Markov chain (CTMC) [14].
The contribution of this paper is twofold. Firstly, we apply for the first time the technique of [28] to a stochastic process calculus. In particular, we provide forward and backward operational semantic rules – featuring forward and backward actions and rates – and then we show that the resulting calculus is causal consistent reversible. This is accomplished by importing from the reduction semantics setting of [5] the notion of concurrent transitions, which is new in the structural operational semantics framework of [28].
Secondly, after observing that the CTMC underlying the calculus is stationary, we show that time reversibility can be achieved by using, in the operational semantic rules, backward rates equal to the corresponding forward rates. This is quite different from the approaches followed for example in [8, 25], where time reversibility is addressed a posteriori, as we instead obtain a calculus in which time reversibility can be guaranteed by construction.
This paper is organized as follows. In Sects. 2 and 3 we recall background information about causal consistent reversibility and time reversibility, respectively. Then, in Sect. 4 we provide and illustrate our results about the integration of these two forms of reversibility in the considered stochastic process calculus. Finally, in Sect. 5 we conclude with some directions for future work.
2 Causal Consistent Reversibility
Reversibility in a system means the possibility of reverting the last performed action. In a sequential system, this is very simple as there exists just one last action. In a concurrent system, the situation is more complex as there is no clear definition of last action. Indeed, there might be several concurrent last actions. One could resort to timestamps to decide which action is the last one, but having synchronised clocks in a distributed system is rather difficult.
A good approximation is to consider as last action each action that has not caused any other action yet. This is at the basis of the so called causal consistent reversibility [5], which relates reversibility with causality. Intuitively, the definition says that, in a concurrent system, any action can be undone provided that all of its consequences, if any, are undone beforehand.
In the process algebra literature, there are two reversible variants of CCS [26]. The first one in time order, RCCS [5], uses stack-based memories attached to processes to record all the actions executed by the processes themselves. In contrast, [28] proposes a general method, of which CCSK is a result, to reverse calculi whose operational semantic rules are expressed in the path format [1]. The basic idea of this method is to make all the operators of the calculus static and to univocally identify each executed action with a communication key. Note that, since dynamic operators such as prefixing and choice are forgetful by definition, making them static avoids information loss during a reduction.
Despite these two approaches may seem different, they have been shown to be equivalent in terms of labeled transition system isomorphism [18]. The approach of [5] is more suitable for systems whose operational semantics is given in terms of reduction semantics, hence its application is to be preferred in the case of very expressive calculi [4, 19] as well as programming languages [21, 24]. On the other hand, the approach of [28] is very handy when it comes to deal with labeled transition systems and CCS-like calculi, which is the case of this paper.
For example, given the process \(P + Q\), from \(P \xrightarrow {\alpha } P'\) we derive \(P + Q \xrightarrow {\alpha } P'\). If we assume the possibility of reverting action \(\alpha \), i.e., \(P' \xrightarrow {\alpha _{\text {r}}} P\), we have that \(P'\) gets back to a state in which the information about the choice operator and Q is lost. To avoid this, in [28] \(+\, Q\) is treated as a dead decoration of process \(P'\). In this way, the use of explicit memories of [5] is avoided because the necessary information is syntactically maintained within processes.
3 Time Reversibility
In the field of performance evaluation, a different notion of reversibility, called time reversibility, is considered. We illustrate it in the specific case of continuous-time Markov chains, which are discrete-state stochastic processes characterized by the memoryless property [14].
A stochastic process describes the evolution of some random phenomenon over time through a set of random variables, one for each time instant. A stochastic process X(t) taking values into a discrete state space \(\mathcal {S}\) for \(t \in \mathbb {R}_{\ge 0}\) is a continuous-time Markov chain (CTMC) iff for all \(n \in \mathbb {N}\), time instants \(t_{0}< t_{1}< \dots< t_{n} < t_{n + 1} \in \mathbb {R}_{\ge 0}\), and states \(s_{0}, s_{1}, \dots , s_{n}, s_{n + 1} \in \mathcal {S}\) it holds that \(\Pr \{ X(t_{n + 1}) \! = \! s_{n + 1} \mid X(t_{i}) \! = \! s_{i}, 0 \le i \le n \} = \Pr \{ X(t_{n + 1}) \! = \! s_{n + 1} \mid X(t_{n}) \! = \! s_{n} \}\), i.e., the probability of moving from one state to another does not depend on the particular path that has been followed in the past to reach the current state, hence that path can be forgotten.
A CTMC is irreducible iff each of its states can be reached from every other state. A state \(s \in \mathcal {S}\) is recurrent iff the CTMC will eventually return to s with probability 1, in which case s is called positive recurrent iff the expected number of steps until the CTMC returns to it is finite. A CTMC is ergodic iff it is irreducible and all of its states are positive recurrent; ergodicity coincides with irreducibility in the case that the CTMC has finitely many states.
A CTMC can be represented as a labeled transition system or as a state-indexed matrix. In the first case, each transition is labeled with some probabilistic information describing the evolution from its source state to its target state. In the second case, the same information is stored into an entry, indexed by those two states, of a matrix. The value of this probabilistic information is, in general, a function of the time at which the state change takes place.
For the sake of simplicity, we restrict ourselves to time-homogeneous CTMCs, in which conditional probabilities of the form \(\Pr \{ X(t + t') = s' \mid X(t) = s \}\) do not depend on t, so that the considered information is simply a positive real number. This is called the rate at which the CTMC moves from state s to state \(s'\) and uniquely characterizes the exponentially distributed time taken by the considered move. It can be shown that the sojourn time in any state \(s \in \mathcal {S}\) is exponentially distributed with rate given by the sum of the rates of the moves of s. The average sojourn time in s is the inverse of such a sum and the probability of moving from s to \(s'\) is proportional to the corresponding rate.
Every time-homogeneous, ergodic CTMC X(t) is stationary, which means that \((X(t_{i} + t'))_{1 \le i \le n}\) has the same joint distribution as \((X(t_{i}))_{1 \le i \le n}\) for all \(n \in \mathbb {N}_{\ge 1}\) and \(t_{1}< \dots < t_{n}, t' \in \mathbb {R}_{\ge 0}\). Specifically, X(t) has a unique steady-state probability distribution \(\varvec{\pi }\) that for all \(s \in \mathcal {S}\) fulfills \(\pi (s) = \lim _{t \rightarrow \infty } \Pr \{ X(t) = s \mid X(0) = s' \}\) for any \(s' \in \mathcal {S}\). These probabilities can be computed by solving the linear system of global balance equations \(\varvec{\pi }\cdot \mathbf {Q} = \mathbf {0}\) subject to \(\sum _{s \in \mathcal {S}} \pi (s) = 1\) and \(\pi (s) \in \mathbb {R}_{> 0}\) for all \(s \in \mathcal {S}\). The infinitesimal generator matrix \(\mathbf {Q}\) contains for each pair of distinct states the rate of the corresponding move, which is 0 in the absence of a direct move between them, with \(q_{s, s} = - \sum _{s' \ne s} q_{s, s'}\) for all \(s \in \mathcal {S}\) so that every row of \(\mathbf {Q}\) sums up to 0.
Due to state space explosion and numerical stability problems [34], the calculation of the solution of the global balance equation system is not always feasible. However, it can be tackled in the case that the behavior of the considered CTMC remains the same when the direction of time is reversed. A CTMC X(t) is time reversible iff \((X(t_{i}))_{1 \le i \le n}\) has the same joint distribution as \((X(t' - t_{i}))_{1 \le i \le n}\) for all \(n \in \mathbb {N}_{\ge 1}\) and \(t_{1}< \dots < t_{n}, t' \in \mathbb {R}_{\ge 0}\), in which case X(t) and its reversed version \(X^{\text {r}}(t) = X(t' - t)\) are stochastically identical; in particular, X(t) and \(X^{\text {r}}(t)\) share the same steady-state probability distribution \(\varvec{\pi }\) if any. In order for a stationary CTMC X(t) to be time reversible, it is necessary and sufficient that the partial balance equations \(\pi (s) \cdot q_{s, s'} = \pi (s') \cdot q_{s', s}\) are satisfied for all \(s, s' \in \mathcal {S}\) such that \(s \ne s'\) or, equivalently, that \(q_{s_{1}, s_{2}} \cdot \ldots \cdot q_{s_{n - 1}, s_{n}} \cdot q_{s_{n}, s_{1}} = q_{s_{1}, s_{n}} \cdot q_{s_{n}, s_{n - 1}} \cdot \ldots \cdot q_{s_{2}, s_{1}}\) for all \(n \in \mathbb {N}_{\ge 2}\) and distinct \(s_{1}, \dots , s_{n} \in \mathcal {S}\) [13].
Time reversibility of CTMC-based compositional models of concurrent systems has been investigated in [8]. More precisely, conditions relying on the conservation of total exit rates of states and of rate products around cycles are examined, which support the hierarchical and compositional reversal of stochastic process algebra terms. These conditions also lead to the efficient calculation of steady-state probability distributions in a product form typical of queueing theory [15], thus avoiding the need of solving the global balance equation system. More recently, in [25] similar conditions have been employed to characterize the class of \(\rho \)-reversible stochastic automata. Under certain constraints, the joint steady-state probability distribution of the composition of two such automata is the product of the steady-state probability distributions of the two automata.
4 Integrating Causal and Time Reversibility
In this section, we integrate the two concepts of causal consistent reversibility and time reversibility recalled in the previous two sections. To do so, we start with a simple calculus called RMPC – Reversible Markovian Process Calculus, in which actions are paired with rates, whose syntax and semantics are inspired by the approach of [28]. Then, we show that the reversibility induced by RMPC is causal consistent by importing the notion of concurrent transitions from [5]. Finally, we exhibit the conditions under which time reversibility is achieved too and we compare our setting, in which time reversibility is ensured by construction, with those of [8, 25].
4.1 Syntax and Semantics for RMPC
The syntax of RMPC is shown in Table 1. A forward process P can be one of the following: the idle process \(\mathbf {0}\); the prefixed process \((a, \lambda ). P\), which is able to perform an action a at rate \(\lambda \) and then continues as process P; the nondeterministic choice \(P + Q\) between processes P and Q; or the cooperation \(P \parallel _{L} Q\), indicating that processes P and Q execute in parallel and must synchronise only on actions prescribed by the set L.
A reversible process R is built on top of forward processes. As in [28], the syntax of reversible processes differs from the one of forward processes by the fact that in the former each prefix \((a, \lambda )\) can be decorated with a communication key i thus becoming \((a, \lambda )[i]\). A process of the form \((a, \lambda )[i]. R\) expresses that in the past the process synchronised with the environment and this synchronisation was identified by key i. Keys are thus attached only to already executed actions.
Let \(\mathcal {A}\) be the set of actions such that \(a, b \in \mathcal {A}\), \(\mathcal {R}= \mathbb {R}_{> 0}\) be the set of rates such that \(\lambda , \mu \in \mathcal {R}\), and \(\mathcal {K}\) be the set of keys such that \(i, j \in \mathcal {K}\). Let \(\mathcal {L}= \mathcal {A}\times \mathcal {R}\times \mathcal {K}\) be the set of labels each formed by an action, a rate, and a communication key. We let \(\ell \) and its decorated versions range over \(\mathcal {L}\). Moreover, given a forward label \(\ell = (a, \lambda )[i]\), we denote by \(\overline{\ell } = (a, \overline{\lambda })[i]\) the corresponding backward label. Finally, \(\mathcal {P}\) is the set of processes generated by the production for R in Table 1.
Definition 1
(standard process). Process \(R \in \mathcal {P}\) is standard, written \(\mathtt {std}(R)\), iff it can be derived from the production for P in Table 1.
Definition 2
(process key). The set of keys of process \(R \in \mathcal {P}\), written \(\mathtt {key}(R)\), is inductively defined as follows:
The semantics for RMPC is defined as a labeled transition system  . Like in [28], the transition relation
. Like in [28], the transition relation  is given by
is given by  , where the forward transition relation \(\xrightarrow {\;\;}\) and the backward transition relation
, where the forward transition relation \(\xrightarrow {\;\;}\) and the backward transition relation  are the least relations respectively induced by the forward rules in the left part and the backward rules in the right part of Table 2.
are the least relations respectively induced by the forward rules in the left part and the backward rules in the right part of Table 2.
Rule Act1 deals with prefixed processes of the form \((a,\lambda ).P\), with P written as R subject to \(\mathtt {std}(R)\). In addition to transforming the action prefix into a transition label, it generates a fresh key i, which is bound to the action \((a,\lambda )\) thus yielding the label \((a,\lambda )[i]\). As we can note, the prefix is not discarded by the application of the rule, instead it becomes a key-storing decoration in the target process. Rule Act1\(^\bullet \) reverts the action \((a,\lambda )[i]\) of the process \((a,\lambda )[i].R\) provided that R is a standard process, which ensures that \((a,\lambda )[i]\) is the only past action that is left to undo. One of the main design choices of the entire framework is how the rate \(\overline{\lambda }\) of the backward action is calculated. For the time being, we leave it unspecified in Act1\(^\bullet \) as the value of this rate is not necessary to prove the causal consistency part of reversibility, but as we will see later on it is important in the proof of time reversibility.
The presence of rules Act2 and Act2\(^\bullet \) is motivated by the fact that rule Act1 does not discard the executed prefix from the process it generates. In particular, rule Act2 allows a prefixed process \((a,\lambda )[i].R\) to execute if R can itself execute, provided that the action performed by R picks a key j different from i. Rule Act2\(^\bullet \) simply propagates the execution of backward actions from inner subprocesses that are not standard as long as key uniqueness is preserved.
Unlike the classical rules of the choice operator [26], rule Cho does not discard the context, i.e., the part of the process that has not contributed to the action. More in detail, if the process \(R + S\) does an action, say \((a,\lambda )[i]\), and becomes \(R'\), then the entire process becomes \(R' + S\). In this way, the information about \(+ \, S\) is preserved. Furthermore, since S is a standard process because of the premise \(\mathtt {std}(S)\), it will never execute even if it is present in the process \(R' + S\). Hence, the \(+ \, S\) can be seen as a decoration, or a dead context, of process R. Note that, in order to apply rule Cho, at least one of the two processes has to be standard, meaning that it is impossible for two non-standard processes to execute if they are composed by a choice operator. Rule Cho\(^\bullet \) has precisely the same structure as rule Cho, but uses the backward transition relation. For both rules, we omit their symmetric variants in which it is S to move.
The semantics of cooperation is inspired by [11]. Rule Par allows process R within \(R \parallel _{L} S\) to individually perform an action \((a,\lambda )[i]\), provided that \(a \notin L\). Rule Coo allows R and S to cooperate through any action in the set L, provided that the communication key is the same on both sides. For the sake of simplicity, the rate of the cooperation action is assumed to be the product of the rates of the two involved actions [9]. Rules Par\(^\bullet \) and Coo\(^\bullet \) respectively have the same structure as Par and Coo; the symmetric variants of Par and Par\(^\bullet \) are omitted.
Not all the processes generated by the grammar in Table 1 are meaningful as, e.g., there might be several action prefixes sharing the same key in a sequential process, i.e., a process without occurrences of the cooperation operator. We only consider processes that are initial or reachable in the following sense:
Definition 3
(initial and reachable process). Process \(R \in \mathcal {P}\) is initial iff \(\mathtt {std}(R)\) holds. Process \(R \in \mathcal {P}\) is reachable iff it is initial or can be derived from an initial one via finitely many applications of the rules for \(\xrightarrow {\;\;}\) in Table 2.
4.2 Properties Preliminary to Reversibility
A basic property to satisfy in order for RMPC to be reversible is the so called loop lemma [5, 28], which will be exploited to establish both causal consistent reversibility and time reversibility. This property states that each transition of a reachable process can be undone. Formally:
Lemma 1
(loop lemma). Let \(R \in \mathcal {P}\) be a reachable process. Then \(R \xrightarrow {(a,\lambda )[i]} S\) iff  .
.
Proof
We proceed by induction on the depth of the derivation of \(R \xrightarrow {(a,\lambda )[i]} S\) (resp.,  ), by noticing that for each forward (resp., backward) rule there exists a corresponding backward (resp., forward) one.
), by noticing that for each forward (resp., backward) rule there exists a corresponding backward (resp., forward) one.

The lemma generalizes as follows. For any sequence \(\sigma \) of \(n \in \mathbb {N}_{> 0}\) labels \(\ell _1, \dots , \ell _n\), let \(R \xrightarrow {\sigma } S\) be the corresponding forward sequence of transitions \(R \xrightarrow {\ell _1} R_1 \xrightarrow {\ell _2} \cdots \xrightarrow {\ell _n} S\) and \(\overline{\sigma }\) be the corresponding backward sequence such that, for each \(\ell _i\) occurring in \(\sigma \), it holds that \(R_{i-1} \xrightarrow {\ell _i} R_i\) iff  . A direct consequence of the loop lemma is the following:
. A direct consequence of the loop lemma is the following:
Corollary 1
Let \(R \in \mathcal {P}\) be a reachable process. Then  iff
iff  .
.
4.3 Causal Consistent Reversibility for RMPC
In order to prove the causal consistent reversibility of RMPC, we borrow some machinery from [5] that needs to be adapted as the reversing method of [28] we are using is different from the one of [5]. In particular, we import the notion of concurrent transitions.
Given a transition  with \(R, S \in \mathcal {P}\) reachable processes, we call R the source of \(\theta \) and S its target. Two transitions are said to be coinitial if they have the same source, and cofinal if they have the same target. A sequence of pairwise composable transitions is called a computation, where composable means that the target of any transition in the sequence is the source of the next transition. We let \(\theta \) and its decorated variants range over transitions, while \(\omega \) and its decorated variants range over computations. If \(\theta \) is a forward transition, i.e., \(\theta : R \xrightarrow {\ell } S\), we denote its backward version
with \(R, S \in \mathcal {P}\) reachable processes, we call R the source of \(\theta \) and S its target. Two transitions are said to be coinitial if they have the same source, and cofinal if they have the same target. A sequence of pairwise composable transitions is called a computation, where composable means that the target of any transition in the sequence is the source of the next transition. We let \(\theta \) and its decorated variants range over transitions, while \(\omega \) and its decorated variants range over computations. If \(\theta \) is a forward transition, i.e., \(\theta : R \xrightarrow {\ell } S\), we denote its backward version  as \(\overline{\theta }\). The notions of source, target, and composability extend naturally to computations. We indicate with \(\epsilon _{R}\) the empty computation whose source is R and with \(\omega _1;\omega _2\) the composition of two composable computations \(\omega _1\) and \(\omega _2\).
as \(\overline{\theta }\). The notions of source, target, and composability extend naturally to computations. We indicate with \(\epsilon _{R}\) the empty computation whose source is R and with \(\omega _1;\omega _2\) the composition of two composable computations \(\omega _1\) and \(\omega _2\).
Before specifying when two transitions are concurrent, we need to define the set of causes – identified by keys – of a given communication key.
Definition 4
(causal set). Let \(R \in \mathcal {P}\) be a reachable process and \(i \in \mathtt {key}(R)\). The causal set \(\mathtt {cau}(R,i)\) is inductively defined as follows for \(j \ne i\):
where \(\mathtt {cau}'(R,i) = \mathtt {cau}(R,i)\) if \(i \in \mathtt {key}(R)\) and \(\mathtt {cau}'(R,i) = \emptyset \) otherwise.
If \(i \in \mathtt {key}(R)\), then \(\mathtt {cau}(R, i)\) represents the set of keys in R that caused i, with \(\mathtt {cau}(R, i) \subset \mathtt {key}(R)\) since \(i \notin \mathtt {cau}(R, i)\) and keys not causally related to i are not considered. A key j causes i if it appears syntactically before i in R or, said otherwise, i is inside the scope of j. We are now in place to define what we mean by concurrent transitions:
Definition 5
(concurrent transitions). Two coinitial transitions \(\theta _1\) and \(\theta _2\) from a reachable process \(R \in \mathcal {P}\) are in conflict iff one of the following holds:
-
1.
\(\theta _1 : R \xrightarrow {(a,\lambda )[j]} S_1\) and
 with \(i \in \mathtt {cau}(S_1,j)\).
with \(i \in \mathtt {cau}(S_1,j)\). -
2.
\(R = R_1 + R_2\) with \(\theta _k\) deriving from \(R_k \xrightarrow {(a_k,\lambda _k)[i_k]} S_k\) for \(k = 1, 2\).
Two coinitial transitions are concurrent when they are not in conflict.
The first condition above just tells that a forward transition is in conflict with a backward one whenever the latter tries to undo a cause of the key of the former. The second condition deems as conflictual two transitions respectively generated by the two subprocesses of a choice operator. Figure 1 shows two related examples. In the first case, the process \((a,\lambda )[i].(b,\mu ).P\) can perform two transitions: a backward one and a forward one. They meet the first condition of Definition 5 as the backward transition removes the key i that is in the causal set of j. In the second case, we have that process \((a,\lambda ).P+(a,\lambda ).P\) is able to trigger two forward transitions. Since they arise from the same choice operator, they are in conflict according to the second condition of Definition 5.
Remark 1
It is worth noting that in a stochastic process calculus like RMPC the semantic treatment of the choice operator is problematic [10] because a process of the form \((a,\lambda ).P + (a,\lambda ).P\) should produce either a single a-transition whose rate is \(\lambda + \lambda \), or two a-transitions each having rate \(\lambda \) that do not collapse into a single one. In our reversible framework, two distinct transitions are generated thanks to the fact that the key associated with the executed action is stored into the derivative process too, as shown in the bottom part of Fig. 1.
Concurrent transitions can commute, while conflicting ones cannot. Formally:
Lemma 2
(diamond lemma). Let  and
and  be two coinitial transitions from a reachable process \(R \in \mathcal {P}\). If \(\theta _1\) and \(\theta _2\) are concurrent, then there exist two cofinal transitions
be two coinitial transitions from a reachable process \(R \in \mathcal {P}\). If \(\theta _1\) and \(\theta _2\) are concurrent, then there exist two cofinal transitions  and
and  .
.
Proof
By case analysis on the form of \(\theta _1\) and \(\theta _2\).

We are now in a position to show that reversibility in our framework is causally consistent. Following [23], we first define a notion of causal equivalence between computations that abstracts from the order of concurrent transitions. We formalize \(\asymp \) as the least equivalence relation over computations that is closed under composition and obeys the following rules:
Equivalence \(\asymp \) states that if we have two concurrent transitions, then the two computations obtained by swapping the order of their execution are the same, and that any computation composed by a transition followed by its inverse is equivalent to the empty computation. The proof of causal consistency relying on \(\asymp \) follows that of [5], although the arguments are different due to the fact that the notion of concurrent transitions is formalized differently.
The following lemma says that, up to causal equivalence, one can always reach for the maximum freedom of choice among transitions, meaning that it is possible to undo all the executed actions and then restart.
Lemma 3
(rearranging lemma). For any computation \(\omega \) there exist two forward computations \(\omega _1\) and \(\omega _2\) such that \(\omega \asymp \overline{\omega _1};\omega _2\).
Proof
By induction on the length of \(\omega \) and on the distance (intended as number of transitions) between the beginning of \(\omega \) and the earliest pair of consecutive transitions in \(\omega \) such that the former is forward while the latter is backward. The analysis uses both the loop lemma (Lemma 1) and the diamond lemma (Lemma 2).

The following lemma says that if two computations \(\omega _1\) and \(\omega _2\) are coinitial and cofinal and \(\omega _2\) is made of forward transitions only, then in \(\omega _1\) there are some transitions that are later undone. This computation is thus causally equivalent to a forward one in which the undone transitions do not take place at all.
Lemma 4
(shortening lemma). Let \(\omega _1\) and \(\omega _2\) be coinitial and cofinal computations, with \(\omega _2\) forward. Then there exists a forward computation \(\omega '_1\) of length at most that of \(\omega _1\) such that \(\omega '_1 \asymp \omega _1\).
Proof
The proof is by induction on the length of \(\omega _1\), using the diamond lemma (Lemma 2) and the rearranging lemma (Lemma 3). In the proof, the forward computation \(\omega _2\) is the main guideline for shortening \(\omega _1\) into a forward computation. Indeed, the proof relies crucially on the fact that \(\omega _1\) and \(\omega _2\) share the same source and the same target and that \(\omega _2\) is a forward computation.

Theorem 1
(causal consistency). Let \(\omega _1\) and \(\omega _2\) be coinitial computations. Then \(\omega _1 \asymp \omega _2\) iff \(\omega _1\) and \(\omega _2\) are cofinal too.
Proof
The ‘if’ direction follows by definition of causal equivalence and computation composition. The ‘only if’ direction exploits the diamond lemma (Lemma 2), the rearranging lemma (Lemma 3), and the shortening lemma (Lemma 4).

With Theorem 1 we have proved that the notion of causal equivalence characterises a space for admissible rollbacks that are (i) consistent in the sense that they do not lead to previously unreachable states and (ii) flexible enough to allow undo operations to be rearranged. This implies that the states reached by a backward computation could be reached by performing forward computations only. We can therefore conclude that RMPC is causal consistent reversible.
4.4 Time Reversibility for RMPC
The rules in Table 2 associate with any initial process \(R \in \mathcal {P}\) a labeled transition system  . To investigate time reversibility, we have to derive from \([\![R ]\!]\) the CTMC \(\mathcal {M}[\![R ]\!]\) underlying R and we have to specify how each backward rate \(\overline{\lambda }\) is obtained from the corresponding forward rate \(\lambda \).
. To investigate time reversibility, we have to derive from \([\![R ]\!]\) the CTMC \(\mathcal {M}[\![R ]\!]\) underlying R and we have to specify how each backward rate \(\overline{\lambda }\) is obtained from the corresponding forward rate \(\lambda \).
First of all, we observe that every non-terminal state of \([\![R ]\!]\) has infinitely many outgoing transitions. The reason is that rules Act1 and Act2 generate a transition for each possible admissible key, with the key being part of both the label and the derivative process term. On the one hand, this is useful for avoiding the generation of a single \((a, \lambda )\)-transition in the case of a process like \((a, \lambda ) . P + (a, \lambda ) . P\) whose overall exit rate is \(\lambda + \lambda \); even if the key is the same, two different states \((a, \lambda )[i] . P + (a, \lambda ) . P\) and \((a, \lambda ) . P + (a, \lambda )[i] . P\) are reached. On the other hand, it requires considering transition bundles to build \(\mathcal {M}[\![R ]\!]\).
We call transition bundle a set of transitions departing from the same state and labeled with the same action/rate but different keys, whose target states are syntactically identical up to keys. Formally, we denote by \(\equiv _{\mathcal {K}}\) the least equivalence relation over \(\mathcal {P}\) induced by \((a, \lambda )[i] . S \equiv _{\mathcal {K}} (a, \lambda )[j] . S\). We then define the CTMC underlying an initial process \(R \in \mathcal {P}\) as the labeled transition system  where:
where:
-
\(\mathcal {P}/ \! \equiv _{\mathcal {K}}\) is the quotient set of \(\equiv _{\mathcal {K}}\) over \(\mathcal {P}\), i.e., the set of classes of processes that are equivalent to each other according to \(\equiv _{\mathcal {K}}\).
-
\([R]_{\equiv _{\mathcal {K}}}\) is the equivalence class of R with respect to \(\equiv _{\mathcal {K}}\), which simply is the singleton set \(\{ R \}\) as R is initial and hence contains no keys.
-
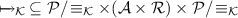 is the transition relation given by
is the transition relation given by  such that \([R]_{\equiv _{\mathcal {K}}} \xrightarrow {(a, \lambda )}_{\mathcal {K}} [R']_{\equiv _{\mathcal {K}}}\) whenever \(R \xrightarrow {(a, \lambda )[i]} R'\) for some \(i \in \mathcal {K}\) and
such that \([R]_{\equiv _{\mathcal {K}}} \xrightarrow {(a, \lambda )}_{\mathcal {K}} [R']_{\equiv _{\mathcal {K}}}\) whenever \(R \xrightarrow {(a, \lambda )[i]} R'\) for some \(i \in \mathcal {K}\) and  whenever
whenever  for some \(i \in \mathcal {K}\).
for some \(i \in \mathcal {K}\).
When moving from \([\![R ]\!]\) to \(\mathcal {M}[\![R ]\!]\), individual states are replaced by classes of states that are syntactically identical up to keys in the same positions, moreover keys are removed from transition labels. As a consequence, every state of \(\mathcal {M}[\![R ]\!]\) turns out to have finitely many outgoing transitions. We also note that \(\mathcal {M}[\![R ]\!]\) is an action-labeled CTMC, as each of its transitions is labeled with both a rate and an action.
As a preliminary step towards time reversibility, we have to show that \(\mathcal {M}[\![R ]\!]\) is stationary. It holds that \(\mathcal {M}[\![R ]\!]\) is even ergodic thanks to the loop lemma.
Lemma 5
Let \(R \in \mathcal {P}\) be an initial process. Then \(\mathcal {M}[\![R ]\!]\) is time homogeneous and ergodic.
Proof
The time homogeneity of \(\mathcal {M}[\![R ]\!]\) is a straightforward consequence of the fact that its rates simply are positive real numbers, not time-dependent functions. The ergodicity of \(\mathcal {M}[\![R ]\!]\) stems from the fact that the graph representation of the considered CTMC is a finite, strongly connected component due to Corollary 1.

We exploit once more the loop lemma to derive that, in the case that \(\overline{\lambda } = \lambda \), the steady-state probability distribution of \(\mathcal {M}[\![R ]\!]\) is the uniform distribution, from which time reversibility will immediately follow.
Lemma 6
Let \(R \in \mathcal {P}\) be an initial process, \(\mathcal {S}\) be the set of states of \(\mathcal {M}[\![R ]\!]\), and \(n = |\mathcal {S}|\). If every backward rate is equal to the corresponding forward rate, then the steady-state probability distribution \(\varvec{\pi }\) of \(\mathcal {M}[\![R ]\!]\) satisfies \(\pi (s) = 1 / n\) for all \(s \in \mathcal {S}\).
Proof
If \(n = 1\), i.e., R is equal to \(\mathbf {0}\) or to the cooperation of several processes whose initial actions have to synchronize but are different from each other, then trivially \(\pi (s) = 1 / n = 1\) for the only state \(s \in \mathcal {S}\).
Suppose now that \(n \ge 2\). From Lemma 5, it follows that \(\mathcal {M}[\![R ]\!]\) has a unique steady-state probability distribution \(\varvec{\pi }\). Due to Lemma 1, the global balance equation for an arbitrary \(s \in \mathcal {S}\) is as follows:

Since every backward rate is equal to the corresponding forward rate, the global balance equation for s boils down to:

Since the two summations have the same number of summands, the equation above is satified when \(\pi (s) = \pi (s')\) for all \(s' \in \mathcal {S}\) reached by a transition from s. All global balance equations are thus satisfied when \(\pi (s) = 1 / n\) for all \(s \in \mathcal {S}\).

Theorem 2
(time reversibility). Let \(R \in \mathcal {P}\) be an initial process. If every backward rate is equal to the corresponding forward rate, then \(\mathcal {M}[\![R ]\!]\) is time reversible.
Proof
Let \(\mathcal {S}\) be the set of states of \(\mathcal {M}[\![R ]\!]\) and \(n = |\mathcal {S}|\). From Lemma 5, it follows that \(\mathcal {M}[\![R ]\!]\) has a unique steady-state probability distribution \(\varvec{\pi }\). To avoid trivial cases, suppose \(n \ge 2\) and consider \(s, s' \in \mathcal {S}\) with \(s \ne s'\) connected by a transition. Due to Lemma 1, the partial balance equation for s and \(s'\) is as follows:

Since every backward rate is equal to the corresponding forward rate, the partial balance equation for s and \(s'\) boils down to:

Since the two summations have the same number of summands and \(\pi (s) = \pi (s') = 1 / n\) due to Lemma 6, the equation above is satified. The result then follows from the fact that s and \(s'\) are two arbitrary distinct states connected by a transition.

The main difference between our approach to time reversibility and the ones of [8, 25] is twofold. Firstly, our approach is part of a more general framework in which also causal consistent reversibility is addressed. Secondly, our approach is inspired by the idea of [28] of developing a formalism in which it is possible to express models whose reversibility is guaranteed by construction, instead of building a posteriori the time-reversed version of a certain model like in [8] or verifying a posteriori whether a given model is time reversible or not like in [25].
It is worth noting that these methodological differences do not prevent us from adapting to our setting some results from [8, 25], although a few preliminary observations about notational differences are necessary.
Both [8] and [25] make a distinction between active actions, each of which is given a rate, and passive actions, each of which is given a weight, with the constraint that, in case of synchronization, the rate of the active action is multiplied by the weight of the corresponding passive action. In RMPC there is no such distinction, however the same operation, i.e., multiplication, is applied to the rates of two synchronizing actions. A passive action can thus be rendered as an action with rate 1, while a set of alternative passive actions can be rendered as a set of actions whose rates sum up to 1. Moreover, in [25] synchronization is enforced between any active-passive pair of identical actions, whereas in RMPC the cooperation operator is enriched with an explicit synchronization set L, which yields as a special case the aforementioned synchronization discipline when L is equal to the set \(\mathcal {A}\) of all the actions. We can therefore conclude that our cooperation operator is a generalization of those used in [8, 25], hence the recalled notational differences do not hamper result transferral.
In [8] the compositionality of a CTMC-based stochastic process calculus is exploited to prove the reversed compound agent theorem (RCAT), which establishes the conditions under which the time-reversed version of the cooperation of two processes is equal to the cooperation of the time-reversed versions of those two processes. The application of RCAT leads to product-form solution results from stochastic process algebraic models, including a new different proof of Jackson theorem for product-form queueing networks [12].
In [25] the notion of \(\rho \)-reversibility is introduced for stochastic automata, which are essentially action-labeled CTMCs. Function \(\rho \) is a state permutation that ensures (i) for each action the equality of the total exit rate of any state s and \(\rho (s)\) and (ii) the conservation of action-related rate products across cycles when considering states in the forward direction and their \(\rho \)-counterparts in the backward direction. For any ergodic \(\rho \)-reversible automaton, it turns out that \(\pi (s) = \pi (\rho (s))\) for every state s. Moreover, the synchronization inspired by [31] of two \(\rho \)-reversible stochastic automata is still \(\rho \)-reversible and, in case of ergodicity, under certain conditions the steady-state probability of any compound state is the product of the steady-state probabilities of the two constituent states.
Our time reversibility result for RMPC can be rephrased in the setting of [25] in terms of \(\rho \)-reversibility with \(\rho \) being the identity function over states. As a consequence, the following two results stem from Theorem 2 of the present paper and, respectively, Theorems 2 and 3 of [25]:
Corollary 2
(time reversibility closure). Let \(R, S \in \mathcal {P}\) be initial processes and \(L \subseteq \mathcal {A}\). If every backward rate is equal to the corresponding forward rate, then \(\mathcal {M}[\![R \parallel _{L} S ]\!]\) is time reversible too.
Corollary 3
(product form). Let \(R, S \in \mathcal {P}\) be initial processes and \(L \subseteq \mathcal {A}\). If every backward rate is equal to the corresponding forward rate and the set of states \(\mathcal {S}\) of \(\mathcal {M}[\![R \parallel _{L} S ]\!]\) is equal to \(\mathcal {S}_{R} \times \mathcal {S}_{S}\) where \(\mathcal {S}_{R}\) is the set of states of \(\mathcal {M}[\![R ]\!]\) and \(\mathcal {S}_{S}\) is the set of states of \(\mathcal {M}[\![S ]\!]\), then \(\pi (r, s) = \pi _{R}(r) \cdot \pi _{S}(s)\) for all \((r, s) \in \mathcal {S}_{R} \times \mathcal {S}_{S}\).
The product form result above avoids the calculation of the global balance equations over \(\mathcal {M}[\![R \parallel _{L} S ]\!]\), as \(\pi (r, s)\) can simply be obtained by multiplying \(\pi _{R}(r)\) with \(\pi _{S}(s)\). However, the condition \(\mathcal {S}= \mathcal {S}_{R} \times \mathcal {S}_{S}\) requires to check that every state in the full Cartesian product is reachable from \(R \parallel _{L} S\). This means that no compound state is such that its constituent states enable some action, but none of the enabled actions can be executed due to the constraints imposed by the synchronization set L. The condition \(\mathcal {S}= \mathcal {S}_{R} \times \mathcal {S}_{S}\) implies that \(\mathcal {M}[\![R \parallel _{L} S ]\!]\) is ergodic over the full Cartesian product of the two original state spaces, which is the condition used in [25]. Although implicit in the statement of the corollary, the time reversibility of \(\mathcal {M}[\![R \parallel _{L} S ]\!]\) is essential for the product form result.
5 Conclusions
Different interpretations of reversibility are present in the literature. In this paper, we have started our research quest towards bridging causal consistent reversibility [5] – developed in concurrency theory – and time reversibility [13] – originated in the field of stochastic processes. We have accomplished this by introducing the stochastic process calculus RMPC, whose syntax and semantics follow the approach of [28], thus paving the way to concurrent system models that are both causal consistent reversible and time reversible by construction. Based on time reversibility, we have also adapted from [25] a product form result that enables the efficient calculation of performance measures.
There are several lines of research that we plan to undergo, ranging from the application of our results to examples and case studies modeled with RMPC to the development of further theoretical results. For instance, we would like to investigate other conditions under which time reversibility is achieved, in addition to the one relying on the equality of forward and backward rates.
Moreover, we observe that the syntax of RMPC does not include recursion. From the point of view of the ergodicity of the underlying CTMC, this is not a problem because every forward transition has the corresponding backward transition by construction. However, there might be situations in which recursion is necessary to appropriately describe the behavior of a system. Because of the use of communication keys, a simple process of the form \(P \triangleq (a,\lambda ).P\), whose standard labeled transition system features a single state with a self-looping transition, produces a sequence of infinitely many distinct states even if we resort to transition bundles. Our claim is that the specific cooperation operator that we have considered may require a mechanism lighter than communications keys to keep track of past actions, which may avoid the generation of an infinite state space in the presence of recursion.
References
Baeten, J.C.M., Verhoef, C.: A congruence theorem for structured operational semantics with predicates. In: Best, E. (ed.) CONCUR 1993. LNCS, vol. 715, pp. 477–492. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-57208-2_33
Barylska, K., Koutny, M., Mikulski, L., Piatkowski, M.: Reversible computation vs. reversibility in Petri nets. Sci. Comput. Program. 151, 48–60 (2018)
Bennett, C.H.: Logical reversibility of computations. IBM J. Res. Dev. 17, 525–532 (1973)
Cristescu, I., Krivine, J., Varacca, D.: A compositional semantics for the reversible \(\pi \)-calculus. In: Proceedings of LICS 2013, pp. 388–397. IEEE-CS Press (2013)
Danos, V., Krivine, J.: Reversible communicating systems. In: Gardner, P., Yoshida, N. (eds.) CONCUR 2004. LNCS, vol. 3170, pp. 292–307. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28644-8_19
Danos, V., Krivine, J.: Transactions in RCCS. In: Abadi, M., de Alfaro, L. (eds.) CONCUR 2005. LNCS, vol. 3653, pp. 398–412. Springer, Heidelberg (2005). https://doi.org/10.1007/11539452_31
Giachino, E., Lanese, I., Mezzina, C.A.: Causal-consistent reversible debugging. In: Gnesi, S., Rensink, A. (eds.) FASE 2014. LNCS, vol. 8411, pp. 370–384. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54804-8_26
Harrison, P.G.: Turning back time in Markovian process algebra. Theoret. Comput. Sci. 290(3), 1947–1986 (2003)
Hillston, J.: The nature of synchronisation. In: Proceedings of PAPM 1994, pp. 51–70. University of Erlangen, Technical Report 27–4 (1994)
Hillston, J.: A Compositional Approach to Performance Modelling. Cambridge University Press, Cambridge (1996)
Hoare, C.A.R.: Communicating Sequential Processes. Prentice Hall, Upper Saddle River (1985)
Jackson, J.R.: Jobshop-like queueing systems. Manage. Sci. 10(1), 131–142 (1963)
Kelly, F.P.: Reversibility and Stochastic Networks. Wiley, Chichester (1979)
Kemeny, J.G., Snell, J.L.: Finite Markov Chains. Van Nostrand, New York (1960)
Kleinrock, L.: Queueing Systems. Wiley, New York (1975)
Landauer, R.: Irreversibility and heat generated in the computing process. IBM J. Res. Dev. 5, 183–191 (1961)
Lanese, I., Lienhardt, M., Mezzina, C.A., Schmitt, A., Stefani, J.-B.: Concurrent flexible reversibility. In: Felleisen, M., Gardner, P. (eds.) ESOP 2013. LNCS, vol. 7792, pp. 370–390. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37036-6_21
Lanese, I., Medić, D., Mezzina, C.A.: Static versus dynamic reversibility in CCS. Acta Informatica (2019)
Lanese, I., Mezzina, C.A., Stefani, J.-B.: Reversing higher-order \(\pi \). In: Gastin, P., Laroussinie, F. (eds.) CONCUR 2010. LNCS, vol. 6269, pp. 478–493. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15375-4_33
Lanese, I., Nishida, N., Palacios, A., Vidal, G.: CauDEr: a causal-consistent reversible debugger for erlang. In: Gallagher, J.P., Sulzmann, M. (eds.) FLOPS 2018. LNCS, vol. 10818, pp. 247–263. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-90686-7_16
Lanese, I., Nishida, N., Palacios, A., Vidal, G.: A theory of reversibility for Erlang. J. Log. Algeb. Meth. Program. 100, 71–97 (2018)
Laursen, J.S., Ellekilde, L.P., Schultz, U.P.: Modelling reversible execution of robotic assembly. Robotica 36(5), 625–654 (2018)
Lévy, J.J.: An algebraic interpretation of the \(\lambda \beta \)K-calculus; and an application of a labelled \(\lambda \)-calculus. Theoret. Comput. Sci. 2(1), 97–114 (1976)
Lienhardt, M., Lanese, I., Mezzina, C.A., Stefani, J.-B.: A reversible abstract machine and its space overhead. In: Giese, H., Rosu, G. (eds.) FMOODS/FORTE -2012. LNCS, vol. 7273, pp. 1–17. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-30793-5_1
Marin, A., Rossi, S.: Quantitative analysis of concurrent reversible computations. In: Sankaranarayanan, S., Vicario, E. (eds.) FORMATS 2015. LNCS, vol. 9268, pp. 206–221. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-22975-1_14
Milner, R.: Communication and Concurrency. Prentice Hall, Upper Saddle River (1989)
Perumalla, K.S., Park, A.J.: Reverse computation for rollback-based fault tolerance in large parallel systems - evaluating the potential gains and systems effects. Cluster Comput. 17(2), 303–313 (2014)
Phillips, I.C.C., Ulidowski, I.: Reversing algebraic process calculi. J. Logic Algeb. Program. 73(1–2), 70–96 (2007)
Phillips, I., Ulidowski, I., Yuen, S.: A reversible process calculus and the modelling of the ERK signalling pathway. In: Glück, R., Yokoyama, T. (eds.) RC 2012. LNCS, vol. 7581, pp. 218–232. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36315-3_18
Michele Pinna, G.: Reversing steps in membrane systems computations. In: Gheorghe, M., Rozenberg, G., Salomaa, A., Zandron, C. (eds.) CMC 2017. LNCS, vol. 10725, pp. 245–261. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-73359-3_16
Plateau, B.: On the stochastic structure of parallelism and synchronization models for distributed algorithms. In: Proceedings of SIGMETRICS 1985, pp. 147–154. ACM Press (1985)
Schordan, M., Oppelstrup, T., Jefferson, D.R., Barnes Jr., P.D.: Generation of reversible C++ code for optimistic parallel discrete event simulation. New Gener. Comput. 36(3), 257–280 (2018)
Siljak, H., Psara, K., Philippou, A.: Distributed antenna selection for massive MIMO using reversing Petri nets. IEEE Wirel. Commun. Lett. 8(5), 1427–1430 (2019)
Stewart, W.J.: Introduction to the Numerical Solution of Markov Chains. Princeton University Press, Princeton (1994)
Vassor, M., Stefani, J.-B.: Checkpoint/rollback vs causally-consistent reversibility. In: Kari, J., Ulidowski, I. (eds.) RC 2018. LNCS, vol. 11106, pp. 286–303. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-99498-7_20
de Vries, E., Koutavas, V., Hennessy, M.: Communicating transactions. In: Gastin, P., Laroussinie, F. (eds.) CONCUR 2010. LNCS, vol. 6269, pp. 569–583. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15375-4_39
Acknowledgement
We would like to thank Andrea Marin for the valuable discussions on time reversibility. The second author has been partially supported by the French ANR project DCore ANR-18-CE25-0007 and by the Italian INdAM – GNCS project 2020 Reversible Concurrent Systems: From Models to Languages.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 IFIP International Federation for Information Processing
About this paper
Cite this paper
Bernardo, M., Mezzina, C.A. (2020). Towards Bridging Time and Causal Reversibility. In: Gotsman, A., Sokolova, A. (eds) Formal Techniques for Distributed Objects, Components, and Systems. FORTE 2020. Lecture Notes in Computer Science(), vol 12136. Springer, Cham. https://doi.org/10.1007/978-3-030-50086-3_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-50086-3_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-50085-6
Online ISBN: 978-3-030-50086-3
eBook Packages: Computer ScienceComputer Science (R0)






 with
with 
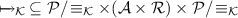 is the transition relation given by
is the transition relation given by  such that
such that  whenever
whenever  for some
for some 