Abstract
We introduce a novel comprehensive framework for epistemic reasoning in multi-agent systems where agents may behave asynchronously and may be byzantine faulty. Extending Fagin et al.’s classic runs-and-systems framework to agents who may arbitrarily deviate from their protocols, it combines epistemic and temporal logic and incorporates fine-grained mechanisms for specifying distributed protocols and their behaviors. Besides our framework’s ability to express any type of faulty behavior, from fully byzantine to fully benign, it allows to specify arbitrary timing and synchronization properties. As a consequence, it can be adapted to any message-passing distributed computing model we are aware of, including synchronous processes and communication, (un-)reliable uni-/multi-/broadcast communication, and even coordinated action. The utility of our framework is demonstrated by formalizing the brain-in-a-vat scenario, which exposes the substantial limitations of what can be known by asynchronous agents in fault-tolerant distributed systems. Given the knowledge of preconditions principle, this restricts preconditions that error-prone agents can use in their protocols. In particular, it is usually necessary to relativize preconditions with respect to the correctness of the acting agent.
...By our remembrances of days foregone
Such were our faults, or then we thought them none.
W. Shakespeare,
All’s Well That Ends Well
R. Kuznets—Supported by the Austrian Science Fund (FWF) project RiSE/SHiNE (S11405) and ADynNet (P28182).
K. Fruzsa—PhD student in the FWF doctoral program LogiCS (W1255).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
The term “byzantine” originated from [18]. Leslie Lamport chose a defunct country to avoid offending anyone living and also as a pun [26, p. 39] because generals from Byzantium could, in fact, be expected to behave in a byzantine (i.e., devious or treacherous) fashion. Unfortunately, this pun might be responsible for the ensuing unnecessary ([27]) capitalization of the word even for faults unrelated to Byzantium proper.
- 2.
Cf. “And whatsoever else shall hap to-night, Give it an understanding but no tongue.” W. Shakespeare, Hamlet, Act I, Scene 2.
- 3.
‘\({}:{}\)’ stands for concatenation.
- 4.
Prohibition (b) does not extend to actions, which need not be correctly recorded.
- 5.
In
 for byzantine sends or in
for byzantine sends or in 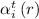 for correct ones that will be actually performed (see filtering stage 2).
for correct ones that will be actually performed (see filtering stage 2). - 6.
Arguments for are redundant here but will be used in future extensions.
- 7.
Full definitions of
 and
and  are presented in Appendix in Definition 16.
are presented in Appendix in Definition 16. - 8.
For connections to the semantic externalism and a survey of philosophical literature on the subject, see [25].
References
Ben-Zvi, I., Moses, Y.: Agent-time epistemics and coordination. In: Lodaya, K. (ed.) ICLA 2013. LNCS, vol. 7750, pp. 97–108. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36039-8_9
Ben-Zvi, I., Moses, Y.: Beyond Lamport’s happened-before: On time bounds and the ordering of events in distributed systems. J. ACM 61(2), 13 (2014). https://doi.org/10.1145/2542181
Castañeda, A., Gonczarowski, Y.A., Moses, Y.: Unbeatable consensus. In: Kuhn, F. (ed.) DISC 2014. LNCS, vol. 8784, pp. 91–106. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45174-8_7
Dwork, C., Moses, Y.: Knowledge and common knowledge in a Byzantine environment: Crash failures. Inf. Comput. 88(2), 156–186 (1990). https://doi.org/10.1016/0890-5401(90)90014-9
Ezekiel, J., Lomuscio, A.: Combining fault injection and model checking to verify fault tolerance, recoverability, and diagnosability in multi-agent systems. Inf. Comput. 254(2), 167–194 (2017). https://doi.org/10.1016/j.ic.2016.10.007
Fagin, R., Halpern, J.Y., Moses, Y., Vardi, M.Y.: Reasoning About Knowledge. MIT Press, Cambridge (1995)
Fagin, R., Halpern, J.Y., Moses, Y., Vardi, M.Y.: Common knowledge revisited. Ann. Pure Appl. Logic 96, 89–105 (1999). https://doi.org/10.1016/S0168-0072(98)00033-5
Fedoruk, A., Deters, R.: Improving fault-tolerance by replicating agents. In: AAMAS 2002, pp. 737–744. ACM (2002). https://doi.org/10.1145/544862.544917
Fruzsa, K.: Hope for epistemic reasoning with faulty agents! In: Proceedings of ESSLLI 2019 Student Session (2019, to appear)
Gonczarowski, Y.A., Moses, Y.: Timely common knowledge: Characterising asymmetric distributed coordination via vectorial fixed points. In: Schipper, B.C. (ed.) TARK XIV, pp. 79–93 (2013). https://arxiv.org/pdf/1310.6414.pdf
Goren, G., Moses, Y.: Silence. In: PODC 2018, pp. 285–294. ACM (2018). https://doi.org/10.1145/3212734.3212768
Halpern, J.Y., Moses, Y.: Knowledge and common knowledge in a distributed environment. J. ACM 37(3), 549–587 (1990). https://doi.org/10.1145/79147.79161
Halpern, J.Y., Moses, Y., Waarts, O.: A characterization of eventual Byzantine agreement. SIAM J. Comput. 31(3), 838–865 (2001). https://doi.org/10.1137/S0097539798340217
Hintikka, J.: Knowledge and Belief: An Introduction to the Logic of the Two Notions. Cornell University Press, Ithaca (1962)
Kalech, M., Kaminka, G.A.: On the design of coordination diagnosis algorithms for teams of situated agents. Artif. Intell. 171(8–9), 491–513 (2007). https://doi.org/10.1016/j.artint.2007.03.005
Kraus, S., Lehmann, D.: Knowledge, belief and time. Theor. Comput. Sci. 58, 155–174 (1988). https://doi.org/10.1016/0304-3975(88)90024-2
Kuznets, R., Prosperi, L., Schmid, U., Fruzsa, K., Gréaux, L.: Knowledge in Byzantine message-passing systems I: Framework and the causal cone. Technical report TUW-260549, TU Wien (2019). https://publik.tuwien.ac.at/files/publik_260549.pdf
Lamport, L., Shostak, R., Pease, M.: The Byzantine Generals Problem. ACM Trans. Program. Lang. Syst. 4(3), 382–401 (1982). https://doi.org/10.1145/357172.357176
Lomuscio, A., Qu, H., Raimondi, F.: MCMAS: A model checker for the verification of multi-agent systems. In: Bouajjani, A., Maler, O. (eds.) CAV 2009. LNCS, vol. 5643, pp. 682–688. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02658-4_55
McKinsey, M.: Skepticism and content externalism. In: Stanford Encyclopedia of Philosophy (2018). https://plato.stanford.edu/entries/skepticism-content-externalism/
Michel, R.: A categorical approach to distributed systems, expressibility and knowledge. In: Rudnicki, P. (ed.) PODS 1989, pp. 129–143. ACM (1989). https://doi.org/10.1145/72981.72990
Moses, Y.: Relating knowledge and coordinated action: The knowledge of preconditions principle. In: Ramanujam, R. (ed.) TARK 2015, pp. 231–245 (2015). https://doi.org/10.4204/EPTCS.215.17
Moses, Y., Shoham, Y.: Belief as defeasible knowledge. Artif. Intell. 64(2), 299–321 (1993). https://doi.org/10.1016/0004-3702(93)90107-M
Moses, Y., Tuttle, M.R.: Programming simultaneous actions using common knowledge. Algorithmica 3, 121–169 (1988). https://doi.org/10.1007/BF01762112
Pessin, A., Goldberg, S. (eds.): The Twin Earth Chronicles: Twenty Years of Reflection on Hilary Putnam’s the “Meaning of Meaning". M. E. Sharpe (1996)
Taubenfeld, G.: Distributed Computing Pearls. Morgan & Claypool Publishers (2018). https://doi.org/10.2200/S00845ED1V01Y201804DCT014
Trask, R.L.: Mind the Gaffe: The Penguin Guide to Common Errors in English. Penguin Books (2001)
van Ditmarsch, H.: Dynamics of lying. Synthese 191(5), 745–777 (2014). https://doi.org/10.1007/s11229-013-0275-3
Acknowledgments
We are grateful to Hans van Ditmarsch and Yoram Moses for extensive helpful comments on earlier versions of this paper. We also thank the anonymous reviewers for their comments and suggestions on related research.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Appendix
A Appendix
This section is dedicated to proving the Brain-in-a-Vat Lemma. Before engaging with the proof, we flesh out necessary details of how our framework operates.
For a function \(f :\varSigma \rightarrow \varTheta \) and a set \(X \subseteq \varSigma \) we use the following notation:  . For functions with multiple arguments, we allow ourselves to mix and match elements with sets of elements, e.g.,
. For functions with multiple arguments, we allow ourselves to mix and match elements with sets of elements, e.g.,  . As stated in Sect. 2, the function
. As stated in Sect. 2, the function  must be total and satisfy the following properties: for arbitrary \(i,j\in \mathcal {A}\), and
must be total and satisfy the following properties: for arbitrary \(i,j\in \mathcal {A}\), and  , and \(a \in Actions _{i}\), and \(b \in Actions _{j}\),
, and \(a \in Actions _{i}\), and \(b \in Actions _{j}\),
-
1.
 ;
; -
2.
 .
.
Thus, it is possible to define an inverse function on  :
:
Definition 14
We use a function \( local :\overline{{ GHaps }_{}}\longrightarrow Haps _{}\) converting correct haps from the global format into the local ones for the respective agents in such a way that, for any \(i \in \mathcal {A}\),  , and \(a \in Actions _{i}\), (1) \( local \left( \overline{ GActions }_{i}\right) = Actions _{i}\); (2) \( local \left( \overline{ GEvents }_{i}\right) = Events _{i}\); (3)
, and \(a \in Actions _{i}\), (1) \( local \left( \overline{ GActions }_{i}\right) = Actions _{i}\); (2) \( local \left( \overline{ GEvents }_{i}\right) = Events _{i}\); (3)  .
.
Recall that \( \overline{ GEvents }_{i}\cap \overline{ GEvents }_{j}=\varnothing \) for \(i\ne j\),

and  . While for correct haps, \( local \) provides a translation to local format on a hap-by-hap basis, the same cannot be extended to all haps because system events from \( SysEvents _{i}\) and byzantine actions
. While for correct haps, \( local \) provides a translation to local format on a hap-by-hap basis, the same cannot be extended to all haps because system events from \( SysEvents _{i}\) and byzantine actions  do not correspond to any local hap, to be recorded in i’s history. Thus, the localization function \(\sigma \) is defined on sets of global haps:
do not correspond to any local hap, to be recorded in i’s history. Thus, the localization function \(\sigma \) is defined on sets of global haps:
Definition 15
We define a localization function  :
:

Thus, as intended, for any \(E \in \overline{ GEvents }_{i}\), the local record left by \({\mathop { fake }\left( i,E\right) }\) for agent i is the same as the record of E, whereas for any \(A'\in \overline{ GActions }_{i}\) and any  , the local record of \({\mathop { fake }\left( i,A\mapsto A'\right) }\) for i is the same as that of \(A'\), whichever action A was taken in reality.
, the local record of \({\mathop { fake }\left( i,A\mapsto A'\right) }\) for i is the same as that of \(A'\), whichever action A was taken in reality.
Definition 16
We abbreviate  and
and  for a tuple of performed events \(X_\epsilon \subseteq GEvents _{}\) and actions \(X_i \subseteq \overline{ GActions }_{i}\) for each \(i \in \mathcal {A}\). Given a global state \( r_{}\left( t\right) = \bigl (r_{\epsilon }\left( t\right) , r_{1}\left( t\right) , \dots , r_{n}\left( t\right) \bigr ) \in \mathscr {G}\), we define agent i’s update function
for a tuple of performed events \(X_\epsilon \subseteq GEvents _{}\) and actions \(X_i \subseteq \overline{ GActions }_{i}\) for each \(i \in \mathcal {A}\). Given a global state \( r_{}\left( t\right) = \bigl (r_{\epsilon }\left( t\right) , r_{1}\left( t\right) , \dots , r_{n}\left( t\right) \bigr ) \in \mathscr {G}\), we define agent i’s update function  that outputs a new local state from \( {\mathscr {L}^{}_{i}} \) based on i’s actions \(X_i\) and events \(X_{\epsilon }\):
that outputs a new local state from \( {\mathscr {L}^{}_{i}} \) based on i’s actions \(X_i\) and events \(X_{\epsilon }\):

(note that, in transitional runs,  is always used after the action
is always used after the action  ; thus, in the absence of go(i), it is always the case that \(X_i = \varnothing \)). Similarly, the environment’s state update function
; thus, in the absence of go(i), it is always the case that \(X_i = \varnothing \)). Similarly, the environment’s state update function

outputs a new state of the environment based on events \(X_{\epsilon }\) and all actions \(X_i\):  Summarizing,
Summarizing,

The following properties directly follow from Definition 7 of the i-intervention  :
:
Lemma 17
Let  and r be an arbitrary run. Then
and r be an arbitrary run. Then
-
1.
 , i.e.,
, i.e.,  removes all actions.
removes all actions. -
2.
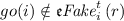 , i.e.,
, i.e.,  never lets agent i act.
never lets agent i act. -
3.
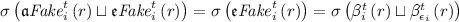 .
. -
4.
\(r_i(t+1) \ne r_i(t)\) iff
 .
.
The last two properties mean that from i’s local perspective, the intervention is imperceptible (also when agent i was unaware of the passing round in the given run).
Proof
(of Brain-in-a-Vat Lemma 8). Let  . Prop. 6 follows from the definitions of
. Prop. 6 follows from the definitions of  and
and  . Prop. 7 follows from (1). Prop. 8 follows from Lemma 17.1 for i and from the definitions of
. Prop. 7 follows from (1). Prop. 8 follows from Lemma 17.1 for i and from the definitions of  and
and  for \(j\ne i\). Prop. 5 follows from (1) for i and from the definition of
for \(j\ne i\). Prop. 5 follows from (1) for i and from the definition of  for \(j\in Byz\). Prop. 2–4 depend solely on rounds
for \(j\in Byz\). Prop. 2–4 depend solely on rounds  to
to  of \(r'\), whereas the transitionality of \(r'\) for Prop. 1 from round
of \(r'\), whereas the transitionality of \(r'\) for Prop. 1 from round  onward directly follows from Definition 6. We now show Prop. 1–4 for \(m\le t\) by induction on m.
onward directly follows from Definition 6. We now show Prop. 1–4 for \(m\le t\) by induction on m.
Base: \(m=0\). Prop. 3–4 and transitionality for Prop. 1 are trivial. Prop. 2 follows from Definition 6.
Step from m to \(m+1\) . We prove Prop. 1 based on the gullibility of i and delayability (and fallibility) of all other \(j\ne i\). In order to show that  , we need to demonstrate that the \(\beta \)-sets prescribed by \( adj \) can be obtained in a regular round. Since the adversary’s choice of actions
, we need to demonstrate that the \(\beta \)-sets prescribed by \( adj \) can be obtained in a regular round. Since the adversary’s choice of actions  for all \(j\in \mathcal {A}\) is immaterial due to the absence of go(j) (by Prop. 7 for i and Prop. 6 for other \(j\ne i\)), we concentrate on ensuring the adversary can choose suitable \(\alpha \)-sets of events. Consider
for all \(j\in \mathcal {A}\) is immaterial due to the absence of go(j) (by Prop. 7 for i and Prop. 6 for other \(j\ne i\)), we concentrate on ensuring the adversary can choose suitable \(\alpha \)-sets of events. Consider  from the original run r. The set
from the original run r. The set  is coherent because r is transitional. By the delayability of all \(j \ne i\),
is coherent because r is transitional. By the delayability of all \(j \ne i\),  Note that for any \(Z \subseteq FEvents _{i}\),
Note that for any \(Z \subseteq FEvents _{i}\),  because
because  . Thus, by the gullibility of i,
. Thus, by the gullibility of i,

(note that this set is coherent because it contains no correct events and neither go(i) nor \({\mathop { hibernate }\left( i\right) }\)). Finally, by the fallibility of all agents \(j\in Byz\),  This
This  is coherent and unaffected by filtering (there are no correct receives in
is coherent and unaffected by filtering (there are no correct receives in  to be filtered out, and only at most f agents from \(\{i\}\sqcup Byz\) become byzantine).
to be filtered out, and only at most f agents from \(\{i\}\sqcup Byz\) become byzantine).
It remains to show that filtering turns these sets  ,
,  into the exact \(\beta \)-sets prescribed by the adjustment \( adj \). Let us abbreviate:
into the exact \(\beta \)-sets prescribed by the adjustment \( adj \). Let us abbreviate:

Our goal is to show that  and
and  for each \(j \in \mathcal {A}\). After the filtering phase, for our i and \(j\ne i\), we have the following:
for each \(j \in \mathcal {A}\). After the filtering phase, for our i and \(j\ne i\), we have the following:

the latter being exactly  . Since \(go(j) \notin \varUpsilon \) for any \(j \in \mathcal {A}\), we also have that
. Since \(go(j) \notin \varUpsilon \) for any \(j \in \mathcal {A}\), we also have that  for all \(j \in \mathcal {A}\). This completes the induction step for Prop. 1.
for all \(j \in \mathcal {A}\). This completes the induction step for Prop. 1.
For Prop. 2, the induction step follows from Lemma 17.3–4. We have:
-
if
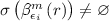 , then
, then  by IH. It remains to use Lemma 17.3 to see that the last expression is the same as
by IH. It remains to use Lemma 17.3 to see that the last expression is the same as 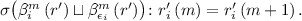
-
if
 but \(r_{i}\left( m+1\right) \ne r_{i}\left( m\right) \), then \( r_{i}\left( m+1\right) =\)
but \(r_{i}\left( m+1\right) \ne r_{i}\left( m\right) \), then \( r_{i}\left( m+1\right) =\)  by IH. By Lemma 17.4, we also have
by IH. By Lemma 17.4, we also have  . Thus, this case can be concluded by using Lemma 17.3 as it was done in the previous case.
. Thus, this case can be concluded by using Lemma 17.3 as it was done in the previous case. -
if
 and \(r_{i}\left( m+1\right) = r_{i}\left( m\right) \), then
and \(r_{i}\left( m+1\right) = r_{i}\left( m\right) \), then  by Lemma 17.3–4 (note that
by Lemma 17.3–4 (note that  , meaning that
, meaning that  ). Using IH, we now immediately get,
). Using IH, we now immediately get, 
This completes the proof of the induction step for Prop. 2.
For Prop. 3–4, the induction step is even simpler. Since, for any \(j \ne i,\)  by Prop. 6, it follows that
by Prop. 6, it follows that  by IH. Similarly,
by IH. Similarly,  by Prop. 6 for \(j \notin \{i\}\sqcup Byz\). Thus, being correct at m by IH, such agents j remain correct after round
by Prop. 6 for \(j \notin \{i\}\sqcup Byz\). Thus, being correct at m by IH, such agents j remain correct after round  . \(\square \)
. \(\square \)
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Kuznets, R., Prosperi, L., Schmid, U., Fruzsa, K. (2019). Epistemic Reasoning with Byzantine-Faulty Agents. In: Herzig, A., Popescu, A. (eds) Frontiers of Combining Systems. FroCoS 2019. Lecture Notes in Computer Science(), vol 11715. Springer, Cham. https://doi.org/10.1007/978-3-030-29007-8_15
Download citation
DOI: https://doi.org/10.1007/978-3-030-29007-8_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-29006-1
Online ISBN: 978-3-030-29007-8
eBook Packages: Computer ScienceComputer Science (R0)






 for byzantine sends or in
for byzantine sends or in 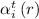 for correct ones that will be actually performed (see filtering stage 2).
for correct ones that will be actually performed (see filtering stage 2). and
and  are presented in Appendix in Definition
are presented in Appendix in Definition  ;
; .
. , i.e.,
, i.e.,  removes all actions.
removes all actions.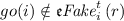 , i.e.,
, i.e.,  never lets agent i act.
never lets agent i act.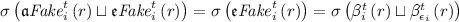 .
. .
.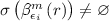 , then
, then  by IH. It remains to use Lemma
by IH. It remains to use Lemma 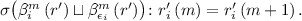
 but
but  by IH. By Lemma
by IH. By Lemma  . Thus, this case can be concluded by using Lemma
. Thus, this case can be concluded by using Lemma  and
and  by Lemma
by Lemma  , meaning that
, meaning that  ). Using IH, we now immediately get,
). Using IH, we now immediately get, 