Abstract
Refinement checking plays an important role in system verification. This means that the correctness of the system is established by showing a refinement relation between two models; one for the implementation and one for the specification. In [21], Wang et al. describe an algorithm based on antichains for efficiently deciding stable failures refinement and failures-divergences refinement. We identify several issues pertaining to the correctness and performance in these algorithms and propose new, correct, antichain-based algorithms. Using a number of experiments we show that our algorithms outperform the original ones in terms of running time and memory usage.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Refinement is often an integral part of a mature engineering methodology for designing a (software) system in a stepwise manner. It allows one to start from a high-level specification that describes the permitted and desired behaviours of a system and arrive at a detailed implementation that behaves as originally specified. While in many settings, refinement is often used rather informally, it forms the mathematical cornerstone in the theoretical development of the process algebra CSP (Communicating Sequential Processes) by Hoare [12, 17, 18].
This formal view on refinement—as a mathematical relation between a specification and its implementation—has been used successfully in industrial settings [10], and it has been incorporated in commercial Formal Model-Driven Engineering tools such as Dezyne [3]. In such settings there are a variety of refinement relations, each with their own properties. In particular, each notion of refinement offers specific guarantees on the (types of) behavioural properties of the specification that carry over to correct implementations. For the theory of CSP, the—arguably—most prominent refinement relations are stable failures refinement [2, 18] and failures-divergences refinement [18]. Both are implemented in the tool FDR [6] for specifying and analysing CSP processes.
Both stable failures refinement and failures-divergences refinement are computationally hard problems; deciding whether there is a refinement relation between an implementation and a specification, both represented by CSP processes or labelled transition systems, is PSPACE-hard [13]. In practice, however, tools such as FDR are able to work with quite large state spaces. The basic algorithm for deciding a stable failures refinement or a failures-divergences refinement between an implementation and a specification relies on a normalisation of the specification. This normalisation is achieved by a subset construction that is used to obtain a deterministic transition system which represents the specification.
As observed in [21] and inspired by successes reported, e.g., in [1], antichain techniques can be exploited to improve on the performance of refinement checking algorithms. Unfortunately, a closer inspection of the results and algorithms in [21], reveals several issues. First, the definitions of stable failures refinement and failures-divergences refinement used in [21] do not match the definitions of [2, 18], nor do they seem to match known relations from the literature [8].
Second, as we demonstrate in Example 2 in this paper, the results [21, Theorems 2 and 3] claiming correctness of their algorithms for deciding both refinement relations are incorrect. We do note that their algorithm for checking stable failures refinement correctly decides the refinement relation defined by [2, 18].
Third, unlike claimed by the authors in [21], their algorithms violate the antichain property as we demonstrate in Example 4. Fourth, their algorithms suffer from severely degraded performance due to suboptimal decisions made when designing the algorithms, leading to an overhead of a factor \(|\varSigma |\), where \(\varSigma \) is the set of events. When using a FIFO queue to realise a breadth-first search strategy instead of the stack used by default for a depth-first search this factor is even greater, viz. \(|\varSigma |^{|S|}\), where \(S\) is the set of states of the implementation, see our Example 3. Note that there are compelling reasons for using a breadth-first strategy [17]; e.g., the conciseness of counterexamples to refinement.
The contributions of the current paper are as follows. Apart from pointing out the issues in [21], we propose new antichain-based algorithms for deciding stable failures refinement and failures-divergences refinement and we prove their correctness. We compare the performance of the stable failures refinement algorithm of [21] to ours. Due to the flaw in their algorithm for checking failures-divergences refinement, a comparison for this refinement relation makes little sense. Our results indicate a small improvement in run time performance for practical models when using depth-first search, whereas our experiments using breadth-first search illustrate that decision problems intractable using the algorithm of [21] generally become quite easy using our algorithm.
The remainder of this paper is organised as follows. We recall the necessary mathematics in Sect. 2 and we describe the essence of refinement checking algorithms in Sect. 3. In Sect. 4, we analyse the algorithms of [21] and in Sect. 5, we propose new antichain-based refinement algorithms, claim their correctness and provide proof sketches. In Sect. 6, we compare the performance of our algorithm to that of [21]. Full proofs of our claims can be found in a technical report [14], which also contains additional experiments, showing that further speed improvements can be obtained by applying divergence-preserving branching bisimulation [7] minimisation before checking refinement.
2 Preliminaries
In this section the preliminaries of labelled transition systems, stable failures refinement and failures-divergences refinement checking are introduced.
2.1 Labelled Transition Systems
Let \(\varSigma \) be a finite set of event labels that does not contain the constant \(\tau \), modelling internal events.
Definition 1
A labelled transition system is a tuple \(\mathcal {L}= (S, \iota , \textit{Act}, \rightarrow )\) where \(S\) is a set of states; \(\iota \in S\) is an initial state; \(\textit{Act} = \varSigma \) or \(\textit{Act} = \varSigma \cup \{\tau \}\) is a set of actions and \(\rightarrow \,\subseteq S\times \textit{Act} \times S\) is a labelled transition relation.
The following definitions are in the context of a given labelled transition system \(\mathcal {L}= (S, \iota , \textit{Act}, \rightarrow )\). We typically use letters s, t, u to denote states, U, V to denote sets of states, a to denote an arbitrary action, e to denote an arbitrary event and \(\sigma , \rho \in \textit{Act} ^*\) to denote a sequence of actions.
We adopt the following conventions and notation. Whenever \((s, a, t) \in \mathop {\rightarrow {}}\), we write \(s \xrightarrow {a} t\); we write \(s \xrightarrow {a} {}\) just whenever there is some t such that \(s \xrightarrow {a} t\), and  holds iff not \(s \xrightarrow {a}\). The set of actions that can be executed in s is given by the set \(\mathsf {enabled}(s)\), defined as \(\mathsf {enabled}(s) = \{a \in \textit{Act} \mid s \xrightarrow {a} {} \}\). We generalise the relation \(\rightarrow \) in the usual manner to sequences of actions as follows:
holds iff not \(s \xrightarrow {a}\). The set of actions that can be executed in s is given by the set \(\mathsf {enabled}(s)\), defined as \(\mathsf {enabled}(s) = \{a \in \textit{Act} \mid s \xrightarrow {a} {} \}\). We generalise the relation \(\rightarrow \) in the usual manner to sequences of actions as follows:  holds iff \(s = t\), and
holds iff \(s = t\), and  holds iff there is some u such that \(s \xrightarrow {a} u\) and
holds iff there is some u such that \(s \xrightarrow {a} u\) and  . Finally, the weak transition relation
. Finally, the weak transition relation  is the least relation satisfying:
is the least relation satisfying:
-
 if there is some \(\sigma \in \tau ^*\) such that
if there is some \(\sigma \in \tau ^*\) such that  ,
, -
if \(s \xrightarrow {a} t\) then
 ,
, -
if
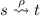 and
and 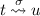 then
then 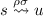 .
.
Definition 2
Traces, weak traces and reachable states are defined as follows:
-
\(\sigma \in \textit{Act} ^*\) is a trace starting in s iff
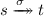 for some t. We denote the set of all traces starting in s by \(\mathsf {traces}(s)\), and we define \(\mathsf {traces}(\mathcal {L}) = \mathsf {traces}(\iota )\),
for some t. We denote the set of all traces starting in s by \(\mathsf {traces}(s)\), and we define \(\mathsf {traces}(\mathcal {L}) = \mathsf {traces}(\iota )\), -
\(\sigma \in \varSigma ^*\) is a weak trace starting in s iff
 for some t. The set of all weak traces starting in s is denoted by \(\mathsf {traces}_w(s)\), and we define \(\mathsf {traces}_w(\mathcal {L}) = \mathsf {traces}_w(\iota )\),
for some t. The set of all weak traces starting in s is denoted by \(\mathsf {traces}_w(s)\), and we define \(\mathsf {traces}_w(\mathcal {L}) = \mathsf {traces}_w(\iota )\), -
the set of states, reachable from s is defined as
 ; we define \(\mathsf {reachable}(\mathcal {L}) = \mathsf {reachable}(\iota )\).
; we define \(\mathsf {reachable}(\mathcal {L}) = \mathsf {reachable}(\iota )\).
The semantics of the CSP process algebra builds on observations of failures and divergences. A failure is a set of event labels that the system observably refuses following an experiment on that system, i.e., after executing a weak trace on that system.
By assumption, refusals can only be observed when the system has stabilised. Formally, a state s is stable, denoted \(\mathsf {stable}(s)\), if and only if  . A divergence can be understood as the potential inability of a system to stabilise. In effect, this means that a divergence is an infinite sequence of \(\tau \)-actions; formally, a state s is a diverging state, denoted \(\mathsf {div}(s)\), if and only if there is an infinite sequence of states \(s_i\) such that \(s \xrightarrow {\tau } s_1 \xrightarrow {\tau } s_2 \xrightarrow {\tau } \cdots \). For a set of states U, we write \(\mathsf {div}(U)\) iff \(\mathsf {div}(s)\) for some \(s \in U\).
. A divergence can be understood as the potential inability of a system to stabilise. In effect, this means that a divergence is an infinite sequence of \(\tau \)-actions; formally, a state s is a diverging state, denoted \(\mathsf {div}(s)\), if and only if there is an infinite sequence of states \(s_i\) such that \(s \xrightarrow {\tau } s_1 \xrightarrow {\tau } s_2 \xrightarrow {\tau } \cdots \). For a set of states U, we write \(\mathsf {div}(U)\) iff \(\mathsf {div}(s)\) for some \(s \in U\).
Definition 3
Let \(s \in S\) be a stable state. The refusals of s are defined asFootnote 1 the set \(\mathsf {refusals}(s) = \mathcal {P}(\varSigma \setminus \mathsf {enabled}(s))\). For a set of (not necessarily stable) states U, we define \(\mathsf {refusals}(U) = \{ X \subseteq \varSigma \mid \exists s \in U : \mathsf {stable}(s) \wedge X \in \mathsf {refusals}(s) \}\).
We are now in a position to formally define the set of divergences and the set of failures of an LTS; we here follow the standard conventions and definitions of [4, 9, 18]. Note that in [14] we instead have adopted the notational conventions of [21] to allow for an easier comparison of our results to theirs.
Definition 4
The set of all divergences of a state s, denoted by \(\mathsf {divergences}(s)\), is defined as  . We define \(\mathsf {divergences}(\mathcal {L}) = \mathsf {divergences}(\iota )\).
. We define \(\mathsf {divergences}(\mathcal {L}) = \mathsf {divergences}(\iota )\).
Observe that a divergence is not only a weak trace that can reach a diverging state, but also any suffix of a weak trace that can reach a diverging state. This is based on the assumption that divergences lead to chaos. In theories in which divergences are considered chaotic, such chaos obscures all information about the behaviours involving a diverging state; we refer to this as obscuring post-divergences details.
Definition 5
The set of all stable failures of a state s, denoted \(\mathsf {failures}(s)\), is defined as  . The set of stable failures of a state s with post-divergences details obscured, denoted \(\mathsf {failures}_\bot (s)\), is defined as \(\mathsf {failures}(s) \cup \{(\sigma , X) \in \varSigma ^* \times \mathcal {P}(\varSigma ) \mid \sigma \in \mathsf {divergences}(s) \}\).
. The set of stable failures of a state s with post-divergences details obscured, denoted \(\mathsf {failures}_\bot (s)\), is defined as \(\mathsf {failures}(s) \cup \{(\sigma , X) \in \varSigma ^* \times \mathcal {P}(\varSigma ) \mid \sigma \in \mathsf {divergences}(s) \}\).
The two standard models of CSP are the stable failures model and the failures-divergences model. The refinement relations on LTSs, induced by these models, are called the stable failures refinement and the failures-divergences refinement. We remark that the LTS that is refined is commonly referred to as the specification, whereas the LTS that refines the specification is often referred to as the implementation.
Definition 6
Let \(\mathcal {L}_1\) and \(\mathcal {L}_2\) be two LTSs. We say that \(\mathcal {L}_2\) is a stable failures refinement of \(\mathcal {L}_1\), denoted by \(\mathcal {L}_1 \mathrel {\sqsubseteq _{\text {sfr}}}\mathcal {L}_2\), iff \(\mathsf {traces}_w(\mathcal {L}_2) \subseteq \mathsf {traces}_w(\mathcal {L}_1)\) and \(\mathsf {failures}(\mathcal {L}_2) \subseteq \mathsf {failures}(\mathcal {L}_1)\). LTS \(\mathcal {L}_2\) is a failures-divergences refinement of \(\mathcal {L}_1\), denoted by \(\mathcal {L}_1 \mathrel {\sqsubseteq _{\text {fdr}}}\mathcal {L}_2\), iff \(\mathsf {failures}_\bot (\mathcal {L}_2) \subseteq \mathsf {failures}_\bot (\mathcal {L}_1)\) and \(\mathsf {divergences}(\mathcal {L}_2) \subseteq \mathsf {divergences}(\mathcal {L}_1)\).
Remark 1
The notions defined above appear in different formulations in [21]. Their stable failures refinement omits the clause for weak trace inclusion, and their failures-divergences refinement replaces \(\mathsf {failures}_\bot \) with \(\mathsf {failures}\). This yields refinement relations different from the standard ones and neither relation seems to appear in the literature [8].
We finish this section with a small example, illustrating the difference between failures-divergences refinement and stable failures refinement.
Example 1
Consider the two transition systems (named after their initial states \(s_0\) and \(t_0\)) depicted below.

Observe that we have \(s_0 \mathrel {\sqsubseteq _{\text {fdr}}}t_0\), but not \(s_0 \mathrel {\sqsubseteq _{\text {sfr}}}t_0\). The latter fails because aa is a trace of \(t_0\), but not of \(s_0\); the same goes for the stable failure \((a,\{b\})\) of \(t_0\). The failures-divergences refinement holds because the divergent trace a obfuscates the observations of traces of the form \(aa^+\): since divergence is chaos, anything is permitted. We do have \(t_0 \mathrel {\sqsubseteq _{\text {sfr}}}s_0\) but not \(t_0 \mathrel {\sqsubseteq _{\text {fdr}}}s_0\). The latter fails because of the divergent trace a not being present in \(t_0\). Stable failures refinement holds because all traces and stable failure pairs of \(s_0\) are included in those of \(t_0\); in particular, the instability of state \(s_1\) causes \(s_1\) not to contribute to the stable failures set of \(s_0\). \(\square \)
3 Refinement Checking
In general, the set of failures and divergences of an LTS can be infinite. Therefore, checking inclusion of the set of failures or divergences is not viable. In [17, 18], an algorithm to decide refinement between two labelled transition systems is sketched. As a preprocessing to this algorithm, all diverging states in both LTSs are marked. The algorithm then relies on exploring the cartesian product of the normal form representation of the specification, i.e., the LTS that is to be refined, and the implementation. We remark that what we refer to as cartesian product, defined in [17], is called a synchronous product in [21]. For each pair in the product it checks whether it can locally decide non-refinement of the implementation state with the normal form state. A pair for which non-refinement holds is referred to as a witness.
Following [18, 21] and specifically the terminology of [17], we formalise the cartesian product between LTSs that is explored by the procedure.
Definition 7
Let \(\mathcal {L}_1 = (S_1, \iota _1, \varSigma , \rightarrow _1)\) and \(\mathcal {L}_2 = (S_2, \iota _2, \textit{Act}, \rightarrow _2)\) be LTSs. The cartesian product of \(\mathcal {L}_1\) and \(\mathcal {L}_2\) is the LTS \(\mathcal {L}_1 \times \mathcal {L}_2 = (S, \iota , \textit{Act}, \rightarrow )\) satisfying \(S= S_1 \times S_2\); \(\iota = (\iota _1, \iota _2)\); and the transition relation \(\rightarrow \) is the smallest relation satisfying the following conditions for all \(s_1,t_1 \in S_1\), and \(s_2,t_2 \in S_2\) and \(e \in \varSigma \):
-
If \(s_2 \xrightarrow {\tau }_2 t_2\) then \((s_1, s_2) \xrightarrow {\tau } (s_1, t_2)\),
-
If \(s_1 \xrightarrow {e}_1 t_1\) and \(s_2 \xrightarrow {e}_2 t_2\) then \((s_1, s_2) \xrightarrow {e} (t_1, t_2)\).
We remark that \(\varSigma \) is used in \(\mathcal {L}_1\) to indicate that it has no transitions labelled with \(\tau \), whereas, \(\mathcal {L}_2\) might contain \(\tau \)-transitions. A key property of the cartesian product, provable by induction on the length of sequence \(\sigma \), is the following:
Proposition 1
Let \(\mathcal {L}_1 = (S_1, \iota _1, \varSigma , \rightarrow _1)\) and \(\mathcal {L}_2 = (S_2, \iota _2, \textit{Act}, \rightarrow _2)\) be LTSs, and let \(\mathcal {L}_1 \times \mathcal {L}_2 = (S,\iota ,\textit{Act},\rightarrow )\) be their cartesian product. For all \(s_1 \in S_1\), \(s_2 \in S_2\) and all  ,
,  iff
iff  and
and  .
.
The normal form LTS is obtained using a typical subset construction as is common when determinising a transition system. Although all states in an LTS in normal form are stable, the states of the original LTS comprising a normal form state may not be. To avoid confusion when we wish to reason about the stability and divergences of states U in the LTS \(\mathcal {L}\) underlying a normal form LTS, rather than the state of the normal form LTS, we write \([\![U]\!]_\mathcal {L}\) to indicate we refer to the set of states in \(\mathcal {L}\). Stable failures refinement and failures-divergences refinement require different normal forms.
Definition 8
Let \(\mathcal {L}= (S,\iota ,\textit{Act},\rightarrow )\) be a labelled transition system. Set \(S' = \mathcal {P}(S)\),  . The stable failures refinement normal form of \(\mathcal {L}\) is the LTS \(\mathsf {norm}_\text {sfr}(\mathcal {L}) =(S', \iota ', \varSigma , \rightarrow ')\), where \(\rightarrow '\) is defined as \(U \xrightarrow {~e}{\!\!}'\, V\) if and only if
. The stable failures refinement normal form of \(\mathcal {L}\) is the LTS \(\mathsf {norm}_\text {sfr}(\mathcal {L}) =(S', \iota ', \varSigma , \rightarrow ')\), where \(\rightarrow '\) is defined as \(U \xrightarrow {~e}{\!\!}'\, V\) if and only if  for all \(U, V \subseteq S\) and \(e \in \varSigma \). The failures-divergences refinement normal form of \(\mathcal {L}\) is the LTS \(\mathsf {norm}_\text {fdr}(\mathcal {L}) = (S',\iota ',\varSigma , \rightarrow '')\) where \(\rightarrow ''\) is defined as \(U \xrightarrow {~e}{\!\!}''\, V\) if and only if \(U \xrightarrow {~e}{\!\!}'\, V\) and not \(\mathsf {div}([\![U]\!]_\mathcal {L})\).
for all \(U, V \subseteq S\) and \(e \in \varSigma \). The failures-divergences refinement normal form of \(\mathcal {L}\) is the LTS \(\mathsf {norm}_\text {fdr}(\mathcal {L}) = (S',\iota ',\varSigma , \rightarrow '')\) where \(\rightarrow ''\) is defined as \(U \xrightarrow {~e}{\!\!}''\, V\) if and only if \(U \xrightarrow {~e}{\!\!}'\, V\) and not \(\mathsf {div}([\![U]\!]_\mathcal {L})\).
We remark that we deliberately permit the empty set to be a state in a normal form LTS. Clearly, a normal form LTS satisfies \(\emptyset \xrightarrow {e} \emptyset \) for all actions e. Moreover, note that a normal form LTS is deterministic; in particular, for all \(\sigma \), and states U, T, V of a normal form LTS  and
and  implies \(T = V\).
implies \(T = V\).
The structure explored by the refinement checking procedure of [17, 18] is essentially the cartesian product \(\mathsf {norm}_\text {sfr}(\mathcal {L}_1) \times \mathcal {L}_2\) in case of stable failures refinement, or \(\mathsf {norm}_\text {fdr}(\mathcal {L}_1) \times \mathcal {L}_2\) in case of failures-divergences refinement. For these structures the related witnesses, where the reachability of such a witness indicates non-refinement, are then as follows:
Definition 9
Let \(\mathcal {L}_1\) and \(\mathcal {L}_2\) be LTSs.
-
A state (U, s) in \(\mathsf {norm}_\text {sfr}(\mathcal {L}_1) \times \mathcal {L}_2\) is called an SFR-witness iff \(U = \emptyset \); or \(\mathsf {stable}(s)\) and not \(\mathsf {refusals}(s) \subseteq \mathsf {refusals}([\![U]\!]_{\mathcal {L}_1})\),
-
a state (U, s) in \(\mathsf {norm}_\text {fdr}(\mathcal {L}_1) \times \mathcal {L}_2\) is called an FDR-witness iff not \(\mathsf {div}([\![U]\!]_{\mathcal {L}_1})\), and either \(\mathsf {div}(s)\); or \(U = \emptyset \); or \(\mathsf {stable}(s)\) and not \(\mathsf {refusals}(s) \subseteq \mathsf {refusals}([\![U]\!]_{\mathcal {L}_1})\).
The following statement formalises the insights of [17]; both results follow from Proposition 1 and the characteristics of the normal form LTSs.
Theorem 1
Let \(\mathcal {L}_1\) and \(\mathcal {L}_2\) be LTSs. Then:
-
\(\mathcal {L}_1 \mathrel {\sqsubseteq _{\text {sfr}}}\mathcal {L}_2\) iff no SFR-witness is reachable in \(\mathsf {norm}_\text {sfr}(\mathcal {L}_1) \times \mathcal {L}_2\),
-
\(\mathcal {L}_1 \mathrel {\sqsubseteq _{\text {fdr}}}\mathcal {L}_2\) iff no FDR-witness is reachable in \(\mathsf {norm}_\text {fdr}(\mathcal {L}_1) \times \mathcal {L}_2\).
4 Antichain Algorithms for Refinement Checking
The normalisation of the specification LTS in refinement checking dominates the theoretical worst-case run time complexity of refinement checking, which itself is a PSPACE-hard problem. In practice, however, refinement checking can often be done quite effectively. Nevertheless, as observed in [21], there is room for improvement by exploiting an antichain approach to keep the size of the normal form LTS of the specification in check.
An antichain is a set \(\mathcal {A} \subseteq X\) of a partially ordered set \((X,\le )\) in which all distinct \(x,y \in \mathcal {A}\) are incomparable: neither \(x \le y\) nor \(y \le x\). Given a partially ordered set \((X,\le )\) and an antichain \(\mathcal {A}\), the operation \(\Subset \) checks whether \(\mathcal {A}\) ‘contains’ an element x; that is, \(x \Subset \mathcal {A}\) holds true if and only if there is some \(y \in \mathcal {A}\) such that \(y \le x\). We write \(Y \Subset ^\forall \mathcal {A}\) iff \(y \Subset \mathcal {A}\) for all \(y \in Y\). Antichain \(\mathcal {A}\) can be extended by inserting an element \(x \in X\), denoted \(\mathcal {A} \Cup x\), which is defined as the set \(\{ y \mid y = x \vee (y \in \mathcal {A} \wedge x \not \le y)\}\). Note that this operation only yields an antichain whenever  .
.
As [1, 21] suggest, the state space of the cartesian product \((S,\iota ,\textit{Act},\rightarrow )\) between the normal form of LTS \(\mathcal {L}_1\) and the LTS \(\mathcal {L}_2\) induces a partially ordered set as follows. For \((U,s),(V,t) \in S\), define \((U,s) \le (V,t)\) iff \(s = t\) and \([\![U]\!]_{\mathcal {L}_1} \subseteq [\![V]\!]_{\mathcal {L}_1}\). Then the set \((S,\le )\) is a partially ordered set. The fundamental property underlying the reason why an antichain approach to refinement checking works is expressed by the following proposition, stating that the traces of any state (V, s) in the cartesian product can be executed from all states smaller than (V, s). We remark that this is due to including the empty set as a state in the normal form LTS.
Proposition 2
For all \((U,s) \le (V,s)\) of a normal form LTS \(\mathsf {norm}_\text {sfr}(\mathcal {L}_1) \times \mathcal {L}_2\) or \(\mathsf {norm}_\text {fdr}(\mathcal {L}_1) \times \mathcal {L}_2\) and for every sequence \(\sigma \in \textit{Act} ^*\) such that  , there is some \((U',t)\) such that
, there is some \((U',t)\) such that  and \((U',t) \le (V',t)\).
and \((U',t) \le (V',t)\).
The proof of this proposition proceeds by induction on the length of \(\sigma \) and is routine.
The main idea of the antichain algorithm is now as follows: the set of states of the cartesian product explored is recorded in an antichain. Whenever a new state of the cartesian product is found that is already included in the antichain (w.r.t. the membership test \(\Subset \)), further exploration of that state is unnecessary, thereby pruning the state space of the cartesian product. Note that it is not immediate that doing so is also ‘safe’ for refusals and divergences. Algorithm 1 is the pseudocode for checking stable failures refinement and failures-divergences refinement as presented in [21, Algorithms 2 and 3]; we remark that we combined these algorithms, as their check for failures-divergences refinement only requires an additional check for divergences (enabled by the Boolean \( CheckDiv \)).

Let us first stress that the algorithm correctly decides stable failures refinement but it fails to correctly decide failures-divergences refinement. Second, the algorithm also fails to decide the non-standard relations used in [21], see also Remark 1. All three issues are illustrated by the example below.
Example 2
Consider the four transition systems depicted below.

Let us first observe that the algorithm correctly decides that \(s_1 \mathrel {\sqsubseteq _{\text {sfr}}}s_0\) does not hold, which follows from a violation of \(\mathsf {traces}_w(s_0) \subseteq \mathsf {traces}_w(s_1)\). Next, observe that we have \(s_0 \mathrel {\sqsubseteq _{\text {fdr}}}s_1\), since the divergence of the root state \(s_0\) implies chaotic behaviour of \(s_0\) and, hence, any system refines such a system. However, Algorithm 1 returns false when CheckDiv holds.
With respect to the refinement relations defined in [21], we observe the following. Since \(s_0\) is not stable, we have \(\mathsf {failures}(s_0) = \emptyset \) and hence \(\mathsf {failures}(s_0) \subseteq \mathsf {failures}(s_1)\). Consequently, stable failures refinement as defined in [21] should hold, but as we already concluded above, the algorithm returns false when checking for \(s_1 \mathrel {\sqsubseteq _{\text {sfr}}}s_0\). Next, observe that the algorithm returns true when checking for \(s_2 \mathrel {\sqsubseteq _{\text {fdr}}}s_3\). The reason is that for the pair \((\{s_2\},s_3)\), it detects that state \(s_3\) diverges and concludes that since also the normal form state of the specification \(\{s_2\}\) diverges, it can terminate the iteration and return true. This is a consequence of splitting the divergence tests over two if-statements in lines 7 and 8. According to the failures-divergences refinement of [21], however, the algorithm should return false, since \(\mathsf {failures}(s_3) \subseteq \mathsf {failures}(s_2)\) fails to hold: we have \((a, \{a\}) \in \mathsf {failures}(s_3)\) but not \((a,\{a\}) \in \mathsf {failures}(s_2)\). \(\square \)
We note that the algorithm explores the cartesian product between the normal form of a specification, and an implementation in a depth-first, on-the-fly manner. While depth-first search is typically used for detecting divergences, [17] states a number of reasons for running the refinement check in a breadth-first manner. A compelling argument in favour of using a breadth-first search is conciseness of the counterexample in case of a non-refinement.
Algorithm 1 can be made to run in a breadth-first fashion simply by using a FIFO queue rather than a stack as the data structure for \( working \). However, our implementation of this algorithm suffers from a severely degraded performance. We can trace this back to the following three additional problems in the original algorithm, which also are present (albeit less pronounced in practice) when utilising a depth-first exploration:
-
1.
The refusal check on line 11 is also performed for unstable states, which, combined with the definition of \(\mathsf {refusals}\) in [21] (see also our remark in Footnote 1 on page 4), results in a repeated, potentially expensive, search for stable states;
-
2.
Adding the pair \((\textit{spec}, \textit{impl})\) that is taken from \( working \) to \( antichain \) might result in duplicate pairs in \( working \) since \( working \) is filled with all successors of that pair in line 21, regardless of whether these pairs are already scheduled for exploration, i.e., included in \( working \), or not;
-
3.
Contrary to the explicit claim in [21, Section 2.2], the set \( antichain \) is not guaranteed to be an antichain.
The first problem is readily seen to lead to undesirable overhead. The second and third problem are more subtle. We first illustrate the second problem: the following pathological example shows that the algorithm stores an excessive number of pairs in \( working \).
Example 3
Consider the family of LTSs \(\mathcal {L}_n^k = (S_n, \iota _n, \textit{Act} _{k},\rightarrow _n)\) with states \(S_n = \{s_1, \dots , s_n\}\), event labels \(\textit{Act} _{k} = \{e_1, \dots , e_k\}\) and transitions \(s_i \xrightarrow {e_j}_n s_{i-1}\) for all \(1 \le j \le k\), \(1 < i \le n\) and \(\iota _n = s_n\); see also the transition system depicted below. Note that each LTS that belongs to this family is completely deterministic.

Suppose one checks for refinement between an implementation and specification both of which are given by \(\mathcal {L}_n^k\); i.e., we test for \(\mathcal {L}_n^k \mathrel {\sqsubseteq _{\text {sfr}}}\mathcal {L}_n^k\). Then the stack \( working \) will contain exactly \(i {\cdot } (k{-}1) {+} 1\) pairs at the end of the i-th iteration (when \(i \le n\)), resulting in a working stack size of \(\mathcal {O}(n {\cdot } k)\) entries. At the end of the n-th iteration \( antichain \) contains all reachable pairs of the cartesian product, i.e., \( antichain = \{(\{s_j\},s_j) \mid 1 \le j \le n \}\) at that point. Emptying \( working \) after the n-th iteration will involve k antichain membership tests per entry. Consequently, \(\mathcal {O}(n {\cdot } k^2)\) antichain membership tests are required. A breadth-first search strategy requires even more antichain membership tests, viz., \(\mathcal {O}(k^n)\). \(\square \)
The example below illustrates the third problem of the algorithm, viz., the violation of the antichain property.
Example 4
Consider the two left-most labelled transition systems depicted below, along with the (normal form) cartesian product (the LTS on the right).

Algorithm 1 starts with \( working \) containing pair \((\{t_0\},s_0)\) and \( antichain = \emptyset \). Inside the loop, the pair \((\{t_0\},s_0)\) is popped from \( working \) and added to \( antichain \). The successors of the pair \((\{t_0\},s_0)\) are the pairs \((\{t_1\},s_1)\) and \((\{t_1, t_2\},s_1)\). Since \( antichain \) contains neither of these, both successors are added to \( working \) in line 21. Next, popping \((\{t_1\},s_1)\) from \( working \) and adding this pair to \( antichain \) results in \( antichain \) consisting of the set \(\{(\{t_0\},s_0), ( \{t_1\},s_1)\}\). In the final iteration of the algorithm, the pair \((\{t_1, t_2\},s_1)\) is popped from \( working \) and added to \( antichain \), resulting in the set \(\{(\{t_0\},s_0), (\{t_1\},s_1), (\{t_1, t_2\},s_1)\}\). Clearly, since \((\{t_1\},s_1) \le ( \{t_1, t_2\},s_1)\), the set \( antichain \) no longer is a proper antichain. \(\square \)
5 A Correct and Improved Antichain Algorithm
We address the identified performance problems by rearranging the computations that are conducted. Note that in order to solve the first performance problem, we only perform the check to compare the refusals of the implementation and the normal form state of the specification in case the implementation state is stable.
Solving the second performance problem is more involved. The essential observation here is that in order for the information in \( antichain \) to be most effective, states of the cartesian product must be added to \( antichain \) as soon as these are discovered, even if these have not yet been fully explored. This is achieved by maintaining, as an invariant, that \( working \Subset ^\forall antichain \); the states in \( working \) then essentially compose the frontier of the exploration. We achieve this by initialising \( working \) and \( antichain \) to consist of exactly the initial state of the cartesian product, and by extending \( antichain \) with all (not already discovered) successors for the state \((\textit{spec},\textit{impl})\) that is popped from \( working \). As a side effect, this also resolves the third issue, as now both \( working \) and \( antichain \) are only extended with states that have not yet been discovered, i.e., for which the membership test in \( antichain \) fails, and for which insertion with such states does not invalidate the antichain property.

Algorithm 2 shows the corrected antichain procedure for checking stable failures refinement and failures-divergences refinement. Since the algorithm fundamentally differs (in the relations that it computes) from the one in [21], we cannot reuse their arguments in our proof of correctness, which are based on invariants that do not hold in our case.
In the remainder of this section, we sketch the proof of correctness of Algorithm 2 as claimed below by Theorem 2. We focus on the proof of correctness w.r.t. failures-divergences refinement; for stable failures refinement the proof is almost the same except that it does not have to consider divergences.
Theorem 2
Let \(\mathcal {L}_i = (S_i, \iota _i, \textit{Act} _i, \rightarrow _i)\) where \(i \in \{1, 2\}\) be two labelled transition systems. Then:
-
\(\textsc {refines}_\text {new}(\mathcal {L}_1,\mathcal {L}_2,\text {false})\) returns true if and only if \(\mathcal {L}_1 \mathrel {\sqsubseteq _{\text {sfr}}}\mathcal {L}_2\);
-
\(\textsc {refines}_\text {new}(\mathcal {L}_1,\mathcal {L}_2,\text {true})\) returns true if and only if \(\mathcal {L}_1 \mathrel {\sqsubseteq _{\text {fdr}}}\mathcal {L}_2\);
For the remainder of this section we fix the two LTSs \(\mathcal {L}_i = (S_i, \iota _i, \textit{Act} _i, \rightarrow _i)\) where \(i \in \{1, 2\}\). First we show termination of Algorithm 2. A crucial observation of the antichain operations is that adding elements to an antichain does not affect the membership test of elements already included; see the lemma below.
Lemma 1
Let \((X,\le )\) be a partially ordered set, \(\mathcal {A} \subseteq X\) an antichain, and let \(x,y \in X\). If \(x \Subset \mathcal {A}\) and  then \(x \Subset (\mathcal {A} \Cup y)\).
then \(x \Subset (\mathcal {A} \Cup y)\).
Termination now follows from the observation that all states of the cartesian product that have been processed occur in \( antichain \) and do not get added back to \( working \); for this we rely on Lemma 1. To reason formally about the states that have been processed, we introduce a ghost variable \(\textit{done} \); i.e., \(\textit{done} \) is intialised as the empty set and each pair \((\textit{spec},\textit{impl})\) that is popped from \( working \) in line 5 is added to \(\textit{done} \) after line 22. We have the following invariants.
Lemma 2
Let \(\mathcal {L}_n = \mathsf {norm}_\text {fdr}(\mathcal {L}_1)\) if CheckDiv holds and \(\mathcal {L}_n = \mathsf {norm}_\text {sfr}(\mathcal {L}_1)\) otherwise. The while loop (lines 4–22) of Algorithm 2 satisfies the following invariants: \(\textit{done} \cup working \subseteq \mathsf {reachable}(\mathcal {L}_n \times \mathcal {L}_2)\), \(\textit{done} \, \cap \, working = \emptyset \), \(\textit{done} \cup working \Subset ^\forall antichain \) and \( working \) contains no duplicates.
Theorem 3
Algorithm 2 terminates for finite state, finitely branching LTSs.
Proof
The total number of pairs present in \(\mathsf {norm}_\text {sfr}(\mathcal {L}_1) \times \mathcal {L}_2\) and \(\mathsf {norm}_\text {fdr}(\mathcal {L}_1) \times \mathcal {L}_2\) are finite since \(\mathcal {L}_1\) and \(\mathcal {L}_2\) are finite state. By Lemma 2 we find that, when not CheckDiv, \( working \cup \textit{done} \subseteq \mathsf {reachable}(\mathsf {norm}_\text {sfr}(\mathcal {L}_1) \times \mathcal {L}_2)\). Likewise, we conclude \( working \cup \textit{done} \subseteq \mathsf {reachable}(\mathsf {norm}_\text {fdr}(\mathcal {L}_1) \times \mathcal {L}_2)\) when CheckDiv. Furthermore, as \(\textit{done} \cap working = \emptyset \), \(\textit{done} \) strictly increases in size each iteration and so only a finite number of iterations of the outer for-loop are possible. Termination of the inner for-loop follows from the assumption that \(\mathcal {L}_1\) and \(\mathcal {L}_2\) are finitely branching. \(\square \)
The correctness of the algorithm requires a lemma that shows anti-monotonicity of witnesses (cf. Definition 9); see below. Combined with Proposition 2 (see page 7) this allows us to conclude that the distance (defined below) from a state in the cartesian product to a witness is at least the distance to a witness from smaller states.
Lemma 3
Let (U, s), (V, s) be states of \(\mathsf {norm}_\text {sfr}(\mathcal {L}_1)\times \mathcal {L}_2\) satisfying \((U,s) \le (V,s)\). If (V, s) is an SFR-witness then (U, s) is an SFR-witness. Likewise, if (V, s) is an FDR-witness in \(\mathsf {norm}_\text {fdr}(\mathcal {L}_1)\times \mathcal {L}_2\) and \((U,s) \le (V,s)\) then (U, s) is an FDR-witness.
For a set of states \(\mathcal {U}\) in the cartesian product, let \(\textit{SFR}(\mathcal {U})\) be a predicate that is true if and only if \(\mathcal {U}\) contains an SFR-witness; likewise, \(\textit{FDR}(\mathcal {U})\) holds if and only if \(\mathcal {U}\) contains an FDR-witness. We denote the set of all reachable SFR-witnesses in the cartesian product \(\mathsf {norm}_\text {sfr}(\mathcal {L}_1) \times \mathcal {L}_2\) by \(\mathcal {S}\), and the set of all reachable FDR-witnesses in \(\mathsf {norm}_\text {fdr}(\mathcal {L}_1) \times \mathcal {L}_2\) by \(\mathcal {F}\). For a state (U, s) in the cartesian product, we define the distance to a set \(\mathcal {U}\) of the cartesian product by \(\textit{Dist}_{\,\mathcal {U}}(U,s)\) as the shortest distance from state (U, s) to a state in \(\mathcal {U}\). If \(\mathcal {U}\) is unreachable, the distance is set to infinity. Formally,  . We generalise this to a set of states \(\mathcal {V}\) as follows: \(\textit{Dist}_{\,\mathcal {U}}(\mathcal {V}) = \min \{\textit{Dist}_{\,\mathcal {U}}(U,s) \mid (U,s) \in \mathcal {V} \}\).
. We generalise this to a set of states \(\mathcal {V}\) as follows: \(\textit{Dist}_{\,\mathcal {U}}(\mathcal {V}) = \min \{\textit{Dist}_{\,\mathcal {U}}(U,s) \mid (U,s) \in \mathcal {V} \}\).
Proposition 3
For (U, s), (V, s) in \(\mathsf {norm}_\text {sfr}(\mathcal {L}_1)\times \mathcal {L}_2\) satisfying \((U,s) \le (V,s)\) we have \(\textit{Dist}_{\,\mathcal {S}}(U,s) \le \textit{Dist}_{\,\mathcal {S}}(V,s)\). Likewise, for (U, s), (V, s) in \(\mathsf {norm}_\text {fdr}(\mathcal {L}_1)\times \mathcal {L}_2\) satisfying \((U,s) \le (V,s)\) we have \(\textit{Dist}_{\,\mathcal {F}}(U,s) \le \textit{Dist}_{\,\mathcal {F}}(V,s)\).
Proof
Follows from Lemma 3 and Proposition 2. \(\square \)
We conclude with a sketch of the proof of correctness of the algorithm. The full proof can be found in [14].
Proof
(Theorem 2). We prove both implications, by contraposition, for the case of failures-divergences refinement. The proof of correctness for stable failures refinement proceeds along the same lines.
-
Assume that Algorithm 2 returns false. This occurs when the pair \((\textit{spec}, \textit{impl})\) satisfies the conditions of an FDR-witness, as follows from lines 7, 11 and 18 of Algorithm 2. Since \( working \subseteq \mathsf {reachable}(\mathsf {norm}_\text {fdr}(\mathcal {L}_1) \times \mathcal {L}_2)\) and \((\textit{spec},\textit{impl}) \in working \), the FDR-witness is reachable. By Theorem 1 we find that \(\mathcal {L}_1 \mathrel {\sqsubseteq _{\text {fdr}}}\mathcal {L}_2\) fails to hold.
-
Assume that an FDR-witness is reachable in \(\mathsf {norm}_\text {fdr}(\mathcal {L}_1) \times \mathcal {L}_2\), i.e., \(\mathcal {F} \ne \emptyset \). Then the following invariant holds in the while loop (lines 4–22):
$$\textit{Dist}_{\,\mathcal {F}}(\textit{done}) > \textit{Dist}_{\,\mathcal {F}}( working ) \text { and } \textit{Dist}_{\,\mathcal {F}}( working ) = \textit{Dist}_{\,\mathcal {F}}( antichain ). $$Towards a contradiction, assume Algorithm 2 returns true. This can only be the case when \( working \) is empty. Upon termination of the while loop, \(\textit{Dist}_{\,\mathcal {F}}( working ) = \textit{Dist}_{\,\mathcal {F}}(\emptyset ) = \infty \). By the above invariants, \(\textit{Dist}_{\,\mathcal {F}}( working ) = \textit{Dist}_{\,\mathcal {F}}( antichain )\). Since
 and \(\textit{Dist}_{\,\mathcal {F}}(\iota ) < \infty \), we also have \(\textit{Dist}_{\,\mathcal {F}}( antichain ) < \infty \). Contradiction. \(\square \)
and \(\textit{Dist}_{\,\mathcal {F}}(\iota ) < \infty \), we also have \(\textit{Dist}_{\,\mathcal {F}}( antichain ) < \infty \). Contradiction. \(\square \)
We remark that the correctness of the algorithm is independent of the search order that is used. That is, replacing the data structure for \( working \) with a FIFO queue results in a breadth-first search strategy and does not impair the correctness of the algorithm. As explained in [17], breadth-first search has the advantage to yield the shortest possible counterexamples. Reconstructing such counterexamples can be done efficiently by recording, for each state stored in \( working \), its breadth-first search level. We close this section by briefly returning to Example 3.
Example 5
Reconsider the family of transition systems of Example 3. Contrary to the original algorithm, the improved algorithm will, in each iteration, only add a single successor state to \( working \), because every other successor will already be part of \( antichain \). This results in \( working \) containing \(\mathcal {O}(1)\) entries; \( antichain \) will be queried \(\mathcal {O}(n{\cdot }k)\) times. Compared to the original algorithm, this reduces overhead for the depth-first search strategy by a factor \(n{\cdot }k\) in the working stack size and by a factor k in the number of antichain checks. For the breadth-first search strategy, the \( working \) size is reduced by a factor \(k^n\) and the \( antichain \) checks by a factor \(k^n/n\). \(\square \)
6 Experimental Validation
We have conducted several benchmarks to compare the run time of both algorithms to show that solving the identified issues actually improves the run time performance in practice.
For this purpose we have implemented a depth-first and breadth-first variant of both Algorithms 1 and 2 in a branch of the mCRL2Footnote 2 tool set [5] as part of the ltscompare tool, which is implemented in C++. The implementation of the \( working \) and \( antichain \) operations are the same. For the implementation of \(\mathsf {refusals}\) in Algorithm 1 we follow the definition of [21] (see also Footnote 1 on page 4), implementing refusals for any state, whereas for Algorithm 2 we follow Definition 3. The source modifications and experiments can be obtained from the downloadable package [15].
The experiments we consider are taken from three sources. First, Example 3 for exposing the performance overhead of the original algorithm. Second, several linearisability tests of concurrent data structures for more practical benchmarks. These models have been taken from [16], and consist of six implementations of concurrent data types that, when trace-refining their specifications, are guaranteed to be linearisable. As in [21], we approximate trace-refinement by the stronger stable failures refinement. For these models, the implementation and specification pairs are based on the same descriptions; the difference between the two is that the specification uses a simple construct to guarantee that each method of the concurrent data structure executes atomically. This significantly reduces the non-determinism and the number of transitions in the specification models.
Finally, an industrial model of a control system modelled in the Dezyne language [3] that first exposed the performance issues in practice. The industrial example is of a more traditional flavour in which the specification is an abstract description of the behaviours at the external interface of a control system, and the implementation is a detailed model that interacts with underlying services to implement the expected interface. For reasons of confidentiality, the industrial model cannot be made available.
All measurements have been performed on a machine with an Intel Core i7-7700HQ CPU 2.80 Ghz and a 16 GiB memory limit imposed by ulimit -Sv 16777216.
6.1 Benchmarking Example 3
Example 3 has been benchmarked for all combinations of \(k,n \le 500\), where k and n are multiples of 10, checking stable failures refinement between equivalent LTSs, i.e., \(\mathcal {L}^k_n \mathrel {\sqsubseteq _{\text {sfr}}}\mathcal {L}^k_n\). Figure 1 shows the run time performance (in seconds) of the depth-first variant of Algorithm 1 on the left and Algorithm 2 on the right.
The plots match the asymptotic growth as stated in Example 3, illustrating a factor k speed-up of our algorithm compared to the original one. A comparison of the performance of breadth-first search is infeasible as the original algorithm already runs into the memory limit for small k and n, whereas for Algorithm 2 there is only little difference between the depth-first and breadth-first variants.
Note that due to the absence of \(\tau \)-transitions, there is no performance difference in the computation of \(\mathsf {refusals}\) in both algorithms. Consequently, the difference in performance is entirely due to the different way of inspecting and extending \( working \).
The run time performance (in seconds) of Example 3 for depth-first search (left: original algorithm, right: our improved algorithm).
6.2 Benchmarking Practical Examples
Our next batch of experiments consists of more typical refinement checks, assessing whether the behaviours of the implementations are in line with the behaviours prescribed by their specifications. Characteristics of the state spaces are listed in Table 1.
The run time performance of both algorithms (both depth-first and breadth-first) can be found in Table 2. The run times we report are averages obtained from five runs. As illustrated by the figures in that table, we see small improvements of our algorithm over the original algorithm for depth-first search, whereas the improvements for breadth-first search are dramatic.
To better understand the reason behind the performance gains we obtain, we report on the maximal size of \( working \) and \( antichain \), and the number of successful and unsuccessful antichain membership tests; see Table 3. We only report on metrics for the breadth-first search strategy; the figures for the depth-first search strategy for both algorithms are similar; see [14].
For the breadth-first search strategy, the fact that the original algorithm delays adding state pairs to the antichain induces an enormous overhead in the size of \( working \) due to the many failing antichain checks. This can be seen from the large size of \( working \) and the small size of \( antichain \). Because of these differences in size, most antichain membership tests fail in the original algorithm. The situation is largely reversed in our improved algorithm, explaining the substantial performance improvements we observe. Since the original algorithm for failures-divergences refinement is incorrect, we only compared the performance of both algorithms for stable failures refinement. The performance of our failures-divergences refinement algorithm is comparable to our stable failures refinement algorithm; we refer to [14] for further details. In [14], we also performed additional experiments which show that further run time improvements can be obtained by applying divergence-preserving branching bisimulation [7] minimisation as a preprocessing step to refinement checking.
7 Conclusions
Our study of the antichain-based algorithms for deciding stable failures refinement and failures-divergences refinement presented in [21] revealed that the failures-divergences refinement algorithm is incorrect; both algorithms perform suboptimally when implemented using a depth-first search strategy and poorly when implemented using a breadth-first search strategy. Moreover, both violate the claimed antichain property. We have proposed alternative algorithms for which we showed correctness and which utilise proper antichains. Our experiments indicate significant performance improvements for deciding stable failures refinement and a performance of deciding failures-divergences refinement that is comparable to deciding stable failures refinement.
Notes
- 1.
- 2.
References
Abdulla, P.A., Chen, Y.-F., Holík, L., Mayr, R., Vojnar, T.: When simulation meets antichains. In: Esparza, J., Majumdar, R. (eds.) TACAS 2010. LNCS, vol. 6015, pp. 158–174. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-12002-2_14
Bergstra, J.A., Klop, J.W., Olderog, E.: Failures without chaos: a new process semantics for fair abstraction. In: Wirsing, M. (ed.) IFIP TC 2/WG 2.2 1986, pp. 77–104, North-Holland (1987)
van Beusekom, R., et al.: Formalising the Dezyne modelling language in mCRL2. In: Petrucci, L., Seceleanu, C., Cavalcanti, A. (eds.) FMICS/AVoCS -2017. LNCS, vol. 10471, pp. 217–233. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-67113-0_14
Brookes, S.D., Roscoe, A.W.: An improved failures model for communicating processes. In: Brookes, S.D., Roscoe, A.W., Winskel, G. (eds.) CONCURRENCY 1984. LNCS, vol. 197, pp. 281–305. Springer, Heidelberg (1985). https://doi.org/10.1007/3-540-15670-4_14
Bunte, O., et al.: The mCRL2 toolset for analysing concurrent systems. In: Vojnar, T., Zhang, L. (eds.) TACAS 2019. LNCS, vol. 11428, pp. 21–39. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17465-1_2
Gibson-Robinson, T., Armstrong, P., Boulgakov, A., Roscoe, A.W.: FDR3—a modern refinement checker for CSP. In: Ábrahám, E., Havelund, K. (eds.) TACAS 2014. LNCS, vol. 8413, pp. 187–201. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54862-8_13
van Glabbeek, R.J., Luttik, B., Trcka, N.: Branching bisimilarity with explicit divergence. Fundam. Inform. 93(4), 371–392 (2009). https://doi.org/10.3233/FI-2009-109
van Glabbeek, R.J.: Personal Communication, 7 January 2019
Glabbeek, R.: A branching time model of CSP. In: Gibson-Robinson, T., Hopcroft, P., Lazić, R. (eds.) Concurrency, Security, and Puzzles. LNCS, vol. 10160, pp. 272–293. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-51046-0_14
Gomes, A.O., Butterfield, A.: Modelling the haemodialysis machine with Circus. In: Butler, M., Schewe, K.-D., Mashkoor, A., Biro, M. (eds.) ABZ 2016. LNCS, vol. 9675, pp. 409–424. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-33600-8_34
Herlihy, M., Shavit, N.: The Art of Multiprocessor Programming. Morgan Kaufmann (2008)
Hoare, C.: Communicating Sequential Processes. Prentice-Hall, Upper Saddle River (1985)
Kanellakis, P.C., Smolka, S.A.: CCS expressions, finite state processes, and three problems of equivalence. Inf. Comput. 86(1), 43–68 (1990). https://doi.org/10.1016/0890-5401(90)90025-D
Laveaux, M., Groote, J.F., Willemse, T.A.C.: Correct and efficient antichain algorithms for refinement checking. CoRR abs/1902.09880 (2019)
Laveaux, M.: Downloadable sources and benchmarks for the experimental validation (2019). https://doi.org/10.5281/zenodo.2573095
Paval, R.: Modeling and verifying concurrent data structures. Master’s thesis, Eindhoven University of Technology (2018). https://research.tue.nl/files/93882157/Thesis_Roxana_Paval.pdf
Roscoe, A.W.: Model-checking CSP. In: Roscoe, A.W. (ed.) A Classical Mind: Essays in Honour of C.A.R. Hoare, Chap. 21, pp. 353–378. Prentice Hall International (UK) Ltd. (1994)
Roscoe, A.W.: Understanding Concurrent Systems. Texts in Computer Science. Springer, London (2010). https://doi.org/10.1007/978-1-84882-258-0
Shann, C., Huang, T., Chen, C.: A practical nonblocking queue algorithm using compare-and-swap. In: ICPADS 2000, pp. 470–475. IEEE Computer Society (2000). https://doi.org/10.1109/ICPADS.2000.857731
Treiber, R.K.: Systems programming: coping with parallelism. International Business Machines Incorporated. Thomas J. Watson Research (1986)
Wang, T., et al.: More anti-chain based refinement checking. In: Aoki, T., Taguchi, K. (eds.) ICFEM 2012. LNCS, vol. 7635, pp. 364–380. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34281-3_26
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 IFIP International Federation for Information Processing
About this paper
Cite this paper
Laveaux, M., Groote, J.F., Willemse, T.A.C. (2019). Correct and Efficient Antichain Algorithms for Refinement Checking. In: Pérez, J., Yoshida, N. (eds) Formal Techniques for Distributed Objects, Components, and Systems. FORTE 2019. Lecture Notes in Computer Science(), vol 11535. Springer, Cham. https://doi.org/10.1007/978-3-030-21759-4_11
Download citation
DOI: https://doi.org/10.1007/978-3-030-21759-4_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-21758-7
Online ISBN: 978-3-030-21759-4
eBook Packages: Computer ScienceComputer Science (R0)






 if there is some
if there is some  ,
, ,
,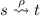 and
and 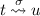 then
then 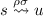 .
.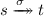 for some t. We denote the set of all traces starting in s by
for some t. We denote the set of all traces starting in s by  for some t. The set of all weak traces starting in s is denoted by
for some t. The set of all weak traces starting in s is denoted by  ; we define
; we define  and
and 
 , suggesting that refusals are also defined for unstable states. As we discuss in Sect.
, suggesting that refusals are also defined for unstable states. As we discuss in Sect. 