Abstract
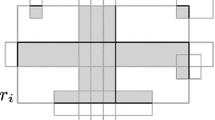
In this paper, we develop a simple technique for constructing a Binary Space Partition (BSP) for a set of orthogonal rectangles in ℝ3. Our algorithm has the novel feature that it tunes its performance to the geometric properties of the rectangles, e.g., their aspect ratios.
We have implemented our algorithm and tested its performance on real data sets. We have also systematically compared the performance of our algorithm with that of other techniques presented in the literature. Our studies show that our algorithm constructs BSPs of near-linear size and small height in practice, has fast running times, and answers queries efficiently. It is a method of choice for constructing BSPs for orthogonal rectangles.
A preliminary version of this paper appeared as a communication in the Proceedings of the 13th Annual ACM Symposium on Computational Geometry, 1997, pages 382–384.
This author is affiliated with Brown University. Support was provided in part by National Science Foundation research grant CCR-9522047 and by Army Research Office MURI grant DAAH04-96-1-0013.
Support was provided in part by National Science Foundation research grant CCR-93-01259, by Army Research Office MURI grant DAAH04-96-1-0013, by a Sloan fellowship, by a National Science Foundation NYI award and matching funds from Xerox Corp, and by a grant from the U.S.-Israeli Binational Science Foundation.
Support was provided in part by National Science Foundation research grant CCR-9522047, by Army Research Office grant DAAH04-93-G-0076, and by Army Research Office MURI grant DAAH04-96-1-0013.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
P. K. Agarwal, E. F. Grove, T. M. Murali, and J. S. Vitter, Binary space partitions for fat rectangles, Proc. 37th Annu. IEEE Sympos. Found. Comput. Sci., October 1996, pp. 482–491.
P. K. Agarwal and S. Suri, Surface approximation and geometric partitions, Proc. 5th ACM-SIAM Sympos. Discrete Algorithms, 1994, pp. 24–33.
J. M. Airey, Increasing Update Rates in the Building Walkthrough System with Automatic Model-space Subdivision and Potentially Visible Set Calculations, Ph.D. Thesis, Dept. of Computer Science, University of North Carolina, Chapel Hill, 1990.
A. T. Campbell, Modeling Global Diffiuse Illumination for Image Synthesis, Ph.D. Thesis, Dept. of Computer Sciences, University of Texas, Austin, 1991.
T. Cassen, K. R. Subramanian, and Z. Michalewicz, Near-optimal construction of partitioning trees by evolutionary techniques, Proc. Graphics Interface’ 95, 1995, pp. 263–271.
N. Chin and S. Feiner, Near real-time shadow generation using BSP trees, Proc. SIGGRAPH 89, Comput. Graph., Vol. 23, ACM SIGGRAPH, 1989, pp. 99–106.
N. Chin and S. Feiner, Fast object-precision shadow generation for areal light sources using BSP trees, Proc. 1992 Sympos. Interactive 3D Graphics, 1992, pp. 21–30.
M. de Berg, Linear size binary space partitions for fat objects, Proc. 3rd Annu. European Sympos. Algorithms, Lecture Notes Comput. Sci., Vol. 979, Springer-Verlag, 1995, pp. 252–263.
J. D. Foley, A. van Dam, S. K. Feiner, and J. F. Hughes, Computer Graphics: Principles and Practice, Addison-Wesley, Reading, MA, 1990.
H. Fuchs, Z. M. Kedem, and B. Naylor, On visible surface generation by a priori tree structures, Proc. SIGGRAPH 80, Comput. Graph., Vol. 14, ACMSIGGRAPH, 1980, pp. 124–133.
C. Mata and J. S. B. Mitchell, Approximation algorithms for geometric tour and network design problems, Proc. 11th Annu. ACM Sympos. Comput. Geom., 1995, pp. 360–369.
T. M. Murali and T. A. Funkhouser, Consistent solid and boundary representations from arbitrary polygonal data, Proc. 1997 Sympos. Interactive 3D Graphics, 1997, pp. 155–162.
M. J. Muus, Understanding the preparation and analysis of solid models, in: Techniques for Computer Graphics (D. F. Rogers and R. A. Earnshaw, eds.), Springer-Verlag, 1987.
B. Naylor, Constructing good partitioning trees, Proc. Graphics Interface’ 93, 1993, pp. 181–191.
B. Naylor and W. Thibault, Application of BSP trees to ray-tracing and CSG evaluation, Technical Report GIT-ICS 86/03, Georgia Institute of Tech., School of Information and Computer Science, February 1986.
B. F. Naylor, J. Amanatides, and W. C. Thibault, Merging BSP trees yields polyhedral set operations, Proc. SIGGRAPH 90, Comput. Graph., Vol. 24, ACM SIGGRAPH, 1990, pp. 115–124.
M. S. Paterson and F. F. Yao, Efficient binary space partitions for hidden-surface removal and solid modeling, Discrete Comput. Geom., 5 (1990), 485–503.
M. S. Paterson and F. F. Yao, Optimal binary space partitions for orthogonal objects, J. Algorithms, 13 (1992), 99–113.
R. A. Schumacker, R. Brand, M. Gilliland, and W. Sharp, Study for applying computer-generated images to visual simulation, Tech. Rep. AFHRL-TR-69-14, U.S. Air Force Human Resources Laboratory, 1969.
P. J. Tanenbaum. Applications of computational geometry in army research and development. Invited talk, Second CGC Workshop on Computational Geometry, 1997.
S. J. Teller, Visibility Computations in Densely Occluded Polyhedral Environments, Ph.D. Thesis, Dept. of Computer Science, University of California, Berkeley, 1992.
W. C. Thibault and B. F. Naylor, Set operations on polyhedra using binary space partitioning trees, Proc. SIGGRAPH 87, Comput. Graph., Vol. 21, ACM SIGGRAPH, 1987, pp. 153–162.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1998 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Murali, T.M., Agarwal, P.K., Vitter, J.S. (1998). Constructing Binary Space Partitions for Orthogonal Rectangles in Practice. In: Bilardi, G., Italiano, G.F., Pietracaprina, A., Pucci, G. (eds) Algorithms — ESA’ 98. ESA 1998. Lecture Notes in Computer Science, vol 1461. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-68530-8_18
Download citation
DOI: https://doi.org/10.1007/3-540-68530-8_18
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-64848-2
Online ISBN: 978-3-540-68530-2
eBook Packages: Springer Book Archive