Abstract
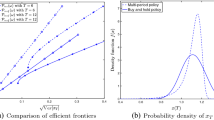
In real investment situations, one desires to only minimize downside risk or portfolio loss without affecting the upside potentials. This can be accomplished by mean semi-variance optimization but not by mean variance. In the Black-Scholes setting, this paper proposes for the very practical yet intractable dynamic mean semi-variance portfolio optimization problem, an almost analytical solution. It proceeds by reducing the multi-dimensional portfolio selection problem to a one-dimensional optimization problem, which is then expressed in terms of the normal density, leading to a very simple and efficient numerical algorithm. A numerical comparison of the efficient frontier for the mean variance and semi-variance portfolio optimization problem is presented.
This research was partially supported by the National Science and Engineering Research Council of Canada, and the Network Centre of Excellence, Mathematics of Information Technology and Complex Systems.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Duffie, D., Richardson, H.: Mean-variance hedging in continuous time. Annals of Applied Probability, 14 (1991) 1–15.
Fishburn, P.: Mean-risk analysis with risk associated with below-target returns. American Economic Review, 67 (1977) 116–125.
Hakansson, N.H.: Multi-period mean-variance analysis: Toward a general theory of portfolio choice. Journal of Finance, 26 (1971) 857–884.
Hull, J.: Options, Futures, and Other Derivatives, 5th edn. Prentice Hall, New Jersey, (2003).
Emmer, S., Klüuppelberg, C., Korn, R.: Optimal portfolios with bounded capital at risk. Mathematical Finance, 11 (2001) 365–384.
Lari-Lavassani, A., Li, X., Ware, A., Dmitrasinovic-Vidovic, G.: Dynamic portfolio selection under downside risks. Working paper, the Mathematical and Computational Finance Laboratory, University of Calgary, (2002).
Lari-Lavassani, A., Li, X.: Dynamic mean-variance portfolio selection with borrowing constraint. Preprint, the Mathematical and Computational Finance Laboratory, University of Calgary, (2002).
Lari-Lavassani, A., Li, X.: Continuous-time mean semi-variance portfolio selection. Preprint, the Mathematical and Computational Finance Laboratory, University of Calgary, (2003).
Li, D., Ng, W.L.: Optimal dynamic portfolio selection: Multi-period mean-variance formulation. Mathematical Finance, 10 (2000) 387–406.
Li, X.: Indefinite Stochastic LQ Control with Financial Applications. Dissertation, the Chinese University of Hong Kong, (2000).
Li, X., Zhou, X.Y., Lim, A.E.B.: Dynamic mean-variance portfolio selection with no-shorting constraints. SIAM Journal on Control and Optimization, 40 (2001) 1540–1555.
Markowitz, H.: Portfolio selection. Journal of Finance, 7 (1952) 77–91.
Steinbach, M.C.: Markowitz Revisited: Mean-Variance Models in Financial Portfolio Analysis. SIAM Review, 43 (2001) 31–85.
J. Yong and X.Y. Zhou. Stochastic Controls: Hamiltonian Systems and HJB Equations. Springer-Verlag, New York, 1999.
Zhou, X.Y., Li, D.: Continuous time mean-variance portfolio selection: A stochastic LQ framework. Applied Mathematics and Optimization, 42 (2000) 19–33.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2003 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Lari-Lavassani, A., Li, X. (2003). Dynamic Mean Semi-variance Portfolio Selection. In: Sloot, P.M.A., Abramson, D., Bogdanov, A.V., Dongarra, J.J., Zomaya, A.Y., Gorbachev, Y.E. (eds) Computational Science — ICCS 2003. ICCS 2003. Lecture Notes in Computer Science, vol 2657. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-44860-8_10
Download citation
DOI: https://doi.org/10.1007/3-540-44860-8_10
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-40194-0
Online ISBN: 978-3-540-44860-0
eBook Packages: Springer Book Archive