iBet uBet web content aggregator. Adding the entire web to your favor.

Den blå kurven er eksponentialfunksjonen, den grønne er den naturlige logaritmefunksjonen og den brune rette linjen er y=x. Eksponentialfunksjonen og den naturlige logaritmefunksjonen er den inverse funksjonen av hverandre.

tre kurver i koordinatsystem

Av Helge Holden.

Lisens: CC BY SA 3.0

Den inverse funksjonen til en matematisk funksjon \(y=f(x)\) er funksjonen der man finner \(x\) uttrykt ved hjelp av \(y\). Den skrives ofte \( x=f^{-1}(y)\). En invers funksjon kalles også en omvendt funksjon.

Faktaboks

Uttale: inv'ers
Også kjent som: omvendt funksjon

For funksjonen \(y=f(x)\) er \(x\) den uavhengige variabelen, og \(y\) er den avhengige variabelen. Dersom \(x\) er kjent, er altså \(y\) entydig bestemt ved funksjonen \(f\). Om man derimot starter med \(y\), og finner en entydig \(x\) slik at \(y=f(x)\), er dette den inverse funksjonen til \(f\). For at den inverse skal være en funksjon, må \(x\) være entydig bestemt ut fra \(f^{-1}(y)\)

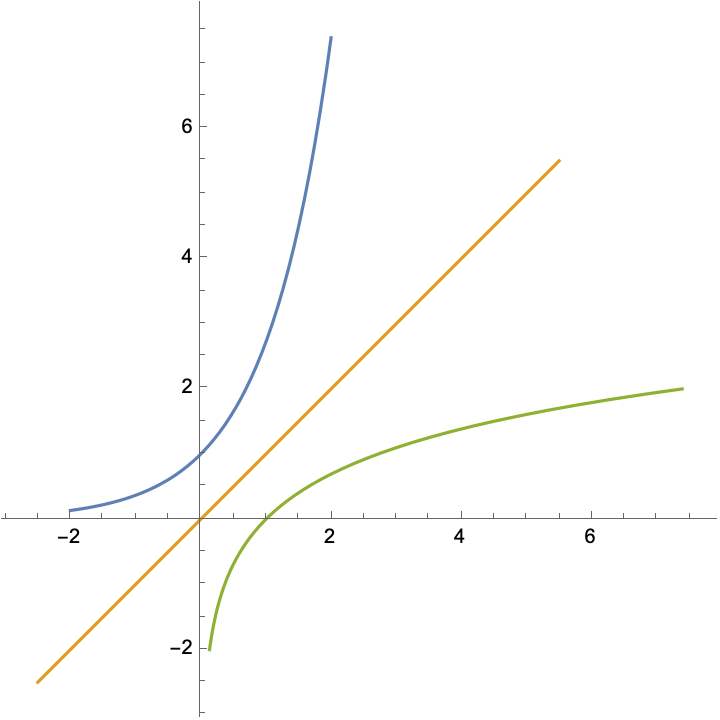
Grafisk fremstiller man den inverse funksjonen som refleksjonen av den opprinnelige funksjonen om den rette linjen \(y=x\).

En funksjon \(f\) er definert fra sin definisjonsmengde til sin verdimengde. Den inverse funksjonen er en funksjon fra verdimengden til definisjonsmengden. Den er bare veldefinert dersom \(f\) er en injeksjon.

Eksempler

For funksjonen \(y=f(x)=2x\), så er den inverse funksjonen \(x=f^{-1}(y)=y/2\).

For \(y=f(x)=e^x\), så er det \(x=f^{-1}(y)=\ln(y)\). Det vil si at eksponentialfunksjonen og den naturlige logaritmefunksjonen er inverse funksjoner.

Ikke alle funksjoner har en invers funksjon. Funksjonen \(y=y(x)=x^2\) har for eksempel ikke en invers funksjon. Ta for eksempel \(y=4\). Da vil både verdiene \(x=2\) og \(x=-2\) gjøre at \(y=x^2\), og dermed er ikke \(x\) entydig.

Les mer i Store norske leksikon

funksjon

Kommentarer

Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.

Du må være logget inn for å kommentere.

Fagansvarlig for Matematisk analyse

Helge Holden

Professor, NTNU – Norges teknisk-naturvitenskapelige universitet