gass-tilstandsligningen

For en ideal gass er tilstandsligningen

PV = nRT

Her er P trykket i gassen, målt i pascal eller atmosfære, V er volumet av gassen i liter, n er stoffmengden av gassen, R er gasskonstanten (i enheter som passer med valget av enhet for trykket) og T er temperaturen i kelvin i gassen.

Denne tilstandsligningen passer best for en temperatur som er høy i forhold til kokepunktet for stoffet gassen består av, og der trykket ikke er for høyt.

For en utledning av tilstandsligningen, se kinetisk gassteori.

Ligningen summerer opp forskjellige sammenhenger for gasser som ble funnet på 1600-tallet:

Johannes van der Waals foreslo en modifisert tilstandsligning i 1873:

(P + an²/V²)(V– nb) = nRT

Her er a og b to konstanter som må bestemmes eksperimentelt for hver gass ved tilpasning av ligningen til målinger.

Leddet a(n/V)² skyldes tiltrekkende krefter mellom molekylene i gassen, og n/V er tettheten av molekyler i gassen. Tiltrekningen er mellom to molekyler som er nær hverandre. Sannsynligheten for slike molekylpar er (n/V)². At det virker tiltrekkende krefter mellom molekylene, viser det faktum at alle gasser (unntatt hydrogengass) avkjøles når de utvides uten å utføre arbeid på omgivelsene. Det skjer ikke med en ideal gass.

Leddet b skyldes frastøtning mellom molekylene når de kommer nær hverandre. Da molekylene har en viss størrelse, er ikke hele gassvolumet tilgjengelig for molekylene.

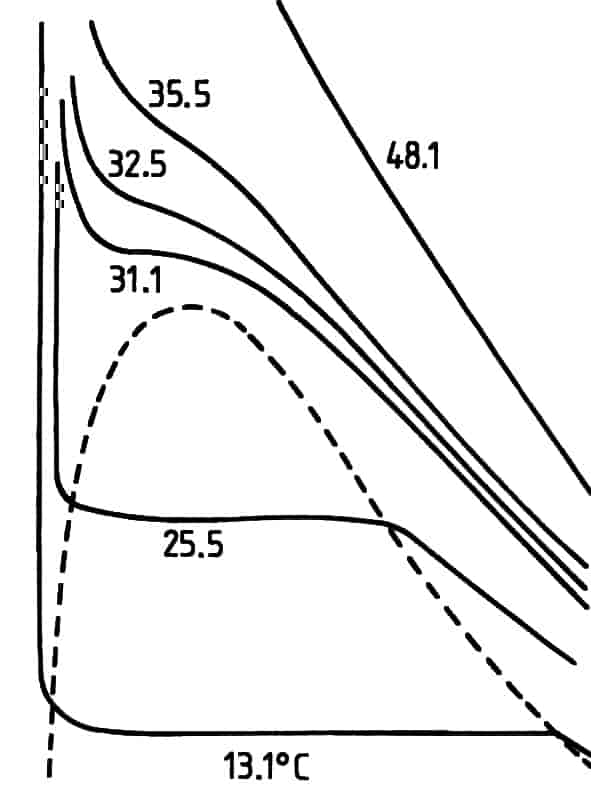
Van der Waals støttet seg særlig til eksperimentelle målinger gjort av av irske Thomas Andrews (1803–1885) på karbondioksidgass. De er vist i grafen i figuren. Her er P tegnet som funksjon av V ved forskjellige temperaturer. Den stiplete linjen omkranser området hvor karbondioksid både er i gass og væskeform. Over ca 30 ^oC er det ingen forskjell på væsken og gassen. Over denne temperaturen, som kalles den kritiske temperaturen, er det ikke mulig å kondensere en gass til en væske.

Van der Waals tilstandsligning er også en tilnærmet ligning. Det nye med den er at den ikke bare beskriver en gass, men også gassens overgang til en væske. Grafen i figuren er beregnet av van der Waals fra hans tilstandsligning. Den viser de samme trekkene som målingene til Andrews bortsett fra i tofaseområdet mellom punktene H og B.

I 1880 viste van der Waals at konstantene a og b kunne fjernes ved å innføre trykket, volumet og temperaturen ved den kritiske tilstand i sin tilstandsligning. Dette gjorde det mulig for hans venn og kollega Heike Kamerlingh Onnes å anslå det kritiske punktet for heliumgass slik at han i 1908 greide å fremstille helium i væskeform. For dette fikk Kamerlingh Onnes Nobelprisen i fysikk i 1913.

Cato Maximilian Guldberg hadde som mål allerede i 1868 å finne en tilstandsligning som ikke bare omfattet gasser og væsker, men også faste stoffer. Den lykkes han ikke i, men det er heller ingen andre som har greid det. Guldbergs regel fra 1890 sier at et stoffs kokepunkt er cirka ⅔ av den kritiske temperaturen i kelvin.

• gass
• kinetisk gassteori