Mediatoare

Construcția cercului circumscris unui triunghi (cu roșu) și a centrului cercului circumscris (punctul roșu)

În geometria plană, mediatoarea este perpendiculara dusă prin mijlocul unui segment. Mediatoarea poate fi definită și ca fiind locul geometric al punctelor egal depărtate de extremitățile segmentului.

Proprietăți

1. Cele trei mediatoare ale laturilor unui triunghi sunt concurente într-un punct care este centrul cercului circumscris triunghiului.

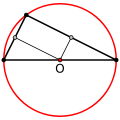
Demonstrație. Fie O – punctul de intersecție al mediatoarelor segmentelor AB și BC. Din definiția mediatoarei, rezultă că $|OA|=|OB|=|OC|$ ceea ce înseamnă că O aparține mediatoarei segmentului AC.

2. Proprietate: Un punct aparține mediatoarei unui segment dacă și numai dacă are distanțe egale față de extremitățile segmentului.

• 
  Centrul cercului circumscris al unui triunghi ascuțitunghic se află în interiorul triunghiului.
• 
  Centrul cercului circumscris al unui triunghi dreptunghic coincide cu mijlocul ipotenuzei.
• 
  Centrul cercului circumscris al unui triunghi obtuzunghic se află în exteriorul triunghiului.

3. Diametrul cercului circumscris este dat de formula:

${\begin{aligned}{\text{diametru}}&{}={\frac {2abc}{\sqrt {(a+b+c)(a-b+c)(b-c+a)(c-a+b)}}}\\&{}={\frac {2abc}{\sqrt {p(p-2*a)(p-2*b)(p-2*c)}}}\end{aligned}}$

unde a, b și c sunt lungimile laturilor unui triunghi oarecare, iar p este perimetrul acestuia.

Vezi și

• Bisectoare
• Mediană
• Înălțime (geometrie)