Cantelare
Aspect
| Deși acest articol conține o listă de referințe bibliografice, sursele sale rămân neclare deoarece îi lipsesc notele de subsol. Puteți ajuta introducând citări mai precise ale surselor. Întrucât este un articol tradus, a se vedea pagina de discuție, iar articolul de origine nu are nici el note de subsol, puteți ajuta și supraveghind acel articol, iar când acolo apar note de subsol, copiați-le și aici. |
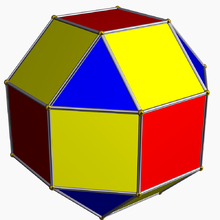
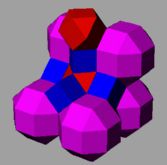
Pentru poliedre și pavări cantelarea corespunde deplasării fețelor formei regulate mai departe de centru, și completarea cu fețe noi a golurilor care apar în dreptul laturilor și vârfurilor inițiale. Operația mai este numită de către Alicia Boole Stott și expandare.
Notații
[modificare | modificare sursă]Un politop cantelat este reprezentat de un simbol Schläfli extins t0,2{p,q,...} sau r sau rr{p,q,...}.
Pentru poliedre, cantelarea oferă o metodă directă de transformare a unui poliedru regulat în dualul său.
Exemplu: secvența de cantelare de la cub la octaedru.

| ||||
| (poliedru regulat) cub |
cantelat 1/4 (cub teșit) |
cantelat uniform rombicuboctaedru |
cantelat 3/4 (octaedru teșit) |
(dual regulat) octaedru |
Alt exemplu: un cuboctaedru este un tetraedru cantelat.
Pentru politopurile din dimensiuni superioare, cantelarea oferă o metodă directă de transformare de la un politop regulat la forma sa birectificată.
Exemple de poliedre și pavări cantelate
[modificare | modificare sursă]| Tip | Poliedre | Pavări | |||
|---|---|---|---|---|---|
| Coxeter | rTT | rCO | rID | rQQ | rHΔ |
| Notația Conway |
eT | eC = eO | eI = eD | eQ | eH = eΔ |
| Poliedre de cantelat |
Tetraedru | Cub sau octaedru |
Icosaedru or dodecaedru |
Pavare pătrată | Pavare hexagonală Pavare triunghiulară |
| Imagine | 
|

|

|

|

|
| Animație | 
|

|

|
||
| Coxeter | rrt{2,3} | rrs{2,6} | rrCO | rrID |
|---|---|---|---|---|
| Notația Conway |
eP3 | eA4 | eaO = eaC | eaI = eaD |
| Poliedre de cantelat |
Prismă triunghiulară sau Bipiramidă |
Antiprismă pătrată sau Trapezoedru tetragonal |
Cuboctaedru sau dodecaedru rombic |
Icosidodecaedru sau triacontaedru rombic |
| Imagine | 
|

|

|

|
| Animație | 
|

|
Bibliografie
[modificare | modificare sursă]- en Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN: 0-486-61480-8 (pp.145-154 Chapter 8: Truncation, p 210 Expansion)
- en Norman Johnson, Uniform Polytopes, Manuscript (1991)
- en Norman Johnson, The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
Legături externe
[modificare | modificare sursă]- en Eric W. Weisstein, Expansion la MathWorld.
| Operatori poliedrici | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Sămânță | Trunchiere | Rectificare | Bitrunchiere | Dual | Expandare | Omnitrunchiere | Alternări | ||

|

|

|

|

| |||||
| t0{p,q} {p,q} |
t01{p,q} t{p,q} |
t1{p,q} r{p,q} |
t12{p,q} 2t{p,q} |
t2{p,q} 2r{p,q} |
t02{p,q} rr{p,q} |
t012{p,q} tr{p,q} |
ht0{p,q} h{q,p} |
ht12{p,q} s{q,p} |
ht012{p,q} sr{p,q} |



