iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://pubmed.ncbi.nlm.nih.gov/35733267
Quantifying the environmental limits to fire spread in grassy ecosystems - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 Jun 28;119(26):e2110364119.
doi: 10.1073/pnas.2110364119. Epub 2022 Jun 22.

Quantifying the environmental limits to fire spread in grassy ecosystems

Anabelle W Cardoso  1   2 , Sally Archibald  2 , William J Bond  3 , Corli Coetsee  4   5 , Matthew Forrest  6 , Navashni Govender  5   7 , David Lehmann  8 , Loïc Makaga  8 , Nokukhanya Mpanza  4 , Josué Edzang Ndong  8 , Aurélie Flore Koumba Pambo  8 , Tercia Strydom  4   9 , David Tilman  10 , Peter D Wragg  11 , A Carla Staver  1
Affiliations

Quantifying the environmental limits to fire spread in grassy ecosystems

Anabelle W Cardoso et al. Proc Natl Acad Sci U S A. .

Abstract

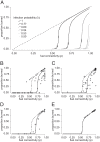
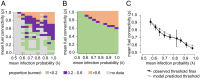
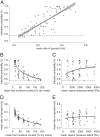
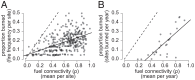
Modeling fire spread as an infection process is intuitive: An ignition lights a patch of fuel, which infects its neighbor, and so on. Infection models produce nonlinear thresholds, whereby fire spreads only when fuel connectivity and infection probability are sufficiently high. These thresholds are fundamental both to managing fire and to theoretical models of fire spread, whereas applied fire models more often apply quasi-empirical approaches. Here, we resolve this tension by quantifying thresholds in fire spread locally, using field data from individual fires (n = 1,131) in grassy ecosystems across a precipitation gradient (496 to 1,442 mm mean annual precipitation) and evaluating how these scaled regionally (across 533 sites) and across time (1989 to 2012 and 2016 to 2018) using data from Kruger National Park in South Africa. An infection model captured observed patterns in individual fire spread better than competing models. The proportion of the landscape that burned was well described by measurements of grass biomass, fuel moisture, and vapor pressure deficit. Regionally, averaging across variability resulted in quasi-linear patterns. Altogether, results suggest that models aiming to capture fire responses to global change should incorporate nonlinear fire spread thresholds but that linear approximations may sufficiently capture medium-term trends under a stationary climate.

Keywords: fire model; fire thresholds; fuel moisture; infection model; percolation.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interest.

Figures

Fig. 1.
Fig. 1.
Response of burned area (proportion burned) to fuel connectivity (ρ) in simulation (A; also depending on infection probability λ) and in empirical observations from Kruger National Park, South Africa (B; 496 to 737 mm MAP), Hluhluwe-iMfolozi, South Africa (C; 600 to 1,000 mm MAP), the Cedar Creek Ecosystem Science Reserve, East Bethel, MN (D; 775 mm MAP), and Lopé National Park, Gabon (E; 1,442 mm MAP). In B–E, dotted lines show the infection model simulation for λ = 1 and solid lines show the simulation with λ that minimized distance index (Materials and Methods) for the observed data (Kruger λ = 0.71, n = 61; HiP λ = 0.74, n = 30; Cedar Creek λ = 0.77, n = 66; Lopé λ = 1, n = 31). In all cases (B–E) the infection model was a better fit (lower distance index) to the data than linear, quadratic, two linear, exponential, logistic, van Bertalanffy, and Gompertz models.
Fig. 2.
Fig. 2.
Variation in burned area (proportion burned) with fuel connectivity (ρ) and infection probability (λ) in observed fires in Kruger (A) and according to model simulations (B). The response of the fire spread threshold to fuel connectivity (ρ) and infection probability (λ) is also explored in theory and in observed fires in Kruger through examination of “threshold fires” (those with burned area between 0.2 and 0.6, shown in purple in A and B). (C) The mean (± SE, minimum, maximum) values of fuel connectivity (ρ) and infection probability (λ) for all “threshold fires” was 0.72 (±0.04, 0.56, 0.91) and 0.77 (±0.05, 0.58, 0.98), respectively.
Fig. 3.
Fig. 3.
Response of the estimated fire infection probability (λ) to its mean rate of spread (ROS) (A) and response of fire infection probability (λ) and fire rate of spread to fuel moisture (FM) (B and D) and vapor pressure deficit (VPD) (C and E). Fitted curves show linear model results with SEs of fits shown in gray. A: λ=0.92*ROS+0.55;  adjusted R2 = 0.53, P < 0.0001. B and C: λ=−0.15*ln(FM)+0.07*ln (VPD)+0.88; adjusted R2 = 0.65, P < 0.0001. D and E: ROS=−0.13*ln(FM)+0.02*ln(VPD)+0.59; adjusted R2 = 0.77, P < 0.0001. In B and D, the curve shows predictions when VPD is held at a constant value of 2,004 Pa, and in C and E when FM is held at a constant value of 43% (the median value observed in the dataset). In A–C, dashed lines show the minimum infection probability (λ = 0.58) in observed “threshold fires” (those with burned area between 0.2 and 0.6) below which fire cannot successfully spread.
Fig. 4.
Fig. 4.
Response of site fire frequency (proportion burned) to average site fuel connectivity (ρ) across Kruger (A) and of park-wide burned area (proportion burned) to parkwide average fuel connectivity (ρ) across years (B). Fire frequency increases with average fuel connectivity of a site (slope = 0.24, intercept = 0.05, adjusted R2 = 0.25, P < 0.0001) and annual park burned area increases with the fuel connectivity of the park in any given year (slope = 0.62, intercept = 0.20, adjusted R2 = 0.59, P < 0.0001). All dotted lines show the relationship y = x, which represents the maximum possible burned area given the fuel connectivity of a landscape.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Bowman D. M. J. S., et al. , Fire in the earth system. Science 324, 481–484 (2009). - PubMed
    1. Andela N., et al. , A human-driven decline in global burned area. Science 356, 1356–1362 (2017). - PMC - PubMed
    1. Van Der Werf G. R., et al. , Global fire emissions and the contribution of deforestation, savanna, forest, agricultural, and peat fires (1997-2009). Atmos. Chem. Phys. 10, 11707–11735 (2010).
    1. Cuddington K., et al. , Process-based models are required to manage ecological systems in a changing world. Ecosphere 4, 1–12 (2013).
    1. Bradstock R. A., A biogeographic model of fire regimes in Australia: Current and future implications. Glob. Ecol. Biogeogr. 19, 145–158 (2010).

Publication types