iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://pubmed.ncbi.nlm.nih.gov/30478209
Statistical physics models for aftershocks and induced seismicity - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2018 Nov 26;377(2136):20170397.
doi: 10.1098/rsta.2017.0397.

Statistical physics models for aftershocks and induced seismicity

Molly Luginbuhl  1 , John B Rundle  2   3   4 , Donald L Turcotte  3
Affiliations
Review

Statistical physics models for aftershocks and induced seismicity

Molly Luginbuhl et al. Philos Trans A Math Phys Eng Sci. .

Abstract

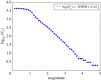
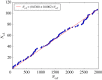
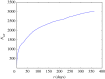
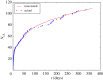
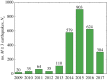
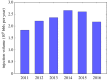
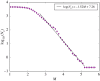
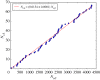
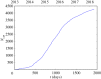
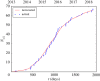
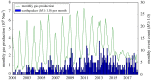
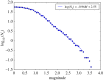
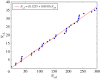
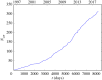
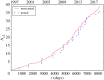
A standard approach to quantifying the seismic hazard is the relative intensity (RI) method. It is assumed that the rate of seismicity is constant in time and the rate of occurrence of small earthquakes is extrapolated to large earthquakes using Gutenberg-Richter scaling. We introduce nowcasting to extend RI forecasting to time-dependent seismicity, for example, during an aftershock sequence. Nowcasting uses 'natural time'; in seismicity natural time is the event count of small earthquakes. The event count for small earthquakes is extrapolated to larger earthquakes using Gutenberg-Richter scaling. We first review the concepts of natural time and nowcasting and then illustrate seismic nowcasting with three examples. We first consider the aftershock sequence of the 2004 Parkfield earthquake on the San Andreas fault in California. Some earthquakes have higher rates of aftershock activity than other earthquakes of the same magnitude. Our approach allows the determination of the rate in real time during the aftershock sequence. We also consider two examples of induced earthquakes. Large injections of waste water from petroleum extraction have generated high rates of induced seismicity in Oklahoma. The extraction of natural gas from the Groningen gas field in The Netherlands has also generated very damaging earthquakes. In order to reduce the seismic activity, rates of injection and withdrawal have been reduced in these two cases. We show how nowcasting can be used to assess the success of these efforts.This article is part of the theme issue 'Statistical physics of fracture and earthquakes'.

Keywords: aftershocks; induced seismicity; natural time; nowcasting.

PubMed Disclaimer

Conflict of interest statement

There are no competing interests for this manuscript.

Figures

Figure 1.
Figure 1.
The cumulative frequency-magnitude distribution of earthquakes in the study region for 365 days starting 0.1 days after the Parkfield mainshock. The cumulative number of earthquakes per year Nc with magnitudes greater than M are given as a function of M. The best fit of the GR scaling from equation (1.1) is also given, b = 0.96 and a = 4.44. (Online version in colour.)
Figure 2.
Figure 2.
Dependence of the cumulative number of large aftershocks with magnitudes greater than Mλ≥2.5, Ncλ, on the cumulative number of small aftershocks with magnitudes greater than Mσ≥1.0, Ncσ (natural time). The data are for 365 days starting 0.1 days after the mainshock. The least-squares linear fit passing through the origin is shown. (Online version in colour.)
Figure 3.
Figure 3.
Dependence of the cumulative number of small aftershocks, Ncσ, with magnitudes Mσ≥1.0 (natural time) on clock time, t in days beginning 0.1 days after the mainshock. (Online version in colour.)
Figure 4.
Figure 4.
Dependence of the cumulative number of large aftershocks, Ncλ, with magnitudes greater than Mλ≥2.5 on clock time in days beginning 0.1 days after the mainshock. Also included is the nowcast of these earthquakes obtained by multiplying the data given in figure 3 by the slope of the data in figure 2, 0.0360. (Online version in colour.)
Figure 5.
Figure 5.
Annual numbers of earthquakes in Oklahoma with magnitudes M≥3 for the period 2009–2017. (Online version in colour.)
Figure 6.
Figure 6.
Annual volumes of saline water injections in Oklahoma for the period 2011–2016. (Online version in colour.)
Figure 7.
Figure 7.
Cumulative frequency-magnitude distribution of earthquakes in Oklahoma for the period 1 January 2013–13 April 2018. The cumulative number of earthquakes per year Nc with magnitudes greater than M are given as a function of M. The straight line correlation is the least-squares fit with the GR scaling from equation (1.1). (Online version in colour.)
Figure 8.
Figure 8.
Dependence of the cumulative number of large earthquakes in Oklahoma with magnitudes Mλ≥4.0, Ncλ, on the cumulative number of small earthquakes with magnitudes Mσ≥2.75, Ncσ (natural time). The data are from the Oklahoma Geological Survey catalogue for the period 1 January 2013–13 April 2018. The least-squares linear fit to the data passing through the origin is also shown. (Online version in colour.)
Figure 9.
Figure 9.
Dependence of the cumulative number of small earthquakes, Ncσ, in Oklahoma with magnitudes Mσ≥2.75 (natural time) on the clock time, t, in days since 1 January 2013. (Online version in colour.)
Figure 10.
Figure 10.
Dependence of the cumulative number of large earthquakes in Oklahoma with magnitudes Mλ≥4.0 on clock time, t, in days since 1 January 2013. Also included is the nowcast of these earthquakes obtained by multiplying the data given in figure 9 by the slope of the data given in figure 8, 0.0154. (Online version in colour.)
Figure 11.
Figure 11.
Monthly natural gas production and monthly numbers of earthquakes with M≥1 for the Groningen gas field are given for the period 1 January 2001–30 June 2018. (Online version in colour.)
Figure 12.
Figure 12.
Cumulative frequency-magnitude distribution of earthquakes in the Groningen region for the period 1 January 1996–30 July 2018. The cumulative number of earthquakes per year, Nc, with magnitudes greater than M are given as a function of M. The straight line correlation is the least-squares fit with the GR scaling from equation (1.1). (Online version in colour.)
Figure 13.
Figure 13.
Dependence of the cumulative number of large earthquakes in the Groningen gas field with magnitudes Mλ≥2.5, Ncλ, on the cumulative number of small earthquakes, Ncσ (natural time), with magnitudes Mσ≥1.5 for the period 1 January 1996–30 July 2018. The data are from the KNMI catalogue. The least-squares linear fit to the data passing through the origin is also shown. (Online version in colour.)
Figure 14.
Figure 14.
Dependence of the cumulative number of small earthquakes, Ncσ, in the Groningen region with magnitudes Mσ≥1.5 (natural time) on clock time, t, in days since 1 January 1996. (Online version in colour.)
Figure 15.
Figure 15.
Dependence of the cumulative number of large earthquakes in the Groningen region with magnitudes Mλ≥2.5, Ncλ, on clock time t in days since 1 January 1996. Also included is the nowcast of these earthquakes obtained by multiplying the data given in figure 13 by the slope of the data in figure 14, 0.1235. (Online version in colour.)
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Varotsos PA, Sarlis NV, Skordas ES. 2002. Long-range correlations in the electric signals that precede rupture. Phys. Rev. E 66, 011902 (10.1103/PhysRevE.66.011902) - DOI - PubMed
    1. Varotsos PA, Sarlis NV, Tanaka HK, Skordas ES. 2005. Some properties of the entropy in the natural time. Phys. Rev. E 71, 032102 (10.1103/physreve.71.032102) - DOI - PubMed
    1. Sarlis N, Skordas E, Varotsos P. 2010. Nonextensivity and natural time: the case of seismicity. Phys. Rev. E 82, 021110 (10.1103/PhysRevE.82.021110) - DOI - PubMed
    1. Varotsos P, Sarlis N, Skordas E. 2011. Scale-specific order parameter fluctuations of seismicity in natural time before mainshocks. EPL (Europhysics Letters) 96, 59002 (10.1209/0295-5075/96/59002) - DOI
    1. Varotsos P, Sarlis NV, Skordas ES, Uyeda S, Kamogawa M. 2011. Natural time analysis of critical phenomena. Proc. Natl Acad. Sci. USA 108, 11 361–11 364. (10.1073/pnas.1108138108) - DOI - PMC - PubMed

LinkOut - more resources