iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://pubmed.ncbi.nlm.nih.gov/24904924
Diffeomorphometry and geodesic positioning systems for human anatomy - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2014 Mar;2(1):36.
doi: 10.1142/S2339547814500010.

Diffeomorphometry and geodesic positioning systems for human anatomy

Michael I Miller, Laurent Younes, Alain Trouvé

Diffeomorphometry and geodesic positioning systems for human anatomy

Michael I Miller et al. Technology (Singap World Sci). 2014 Mar.

Abstract

The Computational Anatomy project has largely been a study of large deformations within a Riemannian framework as an efficient point of view for generating metrics between anatomical configurations. This approach turns D'Arcy Thompson's comparative morphology of human biological shape and form into a metrizable space. Since the metric is constructed based on the geodesic length of the flows of diffeomorphisms connecting the forms, we call it diffeomorphometry. Just as importantly, since the flows describe algebraic group action on anatomical submanifolds and associated functional measurements, they become the basis for positioning information, which we term geodesic positioning. As well the geodesic connections provide Riemannian coordinates for locating forms in the anatomical orbit, which we call geodesic coordinates. These three components taken together - the metric, geodesic positioning of information, and geodesic coordinates - we term the geodesic positioning system. We illustrate via several examples in human and biological coordinate systems and machine learning of the statistical representation of shape and form.

PubMed Disclaimer

Figures

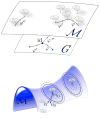
Figure 1
Figure 1
Top panel shows the orbit of forms M, and acting group G. Bottom panel shows radial representation of geodesic flattening of forms. Tangent space norm and geodesic distance agree for radial great circles emanating from the template m0 with distance formula image(m0,n) = ||v0||V.
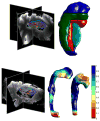
Figure 2
Figure 2
Showing mapping in high field 11.7T hippocampus depicting the partition into CA1 (blue), CA2 (green), CA3/Dentate (red) and Subiculum (cyan) of target structures exhibiting temporal lobe atrophy. Top shows four structures in section from the template corresponding to an age controlled normal showing reconstructions of CA1, CA2, CA3/ Dentate, subiculum. Bottom shows template mapped to the target an individual suffering from temporal lobe atrophy; right structures are CA1, CA3/Dentate colored with Jacobian determinant. Data collected is three-dimensional diffusion tensor imaging and was performed using a horizontal-bore 11.7 T NMR scanner (Bruker Biospin, Billerica, MA). DTI data were acquired with a 3D diffusion-weighted EPI sequence (TE = 27 ms, TR = 500 ms). The imaging field-of-view was 42 mm × 45 mm × 64 mm. Two b0 images and 30 diffusion directions were acquired within a scan time of 13.5 hours for DTI mapping.
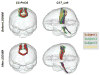
Figure 3
Figure 3
Geodesic positioning of the DT-MRI and alignment of fiber tracts. Three-dimensional diffusion tensor imaging of 20 subjects were performed on a 1.5T Siemens MR unit using single-shot echo-planar imaging sequences with sensitivity encoding (SENSE EPI) with parallel imaging factor of 2.0 (imaging matrix: 96 × 96, field-of-view: 240 mm × 240 mm, and slice thickness 2.5 mm). B0 images and DWIs of 30 diffusion directions were acquired and co-registered to remove eddy current and motion. The scanning time was 4 min per dataset. Tensor calculation was performed, followed by rigid alignment of all subjects. Fiber reconstructions were performed in each subject’s space using FACT tract tracing algorithm . CC-PoCG fiber: the starting and ending points of tract tracing were selected as the post-central gyri (PoCG) of the two hemispheres, and the fiber path was constraint to penetrate the corpus callosum (CC). CST_left fiber: the starting and ending points were the cerebral peduncle (CP) and the pre-central gyrus (PrCG); the fiber path was constrained by the posterior limb of internal capsule (PLIC) and the superior corona radiata (SCR). Top row shows the tracts in native brain (4 subjects were shown for demonstration); bottom row shows tracts after geodesic positioning via LDDMM solution of control problem 1.
Figure 4
Figure 4
Panel shows structures indexed by two highest variance dimensions from PCA on Riemannian exponential coordinates representing hippocampus structures from the BIOCARD study. Each structure is placed on the 2D plane with the template (red) at (0,0) in the center, left/right corresponding to the first dimension, and up/down corresponding to the second.
Figure 5
Figure 5
Panel shows results of machine learning (LDA) on the geodesic coordinates for sets of temporal lobe structures, amygdala-entorhinal cortex-hippocampus, with 50% witheld for training. Up to 50 points are placed for each group, with three examples from each group shown as surfaces. Red: normal elderly subjects, green: subjects diagnosed with Alzheimer’s disease at time of their last scan, blue: subjects diagnosed subsequent to their last scan and termed pre-clinical.
Figure 6
Figure 6
Top section: A high resolution computed tomography left ventricular template (1 mm isotropic) constructed from 25 subjects in AHA segmentation represented by one color per segment; black area within AHA anterior apical segment 13, showing statistical significance between two different populations of cardiac disease, ischemic (n = 13, 10 men, mean age 56) and non-ischemic cardiomyopathy (n = 12, 8 men, mean age 52) at end-systole. Each subject was studied either in a 32 (n = 8) or 64-detector (n = 17) multi-detector computed tomography scanner (Aquilion 32(64), Toshiba Medical Systems Corporation, Otawara, Japan). Plane resolution varied from 0.36 × 0.36 mm to 0.45 × 0.45 mm, thickness = 0.5 mm. Bottom section shows average Jacobian for ischemic (left) and non-ischemic (right) groups within segment 13 highlighting that on average non-ischemic group had significantly larger tissue (myocardial) volume relative to ischemic group at end-systole. This indicates smaller wall thickening during maximum contraction at the location of infarction in ischemic population.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Younes L. Shapes and diffeomorphisms. Shapes and Diffeomorphisms. 2010;171:1–434.
    1. Christensen GE, Rabbitt RD, Miller MI. Deformable templates using large deformation kinematics. IEEE Trans Image Process. 1996;5:1435–1447. - PubMed
    1. Trouve A. Action de groupe de dimension intinie et reconnaissance de formes. C R Acad Sci Paris Ser 1 Math. 1995;321:1031–1034.
    1. Dupuis P, Grenander U, Miller MI. Variational problems on flows of diffeomorphisms for image matching. Quart Appl Math. 1998;56:587–600.
    1. Avants BB, Schoenemann PT, Gee JC. Lagrangian frame diffeomorphic image registration: Morphometric comparison of human and chimpanzee cortex. Med Image Anal. 2006;10:397–412. - PubMed

LinkOut - more resources