iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://pubmed.ncbi.nlm.nih.gov/20885934/
A bayesian generative model for surface template estimation - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2010:2010:974957.
doi: 10.1155/2010/974957. Epub 2010 Sep 20.

A bayesian generative model for surface template estimation

Jun Ma  1 , Michael I Miller, Laurent Younes
Affiliations

A bayesian generative model for surface template estimation

Jun Ma et al. Int J Biomed Imaging. 2010.

Abstract

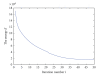
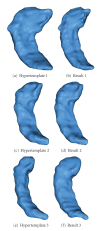
3D surfaces are important geometric models for many objects of interest in image analysis and Computational Anatomy. In this paper, we describe a Bayesian inference scheme for estimating a template surface from a set of observed surface data. In order to achieve this, we use the geodesic shooting approach to construct a statistical model for the generation and the observations of random surfaces. We develop a mode approximation EM algorithm to infer the maximum a posteriori estimation of initial momentum μ, which determines the template surface. Experimental results of caudate, thalamus, and hippocampus data are presented.

PubMed Disclaimer

Figures

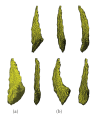
Figure 1
Figure 1
Random deformation of a template caudate surface (left). The six surfaces following the template are independent realization of the model described in (9).
Figure 2
Figure 2
Estimating the surface template from 9 caudate data. (a)–(i) observed surfaces. (j) is the hypertemplate. (k) is the result.
Figure 3
Figure 3
Estimating the surface template from 9 thalamus data. (a)–(i) observed surfaces. (j) is the hypertemplate. (k) is the result.
Figure 4
Figure 4
Estimating the surface template from 101 data. (a)–(h) are 8 examples out of 101 observed surfaces. (i) is the hypertemplate. (j) is the result.
Figure 5
Figure 5
Energy change with the iteration.
Figure 6
Figure 6
For the same observed population, we choose different surfaces as hypertemplate. The results only have minor differences.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Durrleman S, Pennec X, Trouvé A, Ayache N. A forward modelto build unbiased atlases from curves and surfaces. In: Proceedings of the International Workshop on the Mathematical Foundations of Computational Anatomy (MFCA ’08); September 2008; New York, NY, USA.
    1. Shen L, Farid H, McPeek MA. Modeling three-dimensional morphological structures using spherical harmonics. Evolution. 2008;63(4):1003–1016. - PMC - PubMed
    1. Guimond A, Meunier J, Thirion J-P. Average brain models: a convergence study. Computer Vision and Image Understanding. 2000;77(2):192–210.
    1. Mio W, Srivastava A, Joshi S. On shape of plane elastic curves. International Journal of Computer Vision. 2007;73(3):307–324.
    1. Fletcher PT, Joshi S, Lu C, Pizer SM. Principal geodesic analysis for the study of nonlinear statistics of shape. IEEE Transactions on Medical Imaging. 2004;23(8):995–1005. - PubMed