iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://pubmed.ncbi.nlm.nih.gov/19957039/
A model of the lower limb for analysis of human movement - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2010 Feb;38(2):269-79.
doi: 10.1007/s10439-009-9852-5. Epub 2009 Dec 3.

A model of the lower limb for analysis of human movement

Edith M Arnold  1 , Samuel R Ward, Richard L Lieber, Scott L Delp
Affiliations

A model of the lower limb for analysis of human movement

Edith M Arnold et al. Ann Biomed Eng. 2010 Feb.

Abstract

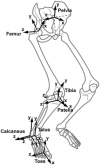
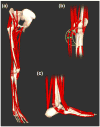
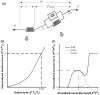
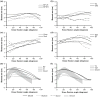
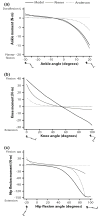
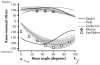
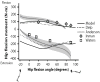
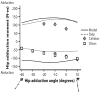
Computer models that estimate the force generation capacity of lower limb muscles have become widely used to simulate the effects of musculoskeletal surgeries and create dynamic simulations of movement. Previous lower limb models are based on severely limited data describing limb muscle architecture (i.e., muscle fiber lengths, pennation angles, and physiological cross-sectional areas). Here, we describe a new model of the lower limb based on data that quantifies the muscle architecture of 21 cadavers. The model includes geometric representations of the bones, kinematic descriptions of the joints, and Hill-type models of 44 muscle-tendon compartments. The model allows calculation of muscle-tendon lengths and moment arms over a wide range of body positions. The model also allows detailed examination of the force and moment generation capacities of muscles about the ankle, knee, and hip and is freely available at www.simtk.org .

PubMed Disclaimer

Figures

FIGURE 1
FIGURE 1
The coordinate systems of the bone segments. The systems are oriented so that when all joint angles are 0° the x-axes points anteriorly, the y-axes points superiorly, and the z-axes points to the right (laterally for the right leg). The joints in the model are defined as translations and rotations between these coordinate systems.
FIGURE 2
FIGURE 2
Three-dimensional model of the lower limb. (a) Bony geometry included models of the pelvis, femur, patella, tibia, fibula, talus, calcaneus, metatarsals, and phalanges. Muscle–tendon geometry used line segment paths constrained to origin and insertion points, wrapping surfaces (e.g., cylinder in b) and via points (e.g., highlighted points in c).
FIGURE 3
FIGURE 3
Hill-type model of muscle used to estimate tendon and muscle force. (a) The muscle–tendon length (lMT) derived from the muscle–tendon geometry was used to compute muscle fiber length (lM), tendon length (lT), pennation angle (α) muscle force (FM), and tendon force (FT). (b) Tendon was represented as a non-linear elastic element. We assumed that the stain in tendon ((lT−lST)/lST) was 0.033 when muscle generated maximum isometric force (FoM). Muscle was represented as a passive elastic element in parallel with an active contractile element (CE). Normalized active and passive force length curves were scaled by maximum isometric force (FoM) and optimal fiber length (loM) derived from experimental measurements for each muscle.
FIGURE 4
FIGURE 4
Moment arms of muscles crossing the knee in the model (solid), Buford et al. (dashed), Spoor and van Leeuwen (dot-dashed), and Grood et al. (shaded area). Muscle moment arms are shown for (a) biceps femoris long head (BFLH) and biceps femoris short head (BFSH), (b) gastrocnemius lateralis (GL) and gastrocnemius medialis (GM), (c) gracilis (Grac) and sartorius (Sart), (d) semimembranosus (SM) and semitendinosus (ST), (e) rectus femoris (RF), vastus intermedius (VI), and grouped quadriceps (Quad), and (f) vastus lateralis (VL), vastus medialis (VM), and grouped quadriceps (Quad).
FIGURE 5
FIGURE 5
Passive joint moments calculated by the model and measured experimentally. Passive joint moment was summed from all muscles crossing each joint and compared to experimental results reported by Riener et al. and Anderson et al. There are no experimental results for passive adduction/abduction moments. The joints of the model were positioned to match those used by Anderson et al. The ankle moment (a) was calculated when knee and hip flexion angles were 80° and 50°. The knee moment (b) was calculated when the hip flexion and ankle angles were 70° and 0°. The hip flexion moment (c) was calculated when the knee angle was 10°.
FIGURE 6
FIGURE 6
Maximum isometric ankle moments over a range of ankle angles. Dorsiflexion moments and angles are positive; plantarflexion moments and angles are negative. The moments estimated with the model were compared to a previous model described by Delp et al. and experimental data reported by Anderson et al., Marsh et al., and Sale et al. The gray region indicates one standard deviation of the data reported by Anderson et al.
FIGURE 7
FIGURE 7
Maximum isometric knee moments over a range of knee angles. Flexion moments and angles are positive; extension moments are negative. The moments estimated with the model were compared to a previous model described by Delp et al. and experimental data reported by Anderson et al., Murray et al., and Van Eijden et al. The gray region indicates one standard deviation of the data reported by Anderson et al.
FIGURE 8
FIGURE 8
Maximum isometric hip flexion moments over a range of hip flexion angles. Flexion moments and angles are positive; extension moments and angles are negative. The moments estimated with the model were compared to a previous model described by Delp et al. and experimental data reported by Anderson et al., Inman et al., and Waters et al. The gray region indicates one standard deviation of the data reported by Anderson et al.
FIGURE 9
FIGURE 9
Maximum isometric hip adductor moments over a range of hip adduction angles. Adduction moments and angles are positive; abduction moments and angles are negative. The moments estimated with the model were compared to a previous model described by Delp et al. and experimental data reported by Cahalan et al. and Olson et al.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Anderson DE, Madigan ML, Nussbaum MA. Maximum voluntary joint torque as a function of joint angle and angular velocity: model development and application to the lower limb. J Biomech. 2007;40:3105–3113. - PMC - PubMed
    1. Arnold AS, Asakawa DJ, Delp SL. Do the hamstrings and adductors contribute to excessive internal rotation of the hip in persons with cerebral palsy? Gait Posture. 2000;11:181–190. - PubMed
    1. Arnold AS, Blemker SS, Delp SL. Evaluation of a deformable musculoskeletal model for estimating muscle-tendon lengths during crouch gait. Ann Biomed Eng. 2001;29:263–274. - PubMed
    1. Arnold AS, Salinas S, Asakawa DJ, Delp SL. Accuracy of muscle moment arms estimated from MRI-based musculoskeletal models of the lower extremity. Comput Aided Surg. 2000;5:108–119. - PubMed
    1. Blemker SS, Delp SL. Rectus femoris and vastus intermedius fiber excursions predicted by three-dimensional muscle models. J Biomech. 2006;39:1383–1391. - PubMed

Publication types

LinkOut - more resources