iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://pubmed.ncbi.nlm.nih.gov/17389923
A Bayesian perceptual model replicates the cutaneous rabbit and other tactile spatiotemporal illusions - PubMed Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2007 Mar 28;2(3):e333.
doi: 10.1371/journal.pone.0000333.

A Bayesian perceptual model replicates the cutaneous rabbit and other tactile spatiotemporal illusions

Daniel Goldreich  1
Affiliations

A Bayesian perceptual model replicates the cutaneous rabbit and other tactile spatiotemporal illusions

Daniel Goldreich. PLoS One. .

Abstract

Background: When brief stimuli contact the skin in rapid succession at two or more locations, perception strikingly shrinks the intervening distance, and expands the elapsed time, between consecutive events. The origins of these perceptual space-time distortions are unknown.

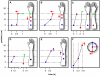
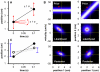
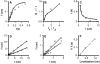
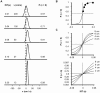
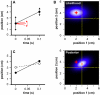
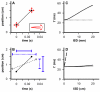
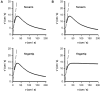
Methodology/principal findings: Here I show that these illusory effects, which I term perceptual length contraction and time dilation, are emergent properties of a Bayesian observer model that incorporates prior expectation for speed. Rapidly moving stimuli violate expectation, provoking perceptual length contraction and time dilation. The Bayesian observer replicates the cutaneous rabbit illusion, the tau effect, the kappa effect, and other spatiotemporal illusions. Additionally, it shows realistic tactile temporal order judgment and spatial attention effects.

Conclusions/significance: The remarkable explanatory power of this simple model supports the hypothesis, first proposed by Helmholtz, that the brain biases perception in favor of expectation. Specifically, the results suggest that the brain automatically incorporates prior expectation for speed in order to overcome spatial and temporal imprecision inherent in the sensorineural signal.

PubMed Disclaimer

Conflict of interest statement

Competing Interests: The author has declared that no competing interests exist.

Figures

Figure 1
Figure 1
Tactile length contraction (A–E) and time dilation (F) illusions. Actual stimulus sequences (plotted points) evoke illusory perceived sequences (positions on forearms in A–E; clock times in F). Colored arrows in panels A, B, E, and F indicate direction of perceptual effect (arrow at right) caused by adjustment to corresponding stimulus location or time (arrow at left). (A) Rabbit illusion . The two intermediate taps, separated by short temporal interval (rapid movement), are perceptually displaced towards one another. (B) Classic tau effect , . The more rapidly traversed of two equal distances is perceived as shorter. (C) Tau effect with two-arm comparison . Stimulus parameters were adjusted to reach the point of subjective equality, at which the greater distance (faster movement) is perceived equal to the shorter distance (slower movement). (D) Perceptual merging . At very rapid velocities, the perceived locations of the two taps merge to a single point. The velocity required to accomplish perceptual merging increases with tap separation. (E) Two-stimulus distance estimation . When inter-stimulus distance is increased at fixed inter-stimulus time, perceived distance both underestimates, and grows with, actual distance. (F) Kappa effect . When inter-stimulus distance is increased at fixed inter-stimulus time, perceived inter-stimulus time overestimates actual time. Stimulus parameters were adjusted to reach the point of subjective equality, at which perception dilates the temporal interval defined by the greater distance (faster movement) to equal the slightly longer temporal interval defined by the smaller distance (slower movement).
Figure 2
Figure 2
Basic Bayesian observer. (A) Two stimuli touch skin in rapid succession (filled circles). Reflecting sensorineural imprecision, each stimulus evokes a Gaussian likelihood function, centered on its actual position, with spatial standard deviation σs (vertical arrows: ±1 σs). The observer considers slow movement most probable a priori, adopting a Gaussian prior probability distribution for velocity, centered on zero, with standard deviation σv (slopes: ±1 σv). (B) Candidate trajectories, represented by first stimulus position and velocity (left column) or, equivalently, first and second stimulus positions (right). Intensity represents probability. Prior (top) x likelihood (middle) ∝ posterior probability (bottom). The actual trajectory (red crosshairs in all panels) occupies the position of maximal likelihood, but its velocity exceeds prior expectation. Perception (mode of posterior; red dot) is a compromise between reality and expectation. (C) Actual (filled circles, solid line) and perceived (open circles, dashed line) trajectories. Perceived ISD (l' = 0.67 cm; dotted bar) underestimates actual ISD (l = 2 cm; solid bar), and perceived velocity (v' = 6.7 cm/s) underestimates actual velocity (v = 20 cm/s).
Figure 3
Figure 3
Human data from five studies (symbols) and basic Bayesian observer's performance on the same tasks (solid curves in A–E). For each study, the value of λ was chosen to minimize the mean-squared error between model and human performance. (A) Rabbit on forearm (Fig. 1A) . R2: 0.80. λ: 12.7/s. (B) Two-arm tau effect (Fig. 1C) . x-axis: IST ratio ( pair 1/pair 2 ). Pair 1 ISTs (from left to right) were 0.2, 0.35, 0.5, 0.65, and 0.8 s; pair 2 IST = 1.0 s-pair 1 IST. y-axis: ISD ratio ( pair 2/pair 1 ) that resulted in equality of perceived ISDs ( pair 1 l' = pair 2 l' ). Pair 1 ISD was fixed at 10 cm. R2: 0.95. λ: 9.4/s. (C) Perceptual merging experiment (Fig. 1D) . R2: 0.92. λ: 4.2/s. (D) Two-stimulus distance estimation for longitudinally separated stimuli on forearm (circles) and horizontally separated stimuli on forehead (crosses) at 0.24 s IST (Fig. 1E) . Forearm R2: 0.94. Forehead R2: 0.90. Forearm λ: 4.9/s. Forehead λ: 10.5/s. (E) Two-stimulus distance estimation for longitudinally separated taps to the index finger . Circles: 1.1 s IST; crosses: 26 ms IST. R2 (1.1 s): 0.94, R2 (26 ms): 0.90. λ: 85.1/s. (F) Point localization accuracies for finger, forehead, and forearm plotted against 1/λ (dashed line). R2: 0.99.
Figure 4
Figure 4
Temporal order judgments of the basic Bayesian observer. (A) Posterior probability distributions for velocity, for 4 cm ISD and 0.01 s-0.30 s ISTs, obtained by integrating across the corresponding 2-dimensional posterior probability distributions (e.g., Fig. 2B, lower left). A second integration finds the area under each curve to the right of zero, P(v>0). (B) TOJ curve, plotting P(v>0) from (A), and additional values for the opposite movement direction (negative x-axis), against IST. (C) Upper panel: TOJ curves for 2 cm to 8 cm ISD, and −80 ms to 80 ms IST. Lower panel: The same curves plotted with y-axis probit (cumulative normal probability) coordinate spacing. As with human TOJ curves plotted in this manner –, these curves are linear. Model parameter values used for all panels: σs, 1 cm; σv , 10 cm/s.
Figure 5
Figure 5
Basic Bayesian observer with directed spatial attention. (A) Plot of the same stimuli (filled circles) shown in Figure 2. Attention directed to the location of the second stimulus lowers σs2 and increases σs1 (vertical arrows: ±1 σs). The observer considers slow trajectories most probable a priori (red slopes: ±1 σv). (B) Likelihood and posterior distributions in positional trajectory space (The prior is identical to that shown in Fig. 2). The oval-shaped likelihood distribution results because σs1≠σs2. The mode of the posterior (red dot) shows that the perceived location of the first stimulus has shifted more than that of the second stimulus, relative to their actual locations (red crosshairs). (C) Actual (filled circles, solid line) and perceived (open circles, dashed line) trajectories. The midpoint of the perceived trajectory has shifted towards the location of stimulus 2 by 0.3 cm relative to the actual trajectory midpoint. Model parameter values used for all panels: σs1, 1.23 cm; σs2, 0.70 cm; σv , 10 cm/s.
Figure 6
Figure 6
Full Bayesian observer. (A) Two stimuli (filled circles) touch the fingertip in rapid succession. The observer is uncertain as to stimulus location (vertical arrows: ±2 σs for clarity) and time of occurrence (horizontal arrows: ±1 σt ), and considers slow movement most probable a priori (inset slopes: ±1 σv). (B) Actual (filled circles, solid line) and perceived (open circles, dashed line) trajectories. Perception underestimates ISD (l' = 0.64 cm <l = 1 cm; vertical bars) and overestimates IST (t' = 40 ms>t = 26 ms; horizontal bars). (C) Perceived IST on finger dilates as ISD increases from 0–20 mm (solid line; kappa effect). The basic observer, by contrast, perceives IST veridically (dotted line). (D) Time dilation of full observer on forearm for 0–20 cm ISD (solid line). Perception on finger (C) is reproduced for comparison (dashed line). All panels: IST, 26 ms; σt, 5 ms; σs (finger), 1 mm; σs (forearm), 1 cm; σv, 4.7 cm/s.
Figure 7
Figure 7
Human data from five studies and full Bayesian observer's performance on the same tasks. The same five data plots shown in Fig. 3 (symbols) are reproduced here along with performance of the full model (curves). σt was fixed at 5 ms, σs set to 1 cm (forearm) or 0.1 cm (finger), and the value of λ adjusted in each case to minimize the mean-squared error between model and human performance. The performance of the full model is very similar to that of the basic model (compare to Fig. 3A–E). However, perception on the finger at 26 ms IST (crosses in E) is better-matched by the nonlinear performance of the full model (arrow; R2: 0.95) than by the linear performance of the basic model (R2: 0.90; compare Fig. 3E).
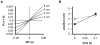
Figure 8
Figure 8
Temporal order judgment and spatial attention effects of the full Bayesian observer. (A) TOJ curves for 2 cm to 8 cm ISD, and −80 ms to 80 ms IST, plotted with y-axis probit coordinate spacing (compare to Fig. 4C lower). Model parameter values used: σs, 1 cm; σv, 10 cm/s; σt, 5 ms. (B) Actual (filled circles, solid line) and perceived (open circles, dashed line) trajectories when the full observer directs attention to the location of the second stimulus (compare to Fig. 5C). Model parameter values used: σs1, 1.23 cm; σs2, 0.70 cm; σv, 10 cm/s; σt, 5 ms.
Figure 9
Figure 9
Velocity perception of the Bayesian observer models. Perceived velocity, v', is plotted against real velocity, v, for the basic (A) and full (B) Bayesian observer models, on both forearm (top panels) and fingertip (bottom panels). In all cases, real velocity was increased by reducing IST at fixed ISD (4 cm for forearm; 4 mm for fingertip). (A) Basic observer: Perceived velocity, v' = l'/t, was derived from Equation 3. Real velocity v* = 28.28 cm/s (Equation 4) results in peak perceived velocity v'max = 14.14 cm/s (Equation 5). (B). Full observer: Perceived velocity, v' = l'/t', was determined from Equations 2 and 16, with σt set to 5 ms. Dotted lines in all panels: x = y. (A) and (B): σs was set to 1 cm (forearm) or 1 mm (finger), and σv to 10 cm/s.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Darian-Smith I, Kenins P. Innervation density of mechanoreceptive fibres supplying glabrous skin of the monkey's index finger. J Physiol. 1980;309:147–155. - PMC - PubMed
    1. Johansson RS, Vallbo AB. Tactile sensibility in the human hand: relative and absolute densities of four types of mechanoreceptive units in glabrous skin. J Physiol. 1979;286:283–300. - PMC - PubMed
    1. Wassle H, Grunert U, Rohrenbeck J, Boycott BB. Retinal ganglion cell density and cortical magnification factor in the primate. Vision Res. 1990;30:1897–1911. - PubMed
    1. Johnson KO, Phillips JR. Tactile spatial resolution. I. Two-point discrimination, gap detection, grating resolution, and letter recognition. J Neurophysiol. 1981;46:1177–1192. - PubMed
    1. Weinstein S. The skin senses : proceedings. Springfield, Ill.: Thomas; 1968. Intensive and extensive aspects of tactile sensitivity as a function of body part, sex, and laterality. pp. 195–222.