Lente
Esta página ou seção foi marcada para revisão devido a incoerências ou dados de confiabilidade duvidosa. |

Lente é um elemento que atua por refração, introduzindo descontinuidades no meio em que a luz se propaga inicialmente, e que reconfigura a distribuição da energia transmitida, independente da frequência da luz, isto é, tanto no ultravioleta como no domínio óptico, infravermelho, micro-ondas, ondas, rádio ou mesmo ondas acústicas. A forma da lente irá depender do tipo de reformatação da onda luminosa que se deseja.
Segundo Isaac Newton, “os raios homogêneos que partem de vários pontos de qualquer objeto e incidem perpendicularmente ou quase perpendicularmente sobre qualquer plano refletor ou refrator ou superfície esférica divergem depois disso de tantos outros pontos ou são paralelos a tantas outras retas ou convergem para tantos outros pontos com precisão ou sem erro notável. E o mesmo acontece se os raios são refletidos ou refratados sucessivamente por dois ou três ou mais superfícies esféricas planas ou esféricas.
A causa da reflexão não é o choque da luz com as partes sólidas ou impenetráveis dos corpos, como se acredita. Os corpos refletem e refratam a luz em virtude de uma mesma força, exercida variadamente em variadas circunstâncias. Os estados de fácil reflexão são os retornos da tendência de qualquer raio para ser refletido; aos de sua tendência para ser transmitido, estados de fácil transmissão; e ao espaço que se sucede entre cada retorno e o retorno seguinte, intervalo de seus estados.
O motivo pelo qual as superfícies de todos os corpos espessos transparentes refletem parte da luz que sobre eles incide e refratam o restante é que alguns raios, em sua incidência, estão em estados de fácil reflexão e outros em estados de fácil transmissão. Essas superfícies dos corpos transparentes que refratam o raio mais fortemente se ele está num estado de refração, refletem-no mais facilmente se ele está num estado de reflexão.” [1]
Existem 6 tipos de lentes delgadas compatíveis com essa definição: a)biconvexa; b)plano-convexa; c)côncavo-convexa; d)bicôncava; e)plano-côncava; f)convexo-côncava.

Uma lente que faz com que os raios luminosos inicialmente paralelos ao eixo central se aproximem do eixo é chamada de lente convergente; uma lente que faz com que os raios se afastem do eixo central é chamada de lente divergente. [2]
Uma lente pode produzir uma imagem de um objeto porque é capaz de desviar os raios luminosos, mas só é capaz de desviar os raios luminosos se tiver um índice de refração diferente do índice de refração do meio. [2]
Como no caso dos espelhos planos e esféricos, para a formação de imagens pelas lentes, é necessário, pelo menos, que de cada ponto do objeto que se deseja localizar a imagem emerjam dois raios na direção da lente. [3]
História
[editar | editar código-fonte]Não se tem certeza de quando foram criadas as primeiras lentes, mas já no século VIII a.C. existia um cristal de rocha com propriedades de ampliação da imagem. No entanto, foi só no século XIII que esse cristal passou a ser conhecido e utilizado, surgindo então os primeiros óculos.
Desde a sua origem esse instrumento óptico tem sido muito utilizado. Na época, logo após sua criação, houve uma rápida popularização, de modo que muitos pesquisadores começaram a fazer combinações entre lentes para a aplicação nos chamados instrumentos ópticos, como microscópios, telescópios. [4]
Refração em superfícies asféricas
[editar | editar código-fonte]Johannes Kepler foi quem pela primeira vez sugeriu a utilização de superfícies cônicas em lentes e espelhos, mas dificilmente poderia aprofundar a sua ideia sem o auxílio da Lei de Snell. Ainda com base nessa lei e na sua própria Geometria Analítica, René Descartes pode estabelecer as bases teóricas da óptica das superfícies asféricas.
As lentes mais espessas no eixo do que na borda são chamadas de lentes convexas ou convergentes (essas lentes convergem os raios luminosos incidentes se o índice de refração da lente for maior do que o do meio no qual ela está envolvida) e são responsáveis pelo aumento da convergência do feixe incidente.
As lentes mais finas no eixo do que nas bordas são chamadas de lentes côncavas ou divergentes (aqui também, essas lentes divergem os raios luminosos incidentes se o índice de refração da lente for maior do que o do meio no qual ela está envolvida) e aumentam a divergência dos raios luminosos em relação ao eixo central. Quando iluminadas por feixes colimados (de raios paralelos) dão origem a feixes divergentes.
Quando se faz incidir um feixe colimado numa lente convergente (ou divergente), o ponto para o qual o feixe converge (ou do qual ele parece divergir) é o ponto focal da imagem na lente.
Elementos ópticos, lentes ou espelhos, com dioptrias que não são planos nem esféricos, são conhecidos como asféricos. Embora seu funcionamento seja fácil de compreender e realizem muito bem certas funções, as lentes asféricas são bastante difíceis de serem produzidas com precisão. As primeiras lentes produzidas em grande quantidade com precisão foram utilizadas nas máquinas fotográficas Kodak, em 1982. Atualmente as lentes asféricas são utilizadas com frequência para corrigir erros de formação de imagem em sistemas ópticos complexos, como telescópios, projetores, sistemas de reconhecimento.
Refração em superfícies esféricas
[editar | editar código-fonte]Duas peças de material com superfícies esféricas, uma côncava e outra convexa, ambas com o mesmo raio de curvatura, encaixam perfeitamente uma na outra, seja qual for a sua orientação relativa. Quando dois objetos aproximadamente esféricos com a curvatura adequada, sendo um deles um utensílio de polimento e o outro um disco de vidro, separados por um abrasivo, são friccionados um contra o outro com movimentos aleatórios, os pontos salientes desaparecem e as superfícies tornam-se cada vez mais esféricas com o desgaste.
Atualmente, a maior parte das lentes de qualidade que se utilizam possuem superfícies esféricas. Estas superfícies permitem a formação de imagens de objetos extensos com luz não necessariamente monocromática. Os erros de formação de imagens, ou aberrações, são inevitáveis e estão sempre presentes, mas a tecnologia atual permite construir sistemas de lentes esféricas de alta qualidade, com aberrações controladas ate o limite da difração.
Em 1841, Gauss construiu uma análise da formação de imagens, conhecida como óptica Gaussiana, paraxial ou de primeira ordem. A óptica Gaussiana é o instrumento teórico básico que tem permitido a síntese de sistemas ópticos. Num sistema óptico devidamente corrigido, uma onda esférica incidente emerge com uma forma aproximadamente esférica. À medida que a qualidade do sistema aumenta, cada vez mais aplicável é a teoria da primeira ordem. Os desvios relativos ao comportamento paraxial constituem uma medida conveniente da qualidade de um sistema óptico real.
Lentes delgadas
[editar | editar código-fonte]As lentes podem ter uma grande variedade de formas. Uma lente é normalmente um sistema óptico constituído por dois ou mais dioptros um dos quais pelo menos é curvo. As superfícies não planas tem os respectivos centros de curvatura sobre um eixo comum. São quase sempre esféricas e frequentemente revestidas de filmes dielétricos que permitem controlar a sua transmissão.
Uma lente constituída por um só elemento (dois dioptros) é uma lente simples. Uma lente composta é constituída por vários elementos (dioptros).
As lentes podem ser classificadas de acordo com a sua espessura, sendo as convexas, convergentes ou positivas as lentes mais espessas no centro e que tendem a fazer diminuir o raio de curvatura das frentes de onda incidentes (pressupondo-se que o índice da lente é superior ao do meio em que esta se encontra).


Por outro lado, as lentes côncavas, divergentes ou negativas são mais finas no centro, e facilitam um avanço mais rápido da frente de onda nessa zona, aumentando o raio de curvatura e fazendo-a divergir mais acentuadamente.


Dioptro plano
[editar | editar código-fonte]O conjunto constituído por dois meios transparentes e a interface entre eles recebem o nome de dioptro. A forma da superfície de separação entre os meios, superfície dióptrica, caracteriza o tipo de dioptro: plano, esférico, cilíndrico.
Tomando como base os meios ar-água de um lago em repouso, por exemplo. Inicialmente o objeto encontra-se submerso na água (meio mais refringente) e o observador encontra-se fora dela, no ar (meio menos refringente). Sabemos que do objeto submerso partem raios de luz em todas as direções; sabemos também que esses raios sofrem refração na superfície da água e chegam aos olhos do observador.
A imagem do objeto é definida como virtual por ser formada pela intersecção dos prolongamentos dos raios refratados. A imagem é formada no mesmo meio em que o objeto está. Tanto a imagem quanto o objeto estão sobre a mesma reta perpendicular em relação a superfície dióptrica, portanto a imagem forma-se mais próxima da superfície da água.[5]


- Equação das lentes delgadas
- Fórmula de Gauss para lentes delgadas
A distância a qual se forma a imagem é aproximadamente igual a f. Quando a lente se aproxima de so,si deve ser ajustado de modo a manter sempre a nitidez da imagem e si vai, portanto, aumentar. Quando so se aproxima de f a imagem do filamento só se obtém com afastamento significativo do alvo. Para so < f não se consegue obter mais que uma mancha, seja qual for a distância a que se intersecta o feixe de raios divergentes – a imagem é agora virtual. [6]
Construção de imagens
[editar | editar código-fonte]Aqui três coisas são importantes: objetos, lentes, imagens. As lentes podem fazer com que os objetos tenham algumas características diferentes dos objetos que a geraram.
Para entender quais as características de uma imagem gerada por uma lente, deve-se conhecer o comportamento de alguns raios de luz, que serão chamados de principais.
- Raios principais para lentes convergentes
Um raio de luz que se propaga paralelamente ao eixo principal da lente, sofre refração passando pelo foco da imagem.
Um raio de luz que se propaga pelo foco objeto da lente, sofre refração saindo paralelamente ao eixo principal da lente.
Um raio de luz que incide sobre seu próprio centro óptico, irá refratar sem sofrer desvio algum.
- Raios principais para lentes divergentes
Um raio de luz que se propaga paralelamente ao eixo principal da lente sofre refração, e o prolongamento do raio refratado vai passar sempre pelo foco da imagem.
Um raio de luz que se propaga de tal forma que o seu prolongamento passe pelo Fo, irá refratar paralelamente ao eixo principal da lente.
Um raio de luz que incide sobre o seu centro óptico, irá refratar sem sofrer desvio algum.
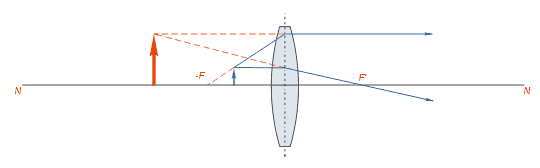
Ao apresentar as características das lentes foi considerado o princípio de construção da imagem de um ponto luminoso no foco da lente. Raios incidem sobre a lente na esquerda, passam para trás pelo foco, refletindo no lado direito - através do ponto focal da frente.

A construção das imagens de lentes de objetos com um certo tamanho e forma, é obtido como se segue: digamos a linha AB é o objeto localizado a alguma distância da lente, muito acima da sua distância focal. A partir de cada ponto do objeto através da lente sairão inúmeros raios, dos quais, por motivos de clareza, a figura mostra, esquematicamente, o curso de apenas três raios.
Três raios que emanam de um ponto A, irão passar através da lente e se cruzarão no ponto de fuga formando uma imagem. A imagem resultante será real e invertida.
Neste caso, a imagem obtida no foco conjugado num plano focal FF, mais afastada do plano focal principal F'F ', que se estende paralelamente a um foco principal.
A seguir estão os diversos casos de formação de imagem de um objeto colocado em diferentes distâncias da lente.
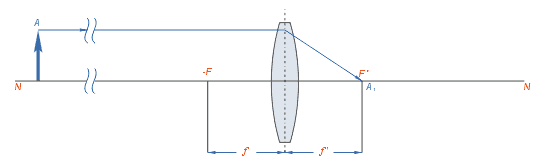
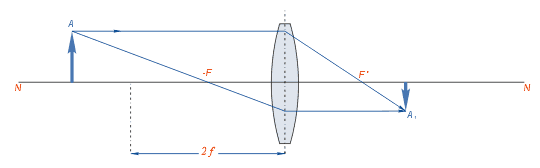
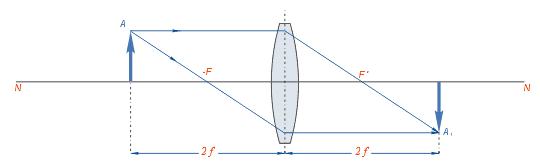

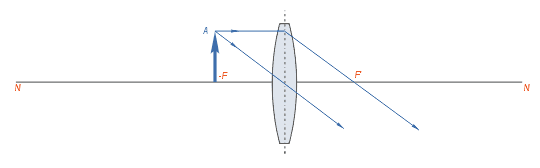
Distâncias focais
[editar | editar código-fonte]Método de Bessel
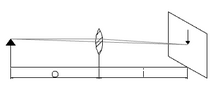
[editar | editar código-fonte]Podemos encontrar a distância focal de uma lente convergente utilizando o Método de Bessel, batizado em homenagem à Friedrich Wilhelm Bessel, matemático alemão. O método consiste em utilizar um objeto, um anteparo (onde a imagem será formada) e a própria lente da qual queremos descobrir o foco. Para uma distância fixa "A" e duas posições diferentes da lente separadas por uma distância "D", Bessel provou que a distância focal se dá pela seguinte fórmula:

Como mostra a figura ao lado, devemos mover a lente até acharmos as duas posições em que a imagem do objeto se tornará nítida e aplicarmos essas medidas.
Para a lente na primeira posição temos (a partir da fórmula de Gauss):
(1)
E na segunda:
Considerando as equações acima simétricas em relação a P1 e P2, para uma única solução de f, devemos ter:
Substituindo na equação 1 e fazendo algumas manipulações algébricas chegamos à:
E finalmente à fórmula do Método de Bessel.
Pontos conjugados
[editar | editar código-fonte]Utilizamos a, já citada, fórmula de Gauss e com o auxílio novamente de um objeto e um anteparo, medimos a distância O do objeto até a lente e I da lente até a imagem formada no anteparo. Como se trata de um procedimento experimental é importante que se repita o processo algumas vezes com distâncias diferentes para uma maior precisão no resultado.
Lentes divergentes
[editar | editar código-fonte]
O processo para se determinar a distância focal de lentes divergentes é um pouco mais complexo[7]. É preciso um objeto virtual (mostrado tracejado na figura) obtido através de uma lente convergente. Para certa posição do objeto, localize e anote a posição i da imagem (objeto virtual) no anteparo e a distância da imagem real da lente convergente i.. A seguir coloque (como mostra a figura) uma lente divergente entre a lente convergente e o anteparo. A posição da imagem real dada pela lente convergente (tracejada) será a posição do objeto virtual para a lente divergente. Localize a imagem da lente divergente mudando a posição do anteparo (e da lente divergente caso seja preciso) para um ponto diferente (anteparo com linhas contínuas na figura), e determine a distância i' da imagem da lente divergente. Meça também a distância o' entre o objeto virtual e a lente divergente.
Aplicando i' e o' na fórmula de Gauss podemos determinar o foco da lente divergente.
Aplicações
[editar | editar código-fonte]Lente de aumento simples
[editar | editar código-fonte]O olho humano normal só é capaz de focalizar uma imagem de um objeto na retina se a distância entre o objeto e o olho for maior que a de um ponto conhecido como ponto próximo. Quando o objeto está a uma distância menor do que a do ponto próximo a imagem na retina se torna indistinta.
A posição do ponto próximo normalmente varia com a idade. Quando objeto está a uma distância menor que o ponto próximo ele não está mais em foco, ou seja, não pode mais ser visto com nitidez. É possível tornar a imagem novamente nítida observando o objeto através de uma lente convergente. Com o uso da lente a imagem estará mais distante do olho do que o ponto próximo, pode ser vista com mais nitidez.
A ampliação angular de uma lente de aumento simples é definida como a razão entre o ângulo ocupado pela imagem produzida pela lente e o ângulo ocupado pelo objeto quando o objeto se encontra nas proximidades do ponto próximo do observador.[8]
Microscópio composto
[editar | editar código-fonte]É formado por uma objetiva (a lente mais próxima do objeto) e uma ocular (a lente mais próxima do olho). Este instrumento é usado para observar pequenos objetos que estão muitos próximos da objetiva.
A distância entre as lentes é ajustada para que a imagem (real, aumentada e invertida) produzida pela objetiva fique um pouco mais próxima da ocular.
Como a distância entre a imagem e a ocular é ligeiramente menor que a distancia focal, a ocular se comporta como uma lente de aumento simples, produzindo uma imagem virtual, aumentada e invertida, que é a imagem observada pelo operador do instrumento.
A amplificação lateral total conseguida pelo instrumento é o produto da amplificação produzida pela objetiva e pela amplificação angular produzida pela ocular.[2]
Telescópio
[editar | editar código-fonte]Lentes rudimentares escavadas na ilha de Creta datam de 2000 a.C. Lentes e óculos já eram usados desde cerca de 1350, e a maioria dos historiadores aceita que o primeiro telescópio foi construído pelo fabricante de óculos holandês Hans Lippershey (1570-1619), que em 1608 inventou um instrumento para olhar coisas a distância, constituído por um tubo com uma lente em cada extremidade.
Em maio de 1609, Galileo construiu seu primeiro telescópio, com aumento de 3 vezes; aprimorou-o rapidamente e em novembro do mesmo ano já tinha um telescópio com aumento de 20 vezes, muito mais potente que qualquer outro existente na época. Foi com esse instrumento que ele iniciou os estudos da astronomia moderna. Porém não cabe a Galileo o crédito da invenção do telescópio.
O telescópio usado por Galileo era composto de uma lente côncava e uma lente convexa. Johannes Kepler (1571-1630), no seu livro Dioptrice publicado em 1611, explicou por que seria melhor construir um telescópio com duas lentes convexas, como se usa atualmente.
Em 1668, Isaac Newton (1643-1727) construiu um telescópio refletor que inspirou os usados atualmente em observatórios profissionais, com um espelho côncavo no fundo do tubo, um pequeno espelho plano para desviar a luz perpendicularmente para fora do tubo, e uma lente ocular convergente.
Guillaume Cassegrain (1625-1712) propôs em 1672 usar um espelho convexo secundário para convergir a luz para um buraco no centro do espelho principal do telescópio, mas esse design não podia ser feito naquela época. A maioria dos telescópios modernos tem foco Cassegrain. O espelho secundário pode ser deslocado ao longo do eixo do tubo, mudando a distância focal.
A maior lente que se pode construir atualmente tem aproximadamente 1 metro de diâmetro, pesa meia tonelada, e deforma-se devido ao seu próprio peso, já que não pode ser apoiada por trás, como um espelho.
A sensibilidade de um telescópio aumenta com o tamanho da área coletora, e portanto com o quadrado do diâmetro da lente ou espelho que recebe a luz. Por isso astrônomos tentam construir telesópios cada vez maiores, quanto mais sensível um telescópio, menores e mais distantes serão os objetos que ele conseguirá mostrar. Os telescópios tradicionais da Terra podem enxergar objetos da ordem de 1 segundo de arco ou maiores (60 segundos de arco valem um minuto de arco e 60 minutos de arco valem um grau). Com ótica ativa, que modifica rapidamente a forma dos espelhos para compensar a cintilação causada pela turbulência da atmosfera, este limite decresce para aproximadamente 0,3 segundos de arco.
Em 1948 foi inaugurado o telescópio Hale, de Monte Palomar, na Califórnia, com um espelho primário de 5,08 metros de diâmetro, considerado o maior do mundo por três décadas. Desde 1990 os maiores telescópios do mundo são o Keck I e II, idênticos, com espelhos de 10 metros de diâmetro cada, formados por mosaicos de espelhos menores.
Os telescópios modernos tem focos Ritchey-Chrétien, onde o pequeno espelho secundário do Cassegrain é substituído por outro de forma mais complexa, que permite a correção da imagem para um campo maior. Na verdade tanto o primário quanto o secundário são hiperbolóides neste sistema.
- Tipos de Telescópios
- Refratores: neles a luz é recebida por uma lente, que normalmente veda o tubo do telescópio. Seus formatos fechados protegem as lentes da poeira e reduzem a degradação da imagem causada por correntes de ar. Se as lentes forem boas, um refrator oferece imagens nítidas e de alto contraste. Normalmente exige um prisma ou espelho diagonal na ocular para tornar a observação mais confortável, porem isso torna a imagem espelhada.
- Refletores: usam um espelho côncavo ao invés de lentes para coletar a luz e focalizá-la. São também conhecidos como Newtonianos. Podem exigem mais cuidados e manutenção, já que o tubo é aberto, podendo cair poeira nos espelhos. Os espelhos precisam de ajustes ocasionais para mantê-los perfeitamente alinhados.
- Catadióptricos: também conhecidos como compostos, usam tanto lentes quanto espelhos para receber a luz. A versão mais popular é o Schmidt-Cassegrain, que surgiu no mercado na década de 70 e rapidamente conquistou seu lugar ao lado dos refratores e refletores, que já existiam há séculos.
A vantagem desse tipo de telescópio não está na performance visual, mas sim na portabilidade, conveniência e opções especiais tais como sistemas avançados de acompanhamento computadorizado. São excelentes telescópios fotográficos.
A desvantagem do telescópio é que a imagem formada será provavelmente um pouco menos nítida do que a imagem formada por um bom refletor de mesma abertura. Isso é mais perceptível quando se observa os planetas. Um espelho ou prisma diagonal é normalmente usado na ocular para oferecer uma posição de observação mais confortável (como nos refratores), e isso significa que a imagem que você vê fica de cabeça para baixo e espelhada. O mecanismo de focalização pode ser muito delicado e impreciso.[9]
Ver também
[editar | editar código-fonte]- Lente Objetiva
- Lentes condensadoras
- Lentes oftálmicas
- Lente gravitacional
- Lente de contacto
- Lente de Fresnel
- Lente multifocal
Referências
- ↑ NEWTON, Isaac, Óptica, 1ª edição
- ↑ a b c HALLIDAY, RESNICK & WALKER, Fundamentos de Física, vol. 4, 8 edição, cap. 34
- ↑ HECHT, Eugene. Óptica, 2 edição
- ↑ http://educador.brasilescola.com/estrategias-ensino/a-historia-das-lentes.htm
- ↑ http://www.brasilescola.com/fisica/dioptro-plano.htm
- ↑ http://www.portalsaofrancisco.com.br/alfa/lentes/lentes.php
- ↑ «11»
- ↑ HALLIDAY, RESNICK & WALKER, Fundamentos de Física, vol. 4, 8 edição, cap. 34
- ↑ http://www.portalsaofrancisco.com.br/alfa/telescopios/telescopios.php









