Abstract
Background
The World Health Organization (WHO) has recently developed a predictive model to evaluate the impact of preventive chemotherapy programmes to control the morbidity of soil-transmitted helminths (STH). To make predictions, this model needs baseline information about proportion of infections classified as low, moderate and high intensity, for each of the three STH species, however the epidemiological data available are often limited to prevalence estimates.
Methods
We re-analyzed available data of 19 surveys in 10 countries and parameterized the relationship between prevalence of STH infections and the proportion of moderate and heavy intensity infections.
Results
The equations derived allow feeding the WHO model with estimates of the proportion of the different classes of infection intensity when only prevalence data is available.
Keywords: Epidemiology, Soil Transmitted Helminths
Introduction
Soil-transmitted helminths (STH) are a group of intestinal nematodes composed by Ascaris lumbricoides (roundworms), Trichuris trichiura (whipworms), Necator americanus and Ancylostoma duodenale (hookworms). STH infections adversely affect nutritional status and impair cognitive processes [1]. The public health intervention recommended by World Health Organization (WHO) for the control of morbidity associated with STH infections is the periodic administration of the anthelmintic medicines (albendazole or mebendazole) in areas where prevalence of any STH infection equals or exceeds 20% [2–3]. This intervention is referred to as preventive chemotherapy and is currently implemented in 58 countries covering over 260 million children [4].
In order to facilitate the assessment of the performance of STH control activities, WHO recently developed a mathematical model [5] based on Markov methodology [6].
Briefly, for each STH species, the model is based on:
-
1-
The assignment of each individual in one of the four Condition States (CS) corresponding to the four classes of infection intensity defined by WHO [7]: zero eggs, infected at light intensity, infected at moderate intensity and infected at high intensity.
-
2-
The calculation of the transition probabilities (TP) for an individual in one class of intensity, to remain in the same class of intensity or to change class during one year period of implementation of the control programme. We assumed that the TP are constant over time.
This model predicts the changes in prevalence of STH infections occurring over time during a control programme by applying multiple times the TP to the new CS. Figure 1 provides a graphical representation of the model in the case of hookworms. By comparing changes occurring in the context of their programmes with the references generated by the model, programme managers can therefore assess the performance of activities implemented.
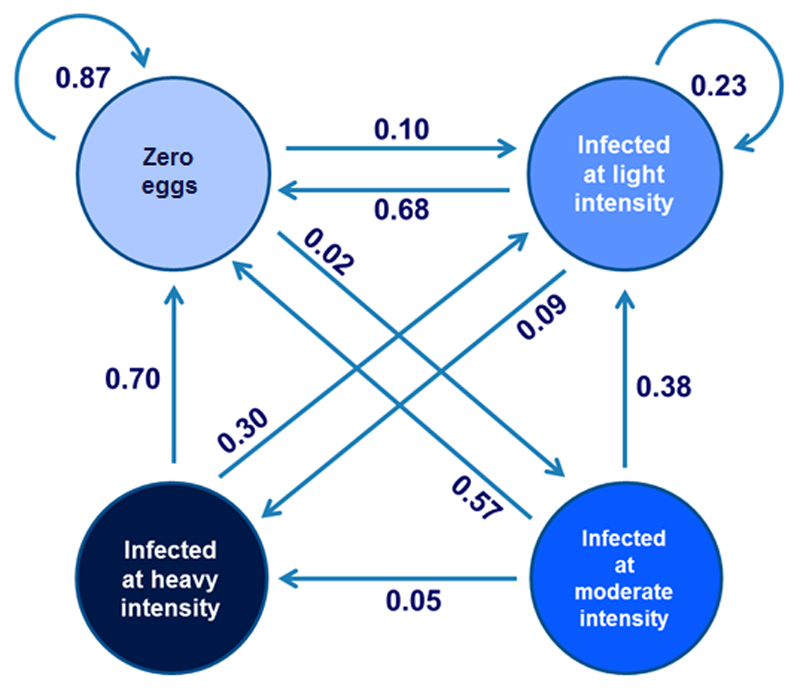
Figure 1.
Graphical representation of the Markov Model applied to hookworm infection data from Vietnam. The circles represent the four possible condition states (CS) and arrows represent the transition probabilities (TP) from one CS to another during one year of intervention.
For example in the case of individuals with “zero eggs” after the first year of intervention 87% of them remain not-infected, 10% became infected at light intensity and 2% became infected at moderate intensity.
While the model requires entering prevalence of each class of intensity for each relevant STH species, this information is not always available in the context of STH control programmes. The purpose of this paper is therefore to describe the relation between total prevalence and prevalence of infections of light, moderate and heavy intensity. Different authors have described the relationship between prevalence and intensity of infection [8,9] but this has never been done for the WHO classes of infection intensity [7].
Material and methods
We reviewed the available literature and contacted authors and other experts, requesting raw data from baseline surveys of STH infection. We limited ourselves to only baseline surveys – that is, surveys taken before the start of any control intervention. Our database included data from 18 surveys conducted in 10 countries: Afghanistan, Brazil, Cameroon, Cambodia, Ethiopia, Guinea, India, Lao PDR, Tanzania and Vietnam. The great majority (98%) of the data was collected from school-aged children. In total, the number of individual data analysed was 23 758, and the average number of individuals in each survey was 1 303 (range 350 – 3 436). Table 2 summarizes the sample size, diagnostic method applied and the population surveyed. Details of the different surveys are reported elsewhere [10–16].
Table 2.
Details of the surveys included in this study
| Country | Year | Sample size | Laboratory method used | Population surveyed | Data collected at | Reference |
|---|---|---|---|---|---|---|
| Guinea | 1997 | 1606 | Kato Katz | SAC | Baseline* | 10 |
| Tanzania (Zanzibar) | 2003 | 3436 | Kato Katz | SAC | Baseline* | 11 |
| Afghanistan | 2004 | 1000 | Kato Katz | SAC | Baseline* | 12 |
| Lao PDR | 2004 | 2885 | Kato Katz | SAC | Baseline* | 13 |
| Vietnam | 2008 | 367 | Kato Katz | WCBA | Baseline* | 14 |
| Brazil | 2011 | 350 | McMaster | SAC | Baseline* | 15 |
| Cambodia | 2011 | 1018 | McMaster | SAC | Baseline* | 15 |
| Cameroon | 2011 | 1483 | McMaster | SAC | Baseline* | 15 |
| Ethiopia | 2011 | 412 | McMaster | SAC | Baseline* | 15 |
| India | 2011 | 3274 | McMaster | SAC | Baseline* | 15 |
| Tanzania (Mainland) | 2011 | 508 | McMaster | SAC | Baseline* | 15 |
| Vietnam | 2011 | 1779 | McMaster | SAC | Baseline* | 16 |
| Brazil | 2012 | 980 | McMaster | SAC | Baseline* | 16 |
| Cambodia | 2012 | 1023 | McMaster | SAC | Baseline* | 16 |
| Cameroon | 2012 | 709 | McMaster | SAC | Baseline* | 16 |
| Ethiopia | 2012 | 693 | McMaster | SAC | Baseline* | 16 |
| Tanzania (Mainland) | 2012 | 698 | McMaster | SAC | Baseline* | 16 |
| Vietnam | 2012 | 1537 | McMaster | SAC | Baseline* | 16 |
| TOTAL | 23758 |
WCBA= Women of Child Bearing Age
SAC =School Age Children
Baseline*= before initiation of control activities
In 73% of the surveys (13/18) the parasitological laboratory method was the McMaster [17] and in the remaining cases the Kato Katz [18–19]. The two methods demonstrated a strong correlation especially in the classification of each infection in classes of intensity [20].
For each survey and each parasite we extracted from the available raw data:
the total prevalence of infection;
the prevalence of infection of light intensity
the prevalence of infection of moderate intensity;
the prevalence of infection of heavy intensity.
The data were recorded in Microsoft Excel (version 14.0) and imported into R (version 3.0.2) for further analysis.
Association between infection prevalence and infection intensity was estimated in a multinomial logistic regression (MLR). MLR is used to predict categorical placement in a dependent variable where more than two outcomes are possible, based on at least one independent variable [21]. In this study the three infection intensities represent mutually exclusive outcomes for infected individuals. Prevalence of each infection intensity in a population was measured as the probability of observing that intensity in a population given total infection prevalence. Conditional probabilities (proportion of individuals among the infected) were used to ensure that the prevalence of all three intensities sums to total prevalence. To derive the multinomial logit model, one of the three outcomes (in this case light intensity infection) is chosen as the reference outcome. Two independent binary logistic regression models are then run, one for each of the remaining two outcomes, moderate and heavy intensity. The regressand is the log risk ratio between the moderate (or heavy) intensity and light intensity infection. The regression model is shown in equation 1.
| (equation 1) |
Where
y = outcome in population i
k = categorical outcome (moderate or heavy intensity infection)
x = total prevalence in population i
r = reference outcome (light intensity)
Exponentiating the right hand side of the equation gives the risk ratio between moderate (heavy) and light intensity infection. The probability of moderate (heavy) infection is then derived by dividing the risk ratio by the probability of the light intensity infection, as presented in equation 2.
| (equation 2) |
The prevalence of light intensity is given by equation 3, derived from the fact that the prevalence of all three intensities must sum to one.
| (equation 3) |
Details on theory behind multinomial logistic regression can be found in the statistics literature [22].
Values were then converted to joint probabilities to present prevalence of intensity as a proportion of the total population. All studies were assigned equal weights when running the regressions. Results were compared to those obtained when studies were weighted by sample size.
Different transformations of total prevalence were considered for the best possible fit: total prevalence squared, the square root of total prevalence, the natural logarithm of total prevalence, and the gamma exponential and the logistic transformations of total prevalence. Other independent variables were also considered. The effect of income level on the prevalence of moderate and heavy intensity was considered by adding countries’ national Gross Domestic Product (GDP) per capita in constant US$ (2005 prices) at the time of each study.[23] GDP per capita could serve as a proxy for water and sanitation coverage and school attendance. Other variables, such as age of children tested were not taken into account as the lack of information would have further reduced the number of studies included.
Relative goodness of fit was measured using Akaike’s information criterion (AIC) [24]. AIC compares quality of a models taking into account model deviance and the number of parameters. Lower values indicate better fit. AIC was used to select the best-performing model. The results of the best-performing models are presented for each species of helminth in Table 3.
Table 3.
Statistical models predicting the prevalence of light, moderate and heavy intensity infections from total prevalence. Coefficients describe the relationship between the transformation of total prevalence f(x) and log of the relative risk between moderate or heavy infection and light infection ln[π(yi=k|xi)/π(yi=r|xi) (see equation 1 for details). Negative intercepts indicate that when total prevalence is zero, log of the risk ratio is negative. In other words the prevalence of light intensity infection is expected to be higher than the prevalence of moderate or heavy infection. Furthermore, please note that when total prevalence is 0, predicted prevalence is also 0 for all three infection intensities regardless of the intercept. This is achieved by regressing prevalence conditional on infection, then multiplying it by total prevalence to convert it to prevalence among the whole population. Coefficients for light infection are not included as light infection prevalence is derived from moderate and heavy regressions (see equations 2-3). se = standard error of coefficients; qlogis (total prevalence) = logistic transformation of total prevalence
| A. Lumbricoides | Hookworm | T. trichiura | ||||
|---|---|---|---|---|---|---|
| f(x) | qlogis(total prevalence) | qlogis(total orevalence) | qlogis(total prevalence) | |||
| Outcome | Moderate infection | Heavy infection | Moderate infection | Heavy infection | Moderate infection | Heavy infection |
| Coefficient | 0.5005658 | 0.7736967 | 0.4997493 | 0.7000658 | 0.471674 | 0.4993203 |
| (se coefficient) | [0.4891418] | [1.9563929] | [0.6744374] | [1.1064873] | [0.3380304] | [1.8711727] |
| Intercept | -0.5078976 | -2.8866398 | -2.885889 | -3.967145 | -1.589407 | -5.394194 |
| (se intercept) | [ 0.7403698] | [2.0053610] | [1.232455] | [2.165248] | [0.7698707] | [4.6762308] |
| pseudo-R2 | 0.08170531 | 0.1024159 | 0.1810675 | |||
McFadden’s pseudo R2 (pseudo-R2McFadden) value was used as an objective measure of goodness of fit [25]. It suggests the level of improvement over the null (intercept) model offered by the full model. The null model assumes that the proportion of infected individuals suffering from moderate and heavy infection does not vary with total prevalence. pseudo-R2McFadden ranges from 0 to1, but, unlike R2 in ordinary linear regression, values tend to be significantly lower: pseudo-R2McFadden between 0.2 and 0.4 indicate excellent fit [26].
MLR does not assume normality or homoscedasticity and so confidence intervals cannot be derived from standard error of parameters like in ordinary linear regression. We calculated the 99% prediction intervals of the regression line by bootstrapping. Each study was assigned 1000 random weights from a uniform distribution (0,1). We ran the regression model 1000 times, made 1000 predictions, and extracted the mean, 0.5th and 99.5th percentiles of these 1000 predictions, for the best estimate and 99% prediction interval. Sensitivity of the regression model to sample size was assessed by weighting the studies by sample size and re-running the regression. The prediction interval was obtained by multiplying the randomly assigned weights by sample size N.
The full list of R packages used in this analysis is referenced in appendix 1.
Results
The nine multinomial curves and the regression coefficients obtained from models with the lowest AIC are presented in figure 2 and in table 3. GDP per capita did not improve the predictive power of the models.
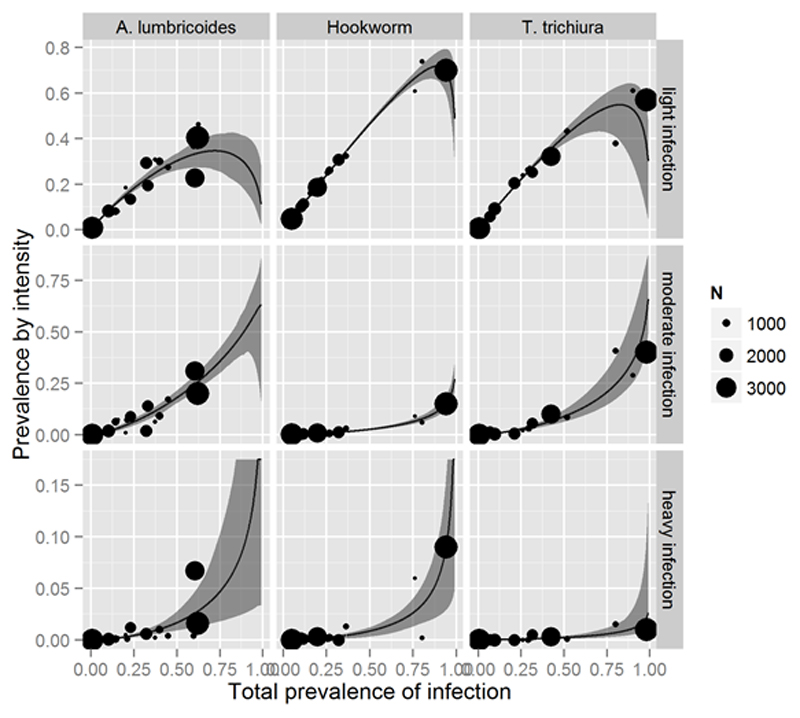
Figure 2.
Relationship between the prevalence of infection and prevalence by intensity.
Multinomial logistic regression with equal weights assigned to all studies; grey bands represent the 99% prediction intervals, size of points is proportional to study sample size.
The curves and coefficients allow us to estimate graphically or mathematically the prevalence of heavy, moderate and light intensity infections for each STH parasite, starting from the total prevalence of infection. Moderate and heavy infection are of particular value from the public health point of view because the individuals in these categories are the ones suffering more for the morbidity caused by these infections [3] and are the target of the STH control activities that aim at eliminating the infection as a public health problem (i.e. eliminating the morbidity) [27]. In the case of hookworm a prevalence of infection of 75% (0.75) graphically corresponds to a prevalence of about 7 % (0.07) of infection of moderate intensity and 2 % (0.02) of infection of heavy intensity. Using the appropriate transformation of total prevalence and the regression coefficients in table 3 one can use equations 1-3 to compute the more precise result of 6.4% and 2.7% respectively. A table of prediction values for all three helminths is presented in appendix 2. The predicted values for all three worms across the range of total prevalence between 0.01 and 1 is presented in appendix 3. Results for total prevalence greater than 58%, 94% and 98% for A. lumbricoides, hookworm and T. trichiura respectively should be interpreted with caution as they span beyond our dataset.
The standard errors of coefficients are provided in table 3. It is important to note that confidence intervals cannot be derived from these standard errors in the same way as ordinary linear regression because MLR does not assume normality or homoscedasticity. Prediction intervals were derived as described in the methods and are presented as shading in figure 2.
Table 2 quotes pseudo-R2McFadden values for each model. The T. trichiura model provides the best fit, with a pseudo-R2McFadden of 0.19 indicating a very good fit[26]. The models for A. lumbricoides and hookworm exhibit lesser goodness-of-fit. Parameters of the model derived by weighting studies by sample size were close to those in the original model. The table of coefficients and regression graphs are presented in appendix 3. Furthermore, predicted prevalence values were identical to the nearest percentage point to those obtained with the original, unweighted model.
Discussion
The results of this paper will allow national control programmes to estimate the prevalence of moderate-intensity infections and that of heavy-intensity infections starting from the total prevalence of each STH parasite. The parasite-specific equations will feed the STH Markov model [5] in cases when the prevalence of infections of light, moderate and heavy intensity is not known by programme managers. The changes in STH prevalence occurring throughout the duration of disease control activities can therefore be predicted, even though estimations obtained using this approximation will probably be less precise that those obtained when data on infection of moderate and heavy intensity are known.
There are limitations to the use of our results for this purpose. We utilized datasets in which the total prevalence and the prevalence of each class of intensity was evaluated with a single stool examination conducted either with the Kato-Katz method or with McMaster method. We recognize the low sensitivity of this methodology if compared with multiple samples of the same specimen and multiple days sampling of the same individual [28]. Measurement error in the independent variables can bias regression parameters towards zero, a statistical problem known as regression dilution. Several statistical techniques can be used to address regression dilution. However, the single sample is the method recommended by WHO [29] for surveys and is universally used in the monitoring and evaluation of deworming programmes; sensitivity of the tests used in our studies is therefore identical to that used in practice. Low sensitivity of the diagnostic technique will thus appear as noise, rather than bias, and correction for regression dilution is not recommended [30]. Bias will arise only if the models derived in this study are used to estimate the classes of intensity in programmes that use higher-sensitivity STH diagnostic techniques.
All the surveys utilized to calculate the curves and the equations for A. lumbricoides had a prevalence of infection inferior to 62% (see figure 2). We expect therefore that the estimations obtained with the corresponding equations to be less precise when the prevalence for A. lumbricoides is over that limit (i.e. over 62%). The model predicting intensity of T. trichiura has stronger predictive power than the remaining two models, which could be attributed to the sample size or factors not captured by the model. Nevertheless, all points appear to be within or in close proximity to the prediction intervals.
An additional observation of our study is that infections of heavy intensity are absent when the prevalence of any STH infection is less than 20%. This fact justifies WHO’s current recommendation of implementing preventive chemotherapy when prevalence of any STH is over 20%, as the focus of the WHO strategy is on control of morbidity, and morbidity is negligible if intensity of infection is low [2, 3]. Although the significance of the 20% threshold had been empirically recognized by the community of experts for a number of years [31], this is the first demonstration from a large sample of individuals.
Supplementary Material
Table 1.
Classes of intensity of STH infections
| STH specie | Uninfected (epg) | Light-intensity Infections (epg) | Moderate-intensity infections (epg) | Heavy-intensity infections (epg) |
|---|---|---|---|---|
| A. lumbricoides | 0 | 1 – 4 999 | 5 000 – 49 999 | >50 000 |
| T. trichiura | 0 | 1 – 999 | 1 000 – 9 999 | >10 000 |
| Hookworms | 0 | 1 – 1 999 | 2 000 – 3 999 | >4 000 |
epg = eggs per gram of faeces.
Acknowledgments
The paper was developed without any external funding and did not required ethical approuval. AM is the guarantor of thr paper.
References
- 1.Hall A, Hewitt G, Tuffrey V, de Silva N. A review and meta-analysis of the impact of intestinal worms on child growth and nutrition. Matern Child Nutr. 2008;4(Suppl 1):118–236. doi: 10.1111/j.1740-8709.2007.00127.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.WHO. Preventive chemotherapy in human helminthiasis: coordinated use of anthelminthic drugs in control interventions: a manual for health professionals and programme managers. Geneva: WHO; 2006. [Google Scholar]
- 3.Gabrielli AF, Montresor A, Chitsulo L, et al. Preventive chemotherapy in human helminthiasis: theoretical and operational aspects. Trans R Soc Trop Med Hyg. 2011;105:683–93. doi: 10.1016/j.trstmh.2011.08.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.WHO. Soil-transmitted helminthiases: number of children treated in 2012. Weekly epidemiological Record. 2014;89:133–140. [PubMed] [Google Scholar]
- 5.Montresor A, Gabrielli AF, Yajima A, Lethanh N, Biggs BA, Casey GJ, Thinh TT, Engels D, Savioli L. Prevalence Prediction of Soil Transmitted Helminth with Markov model: A case study in Vietnam. Transactions of the Royal Society of Tropical Medicine and Hygiene. 107:313–318. doi: 10.1093/trstmh/trt019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Howard RA. Dynamic Programing and Markov Processes. Cambridge, MI: Technology Press of the Massachusetts Institute of Technology; 1960. [Google Scholar]
- 7.WHO. Prevention and control of schistosomiasis and soil-transmitted helminthiasis. Report of a WHO Expert Committee; Geneva: WHO: 2002. [PubMed] [Google Scholar]
- 8.Anderson RM, May RM. Population dynamics of human helminth infections: control by chemotherapy. Nature. 1982;297:557–63. doi: 10.1038/297557a0. [DOI] [PubMed] [Google Scholar]
- 9.Bundy DA, Hall A, Medley GF, Savioli L. Evaluating measures to control intestinal parasitic infections. World Health Stat Q. 1992;45(2–3):168–79. [PubMed] [Google Scholar]
- 10.Montresor A, Urbani C, Camara B, Bha B, Albonico M, Savioli L. Enquete preliminaire a la mise en place d’un programme de santé scolaire en Guinée. Médecine Tropicale. 1997;57:294–298. [PubMed] [Google Scholar]
- 11.Albonico M, Bickle Q, Ramsan M, Montresor A, Savioli L, Taylor M. Efficacy of mebendazole and levamisole alone or in combination against intestinal nematode infections following repeated targeted mebendazole treatment in Zanzibar. Bulletin of the World Health Organization. 2003;81:343–52. [PMC free article] [PubMed] [Google Scholar]
- 12.Gabrielli AF, Ramsan M, Tsogzolmaa D, Bojang B, Naumann C, Khoshal MH, Ben-Ismail R, Connolly M, Montresor A, Savioli L. Soil-transmitted helminths and haemoglobin status among Afghan children in World Food Programme assisted schools. Journal of Helminthology. 2005;79:381–384. doi: 10.1079/joh2005316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Phommasack B, Saklokham K, Chanthavisouk C, Nakhonesid-Fish V, Strandgaard H, Montresor A, Shuey DA, Ehrenberg J. Coverage and cost of the school deworming targeting all primary schools in Lao PDR in 2007. Transactions of the Royal Society of Tropical Medicine and Hygiene. 2008;102:1201–1206. doi: 10.1016/j.trstmh.2008.04.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pasricha SR, Caruana SR, Casey GJ, Biggs BA, Phuc TO, Jolley D, Kingsland S, Tien NT, Macgregor L, Montresor A. Anaemia, iron deficiency, meat consumption and hookworm infection in women of reproductive age in northwest Vietnam. American Journal Tropical Medicine and Hygiene. 2008;78:375–81. [PMC free article] [PubMed] [Google Scholar]
- 15.Vercruysse J, Behnke JM, Albonico M, Ame SM, Angebault C, Bethony JM, Engels D, Guillard B, Hoa NTV, Kang G, Kattula D, et al. A multinational trial of the efficacy of albendazole against soil-transmitted helminth infections in children. PloS Negl Trop Dis. 2012;5:e948. doi: 10.1371/journal.pntd.0000948. (2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Levecke B, Montresor A, Albonico M, Ame SM, Behnke JM, Bethony JM, Noumedem CD, Engels D, Guillard B, Kotze A, Krolewiecki AJ, et al. Anthelminthic efficacy of single-oral dose 500 mg mebendazole in school children in six countries where soil-transmitted helminths are endemic: a meta-analysis. PLoS Negl Trop Dis. doi: 10.1371/journal.pntd.0003204. [in print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ministry of Agriculture, Fisheries and Food. Manual of veterinary parasitological laboratory techniques (Reference Book; 418) 3rd ed. London: Her Majesty's Stationery Office (HMSO); 1986. p. 160. [Google Scholar]
- 18.Katz N, Chaves A, Pellegrino J. A simple device for quantitative stool thick-smear technique in schistosomiasis mansoni. Rev Inst Med Trop São Paulo. 1972;14:379–400. [PubMed] [Google Scholar]
- 19.WHO. Laboratory methods in human parasitology. WHO; Geneva: 1991. [Google Scholar]
- 20.Levecke B, Albonico M, Ame SM, Bethony JM, Charlier J, Hoa NT, Kang G, Kattula D, Kotze A, McCartey J, Montresor A, et al. A Multinational Comparison of McMaster and Kato-Katz for the Detection and Quantification of Soil-Transmitted Nematode Infections in Public Health. PLoS NTD. 2011;5:e1201. [Google Scholar]
- 21.Long JS. Regression models for categorical and limited dependent variables. Thousand Oaks: SAGE; 1997. [Google Scholar]
- 22.Agresti . Categorical Data Analysis. 2nd edition. John Wiley & Sons, Inc; 2002. p. 273. Long JS in. [Google Scholar]
- 23.The World Bank. GDP per Capita (constant 2005 US$) | Data | Table. [Accessed August 28];2014 http://data.worldbank.org/indicator/NY.GDP.PCAP.KD.
- 24.Akaike Hirotugu. A new look at the statistical model identification. IEEE Transactions on Automatic Control. 1974;19(6):716–723. [Google Scholar]
- 25.McFadden D. Conditional Logit Analysis of Qualitative Choice Behavior. Frontiers in Econometrics. 1973:105–142. [Google Scholar]
- 26.Louviere JJ, Hensher AD, Swait DJ. Stated choice methods. New York: Cambridge University Press; 2000. [Google Scholar]
- 27.WHO. Eliminating Soil-transmitted helminthiasis as a public health problem in children. WHO; Geneva: 2012. [Google Scholar]
- 28.Knopp S, Mgeni AF, Khamis IS, Steinmann P, Stothard JR, Rollinson D, Marti H, Utzinger J. Diagnosis of soil-transmitted helminths in the era of preventive chemotherapy: effect of multiple stool sampling and use of different diagnostic techniques. PLoS Negl Trop Dis. 2008;2(11):e331. doi: 10.1371/journal.pntd.0000331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.WHO. Helminth control in school age children. A guide for control managers. second edition. WHO; Geneva: 2011. [Google Scholar]
- 30.Frost C, Thompson S. Correcting for regression dilution bias: comparison of methods for a single predictor variable. Journal of the Royal Statistical Society Series A. 2000;163:173–190. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.