Abstract
Biological networks have so many possible states that exhaustive sampling is impossible. Successful analysis thus depends on simplifying hypotheses, but experiments on many systems hint that complicated, higher-order interactions among large groups of elements have an important role. Here we show, in the vertebrate retina, that weak correlations between pairs of neurons coexist with strongly collective behaviour in the responses of ten or more neurons. We find that this collective behaviour is described quantitatively by models that capture the observed pairwise correlations but assume no higher-order interactions. These maximum entropy models are equivalent to Ising models, and predict that larger networks are completely dominated by correlation effects. This suggests that the neural code has associative or error-correcting properties, and we provide preliminary evidence for such behaviour. As a first test for the generality of these ideas, we show that similar results are obtained from networks of cultured cortical neurons.
Much of what we know about biological networks has been learned by studying one element at a time—recording the electrical activity of single neurons, the expression levels of single genes or the concentrations of individual metabolites. On the other hand, important aspects of biological function must be shared among many elements1-4. As a first step beyond the analysis of elements in isolation, much attention has been focused on the pairwise correlation properties of these elements, both in networks of neurons5-13 and in networks of genes14-16. But given a characterization of pairwise correlations, what can we really say about the whole network? How can we tell if inferences from a pairwise analysis are correct, or if they are defeated by higher-order interactions among triplets, quadruplets, and larger groups of elements? If these effects are important, how can we escape from the ‘curse of dimensionality’ that arises because there are exponentially many possibilities for such terms?
Here we address these questions in the context of the vertebrate retina, where it is possible to make long, stable recordings from many neurons simultaneously as the system responds to complex, naturalistic inputs17-20. We compare the correlation properties of cell pairs with the collective behaviour in larger groups of cells, and find that the minimal model that incorporates the pairwise correlations provides strikingly accurate but non-trivial predictions of the collective effects. These minimal models are equivalent to the Ising model in statistical physics, and this mapping allows us to explore the properties of larger networks, in particular their capacity for error-correcting representations of incoming sensory data.
The scale of correlations
Throughout the nervous system, individual elements communicate by generating discrete pulses termed action potentials or spikes21. If we look through a window of fixed time resolution Δτ, then for small Δτ these responses are binary—either the cell spikes (‘1’) or it doesn't (‘0’). Although some pairs of cells have very strong correlations, most correlations are weak, so that the probability of seeing synchronous spikes is almost equal to the product of the probabilities of seeing the individual spikes; nonetheless, these weak correlations are statistically significant for most, if not all, pairs of nearby cells. All of these features are illustrated quantitatively by an experiment on the salamander retina (Fig. 1), where we record simultaneously from 40 retinal ganglion cells as they respond to movies taken from a natural setting (see Methods). The correlations between cells have structure on the scale of 20 ms and we use this window as our typical Δτ.
Figure 1.
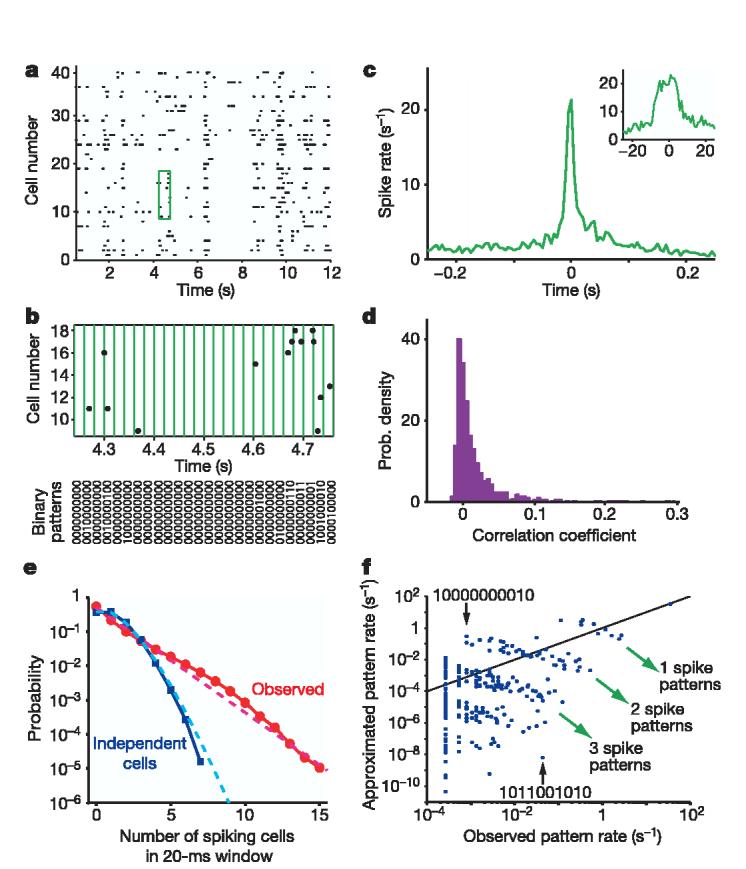
Weak pairwise cross-correlations and the failure of the independent approximation. a, A segment of the simultaneous responses of 40 retinal ganglion cells in the salamander to a natural movie clip. Each dot represents the time of an action potential. b, Discretization of population spike trains into a binary pattern is shown for the green boxed area in a. Every string (bottom panel) describes the activity pattern of the cells at a given time point. For clarity, 10 out of 40 cells are shown. c, Example cross-correlogram between two neurons with strong correlations; the average firing rate of one cell is plotted relative to the time at which the other cell spikes. Inset shows the same cross-correlogram on an expanded time scale; x-axis, time (ms); y-axis, spike rate (s−1). d, Histogram of correlation coefficients for all pairs of 40 cells from a. e, Probability distribution of synchronous spiking events in the 40 cell population in response to a long natural movie (red) approximates an exponential (dashed red). The distribution of synchronous events for the same 40 cells after shuffling each cell's spike train to eliminate all correlations (blue), compared to the Poisson distribution (dashed light blue). f, The rate of occurrence of each pattern predicted if all cells are independent is plotted against the measured rate. Each dot stands for one of the 210 = 1,024 possible binary activity patterns for 10 cells. Black line shows equality. Two examples of extreme mis-estimation of the actual pattern rate by the independent model are highlighted (see the text).
The small values of the correlation coefficients suggest an approximation in which the cells are completely independent. For most pairs, this is true with a precision of a few per cent, but if we extrapolate this approximation to the whole population of 40 cells, it fails disastrously. In Fig. 1e, we show the probability P(K) that K of these cells generate a spike in the same small window of duration Δτ. If the cells were independent, P(K) would approximate the Poisson distribution, whereas the true distribution is nearly exponential. For example, the probability of K = 10 spiking together is ∼105× larger than expected in the independent model.
The discrepancy between the independent model and the actual data is even more clear if we look at particular patterns of response across the population. Choosing N = 10 cells out of the 40, we can form an N-letter binary word to describe the instantaneous state of the network, as in Fig. 1b. The independent model makes simple predictions for the rate at which each such word should occur, and Fig. 1f shows these predictions as a scatter plot against the actual rate at which the words occur in the experiment. At one extreme, the word 1011001010 occurs once per minute, whereas the independent model predicts that this should occur once per three years (a discrepancy of ∼106×). Conversely, the word 1000000010 is predicted to occur once per three seconds, whereas in fact it occurred only three times in the course of an hour. The independent model makes order-of-magnitude errors even for very common patterns of activity, such as a single cell generating a spike while all others are silent. Moreover, within the clusters corresponding to different total numbers of spikes, the predictions and observations are strongly anti-correlated.
We conclude that weak correlations among pairs of neurons coexist with strong correlations in the states of the population as a whole. One possible explanation is that there are specific multi-neuron correlations, whether driven by the stimulus or intrinsic to the network, which simply are not measured by looking at pairs of cells. Searching for such higher-order effects presents many challenges22-24. Another scenario is that small correlations among very many pairs could add up to a strong effect on the network as a whole. If correct, this would be an enormous simplification in our description of the network dynamics.
Minimal consequences of pairwise correlations
To describe the network as a whole, we need to write down a probability distribution for the 2N binary words corresponding to patterns of spiking and silence in the population. The pairwise correlations tell us something about this distribution, but there are an infinite number of models that are consistent with a given set of pairwise correlations. The difficulty thus is to find a distribution that is consistent only with the measured correlations, and does not implicitly assume the existence of unmeasured higher-order interactions. As the entropy of a distribution measures the randomness or lack of interaction among different variables25, this minimally structured distribution that we are looking for is the maximum entropy distribution26 consistent with the measured properties of individual cells and cell pairs27.
We recall that maximum entropy models have a close connection to statistical mechanics: physical systems in thermal equilibrium are described by the Boltzmann distribution, which has the maximum possible entropy given the mean energy of the system26,28. Thus, any maximum entropy probability distribution defines an energy function for the system we are studying, and we will see that the energy function relevant for our problem is an Ising model. Ising models have been discussed extensively as models for neural networks29,30, but in these discussions the model arose from specific hypotheses about the network dynamics. Here, the Ising model is forced upon us as the least-structured model that is consistent with measured spike rates and pairwise correlations; we emphasize that this is not an analogy or a metaphor, but rather an exact mapping.
Whether we view the maximum entropy model through its analogy with statistical physics or simply as a model to be constructed numerically from the data (see Methods), we need meaningful ways of assessing whether this model is correct. Generally, for a network of N elements, we can define maximum entropy distributions PK that are consistent with all Kth-order correlations for any K = 1, 2, …, N (ref. 27). These distributions form a hierarchy, from K = 1 where all elements are independent, up to K = N, which is an exact description that allows arbitrarily complex interactions; their entropies SK decrease monotonically toward the true entropy S : S1 ≥ S2 ≥ … ≥ SN = S. The entropy difference or multi-information IN = S1 − SN measures the total amount of correlation in the network, independent of whether it arises from pairwise, triplet or more-complex correlations31. The contribution of the Kth-order correlation is I(K) = SK − 1 − Sk and is always positive (more correlation always reduces the entropy); IN is the sum of all the I(K) (ref. 27). Therefore, the question of whether pairwise correlations provide an effective description of the system becomes the question of whether the reduction in entropy that comes from these correlations, I(2) = S1 − S2, captures all or most of the multi-information IN.
Are pairwise correlations enough?
Figure 2 shows the predictions of the maximum entropy model P2 consistent with pairwise correlations in populations of N = 10 cells. Looking in detail at the patterns of spiking and silence of one group of 10 cells, we see that the predicted rates for different binary words are tightly correlated with the observed rates over a very large dynamic range, so that the dramatic failures of the independent model have been overcome (Fig. 2a).
Figure 2.
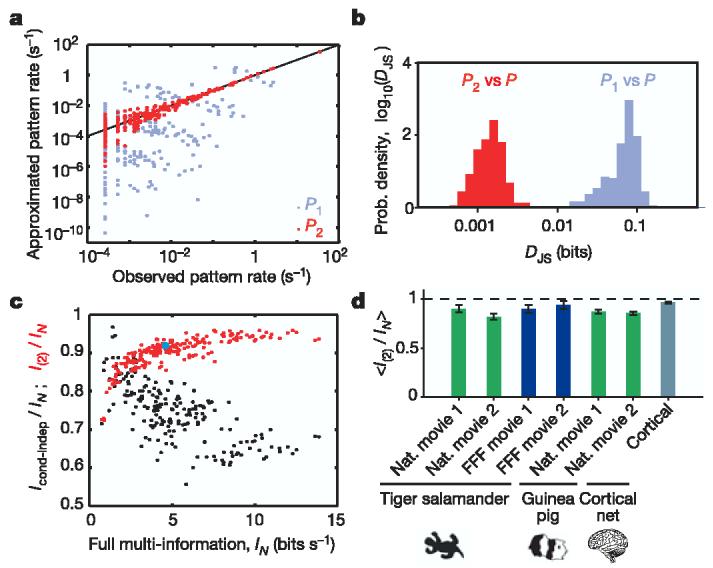
A maximum entropy model including all pairwise interactions gives an excellent approximation of the full network correlation structure. a, Using the same group of 10 cells from Fig. 1, the rate of occurrence of each firing pattern predicted from the maximum entropy model P2 that takes into account all pairwise correlations is plotted against the measured rate (red dots). The rates of commonly occurring patterns are predicted with better than 10% accuracy, and scatter between predictions and observations is confined largely to rare events for which the measurement of rates is itself uncertain. For comparison, the independent model P1 is also plotted (from Fig. 1f; grey dots). Black line shows equality. b, Histogram of Jensen–Shannon divergences (see Methods) between the actual probability distribution of activity patterns in 10-cell groups and the models P1 (grey) and P2 (red); data from 250 groups. c, Fraction of full network correlation in 10-cell groups that is captured by the maximum entropy model of second order, I(2)/IN, plotted as a function of the full network correlation, measured by the multi-information IN (red dots). The multi-information values are multiplied by 1/Δτ to give bin-independent units. Every dot stands for one group of 10 cells. The 10-cell group featured in a is shown as a light blue dot. For the same sets of 10 cells, the fraction of information of full network correlation that is captured by the conditional independence model, Icond–indep/IN, is shown in black (see the text). d, Average values of I(2)/IN from 250 groups of 10 cells. Results are shown for different movies (see Methods), for different species (see Methods), and for cultured cortical networks; error bars show standard errors of the mean. Similar results are obtained on changing N and Δτ; see Supplementary Information.
With 40 cells, we can choose many different populations of 10 cells, and in each case we find that the predicted and observed distributions of words are very similar. It would typically take thousands of independent samples to distinguish reliably between the true distribution of responses and the maximum entropy model, two orders of magnitude more than for the independent model (Fig. 2b).
The success of the pairwise maximum entropy models in capturing the correlation structure of the network is summarized by the fraction I(2)/IN ≈ 90% (Fig. 2c). This ratio is larger when IN itself is larger, so that the pairwise model is more effective in describing populations of cells with stronger correlations, and the ability of this model to capture ∼90% of the multi-information holds independent of many details (Fig. 2d; see also Supplementary Information): we can vary the particular natural movies shown to the retina, use an artificial movie, change the size of the bins Δτ used to define the binary responses, change the number of neurons N that we analyse, and even shift from a lower vertebrate (salamander) to a mammalian (guinea pig) retina. Finally, the correlation structure in a network of cultured cortical neurons32 can be captured by the pairwise model with similar accuracy.
The maximum entropy model describes the correlation structure of the network activity without assumptions about its mechanistic origin. A more traditional approach has been to dissect the correlations into contributions that are intrinsic to the network and those that are driven by the visual stimulus. The simplest model in this view is one in which cells spike independently in response to their input, so that all correlations are generated by covariations of the individual cells' firing rates33. Although there may be situations in which conditional independence is a good approximation, Fig. 2c shows that this model is less effective than the maximum entropy model in capturing the multi-information for 232 out of 250 groups of 10 neurons, even though the conditional independent model has ∼200 times more parameters (see Methods). The hypothesis of conditional independence is consistently less effective in capturing the structure of more-strongly correlated groups of cells, which is opposite to the behaviour of the maximum entropy model. Finally, whereas the maximum entropy model can be constructed solely from the observed correlations among neurons, the conditionally independent model requires explicit access to repeated presentations of the visual stimulus. Thus, the central nervous system could learn the maximum entropy model from the data provided by the retina alone, but the conditionally independent model is not biologically realistic in this sense.
We conclude that although the pairwise correlations are small and the multi-neuron deviations from independence are large, the maximum entropy model consistent with the pairwise correlations captures almost all of the structure in the distribution of responses from the full population of neurons. Thus, the weak pairwise correlations imply strongly correlated states. To understand how this happens, it is useful to look at the mathematical structure of the maximum entropy distribution.
Ising models, revisited
We recall that the maximum entropy distribution consistent with a known average energy 〈E〉 is the Boltzmann distribution, P ∝ exp(−E/kBT), where kB is Boltzmann's constant and T is temperature. This generalizes, so that if we know the average values of many variables fμ describing the system, then the maximum entropy distribution is P ∝ exp(−∑μλμfμ), where there is a separate Lagrange multiplier λμ for each constraint26,28. In our case, we are given the average probability of a spike in each cell and the correlations among all pairs. If we represent the activity of cell i by a variable σi = ±1, where + 1 stands for spiking and −1 stands for silence, then these constraints are equivalent to fixing the average of each σi and the averages of all products σiσj, respectively. The resulting maximum entropy distribution is
| (1) |
where the Lagrange multipliers {hi, Jij} have to be chosen so that the averages {〈σi〉, 〈σiσj〉} in this distribution agree with experiment; the partition function Z is a normalization factor. This is the Ising model28, where the σi are spins, the hi are local magnetic fields acting on each spin, and the Jij are the exchange interactions; note that h > 0 favours spiking and J > 0 favours positive correlations. Figure 3 shows the parameters {hi, Jij} for a particular group of ten cells, as well as the distributions of parameters for many such groups. Most cells have a negative local field, which biases them toward silence. Figure 3c and d illustrates the non-trivial relationship between the pairwise interaction strengths Jij and the observed pairwise correlations.
Figure 3.
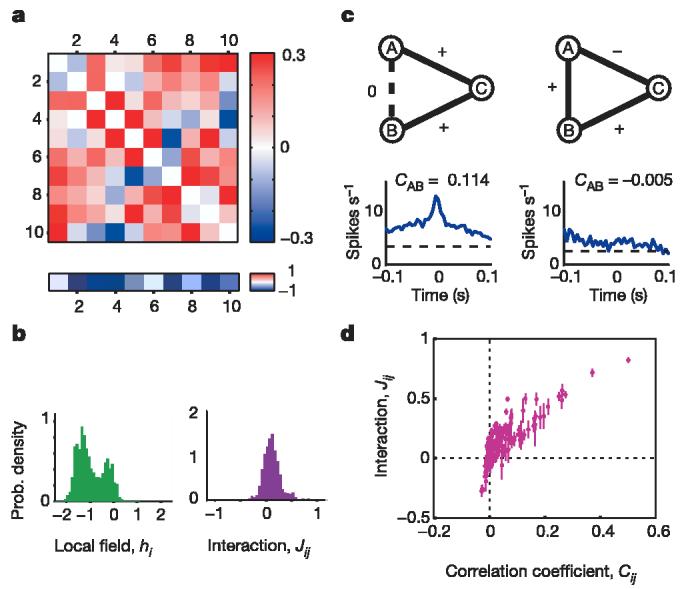
Pairwise interactions and individual cell biases, as in equation (1). a, Example of the pairwise interactions Jij (above) and bias values (or local fields) hi (below) for one group of 10 cells. b, Histograms of hi and Jij values from 250 different groups of 10 cells. c, Two examples of 3 cells within a group of 10. At left, cells A and B have almost no interaction (JAB = −0.02), but cell C is very strongly interacting with both A and B (JAC = 0.52, JBC = 0.70), so that cells A and B exhibit strong correlation, as shown by their cross-correlogram (bottom panel). At right, a ‘frustrated’ triplet, in which cells A and B have a significant positive interaction (JAB = 0.13), as do cells B and C (JBC = 0.09), but A and C have a significant negative interaction (JAC = −0.11). As a result, there is no clear correlation between cells A and B, as shown by their cross-correlogram (bottom panel). d, Interaction strength Jij plotted against the correlation coefficient Cij; each point shows the value for one cell pair averaged over many different groups of neighbouring cells (190 pairs from 250 groups), and error bars show standard deviations.
We can rewrite equation (1) exactly by saying that each neuron or spin σi experiences an effective magnetic field that includes the local field or intrinsic bias hi and a contribution from interactions with all the other spins (neurons), ; note that depends on whether the other cells are spiking or silent. The intrinsic bias dominates in small groups of cells, but as we look to larger networks, the fact that almost all of the ∼N2 pairs of cells are significantly (if weakly) interacting shifts the balance so that the typical values of the intrinsic bias are reduced while the effective field contributed by the other cells has increased (Fig. 4).
Figure 4.
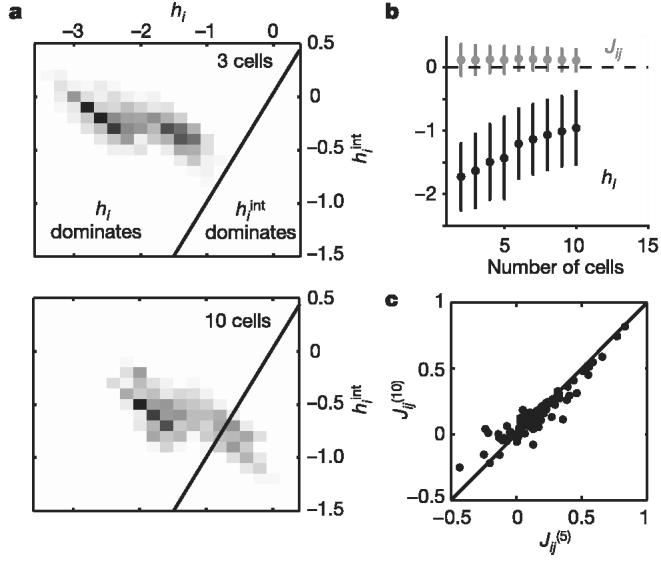
Interactions and local fields in networks of different size. a, Greyscale density map of the distribution of effective interaction fields experienced by a single cell versus its own bias or local field hi (see the text); distribution formed over network configurations at each point in time during a natural movie for n = 1,140 3-cell groups (top panel) and n = 250 10-cell groups (bottom panel). Black line shows the boundary between dominance of local fields versus interactions. b, Mean interactions Jij and local fields hi describing groups of N cells, with error bars showing standard deviations across multiple groups. c, Pairwise interaction in a network of 10 cells plotted against the interaction values of the same pair in a sub-network containing only 5 cells . Line shows equality.
Larger networks and error correction
Groups of N = 10 cells are large enough to reveal dramatic departures from independence, but small enough that we can directly sample the relevant probability distributions. What happens at larger N? In general, we expect that the total capacity of the network to represent its sensory inputs should grow in proportion to the number of neurons, N. This is the usual thermodynamic limit in statistical mechanics, where energy and entropy are proportional to system size28. But this behaviour is not guaranteed when all elements of the system interact with each other. In the Ising model, it is known that if all pairs of spins (here, cells) interact significantly, then to recover the thermodynamic limit the typical size of the interactions Jij must decrease with N (refs 30, 34). Although we have not analysed very large networks, we see no signs of significant changes in J with growing N (Fig. 4b, c).
In a physical system, the maximum entropy distribution is the Boltzmann distribution, and the behaviour of the system depends on the temperature, T. For the network of neurons, there is no real temperature, but the statistical mechanics of the Ising model predicts that when all pairs of elements interact, increasing the number of elements while fixing the typical strength of interactions is equivalent to lowering the temperature, T, in a physical system of fixed size, N. This mapping predicts that correlations will be even more important in larger groups of neurons.
We can see signs of strong correlation emerging by looking at the entropy and multi-information in sub-networks of different sizes. If all cells were independent, the entropy would be S1, exactly proportional to N. For weak correlations, we can solve the Ising model in perturbation theory to show that the multi-information IN is the sum of mutual information terms between all pairs of cells, and hence IN ∝ N(N − 1). This is in agreement with the empirically estimated IN up to N = 15, the largest value for which direct sampling of the data provides a good estimate (Fig. 5a), and Monte Carlo simulations of the maximum entropy models suggest that this agreement extends up to the full population of N = 40 neurons in our experiment (G. Tkačik, E.S., R.S., M.J.B. and W.B., unpublished data). Were this pattern to continue, at N ≈ 200 cells IN would become equal to the independent entropy S1, and the true entropy SN = S1 – IN would vanish as the system ‘froze’. Because we see variable firing patterns of all the cells, we know that literal freezing of the network into a single state doesn't happen. On the other hand, networks of N ≈ 200 cells must be very strongly ordered. Interestingly, experiments indicate that a correlated patch on the retina has roughly this size: the strongest correlations are found for cells within ∼200 μm of each other, and this area contains ∼175 ganglion cells in the salamander19.
Figure 5.
Extrapolation to larger networks. a, Average independent cell entropy S1 and network multi-information IN, multiplied by 1/Δτ to give bin-independent rates, versus number of cells in the network N. Theoretically, we expect IN ∝ N(N − 1) for small N; the best fit is IN ∝ N1.98±0.04. Extrapolating (dashed line) defines a critical network size Nc, where IN would be equal to S1. b, Information that N cells provide about the activity of cell N + 1, plotted as a fraction of that cell's entropy, S(σi), versus network size N; each point is the average value for many different groups of cells. Extrapolation to larger networks (dashed line, slope = 1.017 ± 0.052) defines another critical network size Nc, where one would get perfect error-correction or prediction of the state of a single cell from the activity of the rest of the network. c, Examples of ‘check cells’, for which the probability of spiking is an almost perfectly linear encoding of the number of spikes generated by the other cells in the network. Cell numbers as in Fig. 1.
Because the interactions Jij have different signs, frustration (Fig. 3c) can prevent the freezing of the system into a single state. Instead there will be multiple states that are local minima of the effective energy function, as in spin glasses34. We find that roughly 40% of all triplets of cells are indeed frustrated. If the number of minimum energy patterns is not too small, then the system retains a significant representational capacity. If the number of patterns is not too large, then observing only some of the cells in the network is sufficient to identify the whole pattern uniquely, just as in the Hopfield model of associative memory29. Thus, the system would have a holographic or error-correcting property, so that an observer who has access only to a fraction of the neurons would nonetheless be able to reconstruct the activity of the whole population.
We can see suggestions of this error-correcting property by asking directly how much the knowledge of activity in N cells tells us about whether cell N + 1 will spike (Fig. 5b). Our uncertainty about the state of one cell is reduced in proportion to the number of cells that we examine, and if this trend continues, then again at N ≈ 200 all uncertainty would vanish. Alternatively, we can look for particular kinds of error correction. In our population of 40 cells, we have found three cells for which the probability of spiking is an almost perfectly linear encoding of the number of spikes generated by the other cells in the network (Fig. 5c). To the extent that local field potentials or intrinsic optical signals in cortex reflect the total number of spikes generated by nearby neurons, this observation is analogous to the statement that the spiking in single pyramidal cells is correlated with these more collective responses35. By observing the activity of the ‘check cells’ in Fig. 5c, we can estimate how many spikes are generated by the network as a whole even before we observe any of the other cells' responses.
Discussion
We have seen that the maximum entropy principle provides a unique candidate model for the whole network that is consistent with observations on pairs of elements but makes no additional assumptions. Despite the opportunity for higher-order interactions in the retina, this model captures more than 90% of the structure in the detailed patterns of spikes and silence in the network, closing the enormous gap between the data and the predictions of a model in which cells fire independently. Because the maximum entropy model has relatively few parameters, we evade the curse of dimensionality and associated sampling problems that would ordinarily limit the exploration of larger networks. The low spiking probabilities, and weak but significant correlations among almost all pairs of cells, are not unique to the retina. Indeed, the maximum entropy model of second order captures over 95% of the multi-information in experiments on cultured networks of cortical neurons. In addition, application of the maximum entropy formalism of ref. 27 to ganglion cells in monkey retina shows that pairwise correlations in groups of up to N = 8 ‘ON’ or ‘OFF’ parasol cells, restricted to adjacent cells in each mosaic, can account for 98% of the observed deviations from statistical independence (E. J. Chichilnisky, personal communication).
The success of a model that includes only pairwise interactions provides an enormous simplification in our description of the network. This may be important not only for our analysis, but also for the brain. The dominance of pairwise interactions means that learning rules based on pairwise correlations36 could be sufficient to generate nearly optimal internal models for the distribution of ‘codewords’ in the retinal vocabulary, thus allowing the brain to accurately evaluate new events for their degree of surprise37.
The mapping of the maximum entropy problem to the Ising model, together with the observed level of correlations, implies that groups of N ≈ 200 cells will behave very differently than smaller groups, and this is especially interesting because the patch of significantly correlated ganglion cells in the retina is close to this critical size19. Because the response properties of retinal ganglion cells adapt to the input image statistics38,39, this matching of correlation length and correlation strength cannot be an accident of anatomy but rather must be set by adaptive mechanisms. Perhaps there is an optimization principle that determines this operating point, maximizing coding capacity while maintaining the correlation structures that enable error-correction.
Although we have focused on networks of neurons, the same framework has the potential to describe biological networks more generally. In this view, the network is much more than the sum of its parts, but a nearly complete model can be derived from all its pairs.
METHODS
Retinal experiments
Retinae from the larval tiger salamander (Ambystoma tigrinum) and the guinea pig (Cavia porcellus) were isolated from the eye, retaining the pigment epithelium, and placed over a multi-electrode array19. Both were perfused with oxygenated medium: room temperature Ringers for salamander and 36 °C Ames medium for guinea pig. Extracellular voltages were recorded by a MultiChannel Systems MEA 60 microelectrode array and streamed to disk for offline analysis. Spike waveforms were sorted either using the spike size and shape from a single electrode19 or the full waveform on 30 electrodes18. Recorded ganglion cells were spaced no more than 500 μm apart, and were typically close enough together to have overlapping receptive field centres. Our analysis is based on measurements of 95 cells recorded in 4 salamanders and 35 cells recorded in 2 guinea pigs.
Natural movie clips (‘Nat.’ in Fig. 2) were acquired using a Canon Optura Pi video camera at 30 frames per second. Movie clips broadly sampled woodland scenes as well as man-made environments, and included several qualitatively different kinds of motion: objects moving in a scene, optic flow, and simulated saccades19. In spatially uniform flicker (‘FFF’ in Fig. 2), the light intensity was randomly chosen to be black or white every 16.7 ms. For most experiments, a 20–30 s stimulus segment was repeated many times; in one experiment, a 16 min movie clip was repeated several times. All visual stimuli were displayed on an NEC FP1370 monitor and projected onto the retina using standard optics. The mean light level was 5 lux, corresponding to photopic vision.
Cultured cortical networks
Data on cultured cortical neurons were recorded by the laboratory of S. Marom (Technion–Israel Institute of Technology) using a multi-electrode array, as described in ref. 32. The data set analysed here is an hour-long epoch of spontaneous neuronal activity recorded through 60 electrodes.
Analysis
Mean spike rates ranged from 0.3 to 4.5 spikes s−1. Spike trains are binned using Δτ = 20-ms windows (unless otherwise noted) into binary sequences of spiking (1) and non-spiking (0); in the rare cases where there is more than one spike in a bin, we denote it as ‘1’. Cross-correlation values were estimated by discretizing the neural response into binary (spike/no spike) variables for each cell, using Δτ = 20-ms bins, and then computing the correlation coefficients among these variables. Because the data sets we consider here are very large (∼1 hour), the threshold for statistical significance of the individual correlation coefficients is well below |C| 0.01.
Information theoretic quantities such as IN depend on the full distribution of states for the real system. Estimating these quantities can be difficult, because finite data sets lead to systematic errors40. With large data sets (∼1 hour) and N < 15 cells, however, systematic errors are small, and we can use the samplesize dependence of the estimates to correct for these errors, as in ref. 41. For networks of modest size, as considered here, constructing the maximum entropy distribution consistent with the mean spike rates and pairwise correlations can be viewed as an optimization problem with constraints. Because the entropy is a convex function of the probabilities, and the constraints are linear, many efficient algorithms are available42. To test our models we sometimes need surrogate data without correlations. To remove all correlations among neurons (Fig. 1), we shift the whole spike train of each cell by a random time relative to all the other cells. To generate the conditionally independent responses (Fig. 2), we use data from repeated presentations (trials) of the same movie and shuffle the trial labels on each cell independently. We then use the joint probability distribution of the cells under conditional independence, Pcond-indep(σ1, σ2,…, σN), to compute Icond-indep = S1 – S[Pcond-indep(σ1, σ2,…, σN)]. Note that the conditionally independent model has NT/Δτ parameters, because each cell has its own spike rate, potentially different at each moment in time, where T is the duration of the stimulus movie; in our case NT/Δτ ≈ 104, in contrast to the N(N 1)/2 = 55 parameters of the maximum entropy model, for N = 10 cells.
The Jensen–Shannon divergence, DJS [p∥q], quantifies the dissimilarity of the distributions p and q, essentially measuring the inverse of the number of independent samples we would need in order to be sure that the two distributions were different43.
Acknowledgements
We thank G. Stephens and G. Tkačik for discussions, N. Tkachuk for help with the experiments, S. Marom for sharing his lab's cultured cortical networks data with us, and E. J. Chichilnisky for sharing his lab's primate retina results with us. This work was supported in part by the NIH and by the E. Matilda Zeigler Foundation.
Footnotes
Supplementary Information is linked to the online version of the paper at www.nature.com/nature.
References
- 1.Hopfield JJ, Tank DW. Computing with neural circuits: a model. Science. 1986;233:625–633. doi: 10.1126/science.3755256. [DOI] [PubMed] [Google Scholar]
- 2.Georgopoulos AP, Schwartz AB, Kettner RE. Neuronal population coding of movement direction. Science. 1986;233:1416–1419. doi: 10.1126/science.3749885. [DOI] [PubMed] [Google Scholar]
- 3.Hartwell LH, Hopfield JJ, Leibler S, Murray AW. From molecular to modular cell biology. Nature. 1999;402(Suppl C):47–52. doi: 10.1038/35011540. [DOI] [PubMed] [Google Scholar]
- 4.Barabási A-L, Oltvai ZN. Network biology: Understanding the cell's functional organization. Nature Rev. Genet. 2004;5:101–113. doi: 10.1038/nrg1272. [DOI] [PubMed] [Google Scholar]
- 5.Perkel DH, Bullock TH. Neural coding. Neurosci. Res. Prog. Sum. 1968;3:221–348. [Google Scholar]
- 6.Zohary E, Shadlen MN, Newsome WT. Correlated neuronal discharge rate and its implications for psychophysical performance. Nature. 1994;370:140–143. doi: 10.1038/370140a0. [DOI] [PubMed] [Google Scholar]
- 7.Meister M, Lagnado L, Baylor DA. Concerted signaling by retinal ganglion cells. Science. 1995;270:1207–1210. doi: 10.1126/science.270.5239.1207. [DOI] [PubMed] [Google Scholar]
- 8.Riehle A, Grun S, Diesmann M, Aertsen A. Spike synchronization and rate modulation differentially involved in motor cortical function. Science. 1997;278:1950–1953. doi: 10.1126/science.278.5345.1950. [DOI] [PubMed] [Google Scholar]
- 9.Dan Y, Alonso JM, Usrey WM, Reid RC. Coding of visual information by precisely correlated spikes in the lateral geniculate nucleus. Nature Neurosci. 1998;1:501–507. doi: 10.1038/2217. [DOI] [PubMed] [Google Scholar]
- 10.Hatsopoulos N, Ojakangas C, Paninski L, Donoghue J. Information about movement direction obtained from synchronous activity of motor cortical neurons. Proc. Natl Acad. Sci. USA. 1998;95:15706–15711. doi: 10.1073/pnas.95.26.15706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Abbott LF, Dayan P. The effect of correlated variability on the accuracy of a population code. Neural Comput. 1999;11 doi: 10.1162/089976699300016827. [DOI] [PubMed] [Google Scholar]
- 12.Bair W, Zohary E, Newsome WT. Correlated firing in macaque visual area MT: time scales and relationship to behavior. J. Neurosci. 2001;21:1676–1697. doi: 10.1523/JNEUROSCI.21-05-01676.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shamir M, Sompolinsky H. Nonlinear population codes. Neural Comput. 2004;16:1105–1136. doi: 10.1162/089976604773717559. [DOI] [PubMed] [Google Scholar]
- 14.Eisen MB, Spellman PT, Brown PO, Botstein D. Cluster analysis and display of genome-wide expression patterns. Proc. Natl Acad. Sci. USA. 1998;95:14863–14868. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Alter O, Brown PO, Botstein D. Singular value decomposition for genome-wide expression data processing and modeling. Proc. Natl Acad. Sci. USA. 2000;97 doi: 10.1073/pnas.97.18.10101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Holter NS, Maritan A, Cieplak M, Federoff NV, Banavar JR. Dynamic modeling of gene expression data. Proc. Natl Acad. Sci. USA. 2001;98:1693–1698. doi: 10.1073/pnas.98.4.1693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Meister M, Pine J, Baylor DA. Multi-neuronal signals from the retina: acquisition and analysis. J. Neurosci. Methods. 1994;51:95–106. doi: 10.1016/0165-0270(94)90030-2. [DOI] [PubMed] [Google Scholar]
- 18.Segev R, Goodhouse J, Puchalla JL, Berry MJ., II Recoding spikes from a large fraction of the ganglion cells in a retinal patch. Nature Neurosci. 2004;7:1155–1162. doi: 10.1038/nn1323. [DOI] [PubMed] [Google Scholar]
- 19.Puchalla JL, Schneidman E, Harris RA, Berry MJ., II Redundancy in the population code of the retina. Neuron. 2005;46:492–504. doi: 10.1016/j.neuron.2005.03.026. [DOI] [PubMed] [Google Scholar]
- 20.Frechette ES, et al. Fidelity of the ensemble code for visual motion in primate retina. J. Neurophysiol. 2005;94:119–135. doi: 10.1152/jn.01175.2004. [DOI] [PubMed] [Google Scholar]
- 21.Rieke F, Warland D, de Ruyter van Steveninck R, Bialek W. Spikes: Exploring the Neural Code. MIT Press; Cambridge: 1997. [Google Scholar]
- 22.Martignon L, et al. Neural coding: higher-order temporal patterns in the neurostatistics of cell assemblies. Neural Comput. 2000;12:2621–2653. doi: 10.1162/089976600300014872. [DOI] [PubMed] [Google Scholar]
- 23.Grun S, Diesmann M, Aertsen A. Unitary events in multiple single-neuron spiking activity: I. Detection and significance. Neural Comput. 2002;14:43–80. doi: 10.1162/089976602753284455. [DOI] [PubMed] [Google Scholar]
- 24.Schnitzer MJ, Meister M. Multineuronal firing patterns in the signal from eye to brain. Neuron. 2003;37:499–511. doi: 10.1016/s0896-6273(03)00004-7. [DOI] [PubMed] [Google Scholar]
- 25.Brillouin L. Science and Information Theory. Academic; New York: 1962. [Google Scholar]
- 26.Jaynes ET. Information theory and statistical mechanics. Phys. Rev. 1957;106:62–79. [Google Scholar]
- 27.Schneidman E, Still S, Berry MJ, II, Bialek W. Network information and connected correlations. Phys. Rev. Lett. 2003;91:238701. doi: 10.1103/PhysRevLett.91.238701. [DOI] [PubMed] [Google Scholar]
- 28.Landau LD, Lifshitz EM. Statistical Physics. 3rd edn Pergamon; Oxford: 1980. [Google Scholar]
- 29.Hopfield JJ. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl Acad. Sci. USA. 1982;79:2554–2558. doi: 10.1073/pnas.79.8.2554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Amit DJ. Modeling Brain Function: The World of Attractor Neural Networks. Cambridge Univ. Press; Cambridge, UK: 1989. [Google Scholar]
- 31.Cover TM, Thomas JA. Elements of Information Theory. Wiley & Sons; New York: 1991. [Google Scholar]
- 32.Eytan D, Brenner N, Marom S. Selective adaptation in networks of cortical neurons. J. Neurosci. 2003;23:9349–9356. doi: 10.1523/JNEUROSCI.23-28-09349.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Perkel DH, Gerstein GL, Moore GP. Neuronal spike trains and stochastic point processes. II. Simultaneous spike trains. Biophys. J. 1967;7:419–440. doi: 10.1016/S0006-3495(67)86597-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mezard M, Parisi G, Virasoro MA. Spin Glass Theory and Beyond. World Scientific; Singapore: 1987. [Google Scholar]
- 35.Arieli A, Sterkin A, Grinvald A, Aertsen A. Dynamics of ongoing activity: explanation of the large variability in evoked cortical responses. Science. 1996;273:1868–1871. doi: 10.1126/science.273.5283.1868. [DOI] [PubMed] [Google Scholar]
- 36.Bi G, Poo MM. Synaptic modification by correlated activity: Hebb's postulate revisited. Annu. Rev. Neurosci. 2001;24:139–166. doi: 10.1146/annurev.neuro.24.1.139. [DOI] [PubMed] [Google Scholar]
- 37.Barlow H. Conditions for versatile learning, Helmholtz's unconscious inference, and the task of perception. Vision Res. 1990;30:1561–1571. doi: 10.1016/0042-6989(90)90144-a. [DOI] [PubMed] [Google Scholar]
- 38.Smirnakis S, Berry MJ, II, Warland DK, Bialek W, Meister M. Adaptation of retinal processing to image contrast and spatial scale. Nature. 1997;386:69–73. doi: 10.1038/386069a0. [DOI] [PubMed] [Google Scholar]
- 39.Hosoya T, Baccus SA, Meister M. Dynamic predictive coding by the retina. Nature. 2005;436:71–77. doi: 10.1038/nature03689. [DOI] [PubMed] [Google Scholar]
- 40.NIPS 2003 Workshop http://nips.cc/Conferences/2003/Workshops/EstimationofEntropy Estimation of entropy and information of undersampled probability distributions. 2003
- 41.Strong SP, Koberle iR., de Ruyter van Steveninck RR, Bialek W. Entropy and information in neural spike trains. Phys. Rev. Lett. 1998;80:197–200. [Google Scholar]
- 42.Darroch JN, Ratcliff D. Generalized iterative scaling for log–linear models. Ann. Math. Stat. 1972;43:1470–1480. [Google Scholar]
- 43.Lin J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory. 1991;37:145–151. [Google Scholar]




